Моделирование перелёта межорбитального буксира с солнечной электроракетной двигательной установкой

Задача создания эффективных космических транспортных систем является одним из приоритетных направлений реализации проектов по исследованию и освоению околоземного космического пространства и Солнечной системы, включая выведение телекоммуникационных и навигационных систем на высокие околоземные орбиты [1–3].

Возможным направлением решения этой задачи является создание эффективных космических буксиров с энергодвигательными установками на основе электроракетных двигателей (ЭРД), обеспечивающих реализацию транспортных операций с минимальными затратами рабочего тела (РТ). Использование маршевой электроракетной двигательной установки (ЭРДУ) благодаря значительно большему удельному импульсу позволяет существенно уменьшить массовые затраты на межорбитальные перелёты и добиться увеличения доли полезной нагрузки в стартовой массе космических аппаратов (КА). В настоящее время рассматриваются варианты транспортных систем с ЭРДУ, использующими для своего электроснабжения солнечные (СЭУ) [1–6] и ядерные энергоустановки (ЯЭУ) [7]. Однако основное направление этих исследований касается, главным образом, разработки конструкционного облика аппаратов, а также выбора и оптимизации траекторий для полёта на геостационарную орбиту, к Луне и для межпланетных полётов.

В данной работе рассмотрена простейшая транспортная задача доставки полезной нагрузки с помощью межорбитального буксира (МБ), оснащённого солнечной электроракетной двигательной установкой (СЭРДУ), с опорной орбиты (ОО) высотой 300 км на компланарную рабочую орбиту (РО) высотой 20 000 км. Основное внимание уделено влиянию различного состава энергосистемы буксира и режимов её работы на параметры перелётов. Рассмотрены варианты комплектации энергосистемы из солнечных батарей (СБ), работающих совместно с аккумуляторными (АБ) для электропитания ЭРДУ на теневых участках траектории полёта, и без АБ.

В первом разделе статьи выполняются приближённые оценки энергозатрат на перелёт с учётом указанных параметров, и на их основе определяются близкие к оптимальным проектные параметры буксира. Далее на основе численного интегрирования уравнений движения МБ подробно исследуется баллистика перелёта, включая возвращение на ОО.

Моделируется режим двухстепенной ориентации СБ в направлении на Солнце и учитывается температура панелей СБ на основе уравнений теплового баланса при определении аэродинамического сопротивления. Для упрощения задачи принимается простейшая конструкция буксира, включающая только основные элементы энергодвигательной системы.

общая характеристика задачи полёта МБ с СЭрду

Полёт МБ с СЭРДУ имеет несколько отличительных признаков, отражающих специфику двигательной установки такого типа [8–11]. Особенно следует отметить важные, но малоизученные факторы, сопровождающие полёт в ближнем космосе:

• •    необходимость учёта реального поля тяготения Земли, вызывающего долгопериодические возмущения траектории полёта КА;

• •    аэродинамическое сопротивление верхней атмосферы Земли (выше 120 км), особенно значимое для КА, оснащённых СЭУ для электропитания ЭРДУ.

Как известно [12], значение оптимального удельного импульса ЭРДУ существенно зависит от характеристической скорости транспортной операции V_х . Основной причиной возникающей трудности является сложность простого учёта сил аэродинамического сопротивления и влияние нецентральности гравитационного поля.

В общем случае межорбитальный перелёт может подразумевать изменение высоты и наклонения орбиты КА. Изменение наклонения орбиты требует формирования компоненты вектора тяги перпендикулярно мгновенной плоскости траектории в направлении изменения плоскости орбиты (нормальная компонента тяги). В этом общем случае задача расчёта транспортной операции ещё более усложняется в связи с необходимостью выбора оптимальной программы управления полётом КА. Поэтому далее рассматривается межорбитальный перелёт с постоянным направлением вектора тяги ЭРДУ по вектору скорости КА. Такой перелёт близок к компланарному и наиболее прост в моделировании.

Решение задачи перелёта межорбитального буксира с СЭРДУ включает в себя:

• •    моделирование конструкции буксира;

• • построение баллистической модели полёта буксира с СЭРДУ.

расчётная модель буксира с солнечной энергоустановкой

Режимы работы энергосистемы МБ с СЭРДУ. Для поддержания непрерывного энергоснабжения бортовых потребителей на теневой стороне, в т. ч. и для электропитания ЭРДУ, в состав энергосистемы буксира можно включить АБ. В наиболее простом случае энергосистема буксира, оснащённого СЭУ и АБ, функционирует в следующих режимах:

а. Буксир освещается Солнцем:

а1. Энергия от СБ расходуется на электропитание ЭРДУ мощностью Р _ЭРДУ .

а2. Энергия от СБ расходуется на электропитание технических систем буксира мощностью Р _ТС .

а3. Энергия от СБ расходуется на зарядку АБ мощностью Р _ЭРДУ для электропитания ЭРДУ на теневом участке.

а4. Энергия от СБ расходуется на зарядку АБ мощностью Р _ТС для электропитания технических систем буксира на теневом участке.

После достижения заданного уровня энергетической ёмкости АБ Е _АБ0 зарядка отключается.

Б. Буксир в тени Земли:

Б1. Энергия от АБ расходуется на электропитание технических систем буксира Р _ТС .

Б2. Энергия от АБ расходуется на электропитание ЭРДУ мощностью Р _ЭРДУ .

При отсутствии АБ для энергоснабжения ЭРДУ пункты а3 и Б2 исключаются. На теневом участке орбиты работа ЭРДУ прекращается, и буксир совершает инерциальный полёт по оскулирующей орбите, рассчитанной по фазовым координатам точки останова работы ЭРДУ, до выхода на освещённый участок.

Энергетическая модель МБ с СЭРДУ. Основным потребителем электроэнергии, вырабатываемой СЭУ, является ЭРДУ, включающая n _ЭРД двигателей с заданными тягово-энергетическими характеристиками: тягой F _ЭРД , удельным импульсом I _ЭРД и КПД η _ЭРД . Соответственно, электрическая мощность ЭРД составит

ЭРД ЭРД .       ЭРД

,

Э РД                     ^m ЭРД

ηЭРД           ηЭРД где m. ЭРД — массовый расход РТ ЭРД.

В качестве РТ ЭРД далее рассматривается ксенон (Хе). Полная мощность ЭРДУ составит

Р = п Р

ЭРДУ   ⁿ ЭРД ЭРД

РТ ЭРД

^Т ДУ ^{2 η} ЭРД

где M _РТ — запас массы РТ для работы ЭРДУ в течение времени работы двигательной установки Т _ДУ при выполнении транспортной операции.

Наличие теневого участка траектории полёта буксира с СЭРДУ существенно усложняет расчётную модель буксира. Наибольшая продолжительность полёта в тени будет на участке, когда направление Земля – Солнце лежит в плоскости траектории или близкой к ней. В этом случае предельные оценки энергопотребления при полёте буксира на теневом участке можно определить из следующих соображений:

• •    угол теневой части орбиты (траектории) буксира

^R З

ϕ _т = 2 arcsin _R ^,                           (3)

п где RЗ — радиус Земли; Rп — радиус перигея;

• •    время полёта буксира в тени Земли

  Т = т

  
  

ϕ _т R _п

, V

п

где V _п — скорость буксира в перигее;

• •    энергозатраты на работу ЭРДУ в тени Земли на начальных витках

полёта и электропитание бортовых систем буксира, определяющие ёмкость АБ, равны

Е _АБ0 = ( Р _ЭРДУ + Р _ТС ) Т _т =

^М СБ ^{= ρ} СБ ^S СБ ^{=      Р} СБ

^η СБ ^Е С

= n ЭРД P ЭРД Т т + P ТС Т т ;                   (5)

• • часть мощности, генерируемой СБ, отводимая на зарядку АБ:

Е

АБ0 _{,                               (6)}

АБ Т – Т орб т где Торб — период орбиты МБ;

• • проектная мощность СБ с учётом выражения (5)

^Р СБ ^{= Р} ЭРДУ ^{+ Р} АБ ^{+ Р} ТС ⁼

=(1 + τ _т )( Р _ЭРДУ + Р _ТС ) =

= (1 + τ _т ) n _ЭРД P _ЭРД + (1 + τ _т ) Р _ТС ,         (7)

где τ т = Т т /( Т орб – Т т ).

При выполнении расчёта по формулам (3)–(7) возникает существенная неопределённость в оценках требуемой мощности СБ, обусловленная незнанием действительного положения теневых участков траектории полёта КА. Длительность этих участков в большой степени зависит от выбранной траектории, времени выполнения транспортной операции, параметров энергетической установки и двигательной системы.

Массовая модель МБ. Расчёт массы МБ выполняется от значения конечной массы МБ М _{КА р} , доставляемой на РО, которую можно определить следующим выражением

М КА р = М ПН + М СБ + М АБ +

+ М СЭС + М ЭРДУ + М СХП + М к , (8) где М _ПН — масса полезной нагрузки; М _СБ — масса СБ; М _АБ — масса АБ; М _СЭС — масса системы электроснабжения (СЭС), включающая систему преобразования тока [13]; М _ЭРДУ — масса ЭРДУ; М _СХП — масса системы хранения и подачи РТ (без РТ); М _к — масса конструкции МБ.

Масса СБ связана с её площадью S _СБ и КПД η _СБ :

^S СБ

р

СБ

^η СБ ^Е С

1 + τ              1 + τ т                                т, nЭРД ЭРД           ТС

^η СБ ^Е С            ^η СБ С

1 + τ т

^{= ρ} СБ        ⁿ

^η СБ ^Е С

1 + τ т _, ЭРД ЭРД ^ρ СБ         ТС

^η СБ ^Е С

где ρ _СБ — удельная масса СБ, кг/м².

Значение удельной массы СБ включает в себя соответствующую характеристику собственно фотоэлектронного преобразователя (ФЭП), защитного стекла, обычно изготовляемого из плавленого кварца, клеевого слоя и подложки [14–16]. В качестве подложки для СБ большой мощности целесообразно применять сотовые панели, придающие повышенную жёсткость батарее и обладающие приемлемой удельной массой. Перелёт межорбитального КА с низкой ОО на РО высотой несколько тысяч километров и более связан с длительным нахождением в радиационных поясах, вызывающих деградацию ФЭП. Для компенсации негативного влияния радиационных поясов рекомендуется увеличивать толщину защитного стекла, наклеиваемого на освещаемую поверхность ФЭП, а для защиты тыльной стороны ФЭП — увеличивать толщину сотовой панели. Анализ результатов, представленных в работах [14–16], и выполненные оценки дают основание определить величину ρ _СБ в диапазоне 3,5…4,5 кг/м².

Масса АБ зависит от её ёмкости

АБ0 т

М =     =    ( Р   + Р ) =

АБ                  ЭРДУ ТС

АБ ^w АБ

1 + τ                 1 + τ

= Т ^т n P + Т ^т P ^,       (11)

т          ЭРД ЭРД т          ТС wАБ              wАБ где wАБ — удельная энергоёмкость АБ, Дж/кг (принято для литий-ионных аккумуляторов с kАБ = 5,544·105 Дж/кг [15]);

Массу СЭС целесообразно соотнести с проектной мощностью СБ по формуле

M _СЭС = μ _СЭС Р _СБ = μ _СЭС (1 + τ _т ) ×

× n _ЭРД P _ЭРД + μ _СЭС (1 + τ _т ) Р _ТС ,           (12)

где μ _СЭС — коэффициент массы СЭС.

Массу ЭРДУ можно определить соотношением, связывающим количество ЭРД с их массой, функционально связанной с мощностью одного двигателя:

где Е _С = 1 380 Вт/м² — Солнечная постоянная;

χ

ЭРДУ nЭРД μЭРД Э РД, где μЭРД — коэффициент массы ЭРД; χ — показатель влияния мощности ЭРД на массу двигателя. Так, например, по данным источника [17] можно принять следующие оценки коэффициентов в этой формуле: μЭРД = 1,9 кг/(кВт)χ; χ = 0,75.

Для дальнейшего применения эту формулу целесообразно преобразовать, заменив количество двигателей отношением полного расхода РТ к расходу через один ЭРД m ^. _ЭРД :

M

РТ _χ

ЭРДУ ^µ ЭРД      ^. ЭРД

ДУ ^m ЭРД

M РТ    1	1 + χ ЭРД	(13)
= µ ЭРД T ДУ (2 η ЭРД ) χ	1 – χ ЭРД

Определим массу энергодвигательной системы (ЭДС) МБ:

M ЭДС = M СБ + M АБ + M СЭС + M ЭРДУ =

= ( μ _ЭДС Р

ЭРД

χ

^μ ЭРД ЭРД ⁿ ЭРД   ^μ ЭДС ТС^,

где

1 + τ _т 1 + τ _т

µ = ρ         + T + µ (1 + τ ) =

ЭДС СБ η _Е т w       СЭС      т

СБ С          АБ

^{ρ СБ} η _СБ Е _С

+

T

т

w _АБ

+ µ _СЭС

(1 + τ _т ),

слагаемые

которой непосредственно зависят от мощности ЭРД.

В данной работе принята газобаллонная система хранения и подачи рабочего тела (СХП) на основе унифицированных сферических баллонов высокого давления (БВД) комбинированной конструкции с композитной оболочкой

и металлическим лейнером производства ЗАКБ «САФИТ», лицензированных для авиационной и космической отрасли [18]. На основе этих данных в расчёты заложен сферический БВД объёмом V _БВД = 25 дм³, массой M _БВД = 6,2 кг с давлением РТ p _РТ ≤ 340 атм.

Масса РТ, содержащаяся в одном баллоне, по уравнению состояния идеального газа выражается формулой:

µ p

MРТ 1 = РТ Р Т V БВД, (15) РТ где μРТ — молекулярная масса РТ; pРТ, TРТ — давление и температура РТ соответственно; R — универсальная газовая постоянная.

В частности, масса ксенона в одном БВД при p _РТ = 340 атм и T _РТ = 300 К равна M _{РТ 1} = 44,6 кг. Фактически расчёт запаса РТ на транспортную операцию сводится к определению количества БВД в СХП n _БВД . Масса всей СХП с учётом запаса РТ, пускорегулирующей арматуры и элементов пневмоавтоматики составит

M _СХП = (1 + k _СХП ) n _БВД (1 + k _БВД ) M _{РТ 1} =

= (1 + k _СХП ) (1 + k _БВД ) M _РТ = μ _СХП M _РТ , (16) где k _СХП — коэффициент увеличения массы СХП за счёт пускорегулирующей арматуры и элементов пневмоавтоматики; k _БВД = M _БВД / M _{РТ 1} ≈ 0,138; μ _СХП = (1 + k _СХП ) (1 + k _БВД ).

Начальная масса МБ с учётом выражений (14), (16) и массы полезной нагрузки составит

М _КА0 =(1 + k _КА ) ( М _ПН + М _ЭДС + М _СХП ) =(1 + k _КА ) [ М _ПН + μ _ЭДС Р _ТС + ( μ _ЭДС Р _ЭРД + μ _ЭРД Р ^χ _ЭРД ) n _ЭРД + μ _СХП M _РТ ], (17)

где k _КА — коэффициент массы конструкционных элементов КА (корпуса, ферм крепления полезной нагрузки (ПН), бортового оборудования и т. п.),

М

КА0                                                 _χ

– М _ПН – µ _ЭДС Р _ТС = ( µ _ЭДС Р _ЭРД + µ _ЭРД Р _ЭРД )

1 + k _КА

определяющих массу конструкции МБ М _к , входящую в формулу (8).

Перепишем выражение (17) в следующем виде:

М РТ

.

^m ЭРД ДУ

^{+ µ} СХП ^М РТ

^{χ µ} ЭДС ЭРД   ^µ ЭРД ЭРД

.

^m ЭРД ДУ

Если пренебречь массой ЭРД, то это уравнение можно записать так:

М

КА0

ПН ^µ ЭДС ТС

1 + k _КА

^µ ЭДС    2

ЭРД ^µ СХП

^{2 η} ЭРД ^Т ДУ

^М РТ^.

^М РТ^.

С учётом массы ЭРД в общем виде имеем:

^М КА0

1 + k _КА

– М _ПН – µ _ЭДС Р _ТС

^µ ЭДС ^I ЭРД ^{2 η} ЭРД

₊ ^µ ЭРД ^.1– χ ^m ЭРД

ЭРД

^{2 η} ЭРД

М РТ

×

^{2 η} ЭРД ^Т ДУ

^µ ЭДС ^I ЭРД

^µ ЭДС ^I ЭРД ₊    ^µ ЭРД

.

^η ЭРД ДУ     ^m ЭРД ДУ

χ

+ µ

М РТ

СХП

^Т ДУ

I ²

^{= µ} ЭДС ^I ЭРД

+ ^{µ ЭРД (2 η ЭРД ) – χ}

1– χ ЭРД

.        2χ mЭРД ЭРД

^{2 η} ЭРД

^{+ µ} СХП

+ ^{µ ЭРД (2 η ЭРД ) 1– χ}

^.1– χ ^m ЭРД

2 χ 1– χ

ЭРД ЭРД     ^µ СХП ^η ЭРД ДУ

В основу расчёта запаса массы РТ на транспортную операцию МБ положено допущение о соответствии энергетического эквивалента перелёта, определяемого значением массы РТ, значению характеристической скорости операции V _х (формула Циолковского). Характеристическая скорость межорбитального перелёта V _х (без учёта энергозатрат на преодоление сопротивления атмосферы) определяется разностью орбитальных скоростей МБ на опорной V _о и на конечной (рабочей) V _р орбитах:

∆ V _х = | V _о – V _р |.

Следует отметить, что эта формула применима для круговых орбит. Вследствие влияния сопротивления атмосферы, несферичности Земли и возможного отключения электроракетной двигательной установки на теневых участках, форма спиральных витков траектории может значительно отклониться от круговой. Поэтому величина V _х применима только для оценки энергозатрат на перелёт.

На основе формулы Циолковского с использованием величин ∆ V _х и I _ЭРД

^М РТ

2 χ

ЭРД    ^µ СХП ^η ЭРД ДУ

М _РТ

^{2 η} ЭРД ^Т ДУ

.

×

можно оценить массу РТ на перелёт в направлении с ОО на РО:

M РТ = М КА0 [1–exp(– ∆ V х / I ЭРД )] ≈

≈ М КА0 ∆ V х / I ЭРД ,                         (20)

где учтены два первых слагаемых в разложении экспоненты, так как при полётах в ближнем космосе I _ЭРД >>  ∆ V _х .

Подставляя в выражение (18) значение М _РТ из формулы (20), получим

^М КА0 1 + k _КА

= ∆ V х

М ПН – µ ЭДС Р ТС

^µ ЭДС

^{2 η} ЭРД ^Т ДУ

^I ЭРД

₊ ^µ СХП ^I ЭРД

м

КА0.

Дифференцируя по I _ЭРД , получим следующее выражение для оптимального

удельного импульса:

опт

ЭРД

^µ СХП

ЭРД        ^T ДУ ^.

^µ ЭДС

Подставляя в уравнение (19) зна-

чение М _РТ из формулы (20), получим

М КА0		µ ЭДС Р ТС = ∆ V x	µ ЭРД(2 η ЭРД) – χ I Э χ РД µ ЭДС I ЭРД +             1 – χ F ЭРД	+ 2 µ СХП η ЭРД Т ДУ	КА0
1 + k КА	ПН			I ЭРД	2 η ЭРД Т ДУ

Дифференцируя по I _ЭРД , получим

^µ ЭРД^{(2 η} ЭРД^{) – χ I} Э ^χ Р ^– Д    ^{2 µ} СХП ^η ЭРД ^Т ДУ

^Ц ЭДС + ^Х------------------------

ЭРД                    ЭРД

= 0;

^µ ЭДС ⁺

^χµ ЭРД

^{2 η} ЭРД

1– χ

^F ЭРД ^I ЭРД

^I ЭРД ^{– 2 µ} СХП ^η ЭРД ^Т ДУ

= 0.

При χ = 1 формула для оптимального удельного импульса приобретает следующий вид:

_опт                 ^µ СХП

^I ЭРД    ^{2 η} ЭРД µ _ЭДС + µ _ЭРД ^T ДУ ^.

При χ ≠ 1 формулу для I _Э ^оп _Р ^т _Д можно записать в следующем виде:

опт ^I ЭРД

^µ СХП ^T ДУ

^{η ЭРД                  2 η} ЭРД     ^{1– χ}

^µ ЭДС   ^µ ЭРД ^χ

^F ЭРД ^I ЭРД

Выражение (23) не содержит характеристической скорости операции ∆ V _х вследствие принятого в уравнении (20) допущения. Кроме того, при условии пропорциональности массы ЭРД его мощности χ = 1, параметры, содержащие χ в показателях степени, становятся равными 1, и формула заметно упрощается. В тех случаях, когда χ ≠ 1 I _Э ^оп _Р ^т _Д можно рассчитать методом последовательных приближений, положив на первом шаге χ = 1.

В расчётах принимались значения параметров при перелёте с ОО высотой 300 км на РО высотой 20 000 км, изложенные в табл. 1.

Таблица 1

Параметры перелёта с опорной орбиты на рабочую

№ п.п.	Параметр		Значение
	Символ	Наименование, размерность
1	ТС	Мощность технических систем МБ, Вт	3 000
2	ЭРД	Сила тяги модуля ЭРД, Н	1
3	n ЭРД	Количество ЭРД в составе ЭРДУ, шт.	4
4	η ЭРД	КПД ЭРД	0,5
5	χ	Показатель степени в формуле (12)	0,75
6	μ ЭРД	Удельная масса ЭРД в формуле (12), кг/Вт	1,9·10–3 χ
7	ρСБ	Удельная масса СБ, кг/м2	1,6
8	ηСБ	КПД СБ	0,228
9	w АБ	Удельная энергоёмкость АБ, Дж/кг	5,544·105
10	БВД	Относительная масса баллонов высокого давления, кг БВД/кг РТ	0,138
11	СХП	Коэффициент массы СХП, кг СХП/кг РТ	0,2
12	μ СЭС	Коэффициент массы СЭС, кг/кВт	0,15
13	ъ k КА	Коэффициент массы конструкции МБ	0,125

При принятых исходных данных получим следующие значения основных проектных параметров:

I ^опт = 56 179 м/с; Р = 262,2 кВт;

ЭРД                   СБ

М CЭС = М СБ + М АБ = 2 693,7 кг;

М _РТ = 502,4 кг; n _БВД = 12; М _СЭС = 115 кг;

М _АБ = 1 371 кг; S _СБ = 826 м²;

М _СБ = 1 321 кг; М _КА0 = 7 100 кг.

При конструкционной проработке МБ с СЭРДУ следует более детально рассматривать компоненты конструкции, их энергопотребление и массу с целью уточнения энергомассовой модели буксира.

Тепловой режим работы солнечной батареи

Дифференциальное уравнение энергобаланса СБ, позволяющее рассчитать её температуру T _СБ , имеет следующий вид [19]:

dT _СБ

С ρ S = Q cos θ + Q + СБ СБ _dt        Sun          Phon

+ Q_RSun

Rad ^{– P} ЭРДУ ^{– K} АБ ^P АБ^,

где C — удельная теплоёмкость СБ; t — текущее время; Q_Sun — мощность теплового солнечного излучения; θ — угол между нормалью к СБ и направлением на Солнце в системе координат СБ; Q_Phon — мощность теплового излучения от подстилающей поверхности Земли; Q_RSun — мощность теплового cолнечного излучения, отражённого от подстилающей поверхности Земли; Q_Rad = ( ε _с + ε _об ) σ Т ⁴ _СБ S _СБ — мощность радиационного излучения СБ на обе стороны, здесь ε _с и ε _об — коэффициенты теплового излучения поверхности солнечной и обратной сторон СБ соответственно; σ — постоянная Стефана–Больцмана; P _ЭРДУ — мощность электропитания ЭРДУ; K _АБ = 1 — идёт зарядка АБ; K _АБ = 0 — АБ заряжена до энергии расчётной величины.

При нахождении КА в тени Земли уравнение энергобаланса СБ упрощается:

С ρ S ^{dT СБ} = Q – Q . (25) СБ СБ Phon Rad

В процессе решения задачи полёта МБ с СЭРДУ уравнения (24), (25) приводятся к конечно-разностной форме и решаются численно в итерационном процессе, позволяя определить температуру СБ.

На рисунке представлена модель МБ с СЭРДУ. При её разработке ставилась задача отображения специфических компонентов, присущих именно КА с СЭУ и нашедших отражение в расчётной модели [12, 20]. Масштабирование элементов конструкции в формате изображения не проводилось.

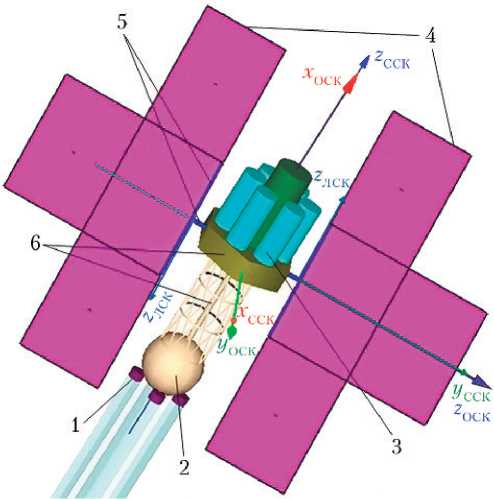
Расчётная модель межорбитального буксира (МБ) с солнечной электроракетной двигательной установкой: 1 — модуль электроракетного двигателя; 2 — система хранения и подачи рабочего тела; 3 — модуль полезной нагрузки; 4 — панели солнечных батарей (СБ); 5 — штанги поворота панелей СБ; 6 — элементы силовой конструкции МБ (ОСК — орбитальная система координат; ССК — строительная система координат МБ; ЛСК — локальная система координат СБ) (рисунок создан авторами)

Конструкция разработана в среде OpenGL и является элементом визуализации рабочей программы графического отображения полёта КА, входящего в состав программного комплекса моделирования межорбитальных перелётов КА с ЭРДУ.

уравнения движения МБ с малой тягой

Полёт МБ с ЭРДУ происходит в течение достаточно продолжительного времени и не сопровождается интенсивными манёврами вокруг центра масс (ЦМ) аппарата. Поэтому динамика полёта МБ может быть описана векторными дифференциальными уравнениями движения материальной точки в поле тяготения Земли, имеющими следующий вид в векторной форме:

→→ d\L

КА _ ЭРДУ ^   ^

dM^ A t) ^- а а ^- g З ;

dt    VКА где V→КА — вектор скорости МБ; R→ — радиус-вектор текущего положения МБ; F→ЭРДУ — вектор силы тяги ЭРДУ; →аа — вектор ускорения (точнее, замедления)

от силы аэродинамического сопротивления верхней атмосферы; М _КА ( t ) — текущая масса МБ; ^→ g _З — вектор ускорения МБ в поле тяготения Земли.

Полагается, что тяга маршевой ЭРДУ, работающей на изменение высоты полёта МБ, приложена по направлению его вектора скорости V ^→ _КА . Для увеличения высоты полёта вектор силы тяги должен быть приложен по вектору скорости, а для снижения КА — в противоположном направлении.

При полёте МБ его масса уменьшается вследствие расхода РТ на работу ЭРДУ в течение времени

M _КА ( t ) = M _КА (0) – m _ЭРДУ t ,            (27)

где m ^. _ЭРДУ — массовый расход РТ.

Гравитационное поле Земли рассчитывается по модели нормального поля тяготения, учитывающего вторую и четвёртую зональные гармоники [21] с потенциалом вида

^µ З ^µ 20                     ^µ 4 0

U _н = r + r ₃ P _{2 0} (sin ϕ ) + r ₅ P ₄₀ (sin ϕ ) ^,        (28)

где μ _З = 3,986·10¹⁴ м³/с²;

μ ₂₀ = –1,7555·10²⁵км⁵/с²;

μ ₄₀ = 1,563955·10³⁶ км⁷/с² — константы в разложении гравитационного поля Земли по полиномам Лежандра, определяющим широтную зависимость поля тяготения Земли; P ₂₀ (sin ϕ ) = 0,5(3sin² ϕ – 1); P ₄₀ (sin ϕ ) = 0,125(35sin⁴ ϕ – 30sin² ϕ + 3).

Вектор ^→ а _а в уравнениях (26) определяет ускорение от силы аэродинамического сопротивления атмосферы Земли:

^→ а _а = С _х ρ

V ^{→ 2} атм

2 M _КА ( t )

S , мид

где С _х — коэффициент аэродинамического сопротивления МБ; ρ — плотность атмосферы в месте нахождения МБ; S _мид — площадь миделевого сечения МБ в набегающем потоке; V ^→ _атм — скорость МБ с учётом вращения атмосферы вместе с Землей

→→   →

V _атм = V _АГСК + ^→Ω _З × R ,                   (30)

здесь V ^→ _АГСК — вектор скорости МБ в абсолютной геоцентрической системе координат (АГСК); ^→Ω _З — вектор угловой скорости вращения Земли; R ^→ — вектор текущего положения МБ.

В ГОСТ Р 25645.166–2004 [22] приведена методика расчёта коэффициента аэродинамического сопротивления КА С _х при полёте в верхней атмосфере в диапазоне 120…1 500 км. Соотношения модели позволяют вычислить нормальную и касательную компоненты силы аэродинамического сопротивления корпуса КА. При расчёте полёта МБ с СЭРДУ принята плоская панельная конструкция батарей. Поэтому площадь миделевого сечения СБ определена на основании следующего выражения:

S _{мид СБ} = cos ψ S _СБ , где ψ — угол между вектором скорости и нормалью к поверхности СБ.

Вклад в силу аэродинамического сопротивления корпуса МБ учитывается только для торцевой площади шестиугольной платформы (рис. 1), расположенной по нормали к вектору его скорости.

Здесь также следует иметь в виду, что для корректного расчёта сил аэродинамического сопротивления необходимо знание температуры поверхности наружных элементов конструкции МБ, главным образом, СБ Т _СБ [см. уравнения (24), (25)].

Несмотря на малое значение силы сопротивления верхней атмосферы, она может существенно повлиять на изменение параметров орбиты (высоты, эксцентриситета, аргумента перигея) за продолжительный интервал времени полёта, особенно на высотах ниже 800 км. Поэтому для модели КА с СБ эти факторы последовательно учитываются в баллистических расчётах.

Расчёт параметров верхней атмосферы в процессе полёта МБ с СЭРДУ выполнялся с использованием формул, приведённых в Модели стандартной атмосферы [23], применимых в диапазоне высот 120…1 200 км.

Для решения поставленной задачи межорбитального перелёта необходимо выбрать систему координат. Длительность перелётов МБ с СЭРДУ может составлять от нескольких суток до нескольких месяцев. За это время Земля не только совершит множество оборотов вокруг своей оси, но и существенно продвинется в своём движении вокруг Солнца. Поэтому представляется наиболее целесообразным использовать АГСК, в которой ось x _АГСК направлена из центра Земли в точку весеннего равноденствия ϒ , ось z _АГСК совпадает с осью вращения Земли, а ось y _АГСК дополняет систему координат до правой.

В пользу выбора АГСК говорит и то обстоятельство, что начальную и конечную орбиты МБ, как и систему координат АГСК, можно считать неподвижными относительно звёзд, что существенно упрощает расчётный алгоритм. Тем не менее, следует иметь в виду, что наблюдение за полётом МБ ведётся из наземного центра управления. Поэтому необходимо знать положение МБ и в относительной геоцентрической системе координат (ОГСК), связанной с вращающейся Землей, причём оси z обеих систем координат совпадают, а ось x _ОГСК направлена на Гринвичский меридиан.

Пересчёт компонент радиус-вектора положения МБ из АГСК в ОГСК выполняется по векторной формуле →→

R АГСК = Mtz ( γ ) R ОГСК ,                  (31)

где Mtz ( γ ) — матрица вращения вокруг оси z — имеет следующий вид:

cosγ – sinγ 0 MtZ( у) = sinγ cosγ 0 ,             (32) 0 V 0 1 здесь γ = ΩЗS; ΩЗ — угловая скорость вращения Земли вокруг своей оси; S — звёздное время на долготе полёта МБ.

Вычисление звёздного времени S выполняется по специальной математической процедуре, тесно связанной с расчётом эфемериды Солнца и текущего положения радиус-вектора Земля – Солнце относительно направления в точке весеннего равноденствия [24]. Знание положения Солнца особенно необходимо при расчёте полёта МБ с СЭРДУ.

Система уравнений (24)–(32) должна быть дополнена граничными условиями (параметрами начальной и конечной орбит) и начальными условиями (координатами точки старта КА на начальной орбите R ^→ _КА0 и компонентами скорости в этой точке V ^→ _КА0 в момент времени старта t = 0).

основные соотношения процессов управления ориентацией СБ

При выполнении целевой программы полёта МБ, оснащённого СБ, актуальной становится задача определения оптимальной ориентации СБ, обеспечивающей максимальную плотность потока излучения Солнца на её поверхность.

Решение задачи управления ориентацией СБ предполагает известными в расчётный момент времени:

• •    положение центра масс (ЦМ) МБ на орбите и, соответственно, его текущей орбитальной системы координат (ОСК);

• •    ориентацию МБ в ОСК, т. е. положение его строительной системы координат (ССК) в ОСК;

• •    направление на Солнце из ЦМ МБ в абсолютной или относительной геоцентрической системе координат, определённое единичным вектором S ^→ _АГСК или S _ОГСК ;

• •    ориентацию СБ в ССК МБ, характеризуемую положением ССК СБ в ССК МБ.

Вариант оптимальной ориентации СБ на Солнце, имеющей две управляемых степени свободы [первую — относительно оси у ССК (поворот всей СБ на 360 ° ), а вторую — вокруг оси локальной строительной системы координат (ЛСК) z _ЛСК (синхронные повороты правой и левой панелей СБ в диапазоне ±90 ° )], рассмотрим на конкретном примере МБ, образ которого показан на рис. 1.

Считаются известными: положение ССК МБ, определённой в его ОСК единичным в _→ ектором (1-вектор) с компонентами A = ( А , А , А );

ССК xССК, yССК, zССК направление 1-вектора ориентации СБ в ССК МБ B→  = (B   , B , B );

ССК      xССК,    yССК,    zССК направление 1-вектора ориентации Солн-→ ца в ССК МБ SССК = (SxССК, SyССК, SzССК). Здесь полагаем, что узел крепления СБ совпадает с ЦМ МБ.

Поскольку ось поворота СБ жёстко связана с корпусом МБ через подшипниковые узлы, то поворот возможен только вокруг оси у _сск на угол ± Р к оси x _CСК . После поворота батареи формула ориентации 1-вектора СБ может быть конкретизирована в виде

В ССК = (cos p , 0, sin p ).                   (33)

Угол а между 1-вектором направления на Солнце и 1-вектором ориентации СБ можно определить через скалярное произведение этих векторов:

cos a = S x _ССК cos p + S z _ССК sin p .         (34)

Очевидно, что максимальная освещённость СБ Солнцем будет достигнута при минимальном ^ значении угла а между 1-вектором S _ССК и осью x _ССК , соответствующем максимальному значению cos a . Для нахождения угла Р *, определяющего конечное положение панелей СБ и, соответственно, экстремальную освещённость её поверхности, следует продифференцировать эту формулу по Р и приравнять результат нулю. Выполнив эту процедуру, найдём

• -    S x _ССК sin p * + S z _ССК cos P * = 0;

S

• р * = arctg . S x ССК

Таким образом, угол Р * определяет проекцию направления Солнца на плоскость ( xz ) _ССК МБ. Подставляя значение угла Р * в уравнение (34), найдем угол а *, на который следует довернуть СБ вокруг оси y _ССК МБ. Здесь, однако, возникает определённая сложность, связанная с тем, что формула (35) определяет величину угла Р * в диапазоне ±90 ° с точностью до 180 ° . То есть этому значению может отвечать как максимальная, так и минимальная освещённость панелей. Для получения максимального результата следует обратиться к анализу второй производной от выражения (34).

Как известно, максимуму функции соответствует отрицательное значение её второй производной. Поэтому условие максимума имеет вид

D (   a)

d \V

= — S x сск cos P * —

— S z ССК sin e * < 0.

Если ^ угол в * и оба компонента вектора S _ССК положительны, то условие максимума (36) выполняется автоматически. При отрицательных значениях следует выполнить дополнительное исследование выражения (35) с анализом знаков и значений компонент вектора направления на Солнце. Так, если угол в * отрицательный, то его следует переопределить по формуле в * ' = 180 ° + в *-

Если панели СБ обладают второй степенью свободы, т. е. могут вращаться вокруг штанг крепления, ориентированных вдоль осей z _ЛСК , то панели можно довернуть на угол у для улучшения энергетических показателей СБ. Принцип расчёта в этом случае аналогичен рассмотренному выше, однако следует перейти в ЛСК СБ, повёрнутой вокруг оси y _ССК , и учесть ограничение на углы поворота панелей батарей вокруг штанг крепления.

Из приведённых выражений видно, что направление и величина угла поворота СБ зависят от текущих значений компонент 1-вектора ориентации Солнца в ССК МБ. Таким образом, отслеживая положение Солнца в процессе полёта МБ по орбите и поворачивая СБ на углы а * и у , получим наилучшую реализацию подсветки СБ излучением Солнца.

Межорбитальный перелёт МБ с СЭрду

В качестве примера практического применения описанных выше моделей рассмотрим межорбитальный перелёт МБ с СЭРДУ, выполняющего задачу доставки полезного груза массой 2 000 кг с ОО высотой 300 км на орбиту высотой ≈20 000 км. Полагалось, что ЭРДУ включает четыре модуля с ЭРД с удельным импульсом 40 000 м/с, тягой модуля по 1 Н и КПД = 0,5; рабочее тело ЭРД — ксенон.

Расчётная мощность электропитания ЭРДУ Р _ЭРДУ = 160,0 кВт.

Были приняты следующие характеристики элементов конструкции МБ: удельная мощность СЭУ 315 Вт/м2, что соответствует КПД СБ 23%; удельная масса СЭУ 1,6 кг/м2; удельная масса аккумуляторной литий-ионной батареи 5,544·105 Дж/кг [15]; теплоёмкость СБ 600 Дж/(кг·К). В результате расчёта получены следующие энергомассовые параметры СЭУ: мощность 185 кВт (с учётом 15% на электропитание бортовых потребителей и резерв); площадь 587 м2; масса 940 кг.

Траектория полёта МБ с ЭРДУ имеет вид раскручивающейся спирали, содержащей сотни витков. Поэтому при решении задач предполагалось сохранение результатов с заданным шагом по высоте (~500 км), соотнесённых с моментами времени пересечения плоскости экватора и перехода траектории из Южной полусферы мира в Северную. Расчёты выполнялись в специализированном программном комплексе, позволяющем варьировать в широком диапазоне как траекторные параметры полёта МБ, так и их конструктивные характеристики.

Рассматривались четыре варианта решения задачи перелёта:

Вариант 1. В составе бортового оборудования МБ имеется АБ ёмкостью, достаточной для обеспечения непрерывной работы ЭРДУ в течение всей продолжительности начального витка траектории. В этом варианте ЭРДУ работает на всей траектории перелёта.

Вариант 2. В составе бортового оборудования МБ имеется АБ ёмкостью, достаточной для обеспечения непрерывной работы ЭРДУ в течение всей продолжительности конечного витка траектории. ЭРДУ отключается на теневых участках при израсходовании энергетического запаса в АБ.

Вариант 3. В составе бортового оборудования МБ отсутствует АБ для энергообеспечения ЭРДУ.

Вариант 4. В составе бортового оборудования МБ отсутствует АБ для энергообеспечения ЭРДУ. Время старта выбирается с учётом минимальной продолжительности полёта в тени Земли.

В вариантах 1–3 КА стартует из точки перигея ОО 20.04.2020 г. в 15:00:00.

В варианте 4 КА стартует из точки перигея ОО 20.04.2020 г. в 7:00:00. После достижения заданной высоты на РО от МБ отделяется полезная нагрузка, он разворачивается на 180 ° и возвращается на исходную высоту ОО.

Расчётные баллистические характеристики вариантов перелёта показаны в табл. 1. Здесь следует отметить, что сразу рассчитать массу РТ на всю операцию для любого варианта не представляется возможным. Поэтому была реализована итерационная процедура последовательного уменьшения начальной массы РТ и, соответственно, массы системы его хранения и подачи в ЭРД. Именно эти данные и представлены в табл. 2.

Анализ траектории полёта МБ с СЭРДУ показывает существенное влияние АБ на результаты операции. Её масса и соответствующее утяжеление конструкции приводит к увеличению длительности перелёта на 20 сут и более, значительному увеличению массы СБ и РТ и в целом стартовой массы КА ( варианты 1 , 2 ).

Другим специфическим фактором является увеличение эксцентриситета витков траектории, особенно проявляющееся на траектории, содержащей длительные участки полёта на теневой стороне с неработающими ЭРД ( варианты 2 , 3 ). В этих вариантах реализуется наибольший эксцентриситет. В свою очередь, в варианте 1 ЭРДУ работает непрерывно на всей траектории, включая теневые участки, а в варианте 4 выбрано время запуска, обеспечивающее лишь кратковременные теневые участки, а более 90% времени полёт выполняется на освещённой Солнцем траектории, т. е. при непрерывной работе ЭРДУ. Именно непрерывный или близкий к нему режим работы ЭРДУ обеспечивает наименьший эксцентриситет витков траектории полёта МБ. Тем не менее, как показывает детальный анализ результатов расчёта, наличие СБ большой площади оказывает существенное влияние на формирование траектории полёта КА на высотах до 400 км при его движении в зонах выхода из тени и захода в тень, где влияние парусности батарей наиболее заметно.

Таблица 2

расчёт вариантов транспортной операции для МБ с СЭрду

Параметры	Варианты
	1	2	3	4
Время полёта на теневом участке первого витка, с	2 192	3 312	2 192	2 505
Энергозатраты ЭРДУ на работу на теневом участке, запасаемые в АБ, МДж	403, 3	609,4	0	0
Масса АБ, кг	727,4	1 099	0	0
Мощность СБ, отводимая на зарядку АБ, кВт	125	15,5	0	0
Расчётная мощность СБ, кВт	309	200	184	184
Площадь СБ, м2	981	633,4	585	585
Масса СБ, кг	1 569	1 013	935	935
Начальная масса рабочего тела при старте с ОО, кг	873	756	463	504
Продолжительность прямого перелёта, сут	65,1	66,8	47,9	44,9
Апогей РО, км	20 149	20 159	20 322	20 279
Перигей РО, км	19 328	14 813	12 560	18 340
Количество витков при прямом перелёте	493	551	401	368
Продолжительность обратного перелёта, сут	37,2	34,8	19,125	17,9
Апогей ОО при возвращении, км	421,8	968	863	1 241
Перигей ОО при возвращении, км	293	296	300	287
Количество витков при возвращении на ОО	272	265	152	134
Масса рабочего тела при возвращении на ОО, кг	3,5	0,2	1,2	1,34
Начальная масса МБ, кг	6 061	5 690	3 952	4 010

Очевидно, что вариант 4 является наиболее приемлемым по энергомассовым показателям и продолжительности перелёта. Результаты расчёта перелёта МБ с ОО на РО по варианту 4 показаны в табл. 3. Строки № 1–7 показывают динамику формирования витков с возрастанием эллиптической составляющей. Баллистические характеристики межорбитального пе в направлении опорная орбита ^ рабочая орбита (ва]						Этот процесс продолжается до 195-го витка, где эксцентриситет достигает значения ~0,0702. На этом участке траектории ещё есть теневые участки, где ЭРДУ не работает, но их длительность уменьшается, а начиная с 220-го витка полёт межорбитального буксира происходит по траектории, полностью освещённой Солнцем. Таблица 3 релёта МБ с СЭрду иант 4)
№ п/п	Дата и время	№ витка	М РТ , кг	H КА , км	V КА ,км/с	H а , км	H п , км	Ш „ , °	П °	э , °	Т орб , мин	Р з . °
1	20.04.2020 07:00:15	1	503,3	299,3	7,730	299,9	299,1	–44	59,9	45	90,36	0
2	20.04.2020 08:30:30	2	502,9	303	7,729	307,7	302,3	–138,6	–142,1	317,8	90,48	0
3	20.04.2020 10:00:45	3	502,6	306,8	7,728	315,8	305,1	–133,9	–165,6	313,6	90,59	0,1
4	20.04.2020 13:02:00	5	501,9	314,6	7,726	332,5	310,8	–131,6	148,9	310,9	90,82	0,2
5	20.04.2020 16:03:30	7	501,2	322,7	7,723	349,3	316,9	–129,9	102,4	309,6	91,05	0,4
6	20.04.2020 19:05:30	9	500,5	331,2	7,720	366,4	323,1	–128,6	50, 6	308,6	91,29	0,5
7	21.04.2020 16:34:00	23	495,5	395,8	7,695	491,6	371,0	–126,2	89,9	305,6	93,6	1,4
8	23.04.2020 00:00:15	43	488,0	505,5	7,648	684,6	451,8	–122,7	–27,7	301,8	95,88	2,7
9	26.04.2020 23:34:00	100	462,8	954,8	7,427	1 334,0	781,6	–109,9	–39,1	289,9	106,2	6,6
10	02.05.2020 09:46:15	168	423,9	1 838,2	7,007	2 383,4	1 479	–99,3	149,6	278,9	125,4	11,9
11	10.05.2020 16:53:45	250	355,0	3 875,1	6,253	4 497,1	3 359	–92,2	22,3	272,2	173,3	20,1
12	15.05.2020 08:44:30	285	314,7	5 422,8	5,825	6 075,2	4 861	–91,4	136,6	271,4	213,6	24,7
13	20.05.2020 08:54:45	315	271,4	7 526,9	5,363	8 221,7	6 914	–91,1	127,0	270,9	272,9	29,6
14	25.05.2020 13:49:15	339	226,5	10 407	4,879	11 151	9 734	–90,6	46,9	270,5	361,6	34,8
15	30.05.2020 03:50:00	357	181,0	14 379	4,386	15 178	13 644	–90,3	–52,2	270,3	496,9	40,0
16	01.06.2020 06:44:30	361	168,5	15 729	4,250	16 544	14 979	–90,4	145,7	270,3	546,1	41,4
17	02.06.2020 21:08:30	365	154,7	17 389	4,099	18 220	16 622	–90,4	71,9	270,3	608,6	43,0
18	03.06.2020 18:03:00	367	147,2	18 376	4,016	19 214	17 600	–90,3	–26,5	270,3	646,9	43,8
19	04.06.2020 12:01:45	368	140,7	20 001	3,835	20 279	18 340	–85,7	–53,0	317,0	682,6	44,6

Примечание. М _РТ — масса топлива; H _КА, V _КА — контрольная высота и скорость полёта МБ; H _а, H _п — высота апогея и перигея витка соответственно; ю _п — аргумент перигея; П — долгота восходящего узла; Э — истинная аномалия; Т о _рб — период орбиты; Р З — угол поворота Земли вокруг Солнца.

Здесь ЭРДУ работает непрерывно, эксцентриситет витков уменьшается и на последнем витке равен 0,0377.

Аналогичные тенденции проявляются и в вариантах 1–3 . В варианте 1 результирующий эксцентриситет РО наименьший, так как ЭРДУ работает непрерывно на всей траектории. Однако высокая стоимость этого варианта исключает его реализацию. Также следует отметить, что во всех вариантах перигейные участки витков смещаются к освещённой части траектории, а апогейные — к теневой. Причиной такой ситуации является значительная площадь СБ, приводящая к торможению МБ на низких участках траектории и частичной работе ЭРДУ на её теневых участках.

В процессе расчётов также вычислялись участки приложения силы тяги ЭРДУ на освещённой и теневой сторонах траектории, значения температуры СБ на различных этапах полёта и силы аэродинамического сопротивления КА вследствие влияния верхней атмосферы Земли. Фрагменты соответствующих расчётных данных показаны в табл 4.

Таблица состоит из двух частей: левая часть — результаты расчёта полёта МБ на первых двух витках; правая часть — на последнем витке. В расчётах использовалась простая модель радиационного нагрева/охлаждения плоской тонкой панели, имеющей рассчитанную массу и заданную теплоёмкость. Учитывались энергетические потоки от Солнца на освещённой стороне и тепловой поток от Земли на всей траектории. Согласно расчётным данным, температура СБ вполне коррелирует с положением МБ на освещённой и теневой сторонах траектории полёта, колеблясь от 350 до 180 К. Анализ результатов расчётов подтверждает, что наибольшее аэродинамическое торможение МБ испытывает, когда СБ перпендикулярны вектору скорости в областях выхода из тени Земли или входа в неё.

Учёт сопротивления атмосферы выполнялся до высоты 1 200 км, хотя реально её влияние можно было ограничить высотой ~900 км. Как следует из результатов расчёта, сила аэродинамического сопротивления МБ, обусловленная в общем случае переменной ориентацией СБ относительно направления полёта, может заметно меняться в течение полёта на каждом витке. Анализ зависимости этой силы от параметров перелёта представляет отдельный интерес, например, в упрощённых оценках времени перелёта МБ.

Таблица 4

результаты расчёта параметров Ка на начальном (слева) и конечном участках траектории, вариант 4

№ витка	t , с	H KA , км	у , °	F атм , Н	T СБ , K	№ витка	t , с	H KA , км	т . к СБ,
1С	15	299,3	125,1	0,2017	304,7	368 С	3 894 000	18 376	310,1
1С	1 005	295,1	63,7	0,1543	337,1	368 С	3 895 005	18 477	310,3
1С	2 010	292,6	20,2	0,1908	322,7	368 С	3 896 010	18 596	310,3
1Т	3 000	295,1	71,8	0,0857	208,7	368 С	3 897 000	18 726	310,2
1Т	4 005	298,2	133,8	0,2402	197,7	368 С	3 898 005	18 869	310,0
1С	5 010	302,9	149,4	0,2035	320,6	368 С	3 899 010	19 019	309,8
2С	6 000	300,4	90,2	0,0008	336,1	368 С	3 900 000	19 171	309,6
2С	7 005	296,5	30,3	0,2326	329,8	368 С	3 901 005	19 325	309,3
2Т	8 010	300,9	46,6	0,2270	255,2	368 С	3 902 010	19 477	309,1
2Т	9 000	304,7	107,8	0,0664	197,4	368 С	3 903 000	19 620	308,8
2С	10 005	307,5	160,0	0,1342	259,8	368 С	3 904 005	19 756	308,6
2С	11 010	305,9	116,1	0,1208	330,2	368 С	3 905 010	19 881	308,4

Примечание. С и Т — солнечная и теневая части траектории соответственно; t — текущее время полёта; H KA — высота КА; у — угол между вектором скорости и нормалью к СБ; F _ат м — сила аэродинамического сопротивления; T _СБ — температура СБ.

обратный перелёт МБ с СЭрду с рабочей орбиты на опорную

В табл. 5 представлены результаты баллистического расчёта обратного перелёта КА с РО на ОО по варианту 4 . Предполагается, что на РО была отделена полезная нагрузка и выполнен разворот МБ на 180 ° так, что ЭРДУ будет тормозить движение.

Как видно из табл. 5, продолжительность обратного перелёта оказывается в два раза короче прямого, а количество витков снижения почти в три раза меньше прямого перелёта, главным образом за счёт отсоединения полезной нагрузки и израсходования значительной массы РТ. При этом наибольшая скорость снижения реализуется на высотах ниже 900 км.

Данные табл. 5 также свидетельствуют о значительном эксцентриситете (~0,067) конечной орбиты МБ. Эксцентриситет спиральных витков начинает увеличиваться при появлении участков тени Земли на траектории полёта снижающегося МБ. Причины этого явления подобны рассмотренным — отключение ЭРДУ в тени и неравномерное аэродинамическое сопротивление верхней атмосферы.

Конечно, эксцентриситеты рабочей и конечной орбит при возвращении могут быть скорректированы организацией работы ЭРДУ по специальной программе. Но на эту работу потребуется дополнительное время и запас РТ.

заключение

Рассмотрены модели МБ с СЭРДУ, учитывающие только наиболее значимые конструкционные факторы при наличии и отсутствии бортовой аккумуляторной батареи для питания ЭРДУ на теневых участках, и модель компланарного полёта на рабочую орбиту с возвращением к Земле. Анализ результатов моделирования позволяет сделать следующие выводы:

• 1.    При конструировании космических аппаратов с ЭРДУ и СЭУ необходимо подбирать траекторию полёта, содержащую теневые участки минимальной длительности, выбором времени начала операции.

• 2.    Большая площадь поверхности солнечных батарей и наличие теневых участков с неработающей ЭРДУ приводят к заметному эксцентриситету конечных орбит при полётах в обоих направлениях.

  Таблица 5

  Баллистические характеристики межорбитального перелёта МБ с СЭрду в направлении рабочая орбита ^ опорная орбита (вариант 4)

  № п/п	Дата и время	№ витка	М РТ , кг	H КА , км	V КА ,км/с	H а , км	H п , км	Ш п , °	О °	9 , °	Т орб, мин	Р з - °
  1	04.06.2020 16:19:15	1	139,2	19 013	3,950	20 156	17 534	–100,3	118	280,3	664	44,7
  2	08.06.2020 04:25:15	11	108,9	11 672	4,682	12 545	10 521	–101,1	–66	281,1	397	48,2
  3	12.06.2020 00:28:15	29	75,8	6 695	5,499	7 412	5 756	–101,7	–12	281,3	244	52,0
  4	16.06.2020 01:55:45	59	43,6	3 437	6,379	3 948	3 953	–91,6	–40	271,3	161	56,0
  5	20.06.2020 01:25:00	101	16,8	1 335	7,311	1 887	1 316	–158,1	–43	338,1	118	59,9
  6	21.06.2020 00:13:00	113	10,8	926	7,553	1 604	625	–176,3	–29	356,0	110	60,8
  7	22.06.2020 01:07:30	127	4,6	510	7,827	1 359	506	–7,7	133	8,6	103	61,9
  8	22.06.2020 14:33:00	134	1,3	299	7,978	1 240	286	–140,1	109	346,2	99	62,4

  Примечание. М _РТ — масса топлива; H _КА, V _КА — контрольная высота и скорость полёта МБ соответственно; H _а, H _п — высота апогея и перигея витка соответственно; го п — аргумент перигея; О — долгота восходящего узла; 9 — истинная аномалия; Т о _рб — период орбиты; Р З — угол поворота Земли вокруг Солнца.

  
  

• 3.    В ряде случаев целесообразно отказаться от применения АБ для энергообеспечения ЭРДУ на теневых участках траектории полёта.

• 4.    Окончательное решение по составу бортового оборудования может быть принято на основе комплексного подхода к оценке результатов функционирования вариантов реализации состава оборудования МБ с учётом безотказности работы системы электроснабжения МБ и ЭРДУ в течение всего срока активного существования.