Моделирование периодических колебаний миграционной динамики: агент-ориентированный подход

Миграция является составной частью демографических процессов, определяющих не только количество, но и качество населения территории [6]. Даже в случае, когда миграционное сальдо региона или страны близко к нулю, происходит частичное замещение местного населения на мигрантов, зачастую являющихся носителями иной культуры, имеющих другой уровень образования и квалификацию. Миграционные процессы неизбежно приводят к сложной социокультурной и экономической трансформации территорий, поэтому анализ и прогнозирование механического движения населения не теряет актуальности в аспекте фундаментальных и прикладных научных исследований [2].

Традиционные подходы в изучении миграции базируются на выявлении качественных и количественных оценок связи миграции и социально-экономических процессов. В таких подходах предполагается, что макроэкономические тенденции формируют миграционные потоки, и в ряде случаев (особенно связанных с трудовой миграцией) это подтверждается эмпирически [1, 10, 15]. Несмотря на это, не выявлено строгой универсальной зависимости между динамикой социально-экономических показателей и миграцией населения [12].

Задача повышения эффективности аналитико-прогнозного инструментария миграции может быть решена с учетом анализа миграционного поведения. Релевантным методом для решения этой задачи является агент-ориентированное моделирование, на основе которого в социальных науках удалось объяснить феномен расовой сегрегации [16], распространение мнений и идеологий [14], поведение потребителей [7] и т.д. Ключевой идеей агент-ориентированного подхода является формирование социально-экономических тенденций макроуровня из совокупного поведения множества различных агентов [3, 9].

Изучение миграции методом агент-ориен-тированного моделирования начато сравнительно недавно. Одним из представителей отечественных научных школ этого направления является коллектив Центрального экономико-математического института РАН под руководством В.Л. Макарова и А.Р. Бахтизина [4]. Коллективом разработана демографическая модель, в которой миграция моделируется путем сочетания общих алгоритмов выбора агентами регионов с наилучшим уровнем экономического развития, низким уровнем безработицы и вероятностных характеристик (например, наличие семьи). Другим представителем направления исследования миграции методом агент-ориен-тированного моделирования является коллектив

Дальневосточного федерального университета под руководством Ю.Д. Шмидта [13]. В работе этого коллектива используется сочетание клеточного автомата и вероятностных процессов. В зарубежных исследованиях агент-ориентированные модели миграции также содержат различные критерии выбора территории мигрантами [4, 8].

Общими характеристиками современных агент-ориентированных моделей миграции является их прикладная направленность и учет многих экзогенных и эндогенных факторов движения населения. С одной стороны, такие подробные модели позволяют решать конкретные прикладные задачи, но, с другой стороны, сложность моделей не всегда позволяет выявить общие фундаментальные закономерности. В этом аспекте представляет отдельный интерес то, могут ли агенты с определенными стратегиями поведения формировать сложную (и при этом прогнозируемую) демографическую динамику. В частности, возможно ли с помощью агент-ориентированного моделирования качественно описать наблюдаемые на практике циклические колебания миграции [12] без введения в модель экзогенного циклического фактора.

Описание агент-ориентированной модели

Для исследования динамических режимов численности населения, формируемых только стратегиями миграционного поведения и неизменяемыми внешними условиями, рассмотрим гипотетическую систему трех регионов с агентами, мигрирующими между этими регионами. В данной модели выделены шесть возрастных групп агентов: 16–23 года, 24–31 год, 32–39 лет, 40–47 лет, 48–55 лет, 56–63 года. На каждый возраст с шагом 1 год приходится по три агента, что составляет 144 агента. В результате численных экспериментов нами определено, что такая численность агентов достаточна для описания различных режимов динамики. У представителей каждой возрастной группы есть стратегия миграционного движения по регионам с целью максимизации одного из трех индексов привлекательности региона: экономического, социального или экологического. Выделение именно таких индексов соответствует общей практике моделирования миграции [1, 13]. Каждый регион оценен по трехбалльной шкале (А – наивысший класс, В – средний класс, С – низкий класс) для каждого индекса привлекательности. Оценки выбраны таким образом, чтобы каждый регион лидировал только по одному индексу (табл. 1). Представляет интерес, как будут распределяться агенты по регионам в результате реализации групповых стратегий и линейного

Таблица 1

Оценки каждого региона по трехбалльной шкале исходя из индексов экономической, социальной и экологической привлекательности

Table 1

Assessment of each region on a three-point scale, based on the indices of economic, social and environmental attractiveness

Индекс привлекательности 1 регион 2 регион 3 регион Экономической A B C Социальной B C A Экологической C A B изменения численности различных возрастных групп.

Рассмотрены шесть стратегий выбора региона, которые подразделяются на чистые и смешанные (табл. 2). Чистые стратегии (1-3) заключаются в стремлении мигранта выбрать регион только с одним наивысшим индексом привлекательности. Смешанные стратегии (4-6) заключаются в желании агента выбрать регион, максимально удовлетворяющий двум индексам привлекательности: экономическому и социальному, экономическому и экологическому, экологическому и социальному. Также полагается, что для каждой возрастной группы агентов характерна одна стратегия поведения. Перемещение мигрантов между регионами осуществляется через определенный промежуток времени исходя из выбора и реализации конкретной стратегии. Например, агенты 32–39 лет стремятся выбрать регион с наивысшим индексом экономической привлекательности (стратегия 1). Для этого они последовательно перемещаются в первый регион, который имеет наибольшее значение данного индекса по сравнению с остальными.

Таким образом, алгоритм агент-ориентиро-ванной модели можно записать в следующем виде:

• 1.    Заполняем массив с агентами для каждого региона (табл. 3).

• 2.    Задаем значение T – прогнозный период моделирования, c шагом один год.

• 3.    Рассматриваем первого агента.

• 4.    Если возраст агента больше A_max (в данном случае A_max =63), то замещаем его на A_min – летнего агента ( A_min не обязательно должен быть минимальный возраст, это может быть любое значение, меньшее A_max ).

• 5.    Если агент перешел в следующую возрастную группу, то меняем его стратегию (см.

• 6.    Если агент определенное количество времени N (лет) находится в одном регионе, то осуществляем переход в следующий регион согласно текущей стратегии агента (см. табл. 2), где N – шаг перехода.

• 7.    Увеличиваем возраст агента на один год.

• 8.    Переходим к следующему агенту, если рассмотрели не всех агентов, то возвращаемся к пункту 4.

• 9.    Записываем данные о каждом агенте в отдельный массив.

• 10.    На этом заканчивается один шаг моделирования, переходим к следующему шагу и, если не достигли значения T, то возвращаемся к пункту 3.

• 11.    Вывод статистических данных.

Таблица 2

Стратегии агентов по выбору региона

Table 2

Strategies of agents for choosing the region

Стратегии миграции по регионам Возрастная группа Первый шаг (регион) Второй шаг (регион) Третий шаг (регион) 1 – наивысший индекс экономической привлекательности 32–39 3 2 1 2 – наивысший индекс социальной привлекательности 24–31 2 1 3 3 – наивысший индекс экологической привлекательности 16–23 1 3 2 4 – наивысший индекс экономической и социальной привлекательности 48–55 2 или 3 1 - 5 – наивысший индекс экономической и экологической привлекательности 40–47 3 или 1 2 - 6 – наивысший индекс социальной и экологической привлекательности 56–63 1 или 2 3 - табл. 2).

Для реализации этого алгоритма на ЭВМ написана соответствующая программа на языке Delphi 7.0. Она позволяет строить прогнозные сценарии динамики численности агентов и выводить статистические данные по всем регионам для каждой возрастной группы. Отметим, что данная модель полностью детерминирована и результат каждого вычислительного эксперимента однозначен.

Результаты вычислительных экспериментов

Рассмотрим результаты вычислительных экспериментов, полученных на основе предложенной модели. Для того чтобы исключить влияние на динамику численности начального распределения агентов, в качестве исходных данных рассмотрено равномерное распределение разновозрастных агентов каждого региона (табл. 3). В модели использовался равномерный шаг перехода в другой регион, равный N=2 года. В модели принято, что каждые два года агенты переходят в другой регион согласно текущей стратегии поведения. Вычислительные эксперименты показали качественную идентичность результатов при разной длине шагов перехода.

В модели принято, что агенты старше 63 лет выводятся из системы и замещаются на агентов

Таблица 3

Table 3

Массив с агентами для каждого региона

Array with agents for each region

№ агента	1	2		48	46	47		96	91	92		144
Возраст	16	17		63	16	17		63	16	17		63
Регион	1	1	1	1	2	2	2	2	3	3	3	3

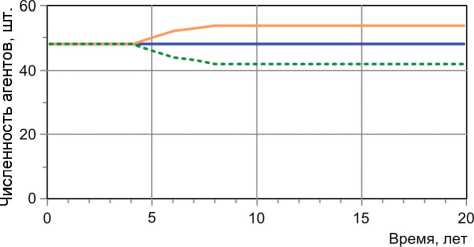
других возрастных групп. При замещении агентов старше 63 лет на 16-летних через некоторый временной интервал получаем стационарные значения численности рассматриваемых групп населения трех регионов (рис. 1). При этом регионы 2 и 3 оказываются конкурирующими, и регион 2 «перетягивает» на себя часть населения региона 3. Это объясняется тем, что согласно соответствующей стратегии поведения агенты 63 лет концентрируются в 3 регионе и замещаются на 16-летних, которые все перемещаются на место выбывших в 3-й регион (в начальном распределении их численность одинакова во всех трех регионах). Затем все 18-летние согласно их стратегии поведения сразу оказываются в регионе 2, не задерживаясь в регионе 3 (см. табл. 2).

Далее проведена серия численных экспериментов, направленная на изучение динамики численности рассматриваемых групп населения в трех модельных регионах при условии замещения 63-летних агентов на агентов различных возрастных групп. Такая ситуация может сложиться, например, вследствие соответствующей миграционной политики. В итоге получено, что при замещении 63-летних агентов 24-летними из рассматриваемой системы постепенно «выводится» когорта 16–23 лет и в численности населения трех модельных регионов наблюдаются периодические колебания (рис. 2а). Похожие колебания наблюдаются при замещении агентов 63 лет агентами различных возрастных групп (рис. 2б, в). При этом замещение 40-летними агентами приводит к возникновению в системе неожиданного эффекта,

Регион 1 Регион 2 -- Регион 3

Рис. 1. Динамика численности населения в трех модельных регионах при замещении 63-летних агентов на 16-летних

• Fig. 1.    Population dynamics in three model regions when replacing 63-year-old agents with 16-year-olds

когда численность населения трех модельных регионов достигает одинаковых стационарных значений. Замещение агентами старше 40 лет также приводит к периодическим колебаниям. В процессе замещения 63-летних на 52-летних и старше также наблюдается достижение стационарного значения, но с обнулением численности одного или двух модельных регионов (рис. 2д, е).

Таким образом, при равномерном распределении численности населения численность агентов в модельных регионах достигает стационарных значений. При замещении 63-летних на агентов старше 16 лет наблюдаются как периодические, так и стационарные режимы динамики с возможным обнулением численности населения одного или двух модельных регионов. Такие режимы динамики численности населения связаны с нарушением баланса стратегий в системе. Выведение отдельных возрастных групп из системы производит «провалы» численности населения. Если это выведение групп из системы носит долгосрочный характер, то «провалы» приобретают характер периодических колебаний, в том числе и в возрастной структуре (рис. 3).

Следует еще раз подчеркнуть, что в описанной модели число агентов неизменно, т.е. не учитываются особенности естественного движения населения. В реальной системе могут происходить колебания рождаемости и смертности, моделирование которых является отдельной нетривиальной задачей. При этом, как показано в работе [11], период колебаний, связанных с естественным движением населения, может быть значительно больше периода колебаний в миграционных процессах. Это означает, что в данной модели для конкретного региона или страны могут наблюдаться колебания численности населения с разным периодом, образуемые в результате суперпозиции демографических волн разной длины. Кроме того, в проведенных численных экспериментах был обнаружен интересный эффект: при вытеснении агентов одной возрастной группы во всех модельных регионах динамика численности агентов описывается ломаной линией (рис. 2а), при этом вытеснение агентов разных возрастных групп в каждом модельном регионе соответственно приводит к сглаживанию данной модельной кривой (рис. 2б, в). Этот эффект дает основание полагать, что более детальный учет демографических и социально-экономических процессов в модели для конкретного региона даст возможность описать широкий спектр динамических режимов.

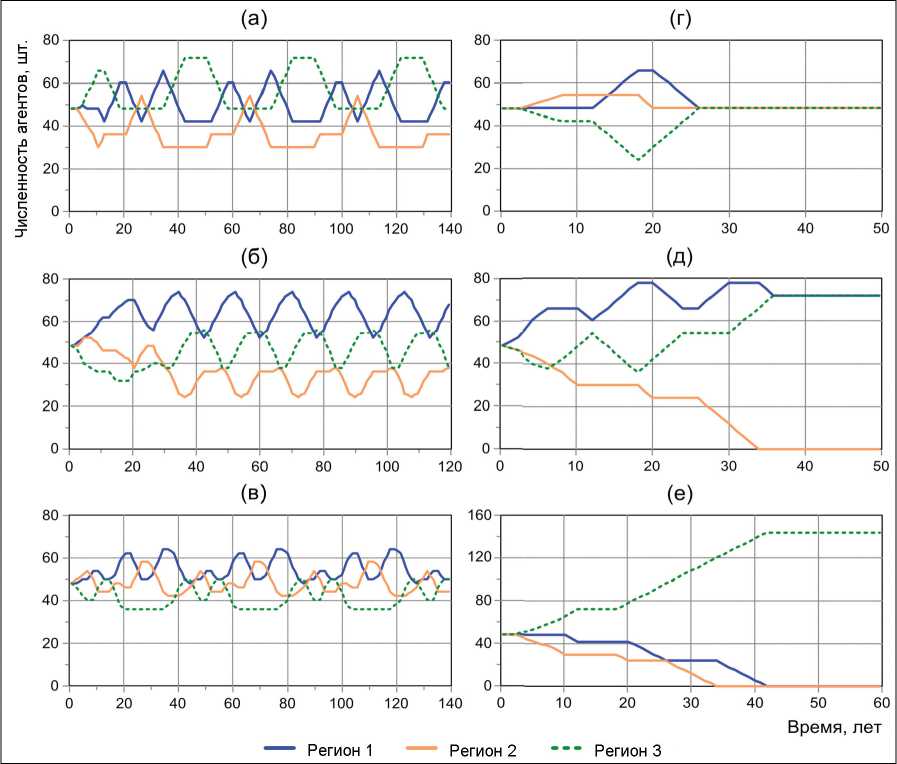
Рис. 2. Динамика численности населения в трех модельных регионах при замещении 63-летних агентов на агентов различных возрастных групп: а) 24-летних во всех трех регионах; б) 36-, 34-, 46-летних в первом, втором и третьем регионах соответственно;

в) 16-, 24-, 22-летних в первом, втором и третьем регионах соответственно; г, д, е) 40-, 52- и 56-летних во всех трех регионах

• Fig. 2.    Population dynamics in three model regions when replacing 63-year-old agents with agents of different age groups: a) 24-year-olds in all three regions; b) 36-, 34-, 46-year-olds in the fi rst, second and third regions respectively; c) 16-, 24-, 22- in the fi rst, second and third regions respectively; d, e, f) 40-, 52- and 56-year olds in all three regions

  
  
  

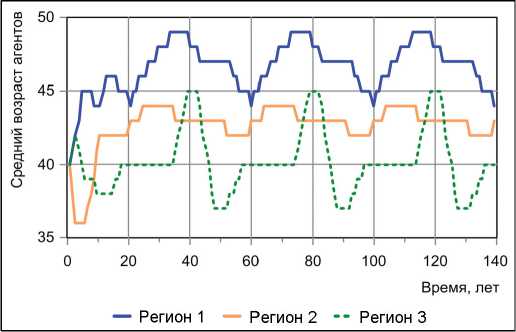
Рис. 3. Динамика среднего возраста агентов по регионам в модели при замещении 63-летних агентов на 24-, 16-, 24-летних мигрантов в первом, втором и третьем регионах соответственно

• Fig. 3.    Dynamics of the average age of agents by regions in the model when replacing 63-year-old agents with 24-, 16-, 24-year-old migrants in the fi rst, second and third regions respectively

Заключение

Таким образом, результаты моделирования позволяют утверждать, что наличие различных стратегий выбора мигрантами региона в совокупности даже с линейным изменением возрастной структуры в регионах действительно может вызывать перераспределение численности населения, приводящее к периодическим режимам динамики. При этом отсутствие в модели экзогенных факторов в виде экономических циклов (и в этом смысле ее «рафинированность») ясно демонстрирует эндогенный характер колебаний. Результаты данного исследования качественно объясняют отсутствие в ряде случаев значимой корреляции между социально-экономической динамикой и миграцией.

Исходя из полученных результатов, также можно утверждать, что игнорирование учета стратегий миграционного поведения приводит к безре-зультативной миграционной политике. Например, программа по переселению соотечественников никак не повлияла на сокращение численности населения Дальнего Востока [5].

Дальнейшее развитие настоящего исследования может заключаться в изучении, с одной стороны, сложных режимов динамики численности мигрантов, исходя из стратегий миграционного поведения, с другой стороны, в дальнейшей детализации модели для прогнозирования демографической динамики на региональном уровне.

Работа выполнена при финансовой поддержке РФФИ, проект № 19-010-00206.