Моделирование петрографических структур

Структура и текстура — атрибуты любой горной породы, содержащие разнородную информацию о ее генезисе. Петрографические словари определяют их как совокупные характеристики форм (панидио-, гипи-дио- и ксеноморфно-зернистые структуры), абсолютных и относительных размеров (тонко-, мелко-, средне- и крупно-, равномерно- и неравномерно-зернистые, порфировидные и порфировые структуры) слагающих горную породу минеральных зерен, а также пространственных отношений их самих (пойкилитовая структура) и агрегатов (массивная, шлировая, полосчатая текстуры) [5]. Отдавая должное поколениям петрографов, описавших сотни структур и текстур, заметим, что они не укладываются в математическую систему не столько из-за разнообразия, сколько из-за намерения вместить в одну характеристику несколько разнородных измеримых параметров и даже генетические (!) представления. Типичный пример — лепидогранобласто-вая структура, указывающая на чешуйки слюды, изо- метричные зерна кварца и бластез горной породы. Мы видим в этом недостаток сегодняшней петрографической номенклатуры. (Можно ли представить номенклатуру точечных или пространственных групп симметрии, в которую входили бы утверждения о генезисе измеряемых кристаллов?) Тем не менее подчеркнем, что дальнейшие подходы предлагаются в дополнение, а не вместо существующих.

Принципы моделирования

Всякая модель представляет объект лишь в тех аспектах, которые полагаются всеобщими и принципиальными. Все более полное описание достигается пошаговым добавлением в модель более частных аспектов. В этом исследовании мы руководствовались следующими принципами.

Номенклатура петрографических структур и текстур сложилась при их наблюдении в 2D-поверхностях: обнажениях, штуфах, шлифах под микроскопом. Моделирование в 3D привело бы к сложной пробле-

ме стереологической реконструкции, то есть распознаванию в сечениях. Поэтому моделирование выполнялось сразу в 2D.

Горная порода — системный объект с определенными элементами (минеральными зернами различных видов) и пространственными отношениями (контак-тирования/неконтактирования). Сложность системы более зависит от специфики отношений, чем от разнообразия элементов (хотя ясно, что отношений без элементов не бывает). В этом исследовании мы избегаем описания элементов (форм и размеров минеральных зерен) и делаем акцент на описании их отношений контактирования.

Диагностика минеральных видов и характеристика форм и размеров минеральных индивидов — минералогический, а не петрографический уровень исследования. Последний состоит в узнавании горной породы по ее модальному составу (из которого следует химический состав, а если не следует, то потому, что составы минералов варьируют в широких пределах) и типу организации (структуре и текстуре), что в обоих аспектах подразумевает статистический подход.

Статистический подход содержится и в традиционном описании горной породы, ведь мы всегда отбираем «представительный» штуф, в котором достигается ее узнаваемый облик. В этом исследовании для характеристики пространственных отношений минеральных зерен мы используюем вероятности бинарных контактов. Моделирование выполнено для бими-неральной горной породы. В этом простейшем случае вероятности контактов и расчетные тренды можно изобразить в барицентрической диаграмме {p_ii, p jj , p ij }. Возможности моделирования полиминеральных структур обсуждены отдельно.

Принципиально важная черта организации горных пород (а также металлов и сплавов) состоит в том, что 4 зерна контактируют в точке, 3 — по линейному ребру, 2 — по некоторой поверхности [1; 6, с. 34—35]. В случайное сечение первые не попадают, вторые выглядят как тройные контакты в точке, последние — как бинарные контакты вдоль линии (рис. 1). Но для любого планарного графа выполняется соотношение Эйлера: n — e + v = 1, где n — число клеток, e — ребер, v — вершин. В нашем случае (представляя граф без края — так мыслится и кристаллическая решетка) 3v = 2e. Тогда e = 3n — 3 « 3n при n ^ да. Средняя координация клетки: 2e / n = 6 — 6/n ^ 6 при n ^ да.

Поэтому статистическое моделирование петрографических структур возможно на гексагональной сетке (рис. 1). На первый взгляд, это противоречит сказан ному выше об игнорировании форм минеральных зерен. Но для дальнейшего важны не гексагоны (их можно заменить точками в центрах), а усредненные характеристики сетки: общее число бинарных контактов 3n и средняя координация клетки 6. Историческая аналогия — переход О. Браве от форм «полиэдрических молекул» P.-Ж. Гаюи к размещению в пространстве их центров, что привело к открытию 14 типов решеток. Удивительно, что правильное кристаллографическое разбиение плоскости на гексагоны проявилось «в среднем» в неправильном рисунке межзерновых границ в сечении горной породы.

Вкрапленные структуры, массивные текстуры

Пусть n — общее число минеральных зерен, тогда 3n — общее число бинарных контактов в структуре. Пусть kn — число черных зерен, рассеянных в белой матрице, здесь и далее 0 < k < 1 (оценка точной верхней границы для k всякий раз составляет задачу). Тогда числа различных бинарных контактов равны: Nчч = 0, Nчб = 6kn, N66 = 3n — 6kn. Делением на 3n найдем соответствующие вероятности: рчч = 0, рчб = 2k, рбб = 1 — 2k. Предположительно, максимальная концентрация черных зерен достигается для k = % (рис. 2). Серия вкрапленных структур для 0 < k < % образует ограниченный непрерывный тренд на ребре (рбб, рчб) барицентрической диаграммы (рис. 3). Равномерное рассеяние черных зерен среди белых создает массивную текстуру.

Пойкилитовые структуры

Пусть n — общее число ойкокристаллов, m — хадакристаллов (рис. 2). Общее число контактов: Nчч = 0, Nчб = m, N66 = 3n. Соответствующие вероятности: рчч = 0, рчб = m/(3n+m) = 1/(1+3n/m), рбб = 3n/(3n+m) = 1/(1+m/3n). Если хадакристаллов относительно мало, т. е. m/3n ^ 0, то рчб ^ 0, рбб ^ 1. Если хадакристаллов относительно много, т. е. 3n/m ^ 0, то рчб ^ 1, рбб ^ 0. Тренд пойкилитовых структур занимает все ребро (рбб, рчб) барицентрической диаграммы (рис. 3).

Цепочечные структуры, полосчатые текстуры

Пусть n — общее число минеральных зерен, тогда 3n — общее число бинарных контактов в структуре. Пусть kn — число черных зерен в цепочках. Тогда Nчч = kn, Nчб = 4kn, N66 = 3n — 5kn. Соответствующие

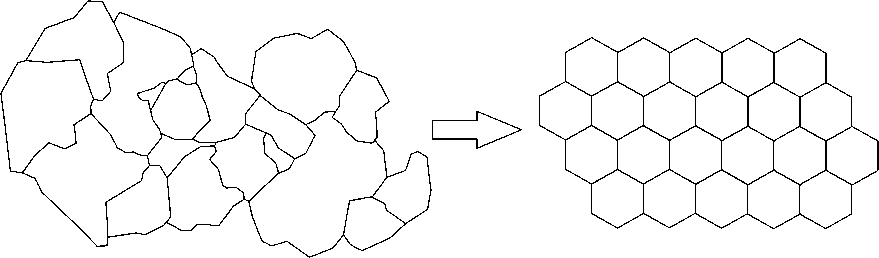
Рис. 1. Межзерновые границы в петрографическом шлифе и гексагональная сетка

Fig. 1. Intergranular boundaries in a petrographic section and a hexagonal net

Рис. 2. Модели структур и текстур: 1 — вкрапленная, 2 — пойкилитовая, 3 — цепочечная, 4 — с ветвящимися кластерами, 5 — шлировая, 6 — порфировая

Fig. 2. The models of the structures and textures: 1 — disseminated, 2 — poikilitic, 3 — chained, 4 — with branching clusters, 5 — schlieren, 6 — porphyric

вероятности: pчч = k/3, pчб = 4k/3, p66 = 1 — 5k/3. Предположительно, максимальная концентрация черных зерен достигается для k = ^ (рис. 2). Серия цепочечных структур для диапазона 0 < k < % образует непрерывный тренд (рис. 3). Превращением цепочек в черные полосы и варьированием (через k) ширины белых полос между ними моделируются полосчатые текстуры. Их тренды покрывают угол барицентрической диаграммы ниже тренда цепочечной структуры.

Структуры с ветвящимися кластерами

В работе [2, с. 10—13] описаны структуры с ветвящимися кластерами зерен кварца в полевошпатовой матрице. Выполним моделирование для кластеров из 7 зерен (рис. 2). Пусть n — общее число минеральных зерен в структуре, тогда 3n — общее число бинарных контактов. Пусть kn — общее число кварцевых зерен в кластерах. Тогда число кластеров равно kn/7. Число контактов: N_чч = kn, N_чб = 4kn, N₆₆ = 3n — 5kn. Соответствующие вероятности: p_чч = k/3, p_чб = 4k/3, p ₆₆ = 1 - 5k/3. Результат совпал с предыдущим, так как цепочки и ветвящиеся кластеры отличаются лишь одним зерном — центром ветвления, что не сказалось на статистике контактов.

Шлировые текстуры

Пусть n — общее число минеральных зерен, тогда 3n — общее число бинарных контактов в структуре. Пусть kn — число зерен, собранных в шлиры по 7 40

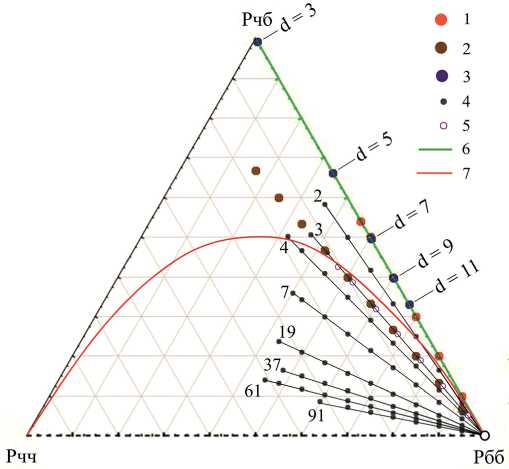
Рис. 3. Барицентрическая диаграмма вероятностей (p ii , p jj , p ij ). Структуры и текстуры: 1 — вкрапленная, 2 — цепочечная, 3 — порфировые (d — диаметр фенокриста), 4 — шлировые (количества зерен в шлирах указаны числами), 5 — с ветвящимися кластерами, 6 — пойкилитовые; 7 — линия равновесия Харди — Вайнберга

Fig. 3. Barycentric diagram of (p ii , p jj , p^) probabilities. Structures and textures: 1 — disseminated, 2 — chained, 3 — porphyric (d — diameter of phenocryst), 4 — schlieren (quantities of grains in the schlierens are indicated by the numbers), 5 — with brunching clusters, 6 — poikilitic; 7 — the Hardy—Weinberg equilibrium line

(рис. 2). Тогда число шлиров в структуре kn/7, число контактов: Nчч = 12kn/7, Nчб = 18kn/7, N66 = 3n — 30kn/7, соответствующие вероятности: рчч = 4k/7, рчб = 6k/7, рбб = 1 — 10k/7. Тренды шлировых текстур для разных размеров шлиров и значений k покрывают барицентрическую диаграмму ниже тренда цепочечной структуры (рис. 3).

Порфировидные и порфировые структуры

Эти структуры удобно моделировать как предыдущие, у которых в шлирах стерты межзерновые границы. Характеристика модельных шлиров дана в таблице. Здесь d — диаметр шлира (диаметр белого зерна принят за 1), n(d) — число зерен в шлире (аппроксимируется величиной nd²/4), v(d) = N_чч — число границ в шлире, p(d) = N_ч б = 6d — число внешних границ шлира, 2 = N^ + N чб /2 = 3n(d).

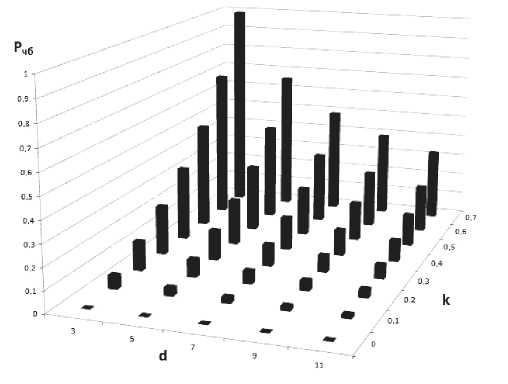
Рис. 4. Соотношение d и k для порфировых структур

Fig. 4. Relationship between d and k for рогрКупс structures

Характеристика модельных шлиров Characteristics of model shlierens

d	3	5	7	9	11
n(d)	7	19	37	61	91
v(d)	12	42	90	156	240
Р(d)	18	30	42	54	66
Σ	21	57	111	183	273

Пусть n — общее число минеральных зерен, тогда 3n — общее число бинарных контактов в структуре. Пусть kn — число зерен в шлирах, тогда 3kn — числа контактов в kn/n(d)-шлирах. Стирая внутренние границы, превратим шлиры в порфировые вкрапленники. Число оставшихся контактов: Nчч = 0, N66 = 3n — 3kn — knp(d) / 2n(d) = 3n(1—k) — 12kn / nd, Nчб = 2knp(d) / 3n(d) = 16kn / nd. Деля на их сумму, получим вероятности: рчч = 0, рчб = 16k/ [3nd(1-k) + 4k], рбб = 1 — рчб.

Тренды порфировидных и порфировых структур в совокупности покрывают ребро (р бб , р_ч б ) барицентрической диаграммы (рис. 3). Каждый начинается вблизи вершины р_бб и простирается к вершине р_чб тем далее, чем меньше диаметр кластера. При фиксированном d предельное значение k вычисляется из условия Р_чб > 0 (рис. 4).

Обсуждение и выводы

Выше предложена барицентрическая диаграмма нового типа, показывающая вероятности бинарных межзерновых контактов (в простейшем случае бими-неральной горной породы), существующих во всех кристаллических горных породах и тем самым выражающих фундаментальные пространственные отношения между слагающими их минеральными индивидами. При заданном виде кластера моделируются любые петрографические структуры и текстуры. При этом их канонические типы закономерно заполняют поле диаграммы трендами, определяемыми видом кластера и его концентрацией в структуре. (Левая часть диаграммы на рис. 3 симметрично заполняется структурами «белые кластеры в черной матрице».) Фигуративные точки реальных петрографических структур и текстур должны занимать промежуточные положения между модельными трендами.

Около вершины р_ч б внутри диаграммы есть поле, в которое модельные тренды не проникают. Это означает, что невозможна петрографическая структура без мономинеральных контактов (типа шахматной доски), образуемых хотя бы одним минералом (таковы модельные вкрапленные и пойкилитовые структуры). В реальных петрографических структурах обычны мономине-ральные контакты обоих видов. Для расчетных трендов могут быть оценены предельные точки, вместе ограничивающие запрещенное поле.

Тренды различных структур (например, цепочечной и с ветвящимися кластерами) и поля текстур (полосчатых и шлировых) в поле диаграммы перекрываются. Совпадение статистик бинарных контактов и, как следствие, термодинамических характеристик [3] сети межзерновых границ обращает внимание на фундаментальный вопрос: почему горная порода следует той или иной стратегии кристаллизации, приводящей к той или иной структуре?

Интересен вопрос о соотношении различных структур и текстур с рассмотренным ранее [4] равновесием Харди — Вайнберга, выражающим гомогенное перемешивание минеральных индивидов в горной породе (массивная текстура). На диаграмме видно, что тренды вкрапленных, пойкилитовых и цепочечных структур, начинаясь вблизи вершины рбб диаграммы, на значительном протяжении следуют вблизи линии равновесия. Явно отклоняются от нее ярко выраженные порфировые, пойкилитовые и цепочечные структуры, а также полосчатые и шлировые текстуры.

Возможно ли расширение метода на полимине-ральные структуры? Принципиальных препятствий к этому нет. Проблема состоит в визуализации барицентрических диаграмм и поверхностей равновесия Харди — Вайнберга. Даже для трехминеральной горной породы это 2-мерная поверхность в 6-вершинном (5-мерном) симплексе. В этом случае более наглядно последовательное рассмотрение полиминеральной структуры в виде «минерал — матрица» для каждого из слагающих горную породу минералов и сравнение результатов на барицентрической диаграмме.

Расчет вероятностей бинарных межзерновых контактов — рутинная процедура даже для биминеральной горной породы. Мы изучаем возможность применения для этих целей линейного метода Розиваля в компьютерном варианте и с применением отечественного анализатора структуры МИУ-5.