Моделирование пищевой безопасности

Ввдение

Некоторые явления в пищевой безопосности вынуждают качественный подход глубокого изучения поведения химических и микробных контаминантов в ПП. Математические модели могут быть полезним инструментом в реализации данного изучения. В данной статье рассматривается применение математических моделей, описывающих поведение контаминантов в двух направлениях: 1) вероятностная микробиология и 2) миграция химических соединений из упаковочных материалов. Математический подход для оценки риска обсуждается также. Одноко, целыю статьи не является загружать читателя математическими уравнениями. Уравнения приводятся лишь для иллюстрации различных подходов, применяемых для освещения вышеотмеченной задачи.

Резултаты и их обсуждение

• I.    Вероятностная микробиология-моделирование поведения микроба.

За последние деятелетия диоксины и ПХБ, а также микробные опасности, тикие как листерия и бациллис достигли значительное распространение и стали критическими для здоровья потребителя. Вероятностная микробиология может рещить эти проблемы. Разработанная модель даст возможность быстрого способа оценки сроков хранения в соответсвии с микробным повреждением и оценить микробную безопасность ПП. Такая информация можеть быть применима для различных условий хранения и способствует принять коррективные меры. Более того, возможности IT возросли экспоненциально, цены упали, сделав возможным для каждого пользователя доступ к появляющимся методологиям моделирования.

Вероятностной пищевой микробиологии можно дать такое опроделение, как применение математических выражений для описания поведения микробов в ПП.[1] она основывается на допушение, что отношения рассматриваемый популяция микроорганизмов к факторам внешней среды воспроизводима и, что характеризуя окружающую среду, исходя из тех факторов, которые наиболее сильно подавляют рост и появление микроорганизмов, вожможно из последного наблюдения, чтобы предсказать отношение этих микробов к другой, схожей окружающей среде[2]. Эти знания можно описать и суммировать математической моделью, которая может быть использована для предсказания количественного поведения популящи микробов ПП, т.е. рост, вымирание образование токсинов по навыкам окружающей ПП среды за все время.

Классически, модели могут быть разделены на 3 группы: начальная модель описывающая эволюцию во времени количества бактерий в заданных, установленных условиях. Когда эти условия блогоприятны для бактерий 1-я модель будет моделью роста, в то время как в условиях стресса, это модель будет моделью инактивации. 2-я модель занимается влиянием условый окружающей среды, как Т,РН, aw или состав атмосферы, на 1-ю модель. В 3-й модели предыдущие два суммируются и применяются осторожном (бережном) упаковывание. В данной статье будут суммированы текушие инструменты моделирования: будут обсуждаться различные типы 1-й и 2-й модели (некоторые), освещаются процедуры разработки модели и приводятся некоторые показательные примеры.

Совсем недавно разработана вероятностная модель для роста бактерий в специалных условиях окружающей среды, т.е. при наличии ряда стрессов, которые в отдельности не влияют, но вместе подавляют рост[2]. Эти модели, также названные моделями «рост/ нет роста» интерфейсными моделями, освещают переход между моделю роста и моделью инактивации.

Предполагается, что традиционное разделение вероятностной микробиология на кинетические и вероятностние моделе является искусственным. Они аргументируют, что 2 типа модельного подхода представляют удобнем окончания спектра требований моделирования, с исследованием обоих концов случайно сходящимся вместе это может быть доказано моделями «рост/ нет роста», который является логическим продолжением модели кинетики роста. Когда окружающие условия становятся более стрессными, скорость роста медленно падает, лаг-фаза продолжается до тех пор, пока скорость роста не станет равной нулью, или лаг-фаза достигнет вечно. В пределах сумерный зоны моделирование нуждается в смещении от кинетической модели, когда окружающие условия все ешё поддерживают рост, к вероятностной модели, когда достигается интерфейс «рост/ нет роста», демонстрируя тесную связь между 2 типами моделей.

Обычно используется для моделирования роста клеток как функция времен кривая сигмондного роста, хотя иногда кримлияется 3-хфазная липейная модель в качестве укрощения[5]. Пример приведен на рис.9.2. символы показывают собранным данные, в то время как сплошная линия представляет модель сигмондного роста. Кривые роста в основном чертяте на основанной шкале для плотности клеток как функцию времени, т.к. рост микробов является экспоненциальным феноменом, но иногда предпочитается база натурального логаризма ln.

Традиционно, кривая сигмондного роста описивается, используя 4 параметра скорость экспоненциального роста µ мах , лаг-фаза уровень инокулума и максимум плотности клеток N max . Скорость экспоненциального роста определяется как крутая касательной к экспоненциальной фазе, так тангенс точки прилипание, в то время как лаг-фаза определяется как время в течении которого экстрополированная касательная линия пересекает уровен инокулума [5]. Время генерации (GT) , время необходимое для удвоения клеток в час или день, может быть рассчитан из µ_max:

Мщах О

В 80-х годох была предложена нелинейная модели. Гибсон с сотр.[3] ввели функцию Гомерца в пищевую микробиологию, делая её способным выражать log(cfu/мл)как функцию времени, используя сигмоидную форму.

logN(t)=A+Dexp{exp[-B (-ЛОВ , где

^ -плотность клеток по времени 1

£ значения нижней асимитоты разность значения между верхней и нижней асимитотойNmax-No

• -^J -время, при котором скорость роста является максимальной

• - -относится к скорости роста

Параметри модели Гомперц могут быть преоброзованы в характеристику классической первычной кривой роста

N о =А

Nmax=A+D pmax=BD/exp(1)

Х=М*1/В

В соответствии с моделью Гомперц Гибсоном была предложена логарифмическая сигмоидная кривая для предсказания роста бактерий

D lo g N (t)=-------------------

А + exp[-B(t-M)]

Полученные результаты схожи с функцией Гомперца, но логарифмеческая модель является симметричной моделью, в то время как кривые роста-нет. Поэтому модель Гомперца была предпочтительной, чем логорифмическая модель. В раннех исследованиях точка знания двигалась от статической 1-й модели к динамической 1-й модели. Предполагалось [6], что динамическое дифференциальное уравнения 1-го порядка для предсказания как роста микробов, так и их инактивации по отношению к времени и к температуре. Она была одной из 1-х разработанных моделей, которая была способна учитывать изменяющуюся во времени температуру всей температурной области роста и инактивации. Также можно было иметь ввиду предыдущую историю продукта. В специальных случаях постоянства температуры модель ведет себя подобно соответствующей модели Гомперца.

2-я модель динамического роста была разработана[7] и она основывается на диференциальном уравнение 1 -го порядка.

dx

d: = - ' "'   , где x(t)-концентрация клеток при времени t, - ' ''-скорость специального роста. Если p(x)=pmax= то уравнение описывает чистый экспоненциальный рост.

Дифференциальное уравнение 1-го порядка сводится к двум корректированным функциям: адаптация функции a (t), описывающая гладкий переход от уровня инокулума к экспоненциальной фазе роста, и функция ингибирования u(x), описывающая переход от экспоненциальной фазы роста к стационарной фазе. Поэтому структурой для модели роста является:

d x /d t =p max a(t) и (х)х

Вторичные модели

2-е модели моделируют влияние внутренных (pH, a w и др.) и внешных (T,P,C и др.) факторов на рост микроорганизмов внутри матрикса ПП. Были построены различнем моделным подходы, простирающие от полностыю эмпирических моделей к более механистически ориентированные попытки со множеством переменных в формуле модели. Примерами могут быть 4 группы моделей: 1)модель Аррениуса и её модификации, 2)модель Белерадека или квадратный корень модели, 3)модель кардинальных значений, 4)модели зависимости от поверхности[8] или полиномалны модели.

Третычные модели

Наиболее хорошо известными 3-ми моделями являются PMP-pathogen modelling programm, который разрабатывался(USDA) PMP= ПМП-потоген US Drug модулирующим администрация программы. Она описывает поведение различных патогенных бактерий как функцию условий окружающей среды. Модель содержий кривую роста, кривую инактивации, наблюдение, охлаждение и модели облучения. Модель регулярно обогащается текущими знаниями по моделированию. РМР можно скачать из вебсайта USDA.

Другой хорошо известной программой является предсказывание повреждения морские пищевых продуктов (SSP-Seafood Spoilage Predictor), который фокусирован на порчу морской свежей рыбы, как функцию температуры и газовой среды. Реалистическая комбинация время-температура может быть определена и будет предсказан последующий рост бактерий, вместе с оставшиеся срок хранени ям. Программу можно легко скачать из интернета.

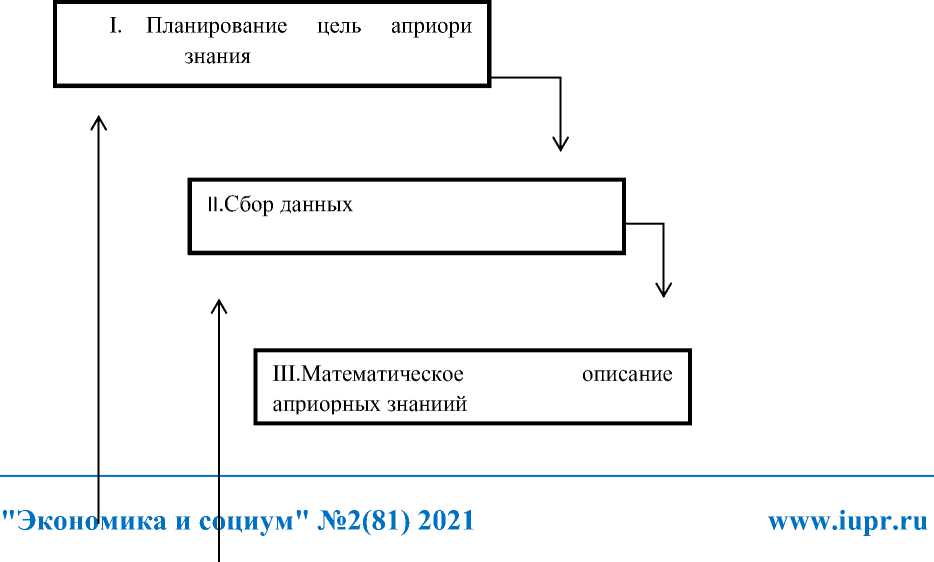
Разработка предсказывающей модели в области пищевой безопасности в основном осуществляется в 4 стадии: 1) планирования 2) сборданных и анализ 3) пример функции 4) проверка и поддержка (рис1):

Модельный цикл

енен ие

• IV. Достоверность модели

  

Вероятностная микробиология нацелене на количественный расчет роста микробов в ПП, с применением математического моделирования. Для определения того, что предположение предоставляет хорошое совпадения описания роста микробов в ПП. Модель должен быть проверен по предсказывающей способностью[9]. Проверку следовало бы проводить в питательной среде, но особенко лучше в реальном ПП.

Точность модели можно оценить графически, откладывая наблюденные значения против соответствующих значений вероятностной модели. Более того, среднеквадратичную (MSE) ошибку и значения R* также можно использовать в качестве индикации достоверности модели, когда она применяется для ПП. Росс(10) предложил указания по возможностям математических моделей, используемых в вероятносной микробиологии. Цель этих указаний заключалась в способности оценить достоверность таких моделей, когда они сравниваются с наблюденными, не использиванные для генерации модели, особенно в ПП, и следовательно оценить их utility помочь в решениях по качеству и безопасноста ПП. Дальнийшая цель заключалась в предоставлении простых и количественных измерений достоверности модели.

Заключение

Применение вероятностных моделей может быстро предоставляеть информацию и поэтому, является важный для ценить реальное значения и полезность предсказывающих моделей. Однако, важно подчеркнуть, что их применения не сможет полностью заменить микробный анализ образца или значения технических навыков и работу опытного микробиолога. Это можно описать следующим образом:  модель является хорощим дискусионным партнером, дающим вам хорошую идею, указывая вам правильное направления, но подобно другим дискуссионным партнеромбывает не всегда прав. Она должна рассматриваться как один из инструментов, который дает решение, активный в сфере ПП, имеет свои позиции для консолидации их решений. (в табл. суммированы многие применения, предложенные для вероятностной пищевой микробиологии)

Абстракт (Резюме)

В статье приводится обзор литературных данных и сообственные суждения по вопросом математического моделирования качестве и безопосности ПП. За основу взят поведение микроорганизмов в различных условиях хранения и переработки сырья и продукции агропроизводства. Рассматриваются такжее условия и сферы применения различных типов (1-х,2-х,3-х) моделей вероятностной микробиологии.

Табл1:  Возможные сферы применении вероятностной пищевой микробиологии

• I.    Анализ опасности и конгтроль крит.точек(НАССР)

• 1.    Предворительный анализ опасности

• 2.    Идентификация и установление критических контролных точек

• 3.    Корректирующии действия

• 4.    Оценка значений взаимодействие между переменными

• II.    Оценка риска

• 1.    Оценка изменения числа микробов в цени производства

• 2.    Оценка экспозиции к определенному патогену

• III.    Изучения условий жизни микробов

• 1.    Предсказание роста специальных вредителей ПП.

• 2.    Предсказание роста специальных потогенов в ПП.

• IV.    Исследование и разработка продукта

• 1.    Эффект изменения состава ПП на пищевую безопосность и порчу ПП.

• 2.    Влияние переработки на пищевую безопосность и порчу ПП.

• 3.    Оценка влияния отклонений от специфических обстоятельств V. Интегральная функция температуры и активные гигиенические дейсвия

• 1.    Температурные последствия в цени охлаждения на безопосности и порчи ПП

• VI.    Обучение

• 1 .Обучение технического и особенно не технического персонала

• VII.    Дизайн опытов

• 1.    Число образцов, которые необходымо приготовить

• 2.    Определение интервала между взятием проб.