Моделирование пятиярусных конструкций в виде гиперболоидов вращения и проведение лабораторных испытаний по изучению изменений нагрузок на узловые крепления

В 1919 г. В.Г. Шухов создал проект огромной 160-метровой гиперболоидной радиобашни – именно она возвышается сегодня на Шаболовке [1]. Следует отметить, что данный проект был не свойственный для той эпохи, если говорить о габаритах объекта [2].

Башня на Шаболовке состоит из шести ярусов (высота каждого – 25 м). Каждый ярус представляет собой гиперболоид вращения – объемную конструкцию из прямых стальных балок, концы которых скреплены стальными кольцами и заклепками [3].

Первый ярус опирается на бетонный фундамент, диаметр которого 40 м, а глубина 3 м. Башня строилась без использования строительных лесов или подъемных кранов. Возведение происходило следующим образом: каждый следующий ярус собирался внутри башни, а затем с помощью блоков и лебедок поднимался наверх. То есть башня вырастала телескопически [4].

Легендарный проект В.Г. Шухова совсем скоро приобрел огромную популярность, прославился на всю страну, и вскоре после этого сетчатые стальные оболочки в виде гиперболоидов вращения начали массово применяться и по всему миру. За прошедшие 100 лет в мире построено несколько десятков высотных гиперболоидных башен. К ним можно отнести 600-метровую телебашню в Китае [5].

Гиперболоидная конструкция оказалась очень экономичной с точки зрения металлоемкости, но при этом достаточно прочной. А ее ажурность позволяет эффективно противостоять ветровой нагрузке, главному врагу высотных сооружений. Элементы конструкции довольно просты в производстве и строительстве, следовательно, стоимость их невысокая [6].

Конструкция башни состоит из прямых металлических балок и кольцевых опор, которые довольно просты и недороги в изготовлении. Узловые соединения также имеют простую конфигурацию [7].

В частности, использовались упрощенные модели распределения нагрузок, не учитывался ряд характерных особенностей вроде скручивания опорных колец, закрутки балок и продольные деформации. Тем не менее проведенные в последующие десятилетия исследования прочности Шухов-ской башни, в которых применялись более совершенные и точные методики расчета, показали результаты, близкие к расчетам самого Шухова [8].

Эксперимент

Моделирование пятиярусных конструкций в виде гиперболоидов вращения и проведение лабораторных испытаний по изучению изменений нагрузок на узловые крепления были выполнены физически на кафедре «Промышленное и гражданское строительство» Рязанского института (филиала) ФГАОУ ВО «Московский политехнический университет».

Конструкция самого гиперболоида вращения создавалась из полимерных материалов длиной 80 мм, шириной 10 мм. Данный материал имел внутри 13 равноудаленных друг от друга отверстий диаметром 4 мм. Данные полимерные материалы соединялись между собой болтами, гайками и шайбами с двух сторон. Элемент данного соединения изображен на рис. 1.

Для исследования была создана инженерная конструкция, состоящая из гладкой и прямой деревянной основы из фанеры толщиной 10 мм. Площадь конструкции составила 0,85 м2.

Далее в данный подиум было вмонтировано деревянное основание для вертикальной металлической опоры. Размер основания составил 50 × 50 мм. Основание было прикреплено к подиуму 4 саморезами длиной 4 × 40 мм. Это дало достаточно прочную основу для конструкции. Одним из вариантов нагружения могло быть отверстие диаметром 6 мм в деревянном основании, через которое проходил металлический стержень диаметром 4 мм, длиной 600 мм, на который подвешивались грузы. Однако в качестве основного вида нагружения использовалась схема с верхним нагружением, когда грузы устанавливались непосредственно на верхнюю распределительно-нагрузочную крышку.

На уровне 450 мм от уровня подиума из двух деревянных брусков путем соединения 4 болтами и гайками был сформирован вспомогательный элемент для фиксации индикаторной головки часового типа. Элемент одной стороной крепился болтами к металлической части прута с помощью стягивания болтов, другая же сторона находилась в свободном, подвешенном горизонтально относительно плоскости подиума уровне. На этой части с помощью болтов была зафиксирована индикаторная головка часового типа (рис. 2), направленная вертикально.

Рис. 1. Элементы для формирования пояса параболической поверхности:

а – одинарный крест для формирования образующей поверхности; б – двойной крест для формирования образующей поверхности; в – тройной крест для формирования образующей поверхности.

Серым цветом обозначены места соединений

Индикаторная головка соприкасалась с контрольным винтом, находящимся на верхнем ярусе башни с целью измерения изменения нагрузок гиперболоида в зависимости от экспериментируе-мого веса.

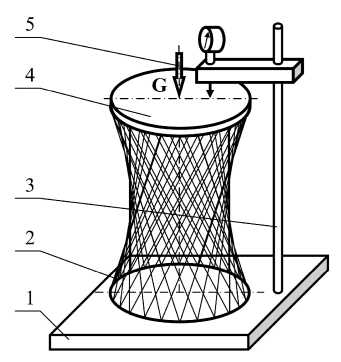
Рис. 2. Общий вид установки для определения деформаций: 1 – станина;

2 – модель пятиступенчатого гиперболоида;

3 – вертикальная стойка с индикаторной головкой;

4 – верхняя распределительно-нагрузочная крышка;

5 – грузы весом G

Для увеличения нагрузки на гиперболоид использовались металлические грузы весом 1 кг (9,80 Н). Располагались они строго перпендикулярно на верхнем ярусе башни. Первоначально располагался 1 груз, фиксировались показания нагрузок на узловых креплениях. Затем к первому грузу добавлялся 2-й груз (2 кг, 19,6 Н), фиксировались показания, затем к двум грузам добавлялся третий (3 кг, 29,4 Н), показания также фиксировались. Также до добавления первого груза фиксировались нулевые показания.

В первом эксперименте мы установили башню с пятью ярусами по 20 полимерных элементов в каждом ярусе, соединенных болтами. Затем нагрузка была постепенно увеличена с 0 до 3 кг (29,4 Н). Результаты изменения деформации представлены в табл. 1.

Из полученных результатов видно, что при увеличении нагрузки с 1 кг (9,80 Н) до 3 кг (29,4 Н) разница в деформации конструкции в узловых соединениях увеличилась на 0,33 мм.

Деформация пятиступенчатого образца от нагрузки с 20 точками двойного схождения показана на графике (рис. 3).

Во втором эксперименте на станину стенда была установлена пятиступенчатая модель гиперболоида с 22 полимерными элементами в каждом ярусе, с точечным соединением болтами. Нагрузка была осуществлена ступенчатым увеличением с 0 до 3 кг (29,4 Н). Результаты изменения деформации представлены в табл. 2.

Таблица 1

Деформация пятиступенчатого образца с 20 точками двойного схождения

Показание индикатора	Деформация пятиступенчатого образца от нагрузки, мм
	0 нагрузка	1 кг (один груз)	2 кг (два груза)	3 кг (три груза)
Начальное	0,60	0,79	0,98	0,12
Текущее		0,19	0,19	0,14
Суммарное		0,19	0,38	0,52

Таблица 2

Деформация пятиступенчатого образца с 22 точками двойного схождения

Показание индикатора	Деформация пятиступенчатого образца от нагрузки, мм
	0 нагрузка	1 кг (один груз)	2 кг (два груза)	3 кг (три груза)
Начальное	0,86	0,62	0,34	0,2
Текущее		0,16	0,18	0,32
Суммарное		0,16	0,34	0,66

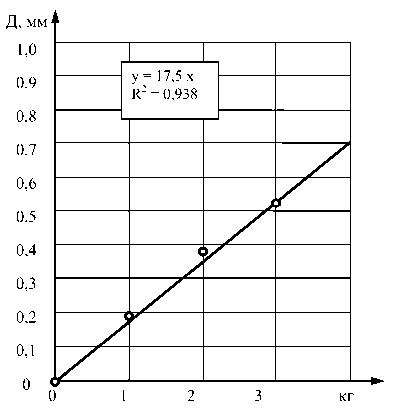
Рис. 3. Деформация пятиступенчатого образца от нагрузки с 20 точками двойного схождения

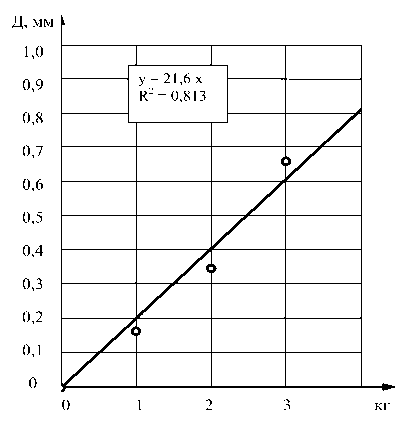
Рис. 4. Деформация пятиступенчатого образца от нагрузки с 22 точками двойного схождения

По результатам исследований видно, что при увеличении нагрузки с 1 кг (9,80 Н) до 3 кг (29,4 Н) разница в деформации увеличилась на 0,50 мм. Такая разница в деформации свидетельствует о снижении жёсткости с увеличением диаметра модели гиперболоида.

Деформация пятиступенчатого образца от нагрузки с 22 точками двойного схождения показана на графике (рис. 4).

В третьем эксперименте на станину был установлен гиперболоид с пятью ярусами по 24 полимерных элемента в каждом ярусе, соединенных болтами. Нагрузка также увеличивалась ступенчато с 0 до 3 кг (29,4 Н). Результаты изменения деформации представлены в табл. 3.

Из табл. 3 и на рис. 5 видно, что при увеличении нагрузки с 1 кг (9,80 Н) до 3 кг (29,4 Н) деформация увеличились на 0,58 мм. Данные показания в деформации ещё раз подтверждают то, что с увеличением диаметра гиперболоида при постоянной высоте их жёсткость снижается, а деформация увеличивается.

Деформация пятиступенчатого образца от нагрузки с 24 точками двойного схождения показана на графике (рис. 5).

Общие деформации и изменения нагрузки на узловые крепления пятиступенчатых гиперболоидов представлены на рис. 6.

Выводы

При проектировании конструкций зданий в виде гиперболоидов вращения в архитектуре используются различные законы математики, физики, сопротивления материалов и строительной механики [9]. Важнейшими из них являются законы Ньютона и Гука. Они тесно связаны с силами, которые опираются на фундаментальные положения указанных наук. Любые формы конструкций из различных материалов неизбежно подвергаются силовому воздействию [10].

По результатам лабораторных исследований установлено, что с увеличением диаметра яруса

Таблица 3

Деформация пятиступенчатого образца с 24 точками двойного схождения

Показание индикатора	Деформация пятиступенчатого образца от нагрузки, мм
	0-я нагрузка	1 кг (один груз)	2 кг (два груза)	3 кг (три груза)
Начальное	0,65	0,95	0,24	0,53
Текущее		0,30	0,29	0,29
Суммарное		0,30	0,59	0,88

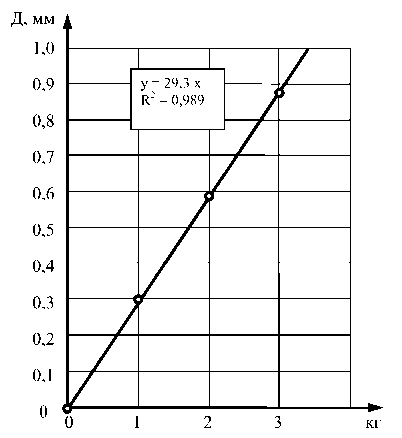
Рис. 5. Деформация пятиступенчатого образца от нагрузки с 24 точками двойного схождения

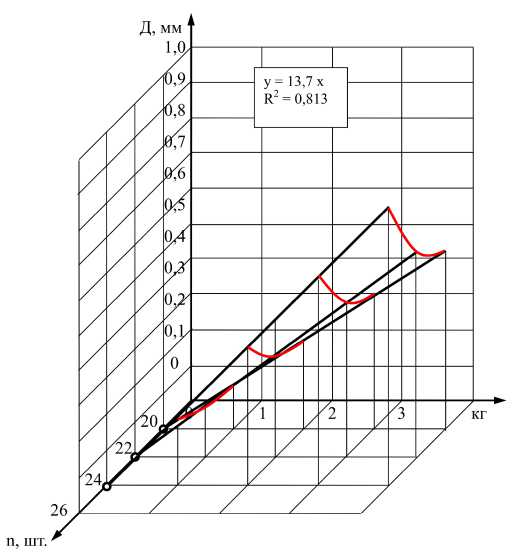
Рис. 6. Общие деформации и изменения нагрузки на узловые крепления пятиступенчатых образцов от нагрузки с 20, 22 и 24 точками двойного схождения

при постоянной высоте гиперболоидов снижается их продольная жесткость. Поперечная сила передается при малых ее значениях непосредственно на болты.

При конструировании следует стремиться к снижению аэродинамического сопротивления сооружения по отношению к господствующим ветрам.

Для высоких сооружений основную опасность несёт ветровая нагрузка, а у решётчатой конструкции она невелика. Эти особенности делают гиперболоидные конструкции прочными, несмотря на невысокую материалоёмкость [11].

Такая конструкция является жёсткой: если балки соединить шарнирно, гиперболоидная кон- струкция всё равно будет сохранять свою форму под действием внешних сил.

Усилия в гиперболоиде могут определяться как в пространственной статически определимой, так и статически неопределимых системах.

Действующими нагрузками в таких гиперболоидах являются собственный вес конструкций, масса технологического оборудования, ветровая нагрузка, обледенение, температурные перепады.

В заключение необходимо отметить, что для повышения продольной жёсткости несущих опор башни необходимо уменьшать диаметр яруса гиперболоида вращения.