Моделирование подъема воды в гидравлически попарно связанных цилиндрических капиллярах разного радиуса
Автор: И. А. Кипнис, Ю. М. Вернигоров
Журнал: Advanced Engineering Research (Rostov-on-Don) @vestnik-donstu
Рубрика: Процессы и машины агроинженерных систем
Статья в выпуске: 1 (92) т. 18, 2018 года.
Бесплатный доступ
Вертикальный восходящий поток воды в ксилеме растений обеспечивается действием сил поверхностного натяжения воды в менисках капилляров. В ряде работ показано, что распределение воды в наклонных капиллярных системах подчиняется общему правилу: в ветвях нижнего уровня продвижение воды максимально. При этом высота подъема воды в вертикальном капилляре пропорциональна количеству боковых ветвей в капиллярной системе. Ряд вопросов остаются открытыми. В их числе: роль окаймленных пор, обеспечивающих гидравлическую связь между сосудами; влияние размеров пор и параметров гидравлически связанных сосудов на подъем в них воды.
Растение, капилляры, ксилема, модель, транспирация
Короткий адрес: https://sciup.org/142211879
IDR: 142211879 | УДК: 581.1 | DOI: 10.23947/1992-5980-2018-18-1-124-131
Текст научной статьи Моделирование подъема воды в гидравлически попарно связанных цилиндрических капиллярах разного радиуса
Введение. Изучение анатомического строения и физиологии хвойных и лиственных растений [1–4] показало, что вертикальный транспорт воды обеспечивают системы вертикальных трахеид и сосудов, связанных
между собой порами. Диаметр трахеид хвойных деревьев — (20 ^ 40)•10-6 м, высота — (2,5 ^ 5)•10-3м [5]. Минимальный диаметр сосудов лиственных деревьев — 40•10-6 [5], максимальный может превышать 700 4 0 - 6 м. Длина — до нескольких метров [5] (у лиан — до 10 м [6]).
Общий объем сосудов в зависимости от породы дерева — 10-55 % объема ствола [5]. Основная функция сосудов — подъем воды в растении. Стенки сосудов покрыты не имеющими торуса окаймленными порами, с помощью которых осуществляется гидравлическая связь между сосудами (см., например, [3]). Таким образом, фактически подъем воды в сосудистой системе ствола происходит в гидравлически связанных вертикальных капиллярах различных диаметров. Ряд работ, например [7], посвящены изучению водного транспорта в растениях, в том числе методами компьютерной томографии и микроскопии [8]. Однако выше показано, что диапазон диаметров сосудов весьма широк. Поэтому эксперименты не позволяют выяснить влияние параметров гидравлически связанных окаймленными порами сосудов растений на подъем в них воды.
В [9] показано, что основным механизмом подъема воды в ветвящихся капиллярных системах является действие сил поверхностного натяжения в менисках капилляров.
В [10] изучено продвижение воды в ксилеме растений с трахеидальной проводимостью и определена величина гидравлического сопротивления одиночной окаймленной поры и их совокупности.
В источниках отсутствуют сведения о закономерностях продвижения и распределения воды в гидравлически связанных вертикальных капиллярах (сосудах ксилемы стволов).
Целью представленной работы является выявление основных закономерностей подъема и распределения воды в ксилеме растений путем моделирования продвижения воды в вертикальных гидравлически связан- ных капиллярах.
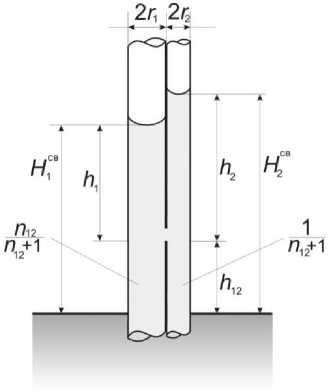
Материалы и методы. Рассмотрим систему, состоящую из двух вертикальных капилляров разного радиуса. Они соприкасаются боковыми стенками и погружены в воду. Пусть на высоте Л12 от поверхности воды имеется сквозное отверстие, соединяющее внутреннее пространство капилляров, как показано на рис. 1, а .
-
а ) b )
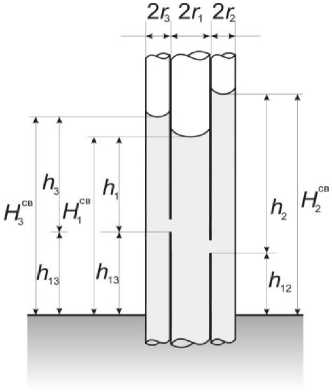
Рис. 1. Модели капиллярных систем с капиллярами, связанными одним ( а ) и двумя ( b ) отверстиями
Fig. 1. Models of capillary systems with capillaries connected by one (a) and two (b) apertures
Радиус левого капилляра равен r 1 , правого — r 2, при этом верно соотношение:
Г 1 = П 12 r 2 , (1)
где n12 = r 1 / r 2 — соотношение радиусов капилляров, п12 > 1.
Подъем воды в этой системе происходит за счет совместного действия сил поверхностного натяжения воды F Н 1 и F Н 2 в менисках капилляров.
Эта сила в общем виде описывается соотношением
F Н = 2π r σ cos α . (2)
Она прямо пропорциональна коэффициенту поверхностного натяжения воды σ, косинусу угла смачивания α и радиусу капилляра r [11]. Из рисунка можно видеть, что сила, например F Н 1 , поднимает воду в капилляре радиуса т \ в объеме этого капилляра высотой h 1 , а также часть объема воды высотой Л12 в обоих капиллярах. Это происходит благодаря наличию отверстия, связывающего капилляры, и принципу независимости действия сил. Аналогично F Н 2 независимо от F Н 1 поднимает воду в объеме правого капилляра высотой h 2 и часть
Процессы и машины агроинженерных систем
объема воды высотой h12 в обоих капиллярах. Для составления уравнения равновесия воды в системе определим, какую долю вносят F Н и F Н 2 в подъем воды в суммарном вертикальном объеме высотой h12.
Равнодействующая сил, обеспечивающая подъем воды в этом объеме, пропорциональна сумме радиу- сов капилляров, которая равна
7 1 + Г 2 = П 12 Г 2 + 7 2 = (77 12 + 1) 7- 2 .
Можно считать, что правый капилляр поднимает 1/(п12 + 1) часть воды в вертикальной общей части воды, а левый — п12/(п12+1) часть воды.
Общий объем вертикальной части системы высотой h 12 будет равен
ПГ^ + Л?2 h ;2 nT7 22 7- 2 2 h 12 + П 7- 2 2 h 12 = (77 22 + 1) n7- 2 2 h 12 .
Учитывая вышеприведенные соотношения, уравнения подъема воды в правом и левом капиллярах могут быть записаны в виде:
("22 +1)nr22h12 ,27 п
12^;2^ — РУ + ис у /уРу = 2п7 2 о cos а,
П 12
(" 122 +1) ПГ 2 2 ^ 12
(" 12 + 1)
РУ + п7-1 2 h1pу = 2nr 1 o cos а .
Отсюда:
лг2 2 ^2ру = 2nr2ocos а -
(" 22 +1) ПТ2 ^ 12
(" 12 + 1)
РУ,
nri^pg = 2nr1ocos а - п12
Решая (7) и (8) относительно h 1 и h2, получим:
(" 12 +1) ПТ 2 ^ 12
(" 12 +1)
РУ.
h =
h2
2ст cos а (" 12 +1)^:
^^^^^^^^^^^^^^^^^^^^^^^^^^ ^^^^н ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
—
" 2 РЯ
(" 12 +1)
r2 = H 0
—
( " 12 +1) (" 12 +1)
2acos а (" 12 +1)^:
^^^^^^^^^^^^^^^^^^^^ ^^^н ^^^^^^^^^^^^^^^^^^^^^^^™
—
" 1 РД (" 12 + 1)
r = H 0 —
( " 12 +1) " 2 2 , _ 0
7 12 ■ ■ ^ h 12 = H 1
12 ,
(" 12 +1)
—
" 12 (" 12 + 1)
h12 ,
где H 0 и H 0 — высоты подъема воды в одиночных вертикальных капиллярах.
Из (9) и (10) следует, что при h12 = 0 h2=H 0 , а h 1 =H 1 , то есть вода поднимается на ту или иную высоту как в одиночных, не связанных между собой отверстием капиллярах.
Высоты подъема воды Н2В и H™ в связанных отверстием капиллярах будут определяться соотношени-
ями:
H™ = h 2 + h 12 = H 2 0 — ("^ h 12 + h 12 = H 2 0 + (1 — (" 2 +) ) h 12 , (11)
( " 12 + 1) ( " 12 + 1)
H CB = h + h12 = H0 — _"л±1_ h12 + h12 = H0 + (1— -(Ф+)-) h12. (12)
1 1 12 1 " 12 (" 12 + 1) 12 12 1 " 12 (" 12 + 1) 12
Из (11) и (12) следует, что H™ = H™ =H 0 = H 0 при тг12 = 1 или h12 = 0.
Из (9) и (10) следует, что при увеличении h12 величины h1 и h2 становятся равными нулю при условии
H0 _ ( " 22 +1)
1 " 12 (" 12 + 1)
h12, H 0 = ("^ ^2.
12 2 (" 12 +1) 12
Выражая из (13) h12, получим соотношение
" 12 ( " 12 + 1) rj0
Hi
(" 22 +1) 1
( " 12 + 1) tj0
(" 12 +1) H2 ,
откуда
H 2 0 / H 1 0 = 77 12 . (15)
Полученный в (15) результат означает следующее. При заданных величинах о, а и р для двух одиночных вертикальных капилляров разного радиуса соотношение высот подъема менисков пропорционально отно-
шению радиусов капилляров.
В связанных отверстием капиллярах происходит перераспределение сил, соотношение высот подъема H™ и H™ иное, чем (15). Для определения его запишем разность (11) и (12):
HCB - HCB = H20-("^ h12 + h12 - H0 + ("22 ^ h12 - h12 = (1 - ^) ( H20 - ("^ h12).(16)
( " 12 + 1) " 12 ( " 12 + 1) " 12 ( " 12 + 1)
Из (16) следует, что H 2 B - H™ = 0 при T712 = 1.
Высота подъема воды в капиллярах одинакова также при условии hi2 = гг+) H0.(17)
12 ("22 +1)
Полученный результат интерпретируется следующим образом. При n 12 = 1 (то есть при равенстве радиусов связанных отверстием капилляров) разность высот H™ и H™ (в силу полной симметрии распределения сил в системе) будет равна нулю при любом значении h12, в том числе при h12, стремящемся к H 0 . В этом случае
Fhi = Fh2 — и система может рассматриваться как два капилляра равного радиуса (они вертикальные, независимые и погружены в воду). При п12 > 1 FН / FН2 нарушается симметрия их действия на поднимаемый объем воды. В результате согласно (17) высота h12, при которой разность высот Н2В и Н™ становится равной нулю, по мере увеличения п12 уменьшается, так как r 1 ^ r2. То же самое происходит при увеличении h12 при п12 = const. Это объясняется тем, что FН и FН2 в капиллярах одновременно, но не одинаково воздействуют на суммарный объем воды ниже отверстия в обоих капиллярах. Поэтому и связанные отверстием капилляры при Н2в - Н™ = 0 можно рассматривать как один капилляр высотой h12 с эквивалентным радиусом, равным гэ = r27^22 + 1. (18)
Пусть имеется система из трех капилляров, как показано на рис. 1, б . Центральный капилляр радиуса 7 1
связан с правым капилляром радиуса 72 и с левым капилляром радиуса 73 отверстиями, расположенными соответственно на высотах h12 и h13 от поверхности воды. Примем также, что радиус среднего капилляра соотно- сится с радиусами правого и левого капилляров, как
7 1 = п12 7 2 и 7 1 = п13 73 при п12 и п13 > 1. (19)
В этой модели возможны три варианта взаимного расположения отверстий: h12 = h13, h12 < h13, h12 > h13. Рассмотрим каждый из них.
При h12 = h13 все три силы поверхностного натяжения F Н1, F Н2 и F Н3 в менисках капилляров одновременно воздействуют на три объема воды, находящиеся ниже отверстий. При этом равнодействующая сил, обеспечивающая подъем воды в этом объеме, пропорциональна сумме радиусов капилляров, которая с учетом (19) равна:
7 + ^ 2 + ^ 3 = П 12 7 2 + 7 2 + П 12 7- 2 / П 13 = (П 1 2+1+ П 1 2 /П 13 ) 72. (20)
Тогда можно считать, что правый капилляр радиусом r 2 поднимает 1/(п12 + 1 + п12 / п13) часть. Капилляр радиусом г3 поднимает п12/ (п13(п12 + 1 + п12 / п13)). Капилляр радиусом 7 1 поднимает п12/(п12 + 1 + п12 / п13) часть объема воды общей части системы.
Общий объем вертикальной части воды высотой h12= h13 будет равен:
47- 12 ^ 12 + 47 22^2 + n73 2 h12 = (п 2 2 + 1 + п 2 2/п 2 3) лг2 2 h12. (21)
С учетом (21) уравнения подъема воды в центральном, правом и левом капиллярах могут быть записа-
|
ны в виде: |
|
|
■ ' . \ ' П ' р - + n^h . ps -2ПГ . Р cos а, п 12 + 1 + П12 /П13 |
(22) |
|
(п22 + 1 + П22/П23) nr2 h12 2 7 п П 12 + 1+П 12 /П 13 ^ + ^^ = “, |
(23) |
|
П 11 (п 11 + 1 + тг^з) пг22 ^. р5 + 2 ft = 2^7.0 cos а. П 1 3(П 1 2 + 1+ Иц /П 1з ) 33 3 |
(24) |
|
Решая, как и выше, (22)-(24) относительно h 1 , h2, h3 и далее относительно Н™,Н™,Н™ получим: |
|
|
h = Н 0 - ^ 1 + П 1 2 /П 1в ) h,2, |
(25) |
|
1 П 11 (П 11 + 1+ П 12 /П 13) |
|
|
h = Н 0 - ' h2, |
(26) |
|
2 П 11 + 1+ П 12 /П 13 |
|
|
0 _ п 32 (п 2 1 + 1 + п 2 1 /п 2 3 ) 3 3 п 1з (П 11 + 1+ Иц /П 1з ) 12 , |
(27) |
|
Н“ = Н 0 + (1 - J^ z lllZ^^) h12, |
(28) |
|
1 1 П 11 (П 11 + 1+ П 12 /пи/ |
|
|
Н2 св = Н2 0 + (1 - п 11 + 1 + п 21 /п 23 )^ 2, 2 2 V П 11 + 1+ П 12 /П 137 12 |
(29) |
|
св _ ^0 । (1 _ п 12 (п 1 2 + 1 + п 11 /п 1з ) ) 3 3 П33(П 12 + 1+ Иц /П 1з )2 12 . |
(30) |
Анализ (25)-(30) показывает, что с учетом (19)
п12 Н 0 =Н2, п 13 Н 0 = Н 0 . (31)
При п12 = п13 = 1 h1 = h2 = h3, а высоты Н™, Н2В, Н™ максимальны и соответствуют высотам подъема воды в одиночном вертикальном капилляре. Аналогичный результат получается при п12 / п13^ 1, но при h12 ^ 0. Физически это означает, что в данном случае вода в капиллярах поднимается как в трех независимых, отдельно стоящих вертикальных капиллярах разного радиуса.
Если по высоте капилляров имеется q отверстий и расстояния между ними одинаковые (h12 = h13), то высота столба воды в общей части системы увеличиваются в q раз, а h 1 , h2, h3 и Н™, Н 2 в , Н™ уменьшаются.
Процессы и машины агроинженерных систем
Оценим, при какой величине Л12 (при прочих равных условиях) Л1, Л2, Л3 и Н0в, Н™, Н3в могут стать равными нулю. Так, из (25)-(27) с учетом (31) можно получить следующие соотношения для Л12:
” 12 ( ” 12 + 1 + ” 12 /” 12) „0 _ Ь
(” 12 + 1 + ” 12 /” 1з ) Н1 " h12 , (32)
” 12 + 1 + ” 12 /п13
” 12 + 1 + ” 12 / ” 12
и12 Н0 Л12 ,
”2 2 (” 12 + 1+ ” 12 /” 12 )
” 12 (” 12 + 1 + ” 12 /” 1з )
И13 Н 0 ^ 12 .
Видно, что (32) и (33) равны и их отношение равно единице. Но отношение (32) и (33) к (34) дают в результате п43/п42 = Л12. Если при этом предположить, что Л1 = Л2 = Л3 = 0, то это возможно лишь при n43/n42 = 1, что, в свою очередь, возможно лишь при n 12 = n 13. Физически полученный результат интерпретируется следующим образом: условие Л1 = Л2 = Л3 = 0 выполняется лишь при равенстве радиусов капилляров. В противном случае указанное равенство не выполняется, уровни воды в капиллярах всегда не одинаковы и зависят от соотношения их радиусов. Это останется справедливым и в случае, если в системе будет N попарно связанных ка- пилляров.
Из (28)-(30) следует, что Н™, Н™, Н™ равны нулю при условии:
Н О = (
(” 22 + 1 + ” 12 /” 1з )
'” 12 (” 12 +1+ ” 12 /” 12)
- 1) Ли; П 12 Н О = (
- ” 22 + 1 + ” 12 /” 1з
” 12 + 1+ ” 12 /” 12
— 1) Л12 ;
„ тт 0_/” 12 (” 12 + 1 + ” 12 / ” 12 ) n h
и Н = (—тт---------:—г — 1) Л .
V”33(” 12 + 1+ ” 12 /” 12 )
Эти равенства выполняются только в случае п12 = п13 = 1.
По причинам, указанным выше, Н С в , Н2В, Н™ одновременно не могут быть равными нулю. Разность высот подъема воды в капиллярах при п12 / п13 ^ 1 может быть относительной, например, Н 0 определяется из соотношений:
Н 2 в - Н 1 св = (1
—
—) Н 0 — (1— -L) ^^-И^к h ” 12 2 ” 12 ” 12 + 1+ ” 12 /” 12
Н3 св - Н 1 св = (1
—
—) п12Н0 — (& — —) ' ^2,
” 12 2 ” 32 ” 12 ” 12 + 1+ ” 12 /” 12
/7св _ ^св = Л_ ” 12 ) эдО _ Л_ ” 12 ) ” 12 + 1 + ” 12 / ” 12
-
2 3 ” 12 2 ”и ” 12 + 1+ ”ц /” 12 12 "
Из (36)-(38) видно, что разности высот подъема воды в капиллярах равны нулю только при п12 = п13 = 1, то есть при равном радиусе всех капилляров, и принимают разные значения при п12 ^ п13 ^ 1.
При Л 12 < Л13 силы поверхностного натяжения F Н1, F Н2 и F Н3 в менисках капилляров воздействуют на три объема воды, находящиеся ниже отверстий. Суммарный их объем с учетом (19) равен:
ЛГ12Л13 + ЛГ22Л12 + ЛГ32Л13 = ((и22 + и^/пЬ) Л13 + Л12) лг2.(
Учитывая, что равнодействующая сил, обеспечивающая подъем воды в этом объеме, пропорциональна сумме радиусов капилляров с учетом (23), уравнения подъема воды в центральном, правом и левом капиллярах могут быть записаны в виде:
”12 ((”12„+ '. . +' ' Р5 + "^ =2^ cos а,(40)
” 12 + 1+ ” 12 /” 12
((”22i”2Z”i2l^i2±^i22^lip5 + пг2Лгрд = 2лг2о cos а,(41)
”12 + 1+ ”12 /”12 2 2 2'
”12«”Ъ+^2/”^^ + пг2Л3ра = 2пг3а cos а.(42)
”12(”12 + 1+ ”12 /”12 ) 3'
Если Л13 = 5 Л12 5 > 1, то решения полученных уравнений относительно Л1, Л2, Л3 и Нв, Н2В, Н3В можно записать в виде:
|
0 _ (( ” 22 + ” 12 / ” 12 ) 5 + 1) 1 1 ” 12 (” 12 + 1+ ” 12 /” 12) 12 |
(43) |
|
= ^0 _ (( ” 12 + ” 12 /” 12 ) 5 + 1) 2 2 ” 12 + 1+ ” 12 /” 12 12 , |
(44) |
|
0 _ ” 12 (( ” 12 + ” 12 /”2 2 ) 5 + 1) 3 3 ” 12 (” 12 + 1+ ” 12 /” 12 ) 12 , |
(45) |
|
Н с св = Н 0 + (5 - (( ” 12 + ” 12 /” 12 ) 5 + 1) ) Л ” 12 (” 12 + 1+ ” 12 /” 12) |
(46) |
|
Н с в = н 0 + (1 - (( ” 2 2 + ” 2 2 / ” 2 2 ) 5 + 1) ) л 2 2 v ” 12 +1+ ” 12 /” 12 ' 12 |
(47) |
|
св //0+ ” 121 (” i2 +_” i2 Z” iз 25_+ 1) ) 3 3 ” 12 (” 12 + 1+ ” 12 /” 12 ) 12 . |
(48) |
Разность высот подъема воды в капиллярах может быть определена относительно, например, Н^ из вы ражений:
Н с в — Н св =( 1 -
~) Н О -((6 -1) -(1-
) " 12
((" 12 + " 12 /" 13 ) 8 + 1) " 12 + 1 + П 12 /" 13
) Л12 ,
Н3 св - Н с в =(1 -
1^„ 7Г0 /" 32 1 ^ (( " 12 + " 12 / " 13 ) 8 + 1 м.
--) П п7 -(^— —)---------------) Л " 13 " 33 " 12 " 12 + 1+ " 12 /" 13
Н2 св
-Н 3 в = (1- " 13 ) Н 2 - ((6 -1) - (1- " 2 ) " 12 " 13
((" 12 + " 12 /" 13 ) 8 +1) " 12 + 1+ " 12 /" 13
) Л12
Из полученных соотношений видно, что при 6 = 1 выражения (43)-(48) совпадают с (25)-(30), а (46)-
(48) — с (33)-(35). При 6 = 1 и п12 = п13 = 1 вторые слагаемые в (43)-(48) равны нулю, выражения (49)-(51)
также равны нулю — и подъем воды происходит как в отдельных вертикальных капиллярах.
При Л12 ^ 0 выражения (43)-(51) описывают подъем воды в одиночных вертикальных капиллярах, в которых высота подъема воды зависит от радиуса капилляра.
Из (46)-(48) следует, что с увеличением Л13 (6 > 1) Л 1 , Л2, Л3 и Н™, Н™, Н™ уменьшаются. Физическое объяснение этого — увеличение общего объема воды в капиллярах ниже отверстий. Изменение высот Н С в , Н С в , Н С в друг относительно друга зависит от соотношения параметров системы. Так, из (49)-(51) следует, что при 6 = 1 выражения (49)-(51) совпадают с (36)-(38) и равны нулю при п12 = п13= 1 — как в независимых вертикальных капиллярах.
При п12 = 1 (радиусы правого и центрального капилляров равны) п13>1 и при прочих равных условиях:
НСв - НСв = (1 - 6) Л12,(52)
Нзсв - НСв = (1- ^) НО - (^-1)((1 ^Д)8 +1) Л12,(53)
" 13 " 13 2+ 1 /" 13
НСв - Нзсв = (1 - И13) Н2 - ((6 - 1) - (1 - -1-)((1 + 1/"2в) 8 +1) )Л12.(54)
" 13 2+ 1 /" 13
Из (52) видно, что разность Н С в - Н С в не зависит от радиуса левого капилляра. Она равна нулю при 6 = 1 или Л12 = 0 либо отрицательна, т. е. Н С в < Н С в , и ее абсолютная величина растет с увеличением 6 и Л12. Это объясняется тем, что по мере роста 6 и Л12 общий объем воды в капиллярах до отверстий увеличивается, и F Н2 поднимает больший объем воды в общей части, чем F Н1, для которой объем поднимаемой воды в левом капилляре уменьшается п13>1.
Разности подъемов высот (53) и (54) при Л12 = 0 не равны нулю, а принимают вид Н С в -Н 1 св = (1 -1/И 13 ) Н 2 (> 0), Н™ - Н С в = (1- И 13 ) Н 2 - (6 - 1) (<0).
Физический смысл этого результата заключается в том, что при уменьшении радиуса левого капилляра высота подъема воды в нем растет обратно пропорционально радиусу и превосходит Н™ и Н™.
При Л12 Ф 0 и 6 = 1 (53) и (54) совпадают с (37) и (38). При увеличении п13 (уменьшении радиуса левого капилляра) (Н 3 в - Н™) стремится к ^(Н 0 + (6 + 2) Л12/2) > 0, а (Н™ - Н 3 в ) стремится к^((1-п13) Н 0 -(6 + 1) Л12/2) < 0.
Физически это значит, что F Н3 уменьшается, высота подъема воды в левом капилляре (пропорциональна 1/г3) растет, а объем воды в общей части этого капилляра уменьшается пропорционально г3 2 . Уменьшение этого объема приводит к перераспределению сил F Н1, F Н2 в уменьшившемся общем объеме системы. В результате Н Св и Н Св увеличиваются, но остаются меньшими Н С в . Увеличение 6 при прочих равных условиях приводит к увеличению разности подъема высот, что связано с увеличением объема воды в общей части системы. При одновременном выполнении условия п12 Ф п13 > 1 и 6 > 1 Н™, Н™, Н С в описываются соотношениями (49)-(51). В случае Л12> Л13 описанный выше процесс сохраняется.
Результаты исследования. Вышеприведенные рассуждения остаются справедливыми и если в системе N попарно связанных капилляров, и при наличии нескольких отверстий по высоте. При этом в последнем случае за Л12 и Л13 принимается высота от поверхности воды до верхнего отверстия.
Общим для рассмотренных моделей является следующее. Из (25)-(30) и (43)-(48) следует, что величины Л 1 , Л2, Л3 и Н С в , Н С в , Н 3 в стремятся соответственно к Н 0 , Н 0 , Н 0 при Л12, стремящемся к нулю, и 6, стремящемся к 1. То есть чем ближе к поверхности воды расположено ближайшее отверстие в системе и чем меньше разность высот между отверстиями, тем выше поднимается вода в капиллярах.
Реальные сосуды не являются принятыми в модели классическими цилиндрами, а могут иметь форму от овала до неправильного многоугольника. Поэтому контакт сосудов осуществляется площадями смежных поверхностей, а не по образующей цилиндра. При таком строении появляется возможность реализовать рас-
Процессы и машины агроинженерных систем
пределение пор по поверхности сосуда, обеспечивающее почти непрерывное изменение их расстояния от начала до конца сосуда по высоте.

а ) b )
Рис. 2. Распределение пор на поверхности стенок сосудов в виде горизонтальных ( а ) и диагональных ( b ) рядов
Fig. 2. Distribution of pores on the surface of vessel walls in the form of horizontal (a) and diagonal (b) series
Сказанное выше подтверждается распределением пор на поверхности стенок реальных сосудов. Наиболее часто они образуют диагональные ряды (очередная поровость) или короткие горизонтальные ряды [3, 5].
Из рис. 2 видно, что расположение окаймленных пор на площади стенок сосудов обеспечивает почти непрерывное распределение пор по высоте сосуда ксилемы. Это соответствует полученным в рассматриваемой модели результатам.
Обсуждение и заключения. Построенная модель позволяет изучить физические процессы продвижения воды в сосудах ксилемы растений с учетом их анатомического строения. Высота подъема воды в каждом из гидравлически попарно связанных капилляров не одинакова (за исключением случая равенства их радиусов). В растениях это позволяет осуществлять поступление воды в параллельные сосуды, расположенные на разных высотах. Таким образом обеспечивается возможность продвижения воды в растении при газовой эмболии [7] или закупорке пор тилами в отдельных сосудах или их частях.
При равенстве высот отверстий от поверхности воды максимальный ее подъем в капиллярах происходит в двух случаях:
-
— если их радиусы равны;
-
— если отверстия, соединяющие капилляры, расположены близко к поверхности воды.
Если высоты отверстий от поверхности воды не равны (количество капилляров больше двух), то максимальная высота подъема воды в капиллярах в рассмотренных моделях обеспечивается при выполнении условий: — минимальная высота ближайшего отверстия к поверхности воды, — минимальная разность высот между отверстиями.
Чем ближе к поверхности воды расположено ближайшее отверстие в системе и чем меньше разность высот между отверстиями, тем выше поднимается вода в капиллярах. Это подтверждается характером размещения пор на поверхности стенок реальных сосудов ксилемы, образующим почти непрерывное распределение пор по высоте.
Библиографический список


