Моделирование подъема воды в системах цилиндрических капилляров разного радиуса

2 Don State Technical University, Rostov-on-Don, Russian Federation

Введение. Движение и распределение воды в растениях изучается в течении многих десятилетий и описано в монографиях по физиологии растений [1–2]. Детально описано и анатомическое строение водопроводящих путей (ксилемы) в растениях [3–5]. Многочисленные экспериментальные исследования различных аспектов движения воды в ксилеме растений опубликованы в научной литературе. Так, например, в [6] рассмотрены вопросы накопления и депонирования воды во флоэме и последующий ее возврат в ксилему при дефиците почвенной влаги. В [7] рассмотрены вопросы продвижения воды в ксилеме в условиях климатического стресса. Однако, до настоящего времени в лите-

ратурных источниках дискутируется вопрос о силах, обеспечивающих подъем и распределение воды при её продвижении в ксилеме [8].

В работах [9–11] изучено продвижение воды в ветвящихся симметричных и несимметричных капиллярных системах, все ветви которых представляют собой цилиндрические капилляры одинакового радиуса, соединенные с вертикальным капилляром того же радиуса и расположенные под углом к нему. Установлено, что наибольшее продвижение воды как в прямолинейных, так и в криволинейных боковых ветвях происходит в самом нижнем уровне и уменьшается в ветвях каждого из последующих уровней. Наличие боковых капилляров приводит к увеличению высоты подъема воды в вертикальном капилляре по сравнению с одиночным вертикальным капилляром того же радиуса. Формой растения и их части обязаны наличию в них капиллярных систем [9–11]. Доказано, что единственной силой, обеспечивающей подъем воды в ксилеме растений, является сила поверхностного натяжения воды в менисках капилляров [10]. При этом линия, последовательно соединяющая мениски воды в капиллярах ветвей разных уровней, образует фигуру, по форме напоминающую коническую крону дерева или листа. Корневое давление компенсирует, как максимум, гидравлические потери, возникающие при движении воды через систему окаймленных пор трахеид ксилемы хвойных растений [12]. Принятые в работах [9–11] модели идеализированы, но в природе такая идеализация не наблюдается. Диаметр ствола и ветвей нижних уровней больше, чем диаметр ветвей более высоких уровней и ветвей более высоких порядков. По мере роста дерева диаметр существующих ветвей увеличивается. Одновременно с этим появляются новые ветви, диаметр которых значительно меньше диаметра уже имеющихся ветвей. Диаметр капилляров центральной жилки листа больше диаметра связанных с ним капилляров листовой пластинки и т. д.

Цель работы. Определение закономерностей продвижения и распределения воды в ветвящихся капиллярных системах с капиллярами разного диаметра.

Теоретическая модель. Допустим, что имеется система, состоящая из трех капилляров разного радиуса, один из которых вертикален и погружен в воду, а остальные два наклонены под углами pj пр и pjлв к горизонтали, как показано на рис. 1, а. Примем, что радиус вертикального капилляра n > r2 + r3,r2 = nr3.                                                         (1)

Учитывая, что сила поверхностного натяжения воды Fн в мениске капилляра

Fh = 2 n r g cos a                                              (2)

прямо пропорциональна коэффициенту поверхностного натяжения воды σ, косинусу угла смачивания α и радиусу капилляра r [12], определим какую долю вносит каждый из наклонных капилляров в подъем воды в вертикальном капилляре. Равнодействующая сил, обеспечивающая подъем воды в вертикальном капилляре, пропорциональна сумме радиусов наклонных капилляров:

r ₂ + r ₃ = nr₃ + r ₃ = ( n + 1) r ₃.                                                    (3)

Можно считать, что правый капилляр поднимает 1/( n +1) часть воды в вертикальном капилляре, а левый n /( n +1) часть воды. Обозначим высоту вертикального капилляра через h . Величины продвижения и высоты подъема воды в правой и левой ветвях обозначим соответственно через L ¹ _{1 пр} , L ¹ _{1 лв} , h ₁ ¹ _пр , h ₁ ¹ _лв .

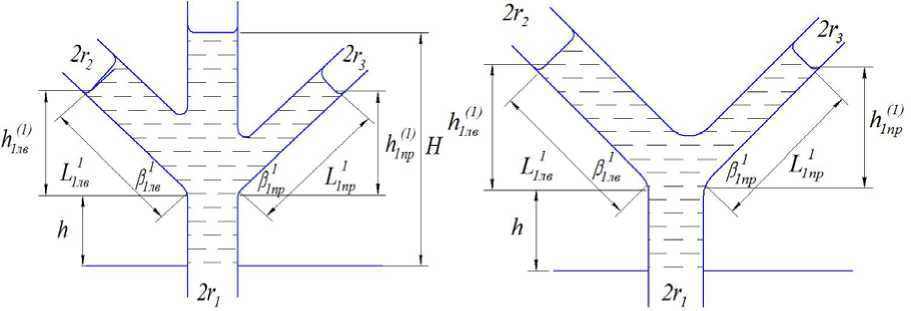
а)

б)

Рис. 1. Модели капиллярных систем с капиллярами разного диаметра

Механика

Учитывая эти соотношения и полагая в (2) α = 0, уравнения продвижения воды в капиллярах правой и левой ветвей могут быть записаны в виде:

^- Л - P gh + Л ^r 32 p gL пр sin Р 1 пр = ^{2 п} - О , n + 1

-n - п - 1 ² p gh + п n ² - 32 p д!^ лв sin p [ лв = 2 n n- , ^ . n + 1

Сокращая обе части уравнений (4) и (5) на п - ₃ ² p g получим:

11       1 r ²    1

L1 пр sin Pi пр = h3--7 (Jf)h = h11пр , n + 1 -32

L лв sin P i лв = !( h 3 n

—

-   ( - L) h ) = h ¹ лв ,

( n + 1) - 3

где h 3 — высота подъема воды в одиночном вертикальном капилляре радиуса r 3.

Из (6) и (7) следует, что высота подъема воды в левом капилляре большего радиуса в n раз меньше, чем в правом, а разность высот подъема составляет

, 1       11      1        1    /^- 12         1 7          1      /^- 12         ( n — 1)

h1 пр — h1 лв = h3--7<ут)h —  h3 + ——к(~) h =-----(h n +1 -2     n     n (n +1) -2        n

—

1    h ( ^{r 12})).

n + 1    - ₃ ²

Таким образом, разность высот подъема воды в наклонных ветвях не зависит от угла наклона ветвей, а зависит только от соотношения радиусов капилляров.

При n =1, -2= -3, h1пр — h1лв = 0, p[пр = p[лв,h1пр = h1лв = h3 — ^h, что полностью совпадает с результатами, полу- ченными в [1].

Из соотношений (6) и (7) можно также видеть, что продвижение воды в левой и правой ветви при n ≠ 1 не одинаково. В частности, из (7) следует, что продвижение воды и в левом капилляре большего радиуса при условии Р 1 _пр = Р 1 лв в ^п раз меньше, чем в правом. При в 1 _пр = p j _лв = 0 наклонные ветви располагаются горизонтально. В случае, когда p j _пр = p j _лв = 90 0 , наклонные ветви принимают вертикальное положение, а разность высот подъема воды в них определяется соотношением (7). Отношение

L 1 пр / L 1 пр = ⁿ

sin р ! пр

«« р ! лв

показывает, что продвижение в наклонных капиллярах зависит от соотношения как радиусов, так и углов наклона к горизонтали.

Полагая в (6) или (7) h 1_пр = h 1_лв = 0, можно определить критическую высоту h _кр при которой вода из вертикального капилляра не будет поступать в наклонные ни при каких условиях:

h3--(-у) h = 0, n +1 -32

1 r2

h3 =     (^)h ^ h = hкр = h3 (n + H';)

n +1 -3

В модели на рис. 1, б подъем воды происходит под действием сил поверхностного натяжения в менисках трех капилляров, имеющих разные радиусы. Как и в предыдущем случае, выполняется условие (1), а соотношение радиуса вертикального капилляра с меньшим из боковых капилляров равно r1 = mr3 . Тогда правый боковой капилляр поднимает в общей части вертикального капилляра на высоту h только         часть объема воды, левый боковой капил- m + n +1

nm ляр        , а вертикальный — остальную часть объема воды, пропорциональную.

m + n + 1                                                                 m + n + 1

В этом случае уравнения, описывающие продвижение воды в боковых капиллярах и высоту ее подъема H в вертикальном капилляре запишутся следующим образом:

----1  п-12рgh + п-32pgL1 пр sin Р1 пр = 2п 1-3,0, m + n +1

n 2     211

--------- Л ^- 1 p gh + Л - 2 p gL 1 лв si ⁿ Р ₇лв = ^{2 п} - 2 G , m + n +

m

---------п r 1 р gh + ( H - h ) п r 1 p g = 2 п r 1 G .                                      (13) m + m + 1

Сокращая (11), (12) и (13) соответственно на п r ₃ ² р g , п r ₂ ² р g и п r 1 ² р g получим выражения для Д , L 1 лв и H :

Lпр sin в1пр = h3 -    -    (-^h = h1пр,(14)

m + n + 1 r ²

Ь\лв sin P1 лв = h2n— (rL)h = h^B,(15)

m + n + 1 _r 2 ²

H = h1 + (1--n)

m + n + 1

Из (14)–(16) следует, что с увеличением m и n (что эквивалентно уменьшению r3 ) порознь или одновременно величины L11пр , L11лв, h11пр , h11лв и H уменьшаются. Высота подъема воды при этом в капилляре малого радиуса увеличи- вается, так как высота подъема воды в одиночном капилляре h3 обратно пропорциональна радиусу капилляра r3 , а коэффициент перед вторым слагаемым в (14) пропорционален первым степеням m и n. При m = n =1 уравнения (14)– (16) совпадают с аналогичными уравнениями в [9] и описывают распределение воды в аналогичной системе с капиллярами равных радиусов. Высота подъема воды в вертикальном капилляре не зависит от угла наклона ветвей, а зависит только от соотношения радиусов капилляров. При этом величина hкр определится для правой и левой ветвей соотношениями:

r ²

hkpnp = (m + n +1)( ^) h3, r12

m + n + 1 r ₂ ²

hкрлв =---------(—)h2 .

nr

Физический смысл соотношений (17) и (18) состоит в том, что изменение радиуса любого из капилляров приводит к перераспределению действующих сил и при определенном соотношении размеров капилляров действующие в системе силы не обеспечивают подъем воды выше h. Нетрудно видеть, что h _крпр = h _крлв. Учитывая [1], что h 2 =2σ cos α/ r 2 ρg и условие r 2 = nr 3 получим h 2 =2σ cos α/ nr 3 ρg, откуда h 2 = h 3 / n . Подставляя последнее соотношения в (18) получим:

m + n +1 2 Z;2x hr h = hкрлв =--------n П") 3 = (m + n + 1)(Л)h3 = hkpnp.

nr12nr

Разность высот подъема воды в боковых ветвях описывается соотношением hlnp - ht,e = h3 - h2 +   r12   (4 - 4)h(20)

m + n + 1 r ₂ ² r ₃ ²

и при m = n =1 становится равной нулю.

Анализ уравнений (17), (18) и (20) затруднителен из-за большой вариабельности соотношений величин m , n и h . Однако, построив графическое 3D изображение этих уравнений, можно получить представление о изменении разности высот подъема воды в ветвях и о изменении h _кр в широком диапазоне изменения величин m , n и h . Разделив обе части (17) на h ₃ и учитывая, что r 1 = mr 3 , получим:

h kpnp = m + n + 1 h 3        m ²

Результаты построения графиков для h _кр, с учетом (1), представлены на рис. 2.

Выбор h3 в качестве нормирующей величины обусловлен следующими соображениями. Правый капилляр имеет наименьший радиус r3 и, следовательно, высота подъема воды в одиночном вертикальном капилляре этого радиуса будет наибольшей по сравнению с капиллярами радиусов r1 и r2 [9]. Поэтому диапазон отношений hкрпр / h3 бу-

Механика

дет находиться в пределах от 0 до 1 и может быть однозначно задан при построении 3D графиков.

Анализ графиков на рис. 2 позволяет выяснить, как изменяется величина h _кр при изменении соотношения радиусов капилляров. Так, например, на рис. 2, а m =3, n изменяется от 1 до 2, а величина h _кр находится в пределах ≈ 0,55 – 0,75 h ₃. Увеличение радиуса вертикального капилляра приводит к уменьшению h _кр и при m=10 h _кр ≈ 0,17 h ₃.

Увеличение радиуса левого капилляра до n от 1 до 4 при m =5 (рис. 2, в ) и выполнении условия (1) приводит к уменьшению критической высоты, которая в этом случае находится в пределах ~ 0,24 - 0,4 h 3 . С увеличением радиуса вертикального капилляра h _кр уменьшается и при m =10, h _кр ~ 0,15h₃.

В случае, представленном на рис. 2, б, радиус r 1 больше радиуса r ₃ в 10-20 раз, а r ₂ может быть равен r₃ или превышать его до 9 раз. При этом соотношение r 1 / r ₂= mIn . Можно видеть, что при m=10 и изменении n от 1 до 9 величина h _кр находится в пределах ~ 0,17-0,2 h ₃, уменьшаясь при увеличении m до 20 до значения h _кр ~ 0,13h₃.

Общей закономерностью в рассмотренных случаях является то, что h _кр тем больше, чем меньше разница в радиусах вертикального и боковых капилляров. С увеличением разницы в радиусах h _кр уменьшается, асимптотически приближаясь к нулю. Физическая интерпретация полученных результатов состоит в следующем. С увеличением h (рис. 1, б) или r 1 одновременно происходит несколько процессов. Вес воды в его нижней части высотой h увеличивается пропорционально r ₃ ² , а F _н пропорциональна r 1 , вследствие чего уменьшается высота подъема воды [9].

h крпр h3

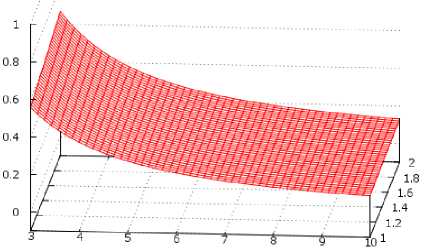
m

а)

h _ крпр h3

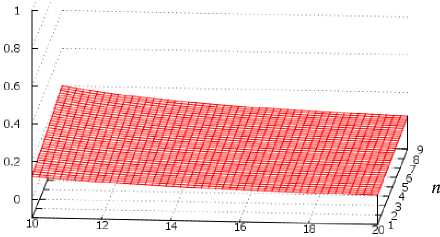
m

б)

h крпр h3

n

m

в)

Рис. 2. Зависимость h _крпр I h ₃ от соотношения m и n в диапазонах изменения: а) m от 3 до 10, n от 1 до 2; б) m от 10 до 20, n от 1 до 9; в) m от 5 до 10, n от 1 до 4

В этом случае силам поверхностного натяжения в менисках боковых капилляров приходится «поднимать» пропорциональный их радиусу больший объем воды (высотой h). При этом следует ожидать уменьшения поступления воды в боковые капилляры. И при достижении какого-то значения r1 или h вода в боковые капилляры поступать не будет (hкр).

Соотношение (20), описывающее разность высот подъема воды в боковых капиллярах, можно также представить в 3D графике. Выражая r 1 и r ₂ через r ₃, учитывая, что h ₂= h ₃/ n и нормируя по h ₃, получим следующее соотношение:

h1np - hлв = 1 -1 + -m— (1 -1)5, (22) h3 n m + n +1 n где 5 = h/h3. Выражение (22) содержит 3 переменных: m, n и 5. Поскольку (22) нормировано по h3, то (h1пр - h1лв)/h3 и δ изменяются в пределах от 0 до 1. Задавая теперь один из параметров постоянным, например, m, можно построить любую серию 3D графиков для (22). Некоторые из них представлены на рис. 3.

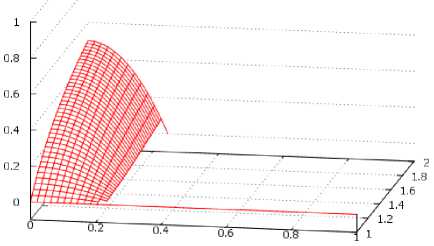
Анализ этих графиков показывает следующее. Если r 1 не сильно превышает r2 и r3 (рис. 3, а), то при 5=0 и h=0 величина (h1пр - h1лв) изменяется от 0,5h3 (при n=2) до 0 (при n=1). Физическая интерпретация этого заключается в том, что при n =1, r2 = r3 каждый из трех капилляров оказывается независимо от остальных погруженным в источник воды и ее подъем в них определяется также, как и для одиночного погруженного в воду капилляра. При δ=0 (h=0) и n=2, r2 = 2r3 объем поднимаемой воды увеличивается и h1 пр - h1лв = 0,5h3 По мере увеличения h и n (одновременно или порознь) разность h1пр - h1лв уменьшается, так как Fн в обоих боковых капиллярах частично и пропорционально радиусу расходуется на подъем воды на высоту h в вертикальном капилляре. При достижении 5~0,7 (h~0,7h3) выражение h1пр - h1лв становится равным нулю, так как величина h становится равной hкр и вода в боковые капилляры не по- ступает.

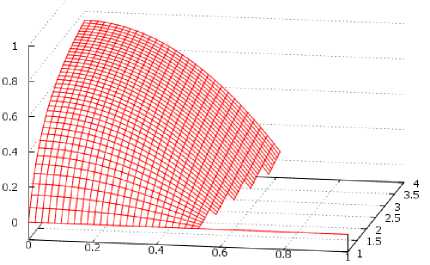
Если r 1 увеличивается до m=10 (рис. 3, б) и 1< n<2, то все приведенные выше рассуждения сохраняются. Но h кр уменьшается и становится равной ~0,2h 3, что связано с перераспределением сил в системе из-за необходимости подъема увеличившегося объема воды высотой h. Справедливость этого вывода проиллюстрирована на рис. 3, в. Если m =10, а 1< n<9, то при n=1 и 5=0 по причинам, указанным выше, разность h1 пр - h1лв = 0. По мере роста n разность высот подъема воды в правом и левом капилляре увеличивается и достигает 0,9h 3 при n=9, то есть в правом капилляре вода поднимается в 9 раз выше, чем в левом, что вполне справедливо для одиночных погруженных в воду капилляров. По мере увеличения 5 выражение h1пр - h1лв уменьшается до нуля при величине h в диапазоне 0,3h3-0,4h3, который является критическим. Сравнивая эти критические величины с таковыми на рис. 3, а и рис. 3, б можно видеть, что hкр (рис. 3, в) находится в промежутке между величинами hкр на рис. 3, а и б.

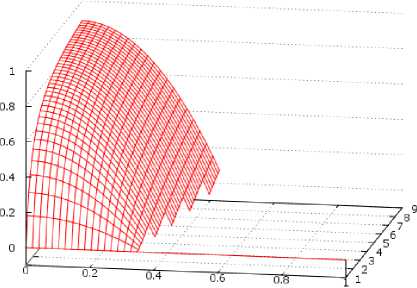
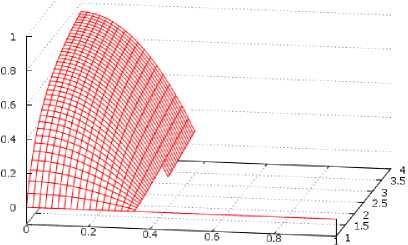
Графики для других соотношений величин m и n, продемонстрированных на рис. 3, г и рис. 3, д, проявляют ту же тенденцию изменения h1пр - h1лв, как описано выше. Различие состоит только в скорости изменения h1пр - h1лв и достижения h кр.

^{1 1} -й¹

h1 пр h1 лв h3

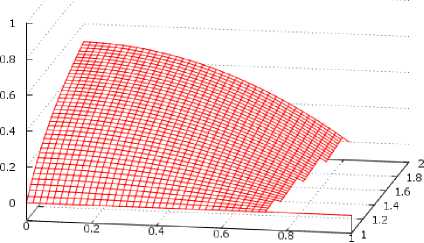
h / h 3

а) для m =3, n = 1-2

Механика

^{1 1}  -й¹

hl пр   h1 лв h3

n h / h з

hl пр   hl лв h3

б) для m =10, n = 1-2

n h / h з

^{1 1} -й¹

h1 пр h1 лв h3

в) для m =10, n =1-9

h / h з

^{1 1} -й¹

h1 пр h1 лв h3

г) для m =5, n =1-4

n h/h3

д) для m =10, n =1-4

^{1 1}  -й¹

hl пр   h1 лв h3

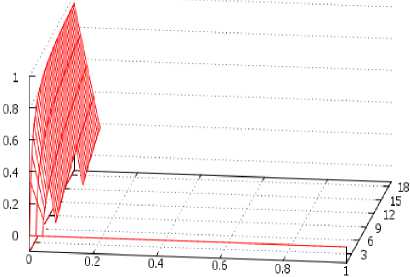
n h/h3

е) для m =20, n =1-19

Рис. 3. Зависимость

11 -й1 hl пр h1 лв h3

от соотношения параметров m , n и 8 при фиксированных значениях m .

Величины m и диапазон изменения n указаны в подрисуночных надписях

Более наглядно это можно видеть на рис. 3, е, где m =20, а 1< n <19. Видно, что при увеличении n от 1 до 19 разность высот изменяется при n =1 и 8=0 от 0 до —0,95 h ₃ и по мере увеличения 8 уменьшается до нуля при h _кр в диапазоне 0,2 h ₃-0,3 h ₃.

Применяя описанную выше методику к (16), получим соотношение для построения в 3D графике величины H / h 1 в виде

H / h = 1 + (1 - m /( m + n + 1)) 5 H ,                                       (23)

где 8_H = h / h i ; h 1 — высота подъема воды в одиночном вертикальном капилляре радиуса r 1 . Нормирование по h 1 обусловлено следующим. В [9] показано, что наличие боковых капилляров в ветвящейся системе приводит к увеличению подъема воды в связанном с ними вертикальном капилляре. Поэтому H / h 1 > 1, в то время как 0< 8_H = h / h 1 <1.

H/h 1

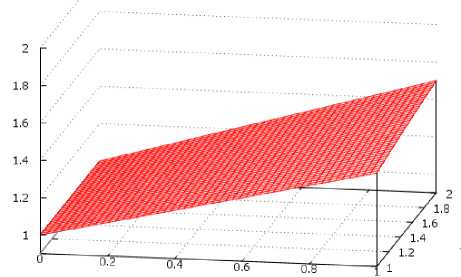
h/h 1

• а)    для m =3, n =1-2

  H/h 1

  

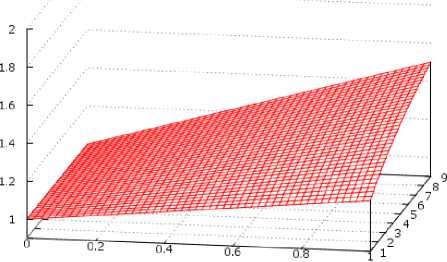
  h/h 1

  
  

  Механика

  
  

• б)    для m =10, n =1-9

  H/h 1

  

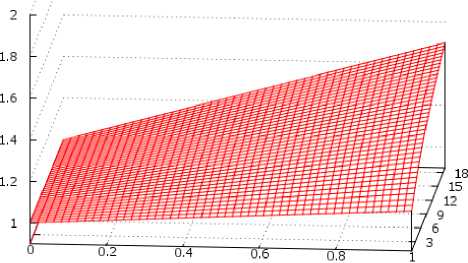
  h/h 1

  
  

• в)    для m =20, n =1–19

Рис. 4. Зависимость H / h ₁ от соотношения параметров m , n и δ_H при фиксированных значениях m . Величины m и диапазон изменения n указаны в подрисуночных надписях

Результаты построения графиков для H / h 1 , при различных значениях m , n и δ H , представлены на рис. 4. Из рис. 4 а, б, в следует, что при любом соотношении параметров m , n и δ_H=0, H = h ₁ , то есть вода поднимается как в одиночном вертикальном капилляре радиуса r 1 . Если радиусы вертикального и боковых капилляров отличаются несущественно (рис. 4, а), то высота подъема воды в вертикальном капилляре по мере увеличения δ_H увеличивается и при достижении δ H =1, в зависимости от n , H ≈1,3 h 1 –1,5 h 1 . Физически это означает, что наличие боковых капилляров позволяет воде подняться на высоту, превышающую h ₁ в 1,3 раза. При увеличении m , n , как показано на рис. 4, б при m =10, величина подъема воды зависит от величины n . Так при n =1, H ≈1,17 и при n =9 достигает значения H ≈1,5. Физический смысл этого заключается в том, что по мере роста n (при m =const), боковые капилляры берут на себя все больше «работы» по подъему воды в вертикальном капилляре, позволяя силе поверхностного натяжения в нем поднять воду на большую высоту. Если m =20 (рис. 4, в) и n =1, H ≈1,09, а при n =19, H ≈1,5. Таким образом, при n =1 величина H уменьшается, а при дальнейшем росте m , n увеличивается, асимптотически приближаясь к H =2.

Аналогичным образом можно построить 3D графики для h ₁ ¹ _пр , h ₁ ¹ _лв и, задавая величины углов β ¹ _{1 лв} , β ¹ _{1 пр} ,для

L 1 пр , L 1 лв .

Выводы.

• 1.    Построена модель подъема воды в капиллярной системе с цилиндрическими капиллярами разного радиуса. Вследствие большого количества переменных и их высокой вариабельности для анализа полученных соотношений авторы воспользовались 3D графикой.

• 2.    Показано, что изменение параметров капиллярной системы приводит к перераспределению действующих в ней сил и разность высот подъема воды в боковых капиллярах может изменяться от 0 до 0,95 высоты подъема воды одиночного вертикального капилляра системы, имеющего наименьший радиус.

  
  

• 3.    Установлено, что при определенных соотношениях параметров капиллярной системы существует критическая высота, при которой вода в боковые капилляры не поступает. С увеличением разницы в радиусах вертикального и боковых капилляров или увеличением высоты части вертикального капилляра, на которую действуют силы поверхностного натяжения, критическая высота уменьшается.

• 4.    Высота подъема воды в вертикальном капилляре зависит от соотношения радиусов вертикального и боковых капилляров, а также от высоты части вертикального капилляра, предшествующей разветвлению. Если величина последней равна нулю, то подъем воды в вертикальном капилляре не зависит от наличия боковых капилляров. Увеличение радиусов боковых капилляров при наличии общей части вертикального капилляра и при постоянстве его радиуса приводит к повышению уровня воды. Это связано с уменьшением разницы в радиусах боковых и вертикального капилляров. Боковые капилляры принимают все большее участие (пропорциональное их радиусам) в подъеме воды в общей вертикальной части. При этом высота подъема воды в вертикальном капилляре в рассматриваемой модели может до 2-х раз превышать высоту подъема воды в одиночном вертикальном капилляре того же радиуса.