Моделирование подготовки поверхности при восстановлении и упрочнении деталей сельхозтехники газопламенным напылением

М ОДЕЛИРОВАНИЕ ПОДГОТОВКИ ПОВЕРХНОСТИ ПРИ ВОССТАНОВЛЕНИИ И УПРОЧНЕНИИ ДЕТАЛЕЙ СЕЛЬХОЗТЕХНИКИ ГАЗОПЛАМ ЕННЫ М НАПЫ ЛЕНИЕМ

Проведены исследования накатывания на резьбах замкового профиля . Разработана методика моделирования процесса методом конечных элементов . Определены силы деформирования , поля напряжений и деформаций в заготовке при накатывании замкового профиля . Установлено , что наиболее рациональными являются значения степени обжатия профиля 1,1…1,5.

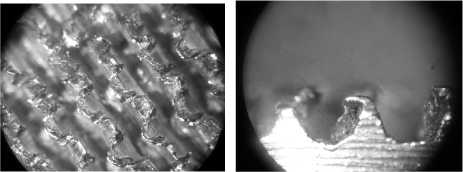
Известно [1, 2], что одним из наиболее эффективных способов подготовки поверхностей деталей машин под газопламенное напыление , обеспечивающим значительное повышение прочности сцепления покрытия с подложкой , является накатывание на восстанавливаемой или упрочняемой поверхности заготовки резьб с замковым профилем . Резьба с замковым профилем представляет собой треугольную резьбу , на вершине которой формируются полугрибовидные участки профиля , смещенные попеременно в разные стороны ( рис . 1). Этот профиль выполняет роль полуанкерного замка , на который механически прикрепляется напыленный слой . Восстанавливаемая или упрочняемая поверхность детали предварительно протачивается на токарном станке , затем на ней нарезается « рваная » резьба . Накатывание замкового профиля производится на предварительно прорезанной резьбе . В качестве инструмента используются резьбонакатные ролики ( рис . 2), выполненные в виде цельного диска , правая и левая поверхность которого по краям имеет конические выступы 1 и 2, разделенные сквозными пазами 3 и 4, при этом каждый выступ правой 1 и левой 2 поверхности диска расположен напротив пазов 3 и 4 этих поверхностей , соответственно . Сквозные пазы образуют на конических выступах выступы и впадины с постоянным шагом , при этом пазы на правой 3 и левой 4 сторонах диска расположены в шахматном порядке . Державку с резьбонакатным роликом устанавливают в резцедержатель токарного станка под прямым углом и выбирают продольную подачу ( рис . 3), равную шагу обрабатываемой резьбы . В связи с тем , что рабочая высота конических выступов меньше высоты профиля резьбы , то при внедрении вершин выступов во впадину резьбы диск деформирует вершину резьбы , деформированный металл течет внутрь от каждого конического выступа . При накатывании замкового профиля происходит наклеп витков резьбы , что ведет к повышению усталостной прочности восстанавливаемых или упрочняемых деталей .

Процесс формообразования замкового профиля на резьбах в настоящее время практически не изучен . Для определения рациональной технологии накатывания необходимо исследовать характер влияния основных технологических факторов процесса на поля напряжений и деформаций в заготовке и силы деформирования . Поскольку экспериментальные исследования локальной поверхностно - объемной пластической деформации при резьбонакатывании весьма трудоемки и дорогостоящи , приоритет должен принадлежать теоретическим методам .

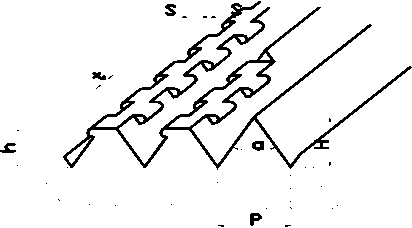
Р - шаг нарезаемой « рваной » резьбы ; Н - высота исходного профиля ; h - высота профиля после обжатия ; α - угол профиля ; t - шаг накатывания ; S - выступание гребня

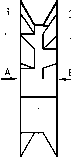
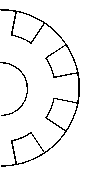
Рисунок 1 – Геометрические параметры резьбы с замковым профилем

Рисунок 2 – Накатные ролики : 1 и 2 – конические выступы ; 3 и 4 – сквозные пазы

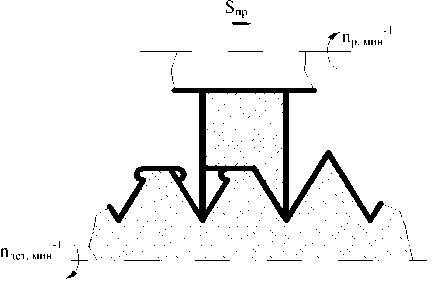
Рисунок 3 – Схема образования профиля поверхности деформированием предварительно нарезанной резьбы на токарном станке : n дет – частота вращения детали ; n р – частота вращения рабочего органа ; S пр – продольная подача

Ma т ep и a лы и мет o дик a исследований

Для определения контактных давлений при накатывании резьб в настоящее время наибольшее применение нашел метод линий скольжения . Существенным недостатком данного способа является то , что он позволяет определять только контактные давления и не имеет возможности выявить распределение напряжений и деформаций по всему объему тела . Кроме того , данный метод является приближенным . Применительно к резьбонакатыванию использование данного метода требует сведения сложного объемного напряженно - деформированного состояния к плоскому ( внедрение пуансона в полуплоскость ), что существенно снижает точность расчетов .

В связи с этим для моделирования резьбонакатывания представляется перспективным использование современных численных методов математического моделирования , в частности метода конечных элементов ( М КЭ ). В настоящее время создано множество программных продуктов для ПЭВМ , реализующих МКЭ , однако для исследования напряженно - деформированного состояния инструмента и заготовки при резьбонакатывании наиболее целесообразно использование специализированных программ инженерного анализа , предназначенных для моделирования процессов пластической деформации . К ним относятся MSC.SuperForm, MSC.SuperForge, DEFORM и др . Для моделирования процесса накатывания замкового профиля на резьбе был использован одним из мировых лидеров в области моделирования процессов обработки давлением и резанием – пакет программ DEFORM 3D, разработанный компанией Scientific Forming Technology Corporation (SFTC, СШ А ). Данный программный продукт позволяет моделировать сложные трехмерные процессы пластической деформации и разрушения материалов .

При использовании МКЭ чрезвычайно важной является корректная постановка начальных и граничных условий . При моделировании процесса сделаны следующие допущения :

• -    инструмент абсолютно жесткий ;

• -    заготовка идеально пластичная ;

• -    резьба представлена в виде двух кольцевых канавок ;

• -    качение инструмента по поверхности детали происходит без проскальзывания .

Геометрические 3D модели заготовки с прорезанными кольцевыми канавками и ролика для накатывания замкового профиля на резьбе были сформированы в системе T-Flex CAD 3D и экспортированы в DEFORM 3D.

Предварительными исследованиями установлено [3], что основными факторами, влияющими на прочность сцепления покрытия с основой, являются шаг нарезаемой резьбы Р, выступание гребня S полугрибовидного профиля и шаг накатывания замкового профиля t, характеризующий длину гребней попеременно смещенных в правую и левую стороны и зависящий от шага пазов в накатывающем ролике.

В результате деформирования вершин резьбы форма получаемой вершины полугрибовидного профиля напрямую зависит от степени обжатия профиля ẟ – безразмерной величины , характеризующей отношение высоты исходного профиля Н к высоте профиля после накатывания h ( рис . 1).

5=H, h

где Н - высота исходного профиля ;

• h    – высота профиля после накатывания .

Поскольку , при операции накатывания на резьбе замкового профиля происходит перераспределение металла с вершины в одну сторону , то можно считать , что чем выше значение ẟ , тем больше будет выступание гребня S вершины в сторону ( при δ _min=1 гребень отсутствует ).

Зависимость между S и ẟ можно проследить из подобия треугольников исходного профиля и смещаемой в сторону вершины .

н _

5 = 2 P— = 2 P 5 . h

Допустим , что металл , смещаясь с вершины в одну из сторон , образует гребень в форме равностороннего треугольника . Также можно считать , что одна из сторон треугольника исходного профиля равна шагу Р . Таким образом , высота нарезаемого профиля H определяется из выражения :

• — = P • cos a , (3) где α – угол профиля нарезаемой резьбы . При подготовке поверхности под газопламенное напыление целесообразно нарезать резьбы со стандартным углом профиля α =60⁰.

Подставив (3) в (1), получим :

5 = P-cosa = о,87 ^ P . hh

Следовательно , ẟ – интегральный показатель , характеризующий одновременное влияние четырех параметров замкового профиля : Н , h, α и S на прочность сцепления покрытия с основой .

Задача по определению рациональной технологии накатывания на резьбе замкового профиля решалась варьированием важнейшего фактора , влияющего на образование полугрибовидного замкового профиля : степени обжатия профиля δ . Диапазон варьирования значений ẟ = 1,1…1,5, обоснован целесообразностью получаемого профиля ( во избежание смыкания соседних витков ) и пределами прочности резьбы и самого инструмента . Предварительно проведенными экспериментальными исследованиями установлено , что для обеспечения высокой прочности сцепления покрытия с основой наиболее рациональными являются значения шага резьбы P =1,25 мм и шага накатывания замкового профиля t =1,25 мм [4], что и было принято при моделировании .

Диаметр накатного ролика при моделировании принимался равным 6,5 мм , а диаметр заготовки 20 мм .

Особенностью моделирования различных физических процессов с помощью современных программ, реализующих МКЭ, является необходимость сохранения заготовкой неподвижности, все движения обработки следует прикладывать к инструменту. В связи с этим, при моделировании накатному ролику сообщаются два вращательных движения с одинаковой окружной скоростью равной скорости накатывания: собственное вращательное движение вокруг своей оси и вращательное движение вокруг оси заготовки, имитирующее вращение заготовки вокруг своей оси.

Численные значения угловых скоростей определялись исходя из рекомендуемой скорости накатывания и диаметров инструмента и детали .

В результате предварительных исследований установлено, что рекомендуемая скорость накатывания замкового профиля на легированных сталях V=10 м/мин. Следовательно, частота вращения детали составит:

1000V nдет =  — , мин рdд

где d _д – диаметр восстанавливаемых поверхностей детали , мм ;

V – скорость накатывания , м / мин .

Следовательно , частота вращения инструмента n _р для накатывания ( при условии отсутствия проскальзывания ) определяется следующим образом :

n р = n д d ^ , мин - 1 d _р

где d _р – диаметр накатного ролика , мм .

Для сокращения потребного количества конечных элементов и, следовательно, времени расчета, моделирование целесообразно производить лишь для одной четверти заготовки. На месте удаленных частей заготовки прикладываются компенсирующие их граничные условия: запрет на перемещения по осям, перпендикулярным к плоскости разреза. При задании параметров разбиения заготовки на конечные элементы максимальной принималась зависимость степени измельчения сетки от величины эквивалентных деформаций.

Ш аг вычислений по времени выбирался таким образом , чтобы обеспечить перемещение инструмента относительно заготовки за один шаг расчета на расстояние , не превышающее минимальной длины стороны конечного элемента .

В качестве материала заготовки выбрана сталь 20 ХГНМ , часто применяемая для изготовления ответственных деталей автомобильной , сельскохозяйственной и строительной техники . Задание физико - механических свойств материала заготовки обеспечивалось выбором соответствующей стали из имеющихся в программном комплексе библиотек материалов . При этом использовалась мультилинейная кинематическая модель упрочнения .

Результаты исследований

При моделировании процесса накатывания на резьбах замкового профиля получены форма и размеры профиля ; значения сил , действующих на накатывающий инструмент в направлении осей координат ; а также поля эквивалентных напряжений и деформаций , возникающих в восстанавливаемой детали .

В результате моделирования установлено , что геометрия замкового профиля формируется полностью , а форма и размер профиля после накатывания подтверждает главнейшее влияние степени обжатия профиля на выступание гребня .

Силы , действующие на накатывающий инструмент , также зависят от степени обжатия профиля ( рис . 4). Значение нормальной силы при увеличении степени обжатия профиля возрастает в 1,5 раза (F _х =1659…2516 Н ). Существенного влияния степени обжатия на максимальную осевую силу не отмечено (F у =946 Н ). Величина касательной силы с увеличением степени обжатия профиля возрастает в 1,8 раза (F z =737…1336 Н ).

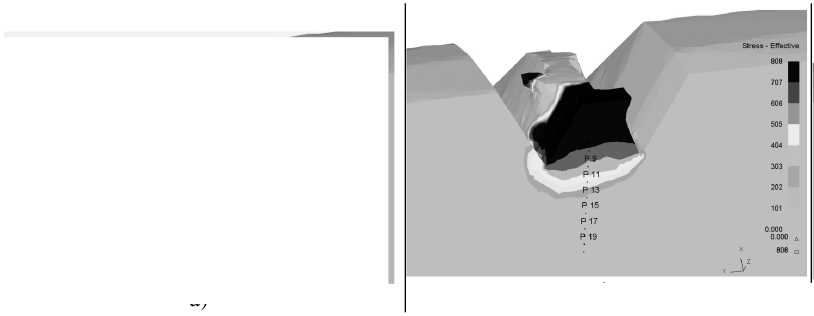
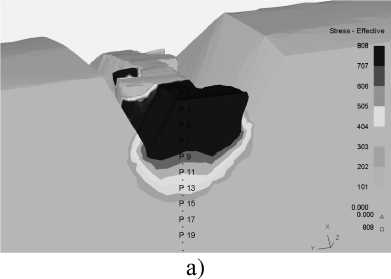
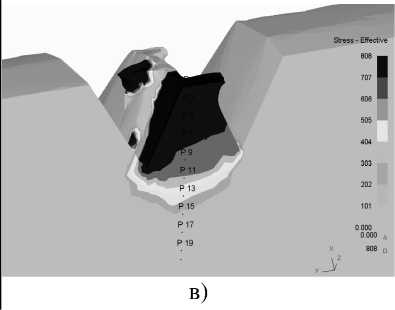
Распределение эквивалентных напряжений по М изесу в витке накатываемой резьбы приведено на рисунках 5 и 6. Характер и величина эквивалентных напряжений свидетельствует , что максимальные значения приходятся на вершину в месте образования замка и достигают у поверхности 805 МПа .

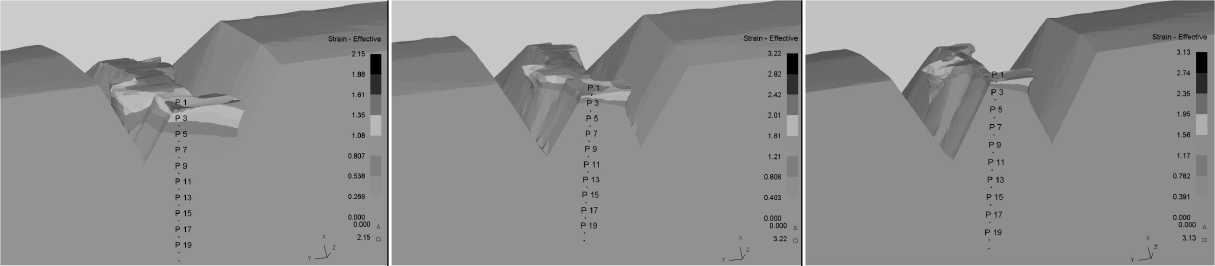
Распределение эквивалентных деформаций , по М изесу , в витке накатываемой резьбы приведено на рисунках 7 и 8. Эквивалентные деформации резьбы при накатывании позволяют судить о возможном повышении микротвердости и степени упрочнения исходного материала детали . Эквивалентные деформации распределяются в зависимости от степени обжатия профиля , достигая значения 1,55. При степени обжатия профиля 1,1 упрочняется лишь вершина резьбы , а при степени обжатия 1,5 упрочненным является весь резьбовой профиль . Упрочнение достаточно равномерно , а глубина упрочнения составит более 2,6 мм .

Варьируя степень обжатия профиля в диапазоне 1,1…1,5, можно обеспечить требуемые степень и глубину упрочнения резьбы с замковым профилем .

Выводы

Расчет сил деформирования показывает , что накатывание замкового профиля на резьбах может осуществляться на универсальных станках токарной группы . При этом величина напряжений и деформаций при накатывании не превышает предельно допустимых значений и не приведет к разрушению резьбы на заготовке . Разработанные рекомендации могут быть использованы при проектировании технологических процессов восстановления и упрочнения деталей машин газопламенным напылением покрытий .

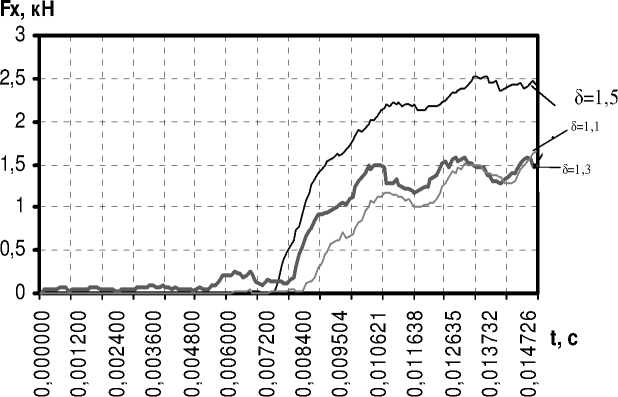
Fy, кН

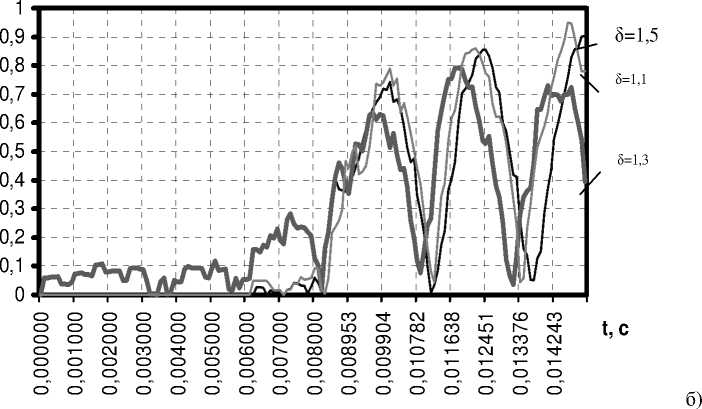
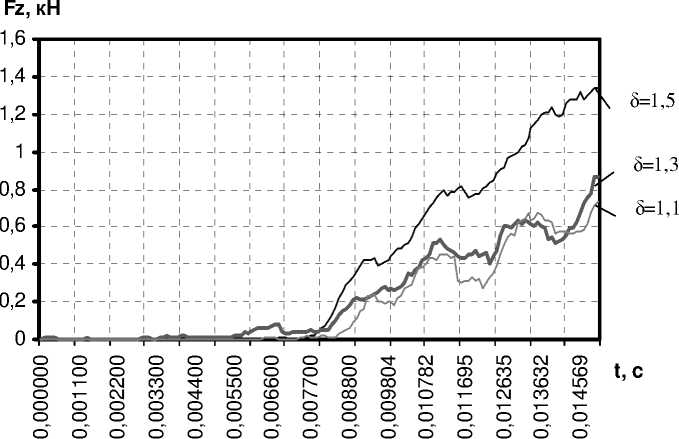
Рисунок 4 – Изменение сил , действующих на инструмент во времени t: а ) нормальной - F X , б ) продольной - F Y , в ) касательной - F Z

б )

Рисунок 5 – Распределение эквивалентных напряжений по М изесу , возникающих в материале заготовки :

а ) при δ =1,5; б ) при δ =1,3; в ) при δ =1,1

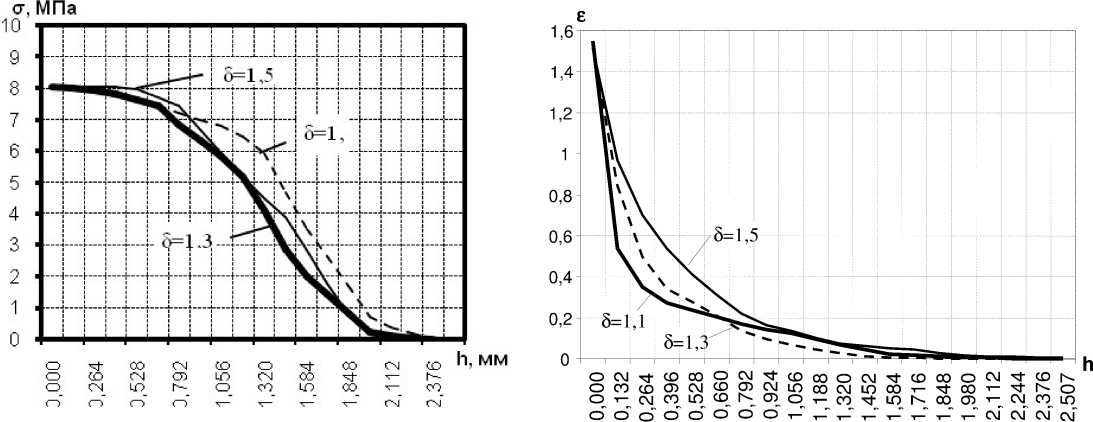
Рисунок 8 – Распределение эквивалентных деформаций по М изесу в вершине резьбы

Рисунок 6 – Распределение эквивалентных напряжений по М изесу , возникающих в вершине резьбы , по глубине h

• а )                                               б )                                                в )

Рисунок 7 – Распределение эквивалентных деформаций по М изесу в материале детали : а ) при δ =1,5; б ) при δ =1,3; в ) при δ =1,1