Моделирование показателей рыночной стоимости публичных компаний РФ c использованием метода главных компонент

В работах [1, 2], выполненных по данным финансовой отчетности 2012 г. публичных компаний нефинансового сектора РФ, было показано, что при моделировании капитализации и стоимости компаний их финансовые показатели (стоимость активов, собственный капитал, выручка и чистая прибыль) являются мультиколлинеарными факторами (линейный коэффициент корреляции r>0,8, коэффициент роста дисперсии VIF>5), что соответствует экономической природе данных показателей.

Мультиколлинеарность не позволяет одновременно включать эти финансовые показатели как факторы в уравнение регрессии, поэтому были построены однофакторные регрессионные модели вида:

LN ( Капитализация / Стоимость _ компании ) = B _o + B. • LN ( фактор )

, что для исходных показателей означает модель:

Капитализация / Стоимость _ компании = e B • фактора .

Кроме указанных выше факторов, в модели было учтено влияние отраслевой принадлежности компании с помощью dummy-переменных (базой является нефтегазовый сектор). Результаты оценки уравнений регрессии приведены в таблицах 1-2.

Таблица 1  – Результаты оценивания однофакторных линейно логарифмических моделей для отклика капитализация компании

Фактор	Констант а B 0 (значимая на уровне 0,05)	Коэффициент регрессии B 1 (коэффициен т эластичности )	Значимые на уровне 0,05 коэффициент ы для dummy	Коэффициент детерминаци и R2, %	Средняя относительна я ошибка модели (mape), %
Активы		1,245	-	76,9	13,0
Собственны й капитал	-2,162	1,207	-	77,4	12,3
Выручка	-2,263	1,191	-	73,2	13,7
Чистая	-	1,163	Энергетика=	98,6*	10,7

Фактор	Констант а B 0 (значимая на уровне 0,05)	Коэффициент регрессии B 1 (коэффициен т эластичности )	Значимые на уровне 0,05 коэффициент ы для dummy	Коэффициент детерминаци и R2, %	Средняя относительна я ошибка модели (mape), %
прибыль			1,532 Металлургия= 1,420 Другие= 1,379

*Для регрессии через начало координат (модель без свободного члена) R-квадрат показывает, какая доля вариабельности зависимой переменной относительно начала отсчета объясняется регрессией. Это НЕЛЬЗЯ применять к R2 для моделей, включающих в себя свободный член

Таблица 1  – Результаты оценивания однофакторных линейно логарифмических моделей для отклика стоимость компании

Фактор	Констант а B 0 (значима я на уровне 0,05)	Коэффициен т регрессии B 1 (коэффициен т эластичност и)	Значимые на уровне 0,05 коэффициенты для dummy	Коэффициен т детерминаци и R2, %	Средняя относительна я ошибка модели mape, %
Активы	-	,981	-	99,7*	4,8
Собственны й капитал	-	1,026	Другие=0,900	99,6*	5,1
Выручка	1,862	,863	Машиностроение -1,113 Химия и нефтехимия=-1,096	90,2	4,8
Чистая прибыль	4,702	,720	Машиностроение -1,235 Химия и нефтехимия= -1236	86,2	5,1

*Для регрессии через начало координат (модель без свободного члена) R-квадрат показывает, какая доля вариабельности зависимой переменной относительно начала отсчета объясняется регрессией. Это НЕЛЬЗЯ применять к R2 для моделей, включающих в себя свободный член

Для преодоления проблемы мультиколлинеарности, чтобы не удалять факторные переменные из регрессионных моделей, используем регрессионный анализ главных компонент [3]. Для его применения сначала необходимо воспользоваться факторным анализом (на основе метода главных компонент), чтобы «свернуть» указанные 4 фактора в новые переменные – главные компоненты, которые определяются как линейные функции фактических переменных. Результаты применения факторного анализа представлены ниже.

Таблица 3 – Результаты применения факторного анализа

KMO и критерий Бартлетта

Мера адекватности выборки Кайзера-Майера-Олкина (КМО). Критерий сферичности Бартлетта   Примерная Хи-квадрат ст.св. Знач.

,763 420,249 6 ,000

Объясненная совокупная дисперсия

Компонент	Начальные собственные значения			Суммы квадратов нагрузок извлечения
	Всего	% дисперсии	Суммарный %	Всего	% дисперсии	Суммарный %
1	3,823	95,578	95,578	3,823	95,578	95,578
2	,154	3,856	99,434
3	,020	,493	99,927
4	,003	,073	100,000

Метод выделения факторов: метод главных компонент.

Матрица компонентовa

	Компонент
	1
Стоимость активов, млн. дол.	,992
Собственный капитал, млн. дол.	,989
Выручка, млн. дол.	,939
Чистая прибыль, млн. дол.	,989

Метод выделения факторов: метод главных компонент.

a. Извлечено компонентов - 1.

Матрица коэффициентов значений компонентов

	Компонент
	1
Стоимость активов, млн. дол.	,259
Собственный капитал, млн. дол.	,259
Выручка, млн. дол.	,246
Чистая прибыль, млн. дол.	,259

Метод выделения факторов: метод главных компонент.

Оценки компонентов.

Результаты таблицы3 и график на рисунке 1 показывают, что данные факторы целесообразно «свернуть» в одно компоненту (только у первой компоненты собственное значение превышает 1). Мера адекватности (>0,5) и значимый на уровне 0,05 критерий сферичности Бартлетта говорят о применимости метода главных компонент к выбранным переменным.

Исходные переменные и новая компонента связаны очень тесно (коэффициенты корреляции каждой их исходных переменных и компоненты более 0,9). Новая компонента характеризует 95,6 % (более 70 %) вариации переменных.

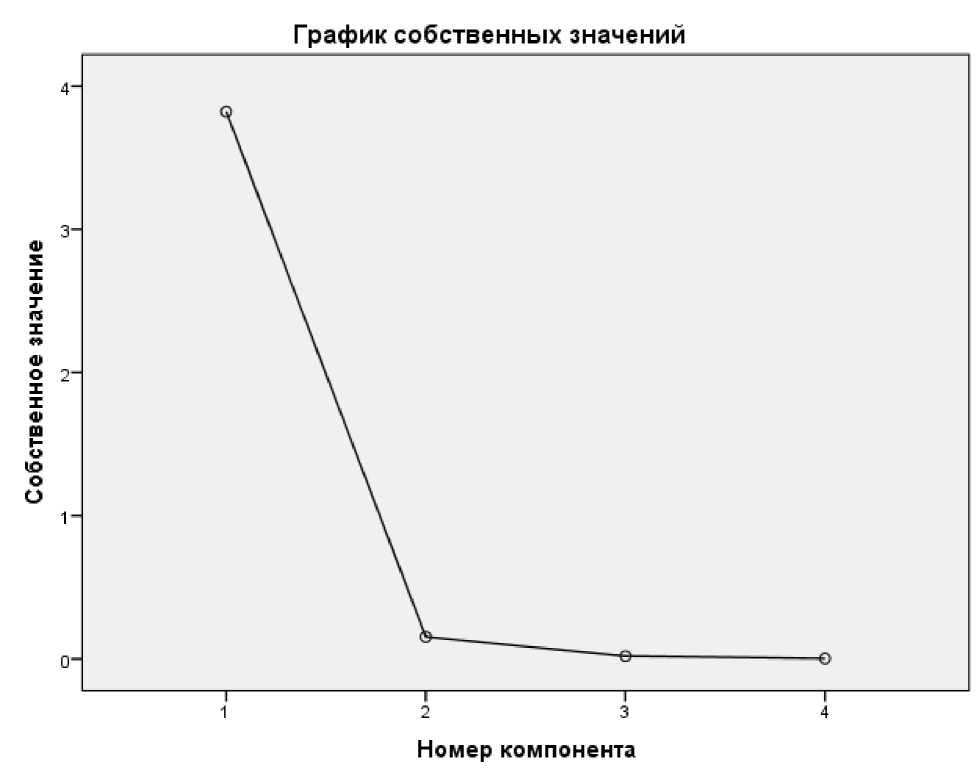
Рисунок 1 – График собственных значений компонент

Таким образом, методом факторного анализа получили новую компоненту, которая вычисляется следующим образом:

Компонента = 0,259СА + 0,259СК + 0,246В + 0,259ЧП,

где СА, СК, В, ЧП – z-стандартизованные значения соответственно стоимости активов, собственного капитала, выручки, чистой прибыли.

В дальнейшем были построены линейно-логарифмические модели капитализации и стоимости с новой факторной переменной, объединяющей в себе все 4 фактора и характеризующей одновременно как доходы, так и финансовые результаты компании. Для возможности логарифмирования компонента была преобразована в переменную F, принимающую только положительные значения:

F[ = Компонента/ + 0,4,

где Fi, Компонента^ - значения переменной F и компоненты соответственно у i-ой компании.

Результаты регрессионного моделирования представлены в таблице 4.

Таблица 4 – Результаты оценки линейной логарифмической модели

для отклика – капитализация компании Сводка для моделиb
Модель	R	R-квадрат	Скорректированный R-квадрат	Стандартная ошибка оценки
1	,894a	,800	,795	,96150
a. Предикторы: (константа), LN_F b. Зависимая переменная: LN_кап

ANOVAa

Модель	Сумма квадратов	ст.св.	Средний квадрат	F	Знач.
1       Регрессия Остаток Всего	155,265 38,828 194,093	1 42 43	155,265 ,924	167,949	,000b

a.    Зависимая переменная: LN_кап b.    Предикторы: (константа), LN_F Коэффициентыa
Модель	Нестандартизованные коэффициенты		Стандартизованные коэффициенты	т	Знач.	95,0% Доверительный интервал для B
	B	Стандартная Ошибка	Бета			Нижняя граница	Верхняя граница
1 (Константа) LN_F	10,730 1,483	,270 ,114	,894	39,770 12,960	,000 ,000	10,186 1,252	11,275 1,714

a. Зависимая переменная: LN_кап

Результаты таблицы 4 показывают, что получена адекватная модель (значимость F-критерия менее 0,05) вида:

LN ( к Капитализация ) = 10,730 + 1,483 • LN ( F ), или

Капитализация = 45706,692 • F^1,483

Данная адекватная модель характеризует 80,0 % общей вариации натурального логарифма капитализации. При увеличении компоненты F (это происходит, когда увеличиваются значения всех исходных факторов) на 1 % капитализация в среднем увеличивается на 1,5 % (с вероятностью 0,95 на 1,3 – 1,7 %). Средняя относительная ошибка модели MAPE=10,2 %. Остатки модели соответствуют требованиям закона нормального распределения (критерий значимости теста Шапиро-Уилка 0,139>0,05) и независимости от теоретических значений (значимость линейного коэффициента корреляции между остатками и теоретическими значениями отклика равна 1,000).

Аналогичные модели капитализации были построены для каждого года в период 2004-2011. Сравнение коэффициентов регрессии B 1 на основе значений доверительных интервалов показало, что на уровне значимости 0,05 имеются отличия в значениях коэффициента в модели для 2012 года и в моделях для 2004-2007, а также 2010 гг.: коэффициенты регрессии, характеризующие эластичность капитализации от главной компоненты, в эти периоды меньше (не превосходят 1 %), чем в 2012 г. Степень тесноты линейной взаимосвязи главной компоненты и капитализации, которая характеризуется коэффициентом корреляции (для 2012 г. коэффициент корреляции r=0,894, см. таблицу 4), не различается в период 2004-2012 гг. (для проверки значимости различий между двумя коэффициентами корреляции на уровне значимости 0,05 используется критерий ^γ , который сравнивается с квантилем стандартного нормального распределения [4]).

Таблица 5 – Результаты оценки линейной логарифмической модели для отклика – стоимость компании

Сводка для моделиb

Модель R R-квадрат Скорректированный R-квадрат Стандартная ошибка оценки 1 ,948a ,898 ,895 ,52405 a. Предикторы: (константа), LN_F b. Зависимая переменная: LN_стоим

ANOVAa

Модель Сумма квадратов ст.св. Средний квадрат F Знач. 1       Регрессия 101,391 1 101,391 369,198 ,000b Остаток 11,534 42 ,275 Всего 112,925 43 a. Зависимая переменная: LN_стоим b. Предикторы: (константа), LN_F

Коэффициентыa

Модель	Нестандартизованные коэффициенты		Стандартизованные коэффициенты	т	Знач.	95,0% Доверительный интервал для B
	B	Стандартная Ошибка	Бета			Нижняя граница	Верхняя граница

1 (Константа) LN_F 11,078 1,198 ,147 ,062 ,948 75,335 19,215 ,000 ,000 10,781 1,073 11,375 1,324 a. Зависимая переменная: LN_стоим

Результаты говорят о том, что получена адекватная модель вида:

LN (Стоимость _ компании ) = 11,078 + 1,198 • LN (F), или

Стоимость компании = 64731,291 F^1,198 ^^^™

Данная модель характеризует 89,8% общей вариации натурального логарифма стоимости компании. При увеличении компоненты F на 1 % стоимость компании в среднем увеличивается на 1,2 % (с вероятностью 0,95 на 1,1 – 1,3 %). Средняя относительная ошибка модели MAPE=4,5 %. Остатки модели соответствуют требованиям закона нормального распределения (критерий значимости теста Шапиро-Уилка 0,644>0,05) и независимости от теоретических значений (значимость линейного коэффициента корреляции 1,000).

Аналогичные модели стоимости компании были построены для каждого года в период 2004-2011. Сравнение коэффициентов регрессии B 1 на основе значений доверительных интервалов показало, что на уровне значимости 0,05 имеются отличия в значениях коэффициента в модели для 2012 года и в моделях для 2004-2007, 2010 гг.: коэффициенты регрессии, характеризующие эластичность стоимости компании от главной компоненты в эти периоды, меньше (не превосходят 1 %), чем в 2012 г. Степень тесноты линейной взаимосвязи главной компоненты и капитализации, которая характеризуется коэффициентом корреляции (для 2012 г. коэффициент корреляции r=0,948, см. таблицу 5) не различается в период 2004-2012 гг.

Отраслевая принадлежность компании и статус «голубой фишки» не влияют на капитализацию (коэффициенты регрессии при соответствующих dummy-переменных не являются значимыми на уровне 0,05). Но отраслевая принадлежность влияет на стоимость компании в 2012 г., результаты оценки регрессионной модели с dummy-переменными представлены в таблице 6.

Данная адекватная модель характеризует 92,2% общей вариации натурального логарифма стоимости компании. При увеличении компоненты F на 1 % стоимость компании в среднем увеличивается на 1,2 %. Средняя относительная ошибка модели MAPE=4,1 %. Отраслевая принадлежность компании влияет на ее стоимость, но различия проявляются только для металлургических компаний: при прочих равных условиях стоимость 0,858

металлургической компании будет в e     , раза выше, чем у компании нефтегазовой отрасли, стоимость компаний других отраслей значимо не отличается от нефтегазовой.

Несмотря на адекватность и практическую пригодность (коэффициент детерминации R2=0,800) регрессионной модели капитализации, при использовании данной модели для прогнозирования капитализации публичных нефинансовых компаний России по данным 2013 г. получена систематическая ошибка – завышение капитализации по сравнению с фактическими данными для всех компаний выборки 2013 г. Это свидетельствует о том, что такой рыночный показатель компании как капитализация зависит не только от внутренних факторов – ее доходов и финансовых результатов, но и от внешних – макроэкономических. Одновременное влияние внутренних и внешних факторов можно проанализировать и смоделировать только на основе панельных (пространственно-временных) моделей.

Таблица 6 – Результаты оценки линейной логарифмической модели с dummy-переменными отраслевой принадлежности для отклика – стоимость компании

Введенные/удаленные переменныеa
Модель		Введенные переменные		Удаленные переменные			Метод
1		Другие, Машиностроение, Химия и нефтехимия, LN_F, Металлургия, Энергетикаb		.			Enter
a.    Зависимая переменная: LN_стоим b.    Все требуемые переменные введены. Сводка для моделиb
Модель	R		R-квадрат		Скорректированный R-квадрат	Стандартная ошибка оценки
1	,960a		,922		,909	,48752

a. Предикторы: (константа), Другие, Машиностроение, Химия и нефтехимия, LN_F, Металлургия, Энергетика b. Зависимая переменная: LN_стоим

ANOVAa

Модель Сумма квадратов ст.св. Средний квадрат F Знач. 1     Регрессия 104,131 6 17,355 73,019 ,000b Остаток 8,794 37 ,238 Всего 112,925 43 a. Зависимая переменная: LN_стоим b. Предикторы: (константа), Другие, Машиностроение, Химия и нефтехимия, LN_F, Металлургия, Энергетика

Коэффициентыa
Модель	Нестандартизованные коэффициенты	Стандартизованны е коэффициенты	т	Знач .	95,0% Доверительный интервал для B

B Стандартна я Ошибка Бета Нижня я границ а Верхня я граница 1 (Константа) 10,764 ,221 48,76 3 ,000 10,317 11,211 LN_F 1,234 ,084 ,976 14,61 0 ,000 1,063 1,405 Энергетика ,333 ,344 ,101 ,971 ,338 -,363 1,029 Металлургия ,858 ,337 ,184 2,550 ,015 ,176 1,540 Машиностроени е ,125 ,447 ,020 ,279 ,782 -,782 1,031 Химия и нефтехимия ,159 ,406 ,029 ,392 ,698 -,663 ,981 Другие ,564 ,360 ,142 1,567 ,126 -,165 1,294 a. Зависимая переменная: LN_стоим