Моделирование полей упругих деформаций с применением метода точечных источников

Введение. Расчет полей упругих напряжений в деформированных телах является одной из важнейших задач прикладной механики и математики [1–3]. При численном решении этих задач в зависимости от их конкретных особенностей применяют различные численные методы. Довольно часто используются методы конечных разностей (МКР) [4] и граничных элементов (МГЭ) [3]. Однако особое место занимает метод конечных элементов (МКЭ) [2], который по праву можно считать эталоном для численного решения краевых задач математической физики. Тем не менее в ряде

случаев, в том числе при моделировании полей упругих напряжений в деформированных твердых телах, использование МКЭ может оказаться неэффективным. Например, МКЭ не всегда обеспечивает требуемую высокую точность результата, особенно в тех случаях, когда необходимо найти производную от искомой функции, вычисление которой производится путем численного дифференцирования, что приводит к резкому увеличению погрешности вычислений. Кроме того, МКЭ может оказаться недостаточно быстродействующим, если необходимо получать решение в режиме реального времени. Таким образом, возникает необходимость поиска численных методов, позволяющих получать более точное решение за более короткий промежуток времени. В этом смысле представляет интерес метод точечных источников поля (МТИ) [5–12]. Он может использоваться для решения широкого круга задач математической физики. Наиболее эффективно использование этого метода при решении краевых задач для уравнений эллиптического типа: уравнений Лапласа, Гельмгольца, бигармонических уравнений [8, 13]. Имеются сведения о возможности и эффективности использования этого метода при решении краевых задач для уравнений параболического типа и для волновых уравнений [8, 14]. В данной статье иллюстрируется возможность применения МТИ при моделировании полей упругих напряжений в деформированных твердых телах. Прежде всего дадим краткое описание МТИ.

Краткое описание МТИ. Пусть в n -мерном Евклидовом пространстве задана область V , ограниченная поверхностью S . В области V определено однородное линейное дифференциальное уравнение в частных производных

L U = 0 ,                                                    (1)

а на граничной поверхности (на граничном контуре – для двумерного случая) S задано условие

U\_s = f ,                                                   (2)

где L ^ˆ и l ^ˆ — линейные операторы, f — заданная функция, U — искомый потенциал поля.

Пусть определена система ф, линейно независимых решений уравнения (1). Тогда приближенное решение граничной задачи (1)–(2) можно искать в виде

N

U ( r ) ” Z «/ Ф 1 ( r ) .                                                     ⁽³⁾

i = 1

Для нахождения неизвестных коэффициентов a подставляем (3) в граничное условие (2) и потребуем его выполнения в N узловых точках r j . В результате для нахождения коэффициентов a i получается система линейных уравнений

N

Z « А( r j ) = f ( r j ) .                                              ⁽⁴⁾

= 1

В качестве системы функций ф_; можно использовать фундаментальные решения ф, =ф ( r , R ,) уравнения (1), соответствующие точкам R i , расположенным на вспомогательной замкнутой поверхности S q , целиком охватывающей S и не имеющей с ней (и с V ) общих точек. В [5] показано, что при выполнении достаточно общих условий система функций ф ( r , R_i ) будет обладать свойствами линейной независимости и полноты, поэтому ее можно использовать для нахождения приближенного решения граничной задачи (1)–(2) в виде суммы

N un (r )~Z q^(r,R).                                     (5)

= 1

Механика

Фундаментальное решение J ( r, R ) можно рассматривать (по аналогии с потенциальными электрическими полями) как потенциал поля, созданного в точке r единичным положительным «зарядом», помещенным в точку R, а искомое решение, созданное протяженными, непрерывно распределенными зарядами, представлять в виде суперпозиции полей точечных зарядов. Коэффициенты q в (5) при этом можно рассматривать как величины точечных зарядов, расположенных на поверхности S q . Заряды q назовем моделирующими зарядами. Такое физическое истолкование решения граничной задачи способствует удачному выбору вспомогательной поверхности S q и оптимальному расположению на ней зарядов, что существенно при численном решении. Таким образом, решение краевой задачи сводится к решению системы линейных уравнений

N

Z qM( r j , R ) = f ( r j ) .                                                ⁽⁶⁾

= 1

После решения системы (6), называемой системой МТИ, и нахождения зарядов q искомое приближенное решение краевой задачи вычисляется с помощью формулы (5).

В работах [7, 8, 12] показывается, что погрешность МТИ е при решении краевых задач для уравнения Лапласа экспоненциально быстро убывает с ростом числа зарядов, моделирующих искомое поле. Например, для круговой области решения радиусом r 0 , если заряды располагаются на вспомогательной окружности радиусом R , то

N /2

e = E -0- l R

.                                                                          (7)

Здесь Е — параметр, не зависящий от числа зарядов, моделирующих поле.

Моделирование упругих деформаций. Плоские упругие деформации в изотропных телах определяются вектором деформаций, компоненты которого U x ( x,y ) и U y ( x,y ), как известно, удовлетворяют системе двух линейных уравнений эллиптического типа [5, 15]:

(Х + ц)|^ + цАUx = 0, (Х + ц) — + цАUy = 0,(8)

где λ и μ — постоянные Ламе, o d Ud

6 =     + dx5

Пусть на границе S деформированного твердого тела V выполняются граничные условия a U + a U +B ст +B ст = f , a U + a U +B ст +B ст = f .(9)

xx x      xy y     xx nx     xy ny      x , yx x      yy y      yx nx     yy nyy

Здесь a, в, / (с соответствующими индексами) — известные функции точки (x, y) е V . ст^ , ст — компоненты вектора напряжений; ст„ = стхcoss (n, x ) + ст^ cos (n, y), ст^ = ст cos (n, y ) + ct, cos (n, x); cos (n, x), cos (n, y) — направ ляющие косинусы внешней нормали границы S в данной ее точке.

ст Л6.2^^Ux , ст    Л6. 2 JU, ст               + U 1.(10)

dx                   dy     x-    y ' l dyd

Классические первая и вторая граничные задачи теории упругости, когда на границе S заданы либо напряжения, либо смещения, являются частными случаями граничной задачи (8)–(9) при соответствующих значениях параметров α и β.

При моделировании двумерных упругих деформаций используются фундаментальные решения для каждой из двух компонент (x, y) вектора U(r). Причем каждой компоненте соответствуют два типа фундаментальных решений и, следовательно, два типа зарядов, моделирующих поле упругих деформаций. Важнейшим параметром фундамен- тального решения является также координата точки, в которой располагается заряд, создающий поле упругих дефор- маций. При решении задач теории упругости с помощью МТИ моделирующие заряды располагаются в узловых точ- ках Ri (с координатами Xi, Yi; здесь i — номер заряда), расположенных на вспомогательном замкнутом контуре Sq, целиком охватывающем S и не имеющем с ним (и с V) общих точек. Таким образом, фундаментальные решения опреде- ляются тремя параметрами: i — номер узловой точки, j — тип фундаментального решения и заряда (1 или 2) и k — тип компоненты смещения (x или y). Эти фундаментальные решения имеют вид

0 l x ( r ) =

- n ln | r - R | +

d r-R J d X i

, i y ( _r ) = ^d r ^- R i । ^d V ^- R i । . i ^k ’    d X     d Y    ’

ф 2 x ( r ) =

5 V - R | 5 V - R| 5 X   5 Y

^ф 2 ^y ( ^r ) = ^{- n ln} r ^- R -| +

f d| r - R | У l ^d Y   J

Здесь n = ( Х + 3 ц ) / ( Х + ц ) .

В соответствии с формулами (11) единичный положительный заряд поля смещений первого типа создает в точке своего нахождения бесконечно большое смещение вдоль оси x . При этом в точке, отстоящей от заряда в направлении оси x на единичное расстояние, возникает смещение вдоль оси x единичной величины. Напротив, единичный положительный заряд поля смещений второго типа создает в точке своего нахождения бесконечно большое смещение вдоль оси y . При этом в точке, отстоящей от заряда в направлении оси y на единичное расстояние, возникает смещение вдоль оси y единичной величины.

Полнота системы функций (11), доказанная в [5], позволяет решать граничную задачу (8), (9) с помощью МТИ. Для этого необходимо найти заряды, моделирующие искомое поле упругих напряжений и деформаций путем решения системы МТИ, конкретный вид которой зависит от граничных условий решаемой задачи. Имеются сведения

о применении МТИ к решению задач теории упругости [5]. Однако следует признать, что в настоящее время проблема использования МТИ для моделирования упругих деформаций в твердых телах разработана весьма слабо.

Рассмотрим первую граничную задачу теории упругости, когда на границе S заданы смещения U x и U y . Эта задача соответствует частному, простейшему случаю граничных условий (9), которые принимают вид

U x l s = f x • U y\s = f y ^.                                       (12)

Возможны различные варианты построения системы МТИ. Наиболее естественно предположить, что для моделирования упругих деформаций целесообразно использовать одинаковое число N зарядов первого типа q ¹ (которым соответствуют фундаментальные решения ф ^{1 x} и ф ¹ y ) и зарядов второго типа q ² (которым соответствуют фундаментальные решения ф ^{2 x} и ф ² y ). Пусть первые N зарядов — заряды первого типа, а последующие N зарядов — заряды второго типа. Учитывая это, в обозначении зарядов можно не указывать их тип, который теперь будет определяться номером заряда.

Положение зарядов, как отмечалось выше, соответствует точкам R i , расположенным на вспомогательном контуре S q , целиком охватывающем S . Количество таких точек равно 2 N . Разместим на границе S точки коллокации числом 2 N . В этих точках требуем выполнение граничных условий (12). Теперь систему МТИ (точнее, уравнение системы с номером j ) можно записать по аналогии с (6) в виде

Z q i t ji = fj ^или i = 1

N 2 N

Zqi^r(rj)+ Z qiф2x(rj)=fx(rj)для j-N;

i=1

N 2 N

Z q .^iy ( r j ) ⁺ Z q ^ ² y ( r j ) = ^f y ( r j ) ^{для j} >  ^N .

i=1

Здесь использованы следующие обозначения:

для j <  N  f j = f x ( r j ) , ф ji = ф ^{1 х} ( r j ) , если i <  ^N , и ф ji = ф ^{2 x} ( r j ) , ^если i >  ^N ;

для j >  N  f j = f y ( r j ) , ф л = ф ^{1 у} ( r j ) , если i <  N , и ф л = ф ² y ( r j ) , если i >  N.

После решения системы (13) и нахождения зарядов q приближенные значения поля смещений в объеме деформированного тела вычисляются с помощью формул

N 2 N

U x ( r ) ~ Z q i^ix ( r )⁺ Z q i^ф 2 ^x ( r ) ,                                           ⁽¹⁴⁾

• i = 1                   i = N + 1

N 2 N

Uy (r) ” Z qi^y (r)+ Z »<ф 2 y (r).

• i = 1                   i = N + 1

Затем, используя формулы (10), можно вычислить компоненты тензора деформаций. При этом, как отмечалось выше, дополнительной численной ошибки не возникает.

Аналогичным образом решаются вторая граничная задача теории упругости или смешанная граничная задача — когда на одной части границы заданы смещения, а на другой — напряжения. В этом случае вид системы МТИ (13) изменяется.

Решение стандартной задачи МТИ для полей упругих деформаций. Важнейшей задачей исследования численного метода, в том числе и МТИ, является оценка погрешности решения, полученного с помощью этого метода, а также установление зависимости погрешности от параметров задачи, например, от геометрических характеристик области решения, от числа зарядов, моделирующих поле, от их расположения вокруг области решения и т. д. В общем случае получить удовлетворительное решение этой задачи весьма затруднительно. Поэтому исследование данной проблемы начнется с простейших случаев МТИ с последующим усложнением задачи.

Механика

В ряде публикаций производится оценка погрешности МТИ при решении задачи Дирихле для круговой области [8–13]. Эту задачу назовем стандартной задачей МТИ. Приведем здесь результаты анализа ее численного решения.

Так как любое поле упругих деформаций, ввиду линейности уравнений (11), обладает свойством суперпозиции, то его можно представить в виде суперпозиции полей точечных источников. Поэтому при исследовании погрешности МТИ важнейшее значение имеет задача нахождения поля, созданного одним точечным зарядом, и оценка погрешности для этого поля.

Пусть искомое поле есть поле смещения, созданное единичным положительным зарядом первого типа, помещенным в точку с радиус-вектором ρ и координатами (ρ, 0). Тогда в соответствии с (11) искомое поле будет описываться соотношениями

² x -P I I ^{, U}y r ^- P|J y

^Ux ( ^Г ) = ^- n ln | r ^-P| +

( r ) =

( ^{x -} p ) y I ^r -Pl ²

.

Область решения представляет собой окружность радиусом r 0 = 2. Заряды, моделирующие искомое поле, равномерно располагаются на вспомогательной окружности радиусом R . Количество зарядов каждого типа полагается равным N . Полное число зарядов N q = 2 N . Аналогично на границе области решения S , т. е. на окружности радиусом r 0 равномерно располагаются узловые точки, точки коллокации. Полное число зарядов и точек коллокации может не совпадать [8]. Однако здесь применяется наиболее часто используемый и проверенный вариант МТИ, когда каждому заряду на вспомогательной окружности соответствует заряд на границе S . При этом допускается совпадение положения зарядов первого и второго типов и соответствующих им точек коллокации. Здесь при проведении численных экспериментов положения зарядов обоих типов и точек коллокации соответствовали полярным координатам

V = 2 n ( i - 1 ) / N , 1 <  i <  N .

Погрешность МТИ в каждой точке области решения граничной задачи определяется величиной

^E ( r ) = max (| ^£ x ( Г )| ,| ^£ y ( Г )| ) , где £ x ( Г ) = U x ( Г )^- u_x ( Г ) , £ y ( Г ) = U y ( Г )^- U y ( Г ) .

Так как функции Ux (r), ux (r), Uy (r), u (r) удовлетворяют однородным эллиптическим уравнениям (8), то и функции Ex (r), Ex (r) также удовлетворяют этим уравнениям, а, следовательно, своего максимального и минимального значения достигают на границе S. Поэтому в качестве относительной погрешности МТИ может использоваться величина e = £max-,                                                         (16)

umax где Emax =£( г )|s , U max = maX (| Ux (r )| , |Uy (r )|)|$ •

Ниже анализируются результаты численных экспериментов при исследовании погрешности МТИ от различных параметров задачи. На рис. 1 приведены графики зависимости относительной погрешности МТИ e от количества зарядов первого типа N (равного количеству зарядов второго типа). При расчетах полагалось, что искомое поле — это поле точечного заряда первого типа, расположенного на оси х , удаленной от центра области V на расстояние ρ = 2 r 0 . Тонкая сплошная линия на рис. 1 рассчитана при радиусе вспомогательной окружности R = 1,1 r 0 . На рис. 1 представлены также зависимости, рассчитанные при R = 1,3 r 0 (жирная сплошная линия) и при R = 1,7 r 0 (пунктирная линия).

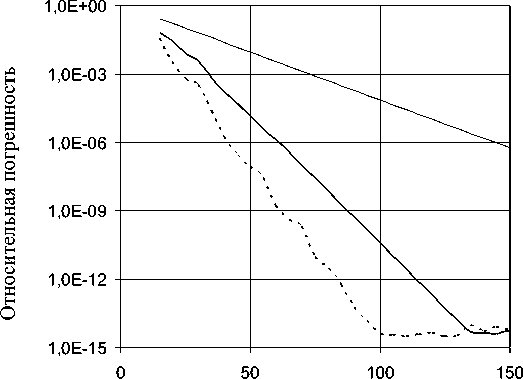
Количество зарядов (N)

Рис. 1. Зависимость погрешности МТИ от количества зарядов, моделирующих искомое поле для разных значений R

Из рис. 1 видно, что погрешность МТИ убывает с ростом числа зарядов по экспоненциальному закону. Это качественно согласуется с полученной теоретически формулой оценки погрешности МТИ при решении задачи Дирихле для уравнения Лапласа (7). Наблюдается не только качественное, но и некоторое количественное соответствие формуле (7) погрешности данных, представленных на рис. 1. Например, зависимость погрешности от числа зарядов,

(1 11,01 Nq соответствующая значению R =1,1 ro (тонкая сплошная линия), аппроксимируется формулой e = 1,09         . Для

1 1,1 7

значений R = 1,3 r 0 (жирная сплошная линия) и R = 1,7 r 0 (пунктирная линия) это соответствие хотя и в меньшей степени

NN 0,964 ^q                                                      0,659 ^q

[ 1 1 ,2                        ( 1 1 ,2

также наблюдается: при R = 1,3 r о e = 2,914 1 — I      ; при R = 1,3 r о e = 6,598 1 — I      . Необходимо, однако, отме-

\ 1,3 7                                      \ 1,⁷ 7

тить, что количественное согласие с формулой (7) наблюдается только в том случае, если искомое поле создается зарядами, достаточно удаленными от границы S области решения, например на ρ > 2 r 0 . Если поле создается зарядами, расположенными вблизи границы S области решения, то экспоненциальная зависимость погрешности численного решения от числа зарядов N сохраняется, но при этом может измениться коэффициент перед параметром N в показателе степени в формуле (7) с 0,5 на меньшее значение.

Экспоненциально быстрое уменьшение погрешности численного решения с ростом числа зарядов N продолжается до некоторого значения N = N max , при котором погрешность МТИ достигает минимального значения e min . При N > N max дальнейшее снижение погрешности прекращается и может смениться медленным ее ростом. Как видно из рис. 1, при R = 1,3 r 0 N max = 135 e min = 5·10^–15; при R = 1,7 r 0 N max = 100 e min = 4·10^–15.

Значения величин e min и (в меньшей степени) N max зависят не только от отношения^. R / r 0 , но и от самого моделируемого поля, в данном случае от величины параметра ρ. Эту особенность численного решения, полученного с помощью МТИ, иллюстрирует рис. 2. На нем представлены графики зависимости относительной погрешности МТИ e от количества зарядов первого типа N , построенные при различных значениях параметра ρ:

— при ρ = 1,2 r 0 (тонкая сплошная линия);

— при ρ = 1,5 r 0 (жирная сплошная линия);

— при ρ = 2 r 0 (пунктирная линия).

Механика

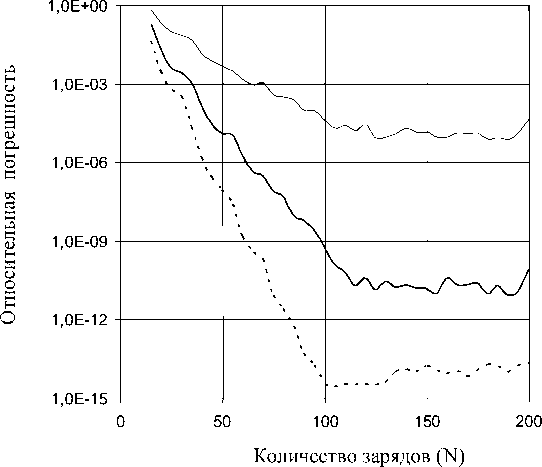
Рис. 2. Зависимость погрешности МТИ от количества зарядов, моделирующих искомое поле, для разных значений ρ

Вычисления проводились при радиусе вспомогательной окружности R = 1,7 r 0 . Как видно из рис. 2: — при ρ = 1,2 r 0 e min = 7,5·10^–6;

— при ρ = 1,5 r 0 e min = 8·10^–12,

— при ρ = 2 r 0 e min = 4·10^–15.

Значения N max при этом близки к 100 и возрастают при переходе от больших ρ к меньшим.

При решении задач теории упругости необходимо учитывать, что одним из основных параметров, определяющих точность численного решения, является удаленность зарядов, моделирующих искомое поле, от границы области решения. В данном случае при решении стандартной задачи МТИ этим параметром является R . На рис. 3 приведены графики зависимости относительной погрешности МТИ e от относительной удаленности зарядов, моделирующих поле, равной Δ R = ( R – r 0 )/ r 0 . Зависимости, представленные на рис. 3, получены при ρ = 2 r 0 и трех различных значениях N :

— при N = 50 (тонкая сплошная линия);

— при N = 75 (жирная сплошная линия);

— при N = 125 (пунктирная линия).

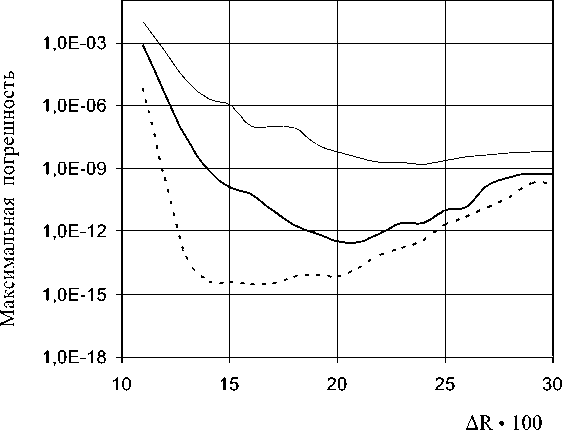
Рис. 3. Зависимость погрешности МТИ от относительной удаленности Δ R зарядов от границы области решения

Из рис. 3 видно, что график зависимости погрешности МТИ от относительной удаленности зарядов, моделирующих искомое поле, от границы области решения представляет собой кривую с минимумом, который наблюдается при относительной удаленности Δ R min , причем при малых Δ R погрешность е убывает с ростом Δ R по экспоненциальному закону. Однако при дальнейшем росте Δ R убывание погрешности замедляется, и при Δ R = Δ R min погрешность МТИ достигает минимального значения e = e min . При дальнейшем росте Δ R погрешность МТИ медленно возрастает. Значения величин Δ R min и e min зависят от количества N . Чем больше N , тем меньше e min и Δ R min . Эта особенность численного решения задач упругости с помощью МТИ позволяет подбирать оптимальные значения параметров МТИ, обеспечивающие наименьшее значение погрешности решения.

Для МТИ характерно экспоненциально быстрое возрастание числа обусловленности системы МТИ С с ростом размерности системы, т. е. с увеличением числа моделирующих зарядов N [7]. Эту особенность МТИ при решении задач теории упругости иллюстрирует рис. 4, на котором представлены зависимости числа обусловленности системы МТИ с увеличением числа моделирующих зарядов N .

Графики на рис. 4 построены при тех же параметрах МТИ, что и графики на рис. 1, т. е. при ρ = 2 r 0 :

— R = 1,1 r 0 (тонкая сплошная линия);

— R = 1,3 r 0 (жирная сплошная линия);

— R = 1,7 r 0 (пунктирная линия).

Из рис. 4 видно, что число обусловленности системы МТИ С может изменяться в весьма широком интервале — от нескольких единиц до 1020 и более. Так как отдельные вычислительные операции не могут быть выполнены на компьютере абсолютно точно, а производятся с относительной погрешностью ε, то при решении системы МТИ возникает относительная погрешность округления e≤Cε.

Погрешность ε, обусловленная ограниченностью представления вещественных чисел на компьютере, при использовании чисел типа double имеет значение порядка 10–15. Это предельная точность вычислений на компьютере. В некоторых случаях при моделировании полей упругих деформаций с помощью МТИ эта предельно высокая точность

вычислений может быть достигнута. Например, как видно из рис. 1, при моделировании поля точечного заряда упругих смещений для ρ =2 r 0 предельная точность достигается при N >  135 для R = 1,3 r 0 и при N >  100 для R = 1,7 r 0 . Следует отметить, что такая высокая точность вычислений достигается, несмотря на большие значения чисел обусловленности (С > 10¹¹ для R = 1,3 r 0 и С > 10¹⁵ для R = 1,3 r 0 ). Такая ситуация является типичной для МТИ. При использовании МТИ точность результата может быть весьма высокой, несмотря на большие значения чисел обусловленности. Более того, весьма часто отмечается следующая особенность [20–22]: чем больше число обусловленности, тем выше точность результата. В ряде публикаций исследуются причины данной закономерности [21]. Тем не менее большие значения чисел обусловленности системы МТИ могут приводить к серьезному снижению точности результата. Именно этим в значительной степени объясняются относительно высокие погрешности при малых ρ (см. рис. 2) и R (см. рис. 3). Этим также объясняется некоторая немонотонность и слабые колебания представленных на рис. 1–3 зависимостей.

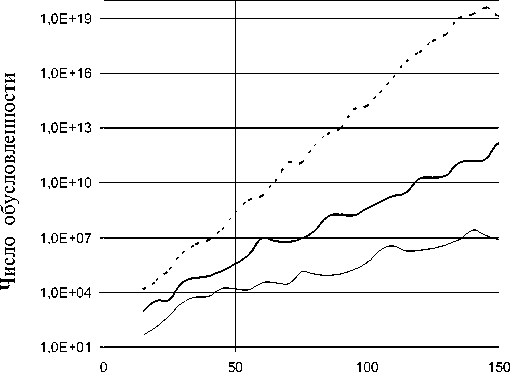
Количество зарядов (N)

Рис. 4. Зависимость числа обусловленности системы МТИ от количества зарядов, моделирующих искомое поле

Заключение. Проведенные исследования показали принципиальную возможность использования МТИ при моделировании полей упругих деформаций в твердом теле. Исследована зависимость погрешности от параметров системы при решении стандартной задачи МТИ. Полученные результаты качественно (и частично количественно) соответствуют результатам решения задачи Дирихле, а также задачи Неймана и третьей краевой задачи. Это показали дополнительные численные эксперименты.

При практической реализации МТИ необходимо подобрать наиболее эффективное значение удаленности Δ R моделирующих зарядов от границы области решения. Здесь следует учитывать, что чем ближе моделирующие заряды к границе, тем выше погрешность МТИ, но зато меньше число обусловленности системы МТИ и, соответственно, устойчивее решение. Напротив, с удалением моделирующих зарядов от границы области решения точность МТИ повышается, но одновременно увеличивается значение числа обусловленности системы МТИ, что может привести к повышению результирующей погрешности и даже к появлению неустойчивости решения. Наиболее эффективное значение удаленности Δ R можно подобрать в ходе численного эксперимента, начав, например, со значения Δ R = 0,3 r 0 .