Моделирование полета пассажирского самолета в вихревом следе

В последнее время наблюдается рост трафика, воздушных перевозок. Для увеличения пропускной способности вводят дополнительные эшелоны с уменьшенным расстоянием по высоте. В совокупности с увеличением среднего веса, самолета, это делает моделирование попадания пассажирского самолета, в турбулентный след другого тяжелого самолета, весьма, актуальной проблемой. Неправильное поведение летчика в данной ситуации может повлечь неприятные последствия, вплоть до аварии. Создание математических моделей движения самолета в спутной турбулентности и отработка их летчиками на пилотажных стендах является востребованной задачей.

2.    Физическое описание спутного следа за крупным самолетом

Время существования вихревго следа, за. самолетом-генератором зависит от его размаха. L и степени турбулентности атмосферы q. Чем больше его вес G, тем дольше существует порождаемый им вихревой след. Чем выше q, тем быстрее происходит диссипация вихревого следа, и тем меньше время его жизни. В крейсерском режиме полета, эволюция вихревого следа за самолетом претерпевает три стадии:

«Московский физико-технический институт (национальный исследовательский университет)», 2020

• 1)    Слияние одинаково закрученных вихрей, сбегающих с крыла, в два слабоизогнутых вихревых жгута.

• 2)    Изменение вихревыми жгутами своей формы из-за длинноволновых синусоидальных возмущений. Амплитуда возмущений при удалении от самолета растет. После этого происходит пересечение вихрей и образование вихревых колец.

• 3)    Разрушение вихревых колец и их полная диссипация. Вихревой след представляет опасность для другого самолета только до этапа разрушения вихревых колец.

3.    Математическая модель вихревого следа

На рис. 1 изображены вихревые жгуты за самолетом-генератором, летящим вдоль оси ОХ со скоростью V. Начало системы координат совпадает с центром масс самолета-генератора.

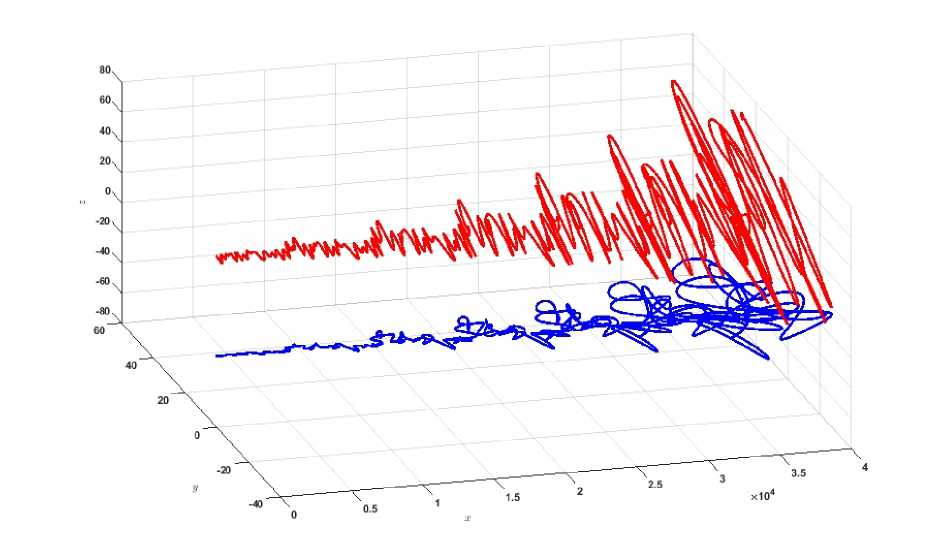
Рис. 1. Вихревые нити за самолетом в системе координат OXYZ

В данной работе была использована двухвихревая модель с учетом собранных статистических данных и основанная на законе сохранения момента импульса [2].

На расстоянии около 10 размахов от самолета-генератора вихревой след представляет собой два вихревых жгута, интенсивность которых можно оценить по формуле

Г

G

⁰ = IVb

а расстояние между ними b ~ 4L.

Согласно имеющимся экспериментальным данным, циркуляция вихревых жгутов уменьшается при удалении от самолета-генератора, что связано в первую очередь с диссипацией энергии. Для изменения циркуляции вихревых жгутов r(t) и размера ядра Гу(t) используется двухфазная модель диффузии вихря в турбулентной атмосфере:

r(t) =

(Го exp(-£), t < tSF, t E [tSF, 1.2tSF],

1Г0 exp(-^ДЩ)(1 - L2tSF—SF)> rv (t) = 1 + 0.35Д1 + 0.327t, где tS F = TSF • 2р^2 - момент времени переключения медленной фазы изменения циркуляции на быструю, TSF Е [2,8] - безразмерный показатель степени турбулентности атмосферы, t = ^7. Зависимость циркуляции Г и радиуса ту вихревых жгутов от времени приведены на рис. 2.

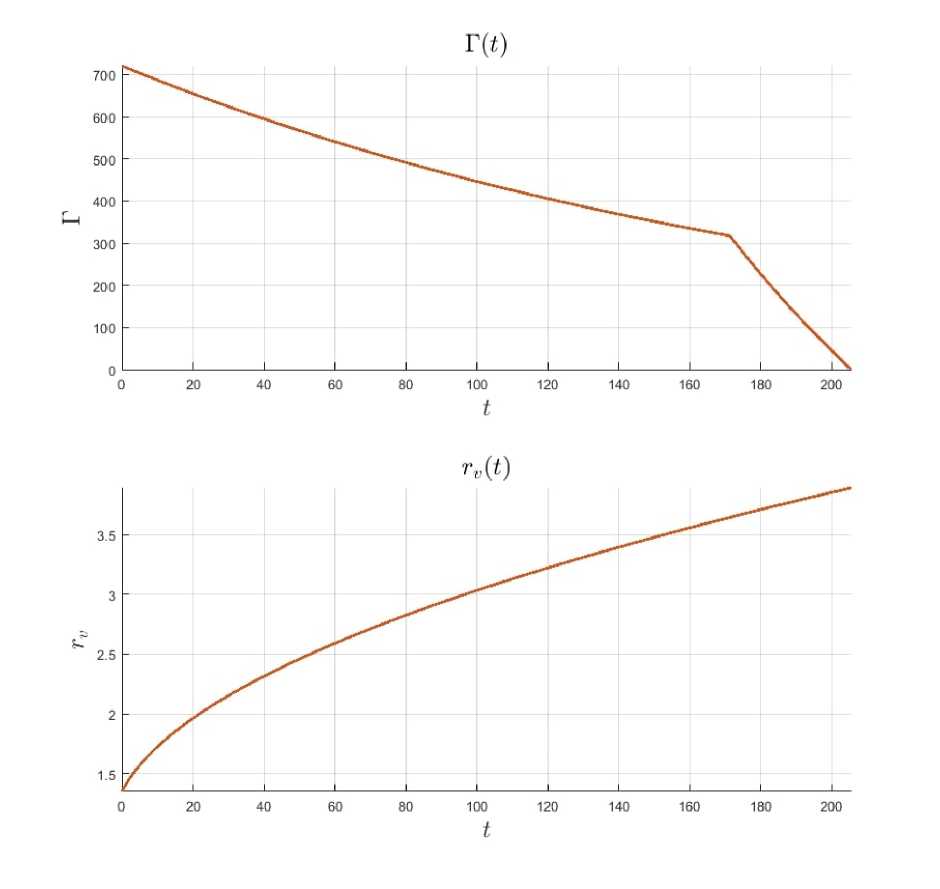
Рис. 2. Зависимость циркуляции Г и радиуса т_у вихревых нитей от времени

Инженерная модель опускания нитей по высоте может быть принята следующей:

dAy     — r(t)b dt     2л(Ь2 + т2)‘

Поле скорости, индуцируемое вихревым жгутом в каждой из контрольных точек, вычисляется посредством разбиения вихря на отрезки.

4.    Модель вычисления дополнительных аэродинамических нагрузок

Дополнительные аэродинамические нагрузки, действующие на самолет, учитываются в модели динамики самолета как линейные добавки к основным нагрузкам путем умножения возмущенных скоростей на матрицы влияния. Для определения дополнительных сил и моментов от вихревых жгутов используется панельный метод. Поверхность самолета разбита на Np ~ 1000 панелей так, что в центре каждой панели находится контрольная точка. Проводится расчет аэродинамических сил и моментов, действующих на самолет в крейсерском полете при единичных возмущениях проекций скорости в каждой контрольной точке и формируются матрицы Ai, A2, A3 размерностей Np х 6 [1]. Введем матрицу компонент скорости, индуцируемой вихревыми жгутами, в каждой из контрольных точек V(Кг), г € [1,Ур]. Тогда коэффициенты аэродинамических сил и моментов вычисляются путем матричного произведения: Расположение контрольных точек панельной конфигурации самолета представлено на рис. 3.

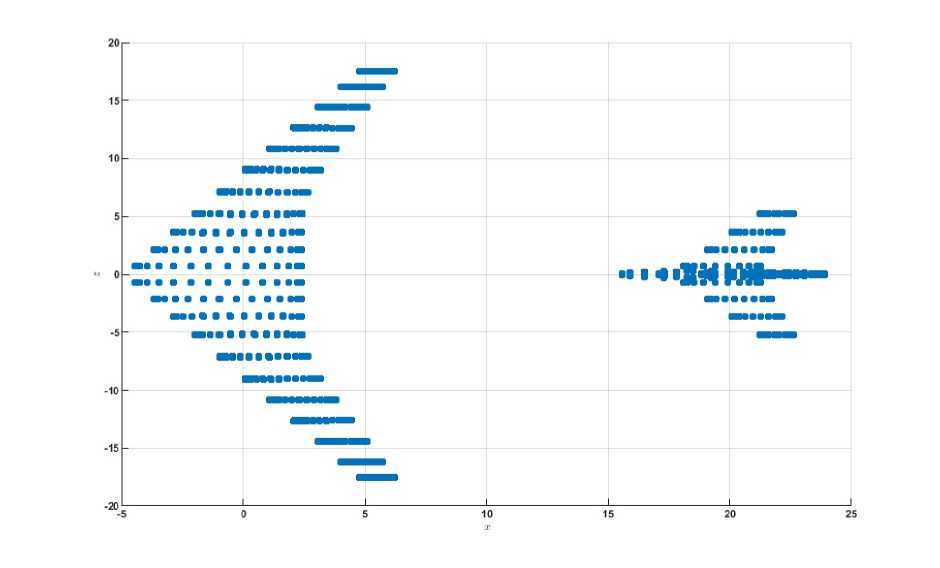
Рис. 3. Контрольные точки панельной конфигурации самолета.

5.    Алгоритмическая реализация модели вихревого следа

Высокое быстродействие описанного метода, обеспечивается двумя факторами:

• •    форма вихревых жгутов может быть посчитана однократно до моделирования на пилотажном стенде (литература, ссылка. [1]);

• •    матрицы A i, A 2, A 3 могут быть посчитаны также однократно до моделирования на пилотажном стенде.

Исходными данными для проведения моделирования являются:

• •    форма правого и левого вихревых жгутов: д,_р(ж),у_пР(ж) и г_л(ж),у_л(ж) в связанной с самолетом-генератором системе координат;

• •    матрицы A i, A 2, A 3:

^

• •    контрольные точки К второго самолета в связанной с ним системе координат;

• •    скорости самолетов, параметры атмосферы, высота полета и начальное угловое положение второго самолета, в земной системе координат.

Одна итерация моделирования полета самолета в вихревом следе состоит из выполнения следующих операций:

• 1.    Перевод контрольных точек из связанной системы координат в земную.

• 2.    Разбиение вихревых нитей на вихревые отрезки и расчет параметров вихревого следа.

• 3.    Вычисление матриц скосов от вихревых нитей во всех контрольных точках.

• 4.    Перевод векторов индуцированных скоростей из земной системы координат в связанную со вторым самолетом систему координат.

• 5.    Вычисление дополнительных аэродинамических сил, моментов и отсылка их в модель динамики самолета.

• 6.    Получение из модели динамики самолета новых значений координат самолета г_с, $,^Щ и его скорости V2.

• 2.    Разбиение вихревых нитей на. отрезки.

6.    Возможности повышения производительности программного компонента

Структурная схема алгоритма приведена на рис. 4.

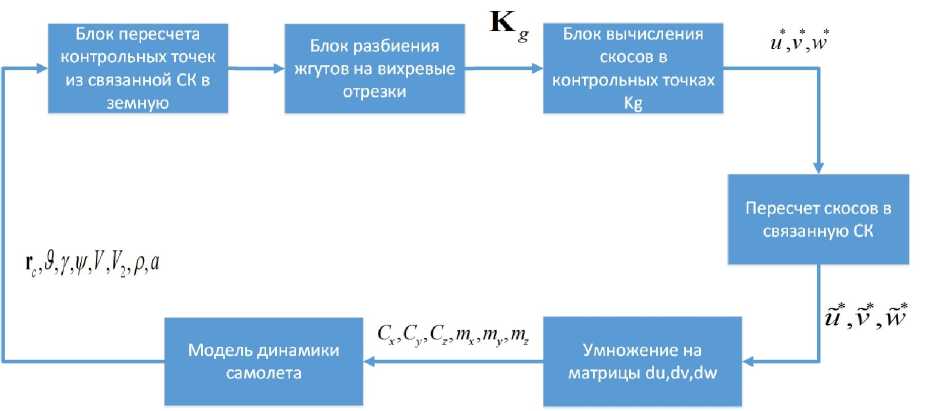
Рис. 4. Структурная схема, алгоритма.

Разберем более подробно отдельные операции алгоритма:

Разбиение производится со сгущением вблизи центра, второго самолета, так как влияние вихревых отрезков убывает с ростом расстояния до точки вычисления скорости. Ввиду ограничения на время выполнения программы количество вихревых отрезков приходится ограничить в ущерб точности. В качестве максимально допустимого размера вихревого отрезка был принят d min = 0.56.

Одним из определяющих требований к реализации математической модели является быстродействие, необходимое для проведения моделирования в режиме реального времени на пилотажном стенде. А именно, время моделирования одной итерации расчета tan должно составлять не более 0.02 с. Указанное быстродействие должно достигаться без ущерба, точности моделирования, которое зависит от количества, участвующих в разбиении вихревых отрезков Щ. Несмотря на быстродействие выбранного метода вычисления дополнительных аэродинамических нагрузок, необходимо все же принять дополнительные меры по увеличению быстродействия программы. Были предложены следующие способы повышения быстродействия:

• 1.    Реализация алгоритма на языке С (за исключением модели динамики самолета, которая реализована в Matlab Simulink);

• 2.    Параллельное выполнение ресурсозатратных операций:

  • 2.1.    Матричное умножение при вычислении дополнительных нагрузок;

  • 2.2.    Перевод скосов и контрольных точек из одной системы координат в другую;

  • 2.3.    Вычисление индуцируемых вихревыми нитями скоростей.

7.    Результаты моделирования

N_y подбирается максимально возможпым. удовлетворяющим требовашпо т <  0.02 с (как правило, N_y ~ 50).

На основе приведенного выше алгоритма был разработан программный компонент на языке С, выполняющий расчет дополнительных аэродинамических нагрузок при попадании самолета в спутную турбулентность. Был проведен ряд расчетов для типовых случаев попадания самолета в спутный след. На рис. 5 приведен случай встречного движения самолета и самолета-генератора под углом курса в 10°.

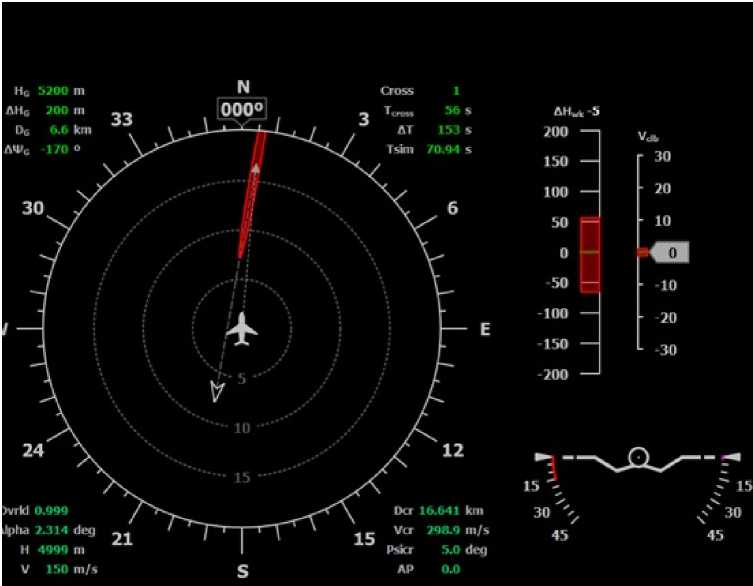
Рис. 5. Встречный курс под 10°

На рис. 6 приведены результаты расчета дополнительных аэродинамических нагрузок, возникших при попадании самолета в спутный след. Попадание в след было произведено приблизительно на 100 с от начала моделирования.

Для данного случая использовался следующий режим: высота 5 км, скорость 150 м/с, самолет-генератор следа - типа А380. Второй самолет - типа МС-21, скорость 150 м/с. Попадание самолета в след происходит на расстоянии 15 км за А380.

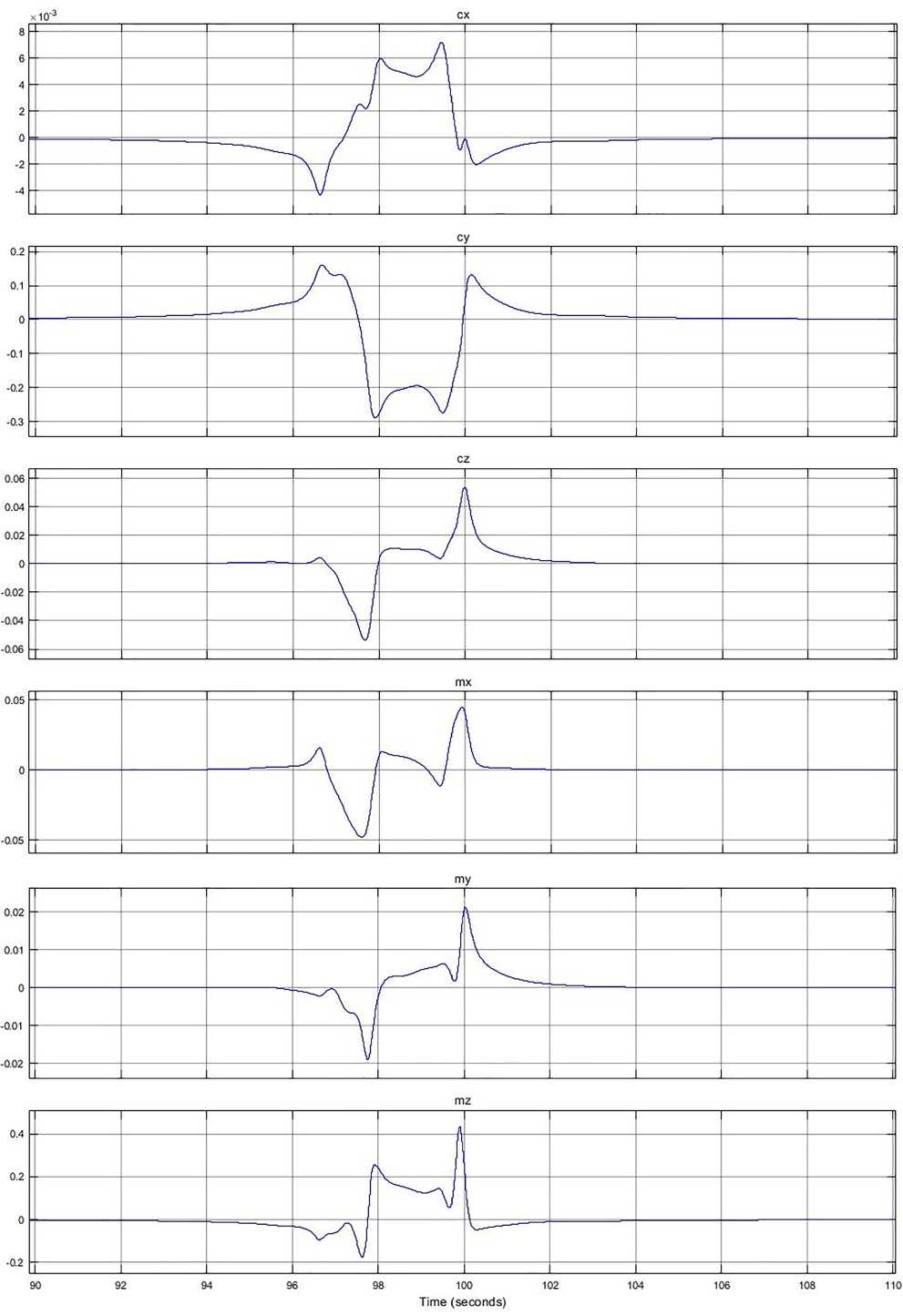
Рис. 6. Результаты расчета дополнительных аэродинамических нагрузок

8.    Благодарности

Данная работа выполнена в рамках Соглашения о предоставлении гранта в форме субсидии от 2019 г. № 05.628.21.0013, заключённому между Министерством науки и высшего образования РФ и ФГУП «ЦАРИ» на выполнение работы по теме «Полунатурное моделирование критических режимов полета пассажирского самолета и рисков, обусловленных человеческим фактором», шифр «SAFEMODE».