Моделирование поля постоянного магнита
Автор: Булыжв Е.М., Меньшов Е.Н., Джавахия Г.А.
Журнал: Известия Самарского научного центра Российской академии наук @izvestiya-ssc
Рубрика: Физика и электроника
Статья в выпуске: 4-1 т.13, 2011 года.
Бесплатный доступ
Предложена математическая модель распределения скалярного магнитного потенциала, создаваемого в окружающем пространстве цилиндрическим или кольцевым постоянным магнитом.
Магнитный сепаратор, эквивалентный соленоид, намагниченность, скалярный магнитный потенциал, напряженность магнитного поля, телесный угол, распределение поля
Короткий адрес: https://sciup.org/148200081
IDR: 148200081 | УДК: 621.31
Текст научной статьи Моделирование поля постоянного магнита
В общем случае для материала магнетика намагниченность М сильно зависит от напряженности поля размагничивании Н = – НР . Однако для магнитных закритических материалов М(Н) выражается формулой
M ( H ) = —B F ( H cb + H ) - H , (2)
^ 0HCB которая описывает слабую зависимость М от Н [2]. В частности, для Nd-Fe-B – материала при изменении Н от Н = 0 до Н = – НСВ относительное различие М (Н) составляет небольшую величину
M ( hcb ) _ ^ 0 hcb
M r Br
< 1,2,
где Mr = М(0). По этой причине значение остаточной намагниченности Мр , определяемое пересечением характеристики размагничивания материала с характеристикой формы, практически не зависит от формы магнита. Однако, тело магнита произвольной формы намагничивается неравномерно [5], за исключением сфероидальной формы. Но в силу слабого характера зависимости М от поля размагничивания (Н = – НР) для магнитов из закритических материалов, этой неоднородностью можно пренебречь и для расчетов можно использовать приближенное значение М ^M r .
На основе закона Био-Савара в [6] проведен расчет напряженности поля соленоида (его аксиальной HZ и радиальной Hr составляющих). Однако, в данной методике содержится дефект, суть которого состоит в том, что напряженность поля как для одиночного контура, определенная в [3,5] через векторный потенциал, так и для однослойной обмотки, определяемая в [6], выражаются через эллиптические интегралы 1-го и 3-го рода. По этой причине данная методика приводит к сингулярности – значения поля в некоторых особенных точках, лежащих на поверхнос- ти соленоида, расходятся. В [7] показано, особенные точки появляются как следствие принятых математических допущений о бесконечно малой толщине токового слоя. А так как потенциал является своего рода первообразной функцией для напряженности поля, то в нем сингулярности могут пропадать.
В [6] приводится, также, строгий расчет напряженности поля постоянного магнита в произвольной точке (как внутри магнита, так и вне магнита). При этом постоянный магнит цилиндрической или кольцевой формы моделируется разноименными фиктивными магнитными зарядами, сосредоточенными на его противоположных торцевых поверхностях. Поверхностная плотность заряда равна sм = ± Mr . Полученные математические выражения поля свободны от дефектов сингулярности, но более сложны, так как представляют собой двойные интегралы.
Нами предлагается строгая и несложная математическая модель скалярного магнитного потенциала цилиндрического магнита диаметром 2a , длиной l .
В [4-5] изложена методика, выражающая скалярный магнитный потенциал jМ, создаваемый контуром с током I, через телесный угол W, под которым виден этот контур где dSсф – площадь элемента сферы радиуса R. Из рис. 1, б следует то, что dSсф = dSКcosO R=(z'2 + r'2 )1/2; cosO = z'/R. (8)
Подставляя (8) в (6) и далее в (7), имеем
Д(А _ z' r'dr'dф d Q —
(z -2 + r '2) 2
Полный телесный угол будет выражаться двукратным интегралом
_ rr z1 r'dr'd ф
Q JJ
S. (z - 2 + r. 2) 3(10)
Вычисление интеграла (10) проводим по методике [7]. На рис. 2 представлена геометрия границ областей интегрирования телесного угла для двух случаев, когда проекция 0' начала координат 0 на плоскость контура лежит вне контура ( rі a ) или внутри контура ( rЈ a ) .
Для случая, когда rі a (рис. 2, а)
У rD мак в
Q — z' J d y J
^
мин
r H
r ' d r '
( z + r ' 2)3
Ф m — 4^ + C , (3)
где С – постоянная величина, так как потенциал определен с точностью до постоянной величины.
Представляя магнит в виде эквивалентного соленоида, предварительно разбивая его на элементарные контура и выделяя некоторый элементарный контур с элементарным током
^
мак
— 2 z * J
2 + Г н
■ 2
+ Г в
(11) d y .
Для случая, когда rЈ a (рис.2,б)
2 n r B 'j ' K
Q — z 'J d ф J — r Г3 — 2 n- 2z 'J 0 0 ( z' 2 + r 2 ) 2 0
J z 2 + Г в в
d VX12)
dI — iW dz ' — M r dz' ,
запишем формулу потенциала элементарного контура dф M = — Mrdz 'Q( z'). 4 n
Сначала определяем телесный угол, под которым виден элементарный контур из точки Р, совмещенной с началом координат (рис.1, а), предварительно разбивая его на элементарные телесные углы dW, под которыми видны элементы площади dSК контура. В полярной системе координат величина dSК = r dTdr’. (6)
Каждый элементарный телесный угол определяется формулой [8]
d q— dS cS- , R 2
Здесь: rн = rн(Y) и rв = rв(Y) радиус-векторы точек входа внутрь контура и выхода из контура луча y = const. Эти радиус-векторы определяются из уравнения окружности, которое в полярных координатах принимает вид r' 2–2r r'cosY+ r2– a2=0, из которого следует:
rв = r cosT+( a2- r2sin2T)12, rн= r cosT-( a2- r2sin2T)1/2; (13)
sin Y = a/r. (14)
мак
Магнитный потенциал эквивалентного соленоида длиной l в точке Р с координатами z и r (рис. 3) складывается из потенциалов (5) элементарных контуров l+zi l+zi фM — JdфM + C — -r- JQ(z'-z)dz' + C.(15) zi 4 П zi
Для случая, когда rі a, подставляя (11) в (15) и меняя местами порядок интегрирования
Ф м
Л f ^ мак 1 + z i
= Mi d ^
2п J J
1 z
^^^^^^^
z
z 1
_ ^ z '2 + Г н2
^^^^^^^
z -
z
z '2+^2
dz ' + C =
дим к классической формуле напряженности осевого магнитного поля [2-3] катушки
!,f ^ Мак Г /----------------------------- I----------------------------
2 _ J [ 7( 1 + z 1 - z )2 + rM - 7( 1 + z 1 - z )2 + r B D + (16)
iW
1 HzV "2T
l
- z
( 2 - z ) 2 + a2
+
2 + z
+7 ( z i - z ) 2 + r e2 - 7 ( z i - z ) 2 + r i2 "I d ^ + C •
Здесь z1 – координата нижней торцевой поверхности магнита, С – постоянная величина.
Для случая, когда rЈ a, подставляя (11) в (15) и меняя местами порядок интегрирования
Ml ф м = —
n 1 + z i
- M7 J d^ J
2 n 0 z 1
z' - z
z2 + r e 2
dz' + C =
M r 1 - M^ J[ <1 2 2 П 0 L
+ z i - z ) 2 + Г в2 -7 ( z i - z ) 2 + r e2 d ^+ C.
Определим осевую напряженность магнитного поля соленоида на основе выражения (17):
Hz = –
5ф м ( r = 0 ) 5 z
M r n 1 + z i - z z i - z
2 n 0 [ 7 ( 1 + z i - z )2 + r e2 7 ( z i - z ) 2 + r e2
d r= (18)
-
M r
1 + zi — z zi — z
-
( 1 + z i — z ) + a ( z ^ — z ) + a
Поместив начало координат в середине соленоида ( z1 = – l /2) и подставляя (1) в (18), прихо-
Такой результат свидетельствует о правомерности полученной модели поля.
Семейство зависимостей для соленоида с геометрическими размерами a = l = 10 м, характеризующее распределение магнитного потенциала в аксиальном направлении по формулам (16)(17) на разных расстояниях rk от оси симметрии, представлено на рис. 4; постоянная С = 0 . На графике пунктирным линиям соответствуют двум распределениям магнитного потенциала на поверхности соленоида ( r = а ). В частности, зависимость 124 соответствует пути интегрирования примыкающего к поверхности внутри соленоида; зависимость 135 – примыкающего к поверхности вне соленоида. Различие этих двух зависимостей обусловлено тем, что путь интегрирования 124 пересекает контур с током величиной Mr(z+l/2) , что приводит к отличию потенциалов в каждой текущей точке на величину частичной МДС F(z) = Mr(z+l/2) . За пределами обмотки (в точках z і10) рассматриваемые зависимости описываются соответствующими участками 46 и 57, потенциалы, в каждой точке которых отстоят друг от друга на одинаковую величину, равную полной МДС соленоида F = Mrl . Такой характер зависимостей магнитного потенциала может приниматься во внимание при разработке магнитной схемы замещения постоянного магнита.
Таким образом, получена математическая
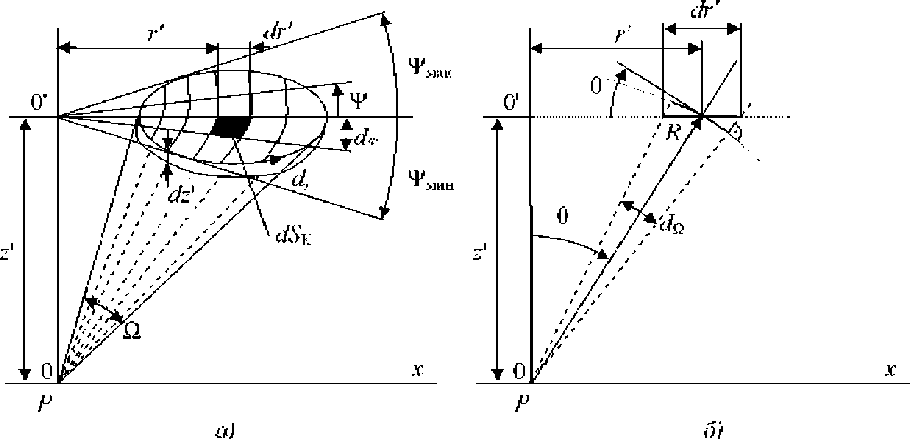
Рис. 1. К расчету телесного угла: а – под которым виден контур с элементом тока di ; б – под которым виден элемент площади dS К контура
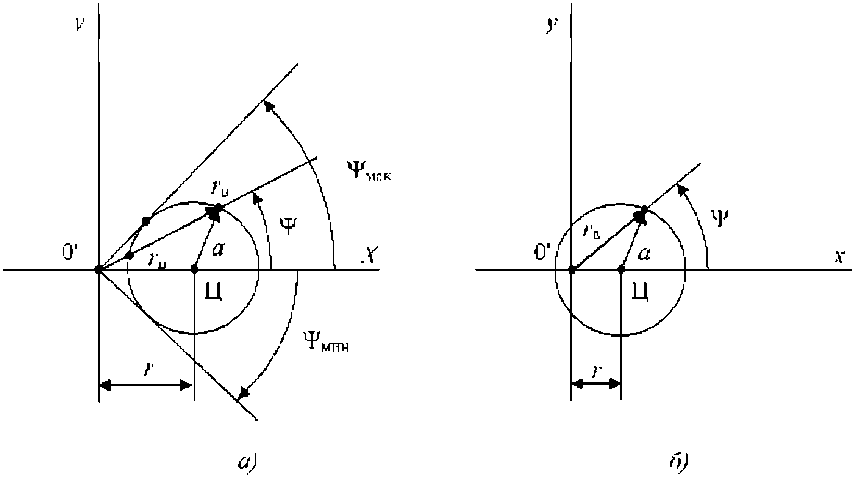
Рис. 2. К расчету границ областей интегрирования телесного угла:
а – для случая, когда проекция 0' точки наблюдения Р на плоскость контура лежит вне контура; б – для случая, когда проекция 0' точки наблюдения Р на плоскость контура лежит внутри контура
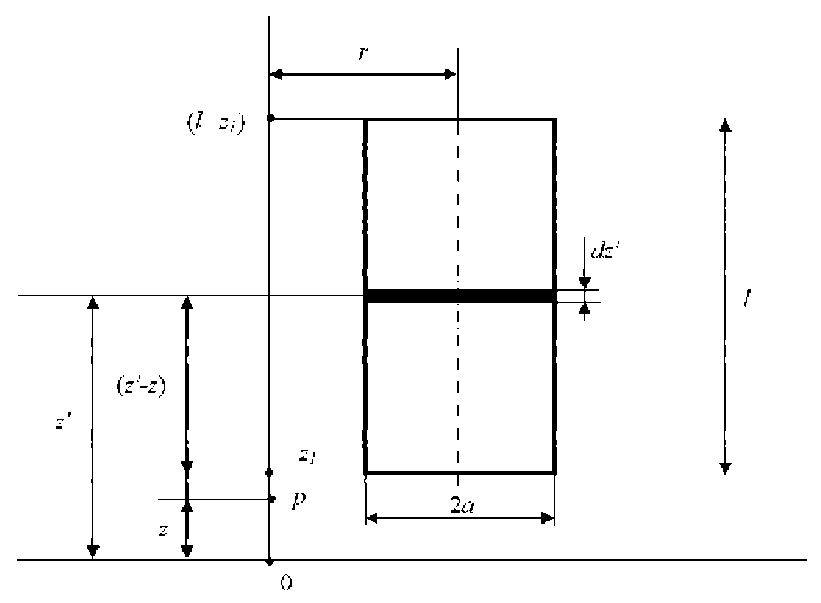
Рис. 3. К расчету скалярного магнитного потенциала эквивалентного соленоида
модель для скалярного магнитного потенциала цилиндрического магнита, состоящая из двух выражений (16)-(17), описывающих распределение потенциала в произвольной точке внешней области магнита. При этом расчет в общем случае сводится к задаче интегрирования по одной переменной и не представляет серьезных трудностей. Данная модель содержит в себе в явной форме параметры постоянного магнита, удобной для анализа поля и может быть положена для анализа внешнего поля магнитов в однородной среде.
Расчет скалярного магнитного потенциала кольцевого магнита проводится тоже по выражениям (16)-(17). Только в этом случае нужно использовать принцип наложения, для определения результирующего поля двух эквивалентных соленоидов с равными, но с противоположными направлениями токов [2].
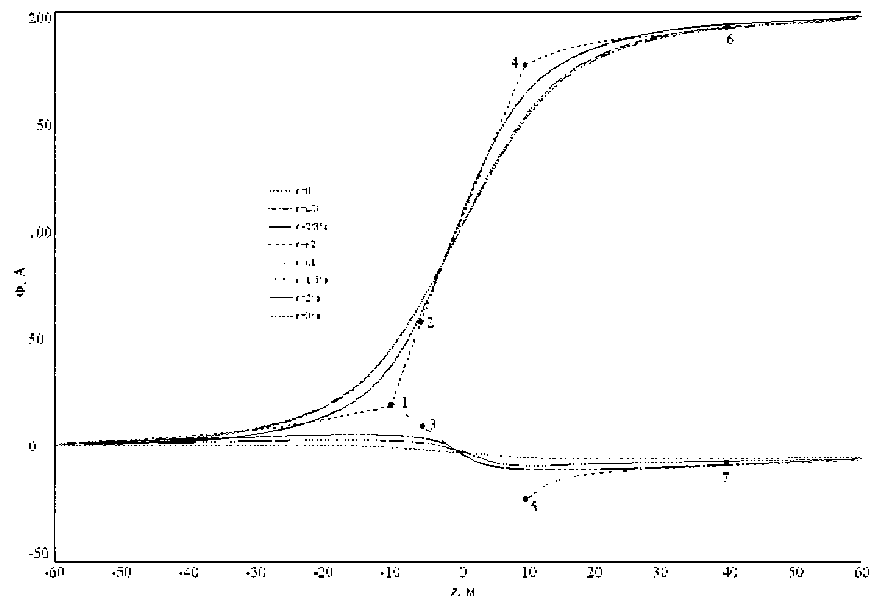
Рис. 4. Семейство зависимостей распределения скалярного магнитного потенциала
эквивалентного соленоида
Исследования выполнены при финансовой поддержке Министерства образования и науки РФ по аналитической ведомственной целевой программе «Развитие научного потенциала высшей школы (2009 – 2010 годы)» на 2009 год, регистрационный номер 2.1.2/4506.
Список литературы Моделирование поля постоянного магнита
- Булыжев Е.М., Худобин Л.В. Ресурсосберегающее применение смазочно охлаждающих жидкостей при металлообработке. М.: Машиностроение, 2004.352 с.
- Постоянные магниты: Справочник/Альтман А.Б., Герберг А.Н., Гладышев П.А. и др.; Под ред. Ю.М. Пятина. М.: Энергия, 1980.-488 с.
- Бессонов Л.А. Теоретические основы электротехники: Электромагнитное поле. М: Высш. школа, 1978. 231 с.
- Тамм И.Е. Основы теории электричества. М.: Наука, 1976.-616 с.
- Нейман Л.Р., Димирчян К.С. Теоретические основы электротехники. Л: Энергоиздат, 1981. Том 2. 415 с.
- Расчет электрических цепей и электромагнитных полей на ЭВМ/М.Г Александрова, А.Н. Белянина, В. Брюкер и др.: Под. ред. Л.В. Данилова и Е.С. Филиппова. М.: Радио и связь, 1983.-344 с.
- Сечнев А.Я. Расчет напряженности поля прямым методом. Л.: Энергоатомиздат, 1984. 112 с.
- Смирнов В.И. Курс высшей математики. М.: Наука, 1967. Том 2. 655 с


