Моделирование порогового эффекта в эффективности воспроизводства волжской популяции осетра

М етоды математического моделирования популяционных процессов развиваются с 20-х годов прошлого века и при существенном интересе исследователей к данной области накоплен набор общедоступных подходов. Можно выделить в классификации большие группы «вольтерров-ских» моделей, формализующих взаимодействие конкурирующих популяций на основе систем ОДУ, методы трофо-динамического подхода предназначены для описания переноса энергии по пищевым цепям. В ихтиологии и энтомологии развивались модели, ориентированные на определение механизмов саморегуляции численности при ограничивающем влиянии выделенных факторов среды. При наличии арсенала моделей практическая организация рационального использования биоресурсов на основе прогностической математического аппарата оценивается как сложная. Поставивший под угрозу исчезновения перелов осетровых рыб Каспийского моря можно объяснить ошибками и развалом системы регулирования эксплуатации, но коллапс рыбных запасов отмечался в странах экологически ответвленным обществом и действующей научно-обоснованной системой регулирования промысла, как в Норвегии [1]. Вынужденными решениями об остановке уже и так оскудевшего промысла удается лишь более или менее своевременно предотвращать дальнейшие необратимые последствия деградации биоресурсов.

К причинам отсутствия универсальной отработанной методики можно отнести то, что построение математического аппарата моделей изначально было слабо связано с данными наблюдений. Теоретическая экология формулируется на уровне качественных принципов, а не строгих законов. Заимствованные из механики методы описания процессов в отсутствии строго формализованных законов оказались не столь эффективны в новой области применения. Начиная с уравнения П. Ферхюльста предполагалось, что популяция характеризуется некоторым репродуктивным потенциалом, r- параметром, что выразилось в том числе в представлении о K- и r- стратегиях выживания видов. Однако, наблюдения свидетельствуют, что r- параметр постоянен только в некоторых усредненных условиях [2].

В статье на основе анализа наблюдаемых эффектов предлагается модель формирования поколений, описывающая скорость убыли численности в раннем онтогенезе рыб. Рассматриваются свойства новой дискретно-непрерывно мульти-стабильной динамической системы. Кратко обсуждается сложноинтерпретируемая динамика применяемых в промысловых расчетах функциональных итераций с появлением хаотического режима.

ДИНАМИЧЕСКАЯ СЛОЖНОСТЬ МОДЕЛЕЙ ИХТИОЛОГИИ

Службами учета Канады неоднократно отмечался нестабильный характер воспроизводства облавливаемых популяций лососевых рыб, мигрирующих для размножения в реки. Фиксировалось отсутствие пропорциональной зависимости R ≈ kS между нерестовым запасом и сезонным пополнением. Возникла теория о роли различных факторов смертности в зависимости от плотности рыб на нерестилищах [3]. Личиночные стадии крупных осетровых и лососевых протекают при высокой плотности, даже если взрослых рыб не так много. Канадский биолог У.Е. Рикер, рассматривая причины уменьшения пополнения при возрастании нерестового стада, предложил теоретическую концепцию о существовании зависимости запаса и пополнения, и роли её свойств при долговременной эксплуатации [4]. Рикер предложил простую, как казалось, формулу расчета величины пополнения R = f (S):

f (5) = aS exp(-bS \ (1)

где S - от английского «stock» величина нерестового запаса, b - коэффициент, отражающий величину, обратную количеству производителей, при котором число выжившей молоди максимально, имеет смысл b = 1 ; а - параметр характеристики репродуктивного потенциала. График зависимости пополнения от численности производителей называется кривой пополнения. (1) задает куполообразную кривую с асимптотой lim _S ^_v f ( S ) = 0 и единственным нетривиальным пересечением с биссектрисой координатного угла R = S .

Очевидно, что при применении модели (1) возникает ряд сложностей. При увеличении количества отложенной икры выживаемость молоди должна уменьшаться до неразличимых значений, что противоречит наблюдениям над аквариумными популяциями. Пополнение уменьшается до некоторого Q > 0 = const. (1) при моделировании на ЭВМ сообщества гидробионтов часто использовалась как кусочно-гладкая, до некоторого критического количества 5с, при S > 5с количе- ство молоди предикативно устанавливалось

Q = const.

При низких численностях производителей (1) предсказывает увеличение скорости воспроизводства. При стремящемся к нулю количестве отложенной икры, эффективность пополнения стре- мится к предельному значению:

^ = а exp( - bS )(1 - bS ), lim а exp( - bS )(1 - bS ) = а .

(1а)

Подобное свойство сделало сомнительным использование (1) для моделирования деградиро- вавших из-за нерационального промысла популяций рыб, в частности интересующей нас динамики численности волжских осетровых. Более того, (1а) не соответствует концепции экологии, известному как принцип Олли (W. Allee) [1].

Модель (1) обладает интересными свойствами, о которых не имел представления ее разработчик и потому не предложил для них адекватной биологической интерпретации.

Представим процесс изменения состояния популяции, определяемый зависимостью запас-пополнение в виде динамической системы, математического объекта, для которого можно указать набор величин: динамических переменных, ха-растеризующих состояние системы. Значения таких переменных в последующий момент времени рассчитываются из текущих значений по закону, называемому оператором эволюции. Динамическая система представляется тройкой (M , T , у), состоящей из фазового пространства M , времени T , оператора эволюции у. Для V x е M и V t , s е T выполняется      условие:

у(у( x, t), s ) = у ( x, s +1).

Множество {у(‘)(x)}teT фазовая траектория точки x. Графически эволюция диссипативной динамической системы во времени представляется движением точек в фазовом пространстве к аттрактору, подмножеству фазового пространства A c M инвариантное относительно эволюции: у(t) (A) = A для всех t е T и такое, что существует окрестность U множества A, в которой для всех у е U выполняется lim у(1) (у) = A. Регу-t→∞ лярными аттракторами для отображения интервала у : I ^ I считаются состояние равновесия с неподвижной точкой x : lim у( t)(у ) = x и устой-t→∞ чивый цикл, соответствующий режиму периодических автоколебаний.

Стремящиеся к одному аттрактору множество точек есть его область притяжения, которая может быть непрерывным подинтвалом Qc I , так и образовывать фрактальное множество [5]. Рассмотрим динамическую систему как полугруппу итераций { у ⁽ j ) } j _{а 0} , и пусть R o , R 1 , R ₂,... последовательность точек эволюции системы, определённых условием R j _{+ 1} = у ( R j ) при всех j >  0. Качественное поведение зависит от параметра а, он является управляющим. До определённого значения а , не превышающего бифуркационное, система стремится к точечному аттрактору R = ln а/ b . Первый метаморфоз поведения системы происходит, когда производная, вычисленная в неподвижной точке, перестаёт удовлетворять критерию устойчивости |у'( R )| <  1. Для (1) это происходит при выполнении условия 2 а > е.

v'( R ) = a e bR - bRa e ^bR ,

• - ь ln a , ln a - ь ln a a (1 - In a )

• V'( R) = a e ^b - b a e ^b = = 1 - ln a . b e ln a

1    - ln a = -1, a = e2.

Параметр b не влияет на топологические характеристики фазового портрета. Динамическая система стремится в устойчивое циклическое состояние с периодом 2: глобальный аттрактор, состоящий из двух периодических точек. Факт, что x_{n + 1} = ax_n e ^bx n имеет в большом диапазоне параметра цикл, говорит о том, что не стоит от построенного по эмпирическим данным графика ожидать характерной куполообразной кривой.

Далее увеличивая a, будем наблюдать рост амплитуды колебаний, и по достижению порогового значения a> 12.51, произойдёт бифуркация удвоения периода и установится цикл p = 4. При дальнейшем увеличении a все быстрее реализуется каскад бифуркаций удвоения периода. Около a >14,8 невозможно выделить устойчивых точек или замкнутого цикла. Происходит детерминированный хаос, напоминающий стохастический процесс очень чувствительный к начальным условиям. Траектория притягивается к подмножеству фазового пространства, получившему из-за своих фрактальных свойств название «странный аттрактор». Важно знать, что сценарием хаотиза-ции через бесконечный каскад удвоений, иссле-дованым на примере x_{n + 1} =П x_n (1 — x_n ) М. Фэйгенбаумом в [6], спектр нелинейных эффектов не ограничивается. В ограниченных диапазонах при a >14,8 наблюдаются «окна периодичности» устойчивых циклов p * 2 i , далее вновь испытывающих удвоения.

В x_{n + 1} = ax_n e ^bx n наблюдаем последовательность касательных бифуркаций с появлением устойчивых циклов периодов p * 2 i . Ли и Йорк в 1975 г. опубликовали статью «Period three implies chaos», где показали, что если одномерное отображение R j _{+ 1} =v ( R ) при некотором значении параметра a = a имеет цикл периода p = 3, то оно при a ) имеет и бесконечное множество циклов всех других периодов. Ранее А. Шарковский в [7] доказал, если одномерное отображение f : I ^ I имеет цикл p = n , то оно также имеет циклы со всевозможными периодами n % _i , предшествующими числу n , среди целых чисел, выписанных в порядке Шарковского, который завершает число три.

Появлению окон предшествует явление «перемежаемости» (отмечен стрелкой на рис. 1). Перемежаемостью считается режим чередования во времени почти регулярных колебаний (ламинарная фаза) с интервалами хаотического поведения (турбулентная фаза). Перед появлением циклических точек ветви графика третьей итерации функции f 3 (x) образуют так называемые каналы, в строгой последовательности по которым траектория движется довольно долго, что соответствует ламинарной фазе перемежаемости. Выход точки траектории из канала определяет короткую турбулентную фазу – отчетливо видимый на графике «всплеск». Такое поведение может служить индикатором скорых резких изменений.

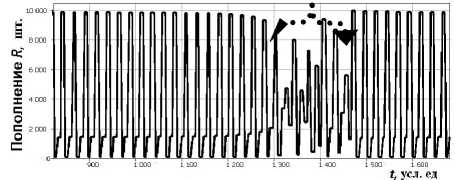
Рис. 1. Перемежаемость с циклом p = 3 в xn+1

= ax„ e ^b x ⁿ

ПРОБЛЕМА ИНТЕРПРЕТАЦИИ НЕЛИНЕЙНОСТИ

Появление хаоса интерпретировалось в биологическом контексте как последствие повышения репродуктивного потенциала популяции. В (1) это a , но для динамики подобных унимодальных отображений при [ a , a ] мы увидим набор резких изменений поведения, для которых нам трудно найти рациональное толкование. При использовании более сложных нелинейных дискретных моделей практические выводы будут определяться свойствами критерия устойчивости аттрактора как функции нескольких переменных. Рассматривая различные воздействия на популяцию, подчиняющуюся (1), мы получим, например, что искусственное воспроизводство хаотизирует динамику, а промысел наоборот уменьшает амплитуду колебаний. Однако, выводы будут универсальны для целого семейства итераций функций, удовлетворяющих критериям теоремы Д. Синджера, называемых SU- отображения.

Для построения куполообразных кривых запас-пополнение были предложены довольно сложные преобразования исходных данных наблюдений. Возникает вопрос: имеют ли смысл методы построения кривой, если эмпирические данные о воспроизводстве не прошедшей все стадии деградации популяций и для которых справедлива (1), будут представлены в виде сгущений точек на графике, а не ожидаемой куполообразной кривой с явным максимумом.

Не для всех рыб актуальна теория пополнения, в гораздо большей степени ее методы обоснованы для анадромных видов, заходящих из морей для нереста на речном грунте.

ПРОБЛЕМА РЕЗКОГО СОКРАЩЕНИЯ ВОСПРОИЗВОДСТВА

Изучение ретроспективных данных о популяциях анадромных рыб Нижней Волги позволило выявить нелинейные особенности в формировании пополнения. Общей задачей наших исследований является анализ на основе вычислительных модельных сценариев антропогенно-обусловленных процессов деградации биоресурсов экосистемы Волго-Каспия. К прогнозированию уловов осетровых методы динамической теории пополнения У. Рикера ранее не применялись, основным фактором считался гидрологический режим реки.

Среди разнообразной опубликованной информации интересны сведения о количестве молоди осетра, полученной от некоторого запаса, обработанные нами методом скользящей средней (рис. 2). Количество пропущенных на нерест в Волгу производителей за период наблюдений изменялась существенно: от 2500 тыс. экз. в 1979-81 гг. до 25 тыс. в 2000-х гг. [8]. В настоящее время мы не имеем достоверной информации о нынешнем состоянии популяции Acipenser gueldenstaedtii и численности нерестовой части. С 2010 г. волжские популяции осетровых внесены в «Красную книгу» и промысел запрещен. Имеющиеся сведения с 1968 г. об общей численности осетровых Каспия по данным тралового учета [9] многими специалистами оцениваются как сомнительные [10] и менее достоверные, чем информация о проходе производителей на нерестилища в створе реки.

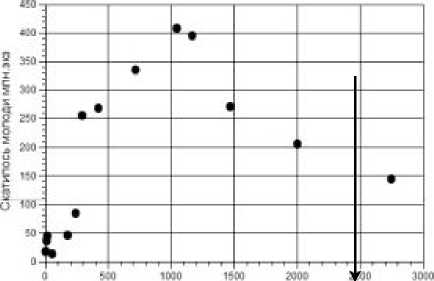
OpcnsmeHO производителей 'осетра" тыс. эко

Рис. 2. Данные о воспроизводстве осетра

Acipenser guldenstaedtii .

Кривая воспроизводства осетра (на рис. 2 среднее по трем ближайшим) характеризуется как изломанная куполообразная. Мы можем восстановить отчетливо гладкую кривую, а не сгущение точек. Следовательно, популяционная динамика определялась промысловой смертностью более, чем зависимостью f (S). Стрелкой отмечен момент: при пропуске менее 350 -103 шт. непропорционально резко уменьшается количество скатывающейся в море молоди. Выявлен статистически достоверный пороговый эффект скачкообразного перехода эффективности воспроизводства на некий отличный от нуля минимальный уровень.

Подобное явление оказалось характерно не только для единственной волжской популяции. Сам У. Рикер не рассматривал (1) как единственно возможную нелинейную форму зависимости между запасом и пополнением, описав в работе [11] неожиданный для промысла эффект резкого падения воспроизводства, нарисовав для его объяснения кривую воспроизводства как подобие ступенчатой функции. Рикер назвал эффект «лезвием ножа», т.к. даже небольшой перелов 5% может подорвать запасы такой популяции и потому оптимальная стратегия промысла, изымающая весь излишний прирост нерестового стада, крайне опасна для практики в плане стабильной долговременной эксплуатации.

Зоологами неоднократно подтверждалось для не заботящихся о потомстве видов , что существует оптимальный для воспроизводства диапазон численности репродуктивной части популяции. При уменьшении численности эффективность воспроизводства рыб должна снижаться, так как уменьшается вероятность встречи особей разного пола, пригодных для размножения участках рек, но ожидаемое снижение может оказаться непредвиденно резким.

Модельное описание амплитуды изменения репродуктивного потенциала, с сохранением гладкого характера зависимости, целесообразно провести с применением современного подхода к вычислительному исследованию гибридных динамических систем.

РАЗРАБОТКА НОВОЙ РЕПРОДУКТИВНОЙМОДЕЛИ

Наличие ограниченных пищевых ресурсов в неявном виде учитывалось известными моделями, но общим недостатком функциональных итераций нужно считать игнорирование проявления декомпенсационного фактора смертности. Не учитывался фактор изменения пищевых потребностей по мере развития молоди, которое происходит синхронно с началом сезонного уменьшения кормовой базы. Декомпенсационные факторы - увеличивающие смертность при уменьшении плотности особей снижают эффективность нереста, уменьшая количество икры реально вступившей в репродуктивный процесс при S = R . Прямой учет такой зависимости становится очевидной необходимостью при моделировании динамики популяций подвергающихся перелову. Задачей разработки новой модели запас- пополнение стало создание гибкого математиче ского аппарата для согласования качественного характера поведения имитационной модели промысловой популяции с ретроспективными данными о численности молоди волжских анадромных рыб в различные годы и объеме вылова.

Очевидно, что поведение модели зависит от математических особенностей выбранной функции воспроизводства, особенно вне диапазона оптимальной численности нерестового стада. Важны не только наличие минимума и максимума зависимости, но и точки перегиба.

Формализуем увеличение пищевых потребностей молоди исходя из факта, что скорость роста находится в обратной зависимости от численности поколения, но не в обратно пропорциональной. Это согласуется с данными наблюдений биологов в частности, с результатами экспериментов над ростом рыб при различной их плотности. Согласно наблюдениям, при увеличении плотности возникает асимметричное распределение размерной структуры популяции в сторону преобладания особей с меньшими размерами. Описывать убыль численности поколения N(t) на интервале модельного времени [0,T] будут следующие объединённые в систему дифференциальные уравнения (а, в, с — константы):

dN = -(a w (t) N (t) + 0( 5 )P) N (t)

dt

<

dw = , = g , w<0) = Wo, N(0) = X5. dt VN (t) +z где: 5 - величина нерестового запаса; w(t) - отражает уровень размерного развития поколения, влияющий на увеличение пищевых потребностей; g - параметр, учитывающий ограниченность количества доступных для молоди кормовых объектов. Z — параметр ограничивающий темп развития вне зависимости от N(t); X -средняя плодовитость особей; а - коэффициент компенсационной смертности; в - коэффициент декомпенсационной смертности; к е (1,2); ин тервал уязвимости t е [0, T] специфичен для ви- да.

У бывающая функция 0 ( 5 ) = 1 + exp( - c5 ²), lim ₅ ,, 0 ( 5 ) ^ 1 отражает действие известного в экологии эффекта Олли (W. Allee) или более точнее «эффекта агрегированной группы». Отмечалось неоднократно, что для животных ведущих стадный образ жизни выживаемость молоди в группе повышается, хотя такое существование увеличивает пищевую конкуренцию у взрослых. Когда численность нерестового стада низка, то большая протяженность русловых нерестилищ становится уже негативным фактором.

Функция эффекта Олли 0 ( 5 ) введена в уравнение для N ( t ) , а не в переопределение начальных условий N (0) = f ( X 5 ) т.к. даже не вступившие в репродуктивный процесс кладки икры после их гибели ухудшает токсикологическую обстановку на нерестилище. c -характеризует степень действия эффекта, который не проявляется если численность взрослой части популяции осетровых достаточно велика. При незначительном количестве повторно нерестующих рыб численно получаем 5 = N(T ).

Графиком исследованной с применением численного решения в инструментальной среде последовательности задачи Коши (2) для вычисления численности выживших особей поколения к моменту времени T новой модели является унимодальная кривая с уменьшающимся наклоном ниспадающей правой ветви. Кривая имеет ненулевую горизонтальную асимптоту, две нетривиальные точки пересечения с биссектрисой координатного угла R=5 и характеризуется при двух точках перегиба незнакопостоянным дифференциальным инвариантом Шварца (рис. 3). Фазовое пространство в случае динамической системы V n ( R 0 ) на основе системы (2) разделяется на две области притяжения: Q 1 и Q ₂ . Границей между ними является неустойчивая стационарная точка R (2¹)ервого пересечения кривой с биссектрисой R = 5 . Второе равновесие R ₂ устойчиво.

Анализ устойчивости неподвижных точек дискретно-непрерывной системы в инструментальной среде можно проводить с использованием свойства второй итерации v ( v ( x )). Необходимым и достаточным условием устойчивости неподвижной точки одномерного отображения x *является неравенство: V ² ( x ) >  x при x < x * , V ² ( x ) <  x при x > x * .

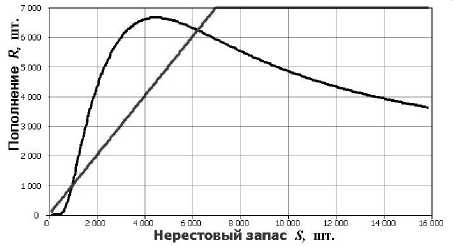
Рис. 3. Зависимость R = f (S) полученная из системы (2).

• ( 2) исследовалась с применением отечественной инструментальной среды моделирования AnyLogic- 6, предоставляющей выбор численных методов с изменяющимся шагом интегрирования

для работы с системами ОДУ первого порядка записанными в форме Коши.

ЗАКЛЮЧЕНИЕ

Поведение траектории динамической системы, с использованием в качестве оператора эволюции решение задачи Коши (2), качественно отличается от итераций (1) возможностью притяжения к двум аттракторам. Соответственно присутствуют две области притяжения, границей которых служит репеллер, неустойчивая особая точка первого пересечения кривой с биссектрисой координатного угла. Траектории с начальными условиями, разделёнными репеллером, покидают его окрестность и приближаются к разным аттракторам. Один из аттракторов точка (0,0) на плоскости R x S . Если численность популяции соответствует области притяжения этого аттрактора, произойдёт вымирание. Данное свойство отражает наличие минимально допустимой численности для существования вида.

Для промысла кривая подобного вида на рис. 3 означает, что популяция долго способна поддерживать высокий процент изъятия, но потом произойдет резкое снижение уловов, которое очень сложно предвидеть экспертам. Деградация может растянуться на длительный период, когда численность популяции будет колебаться около неустойчивого равновесия. В подобной ситуации главное вовремя оценить, что действительно происходит с запасами и своевременно ввести мораторий на промысел, не уповая на хороший уровень половодья.

Работа выполнена при поддержке РФФИ (Проект 13-07-00925).