Моделирование потерь в электроэнергетических системах с использованием аппарата Грама-Шмидта и коэффициентов распределения

Для электроэнергетики России одной из первостепенных задач является задача снижения технологических потерь электрической энергии, которые составляют до 10–15 %. В наметившихся условиях интеграционных процессов и возрастающих интересов к интеллектуальным технологиям возникают требования к развитию более совершенных методов управления режимами электроэнергетических систем и поиску эффективных подходов, алгоритмов для решения задачи определения потерь мощности или энергии.

Актуальность

В теории управления электроэнергетическими системами до настоящего времени разработанные методы, алгоритмы в основном связаны с задачей анализа, определения потерь мощности [1–4]. Но в условиях разнородности нагрузок узлов электрических сетей существующие методы не обеспечивают получения точных результатов [5]. Поэтому для решения подобной задачи необходимо продолжить исследования и ожидать появления новых математических моделей и алгоритмов на базе определения потерь электрической энергии.

Постановка задачи

Исходя из указанного состояния задачи, при развитии новых отношений между производством, транспортом и потребителями электроэнергии предлагается рассматривать определение потерь как распределение потоков энергии в схеме электрической системы за некоторый интервал времени, нежели рассматривать данную задачу в среде распределения потоков мощности на основе узловых матриц Y или Z [6, 7], как это наблюдается в отечественной и зарубежной практике.

Методика определения потерь электроэнергии

Для разработки задачи предлагается представить режимные параметры электрических сетей в виде нагрузок узлов i, моделируемых вектором графиков полных мощностей s (t ) = [ si (t) ] = [Pi( t) + jqi(.t)], * = 1, n , (1)

где Pi(t ) = Pifip (t), q(t) = Qtf4 (t) - соотаетст-венно функции времени активных и реактивных мощностей; pi,qi – соответствующих средних величин; fp (t), f? (t), - базовых функций узло- вых нагрузок, нормированных по средним значениям

TT

P i ( t ) = t J P i ( t ) ^d t , t f ff ( t ) ^d t = 1;

T0             T0                    (2)

qt( t )=| J q( t)d t, | J fq(t) dt = 1;

T0         T0

n– число независимых узлов сети.

Величины p_i как интегральные характеристики для реализации моделей узловых нагрузок (1) рекомендуется определять, используя показания счетчиков энергии или по зарегистрированным данным диспетчерской ведомости, хранящимся в базах данных оперативноинформационных комплексов энергообъектов. Функции f^p ( t ) наиболее целесообразно моделировать типовыми (отраслевыми) графиками активных мощностей, функции же f iq ( t ) можно воспроизводить по графикам f^p ( t ) с учетом изменения значений коэффициентов мощности в узлах сети.

Для получения более универсальной узловой модели определения потерь электроэнергии предложено рассматривать физические процессы в сетях в пространстве ортогонального базиса к исходному. Последний образуют s i ( t ) как линейно независимые функции. Набор некоторых функций h i^p ( t ) образует ортогональный базис. Исходный неортогональный базис преобразуется в ортогональный с применением процесса ортогонализации Грама-Шмидта [8].

В данном процессе каждая последующая координатная ось, получаемая при помощи выражения i-1

h ip ( t ) = ( tУТ?" ( tY (3) j = 1

формируется как ортогональная ко всем предыдущим уже ортогональным осям hip (t). Значения неопределённых множителей X' определяются из следующего равенства

TT

J hp (t) hj (t )-J f' (t yj (t) dt -00

T

-X j J hj (t) hj (t )dt - 0, как

TT

Xj-J fp (t )h' (t) dt  J hj (t) hj (t )dt.

В качестве первой координаты ортогонального базиса может быть выбрана любая функция из набора fip (t) , например, f1p (t) . Для преобразо- вания ортогональных

функций hi p ( t )

в орто-

нормированные следует каждую из них разделить на ее норму vj (t)- hip dt . (5)

На основании выражения (5) математические вектора-функции

операции

определения

F' (t)=[ fi' (t)] сводятся к следующим матрич- ным операциям от времени t

0 ... 0

^F ' ( t ) -

^X '

...

X

......

p

^X n1

p

^X n 2 ... ¹

X

h 2 ^p

Vp (t)- hnp

-Л ^p H ^p V ^p ( t ) ,                    (6)

где Лp -нижняя треугольная с единицами на глав- ной диагонали матрица множителей Xp (3); Hp -диагональная матрица норм ||hp|| функций hip (t),

T ²

I h d -j ( h p ( t ) ) d t .

Вектор-функция полных нагрузок (1) узлов с учетом выражения (6) принимает вид

s (t ) = p (t) + jq (t )-

- р Л ^p H ^p V ^p ( t ) + j q Л q H q V q ( t ) .     (8)

Связь вектора напряжений с нагрузками узлов обеспечивается на основе уравнений в форме баланса мощностей в окрестности средних значений узловых напряжений на отрезке времени Т и с использованием формулы (8) представляется следующей матричной записью

U ( t ) - J ( р Л ^p H ^p V ^p ( t ) - j q Л q H q V q ( t ) ) , (9) где J – матрица Якоби, элементы которой вычисляются в указанной окрестности узловых напряжений схемы электрической сети.

Потери электрической энергии в элементах сети, среднечасовое значение на фазу которых за период [ 0,T ] на основе выражения связи (9), определяются

T

А Э - - JU T ( t ) GU ( t ) d t -

^T 0

1 T           *           nn

- ^- J s T ( t ) Bs ( t ) d t - £ B j + £ B q , (10)

T 0                            i-1

где [ B ii ]- B ^p - H ^p ( Л ^p ) T p ( J ) ^T G J ^‘р Л ^p H ^p , [ B iq ] - B ^q - H ^q ( л ^q ) ^T q ( J ) ^T • G J ^-1д Л ^q H ^q -квадратные обобщенные матрицы коэффициентов B _i ^p _i , B _i ^q _i формул потерь, G – квадратная матрица

Электроэнергетика

узловых проводимостей ветвей сети; Т – признак транспонирования.

Потери электроэнергии при задании режимных параметров комплексными токами в узлах нагрузок j(t)= j'( t)+ j j"(t) за расчетный период вре- мени Т моделируются выражением

А Э = Re

T

= J j ⁷ (t) Zj (t)d t

T 0

= ^{1 7} K ^j '( t ) B ^j к ^j ' ( t ) d t +

T 0

T

+ - J K ^j ( t ) B ^j K ^j ( t ) d t =

T 0

nn T

= S S Bl - J kj (t) kj (t )d t + i = 11 = 1     7 0

nn T

+ S S Bl - J k{ ( t ) k{ ( t ) d t = i = 1 1 = 1      ⁷ 0

nn

= Z Bj + s Bj , i = 1 i = 1

где

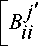
Bj ii

= b ^j' = h ^j' ( л ^j' )7 j ' ^T Rj ’ A ^j' H ^j' ,

= Bj" = Hj" (лj" )T j"TR j"лj"Hj'' - квадратные матрицы формул потерь.

На основе другой модели

■ f(t ) ] = J ( t ) = [ JMt ) ] ^,

которая представляет вектор-функцию узловых токов, рассмотренных через средние значения модулей токов Ji за период Т и функций времени ft (t), среднее значение каждой из которых на интервале времени (0,Т) равно единице, также предложен метод определения потерь электроэнергии. Значения режимных параметров Ji определяются по потреблению электроэнергии в узлах сети. В зависимости от условий задачи потери могут определяться при номинальных, средних значениях напряжений или диспетчерских данных для соответствующих суток. Функции fi (t) воспроизводятся по графикам fp (t) с учетом изменения значений коэффициентов мощности в узлах сети (возможно использовать средневзвешенные коэффициенты или коэффициенты в соответствии с расчетом пото-кораспределения мощностей в нормальном режиме, режимах для характерных суток).

Токораспределение в ветвях сети с использованием узловых нагрузок(14) определяется формулой

I ( t ) = CJ ( t ) , (15)

где C = |_Су ] - обобщенная матрица коэффициен- тов распределения узловых токов по ветвям схемы питающей сети.

Для данной модели в качестве базиса исходного пространства рассматриваются линейно независимые функции f ( t ) . Пусть ряд некоторых других функций, допустим h . ( t ) , образуют ортогональный базис. Используя преобразования аналогичные (3)-(6), вектор-функция [ f ( t ) ] = F ( t )

запишется в виде
F ( t ) =	■ 1      0    ... 0 " 1 21     1    ... 0 ......	П h ,|   0 ...   0 " 0   I h 21 ...   0 K ( t ) = ......
В	_1 „ 1 1 n 2 ... 1 . = A HK ( t ) . формуле	_ 0      0 ... hhn\ 1. (16) (16)     вектор-функция

K (t) = [ki (t)] - обозначает набор ортонормиро- ванных функций ki (t).

С использованием формулы (16) выражение (15) позволяет получить вектор токораспределения для схемы электрической сети в следующей матричной форме

I ( t ) = CJ A HK ( t ) .            (17)

Потери электроэнергии в питающей сети за период T определяются выражением

TT

А Э = 1 J I ^T ( t ) R b I ( t ) d t = 1 J K ^T ( t ) B J K ( t ) d t =

T0T nn    T

=SS BJ 7 Jki (t)k, (t) dt=S BJ.(18)

i=1 j=1      T 0

Здесь RB – диагональная матрица активных сопротивлений ветвей схемы сети; BJ – квадратная обобщенная матрица коэффициентов Bij фор- мулы потерь,

B ^J = H ( A ) ^T JRJ A H , (19) R – обобщенная матрица узловых сопротивлений сети, R = C ^T R B C .

Потери электроэнергии Э определяются суммой диагональных элементов матрицы B ^J , поскольку скалярные произведения ортонормиро-ванных функций k i ( t ) равны [8]. Данный подход можно использовать для оценки распределения потерь электроэнергии в схемах электрических сетей, а не мощностей, которые учитываются при решении многих задач и описаны в разных литературных источниках [9, 10].

Экспериментальные исследования

Модель определения потерь электроэнергии с ортогонализацией базиса задачи была апробирована на примере схемы экспериментальной электрической сети со следующими исходными данными: 0 – балансирующий узел; режимные параметры (токовые нагрузки) имеют следующие характеристики:

0,5

первый узел - J 1 ( t ) = J 1 f 1 ( t ) = 10 1,0

,A;

0,5

0,3

второй узел - J 2 ( t ) = J ₂ f 2 ( t ) = 20

0,8 ,A;

0,5

0,2

третий узел - J 3 ( t ) = J 3 f 3 ( t ) = 20

1,0 ,A;

0,5

схемные параметры(величины сопротивлений ветвей и их топологические связи): R ₀₁ = 4 Ом, R ₁₂ = 2 Ом, R ₁₃ = 3 Ом.

Ортогональный план (базис) для данной задачи определяется функциями времени h 1 ( t ) , h 2 ( t ) и h 3 ( t ) .

Не останавливаясь на подробностях промежуточных действий, мы получаем результат с использованием обобщенной матрицы коэффициентов формулы потерь (19)

B J = Н Л T JRJ Л H = ... =

68046,9 8255, 2 2840, 0

8251,6 1020,0 363, 6

2838,5 362,3  168,0

Матрица BJ имеет размеры, определяемые числом узлов(независимых) схемы электрической сети. Следовательно, результаты расчетов потерь в этом случае носят узловой характер, полученный с помощью матричного аппарата.

В работе [10] приводится описание определения и процесса расчета потерь мощности в схеме электрической сети на базе матрицы Z . Представленный процесс назван «матричным распределением потерь мощности в электрических сетях», что скорее всего будет обозначать определение потерь мощности на базе узлового метода с использованием обобщенной матрицы узловых сопротивлений Z .

Небольшая асимметрия значений элементов (20) получилась за счёт округлений до второго знака после запятой норм h ₁ и h ₃ диагональной матрицы H . Потери электроэнергии в схеме сети вычисляются как 3

АЭ = T B ii = ( 68046,9 +1020,0 +168,0 ) = i = 1

= 69,2кВт/ч.                         (21)

При значимых нагрузках узлов сетей метод определения потерь электроэнергии с ортогонализацией базиса задачи является точным и не имеет методической погрешности, что подтвердилось расчетом суммирования потерь на часовых ступенях графиков токов ветвей « в » схемы электрической сети ( в = 1,3). Действительно,

А Э = Е I B2 ( t ) Г в = 1 Г в Т I B ( t ) = в                    в t = 1

= ( 4 - ( 13² + 36² + 20 2 ) + 2 - ( б² + 16² + 10² ) +

+ 3 - ( 2² + 10² + 5² ) ) - 8 - 0,001 =

= 69,04 кВт/ч.                           (22)

Из сопоставления результатов расчета потерь А Э методом с ортогонализацией базиса и суммированием потерь энергии на ступенях графиков нагрузок следует, что значения потерь электроэнергии АЭ совпадают с методом ортогонализации базиса.

Практическая значимость

Особенностью данной задачи является применение таких моделей определения потерь электроэнергии, которые обеспечивают независимую от разнородности узловых нагрузок точность определения потерь (21)–(22) в схемах электрических сетей.

Заключение

Рассмотренные модели определения потерь электроэнергии на отрезке времени Т, позволяющие распределить потери электроэнергии, а не мощности, по узлам(потребителям), являются актуальными в условиях развития отечественного электроэнергетического рынка.

Используя коэффициенты матрицы C , можно визуализировать распределение потерь в схеме сети между узлами потребления и производства электроэнергии.

При значимых нагрузках в узлах схем электрических сетей модели определения потерь электроэнергии за время Т с ортогонализацией базиса задачи являются точными, что подтверждают соответствующие результаты эксперимента (21) и (22).