Моделирование потока заряженных частиц применительно к процессам газоочистки

Изучение процессов управления многими системами связано с моделированием потоков заряженных частиц и электрических полей. Особенно большое практическое значение такие исследования имеют для оптимального управления электроприводами, электростатическими устройствами очистки газов, агрегатами для покраски крупных объектов, металлургическими процессами (в частности, электролизом алюминия и других металлов), что позволяет эффективно использовать энергию электрического тока.

Моделирование электрических полей дает возможность изучать электрические и магнитные потоки, а также потоки заряженных частиц (пыли, газов), что актуально как для разработки новых датчиков, так и для проектирования промышленных фильтров.

В современном математическом моделировании все более распространяются алгоритмы, известные под общим названием «методы частиц» [1]. Характерной особенностью этих методов является специальный способ дискретизации, при котором вводится множество дискретных объектов – модельных частиц, рассматриваемых как некоторая сетка подвижных узлов. Методы частиц применяются к задачам, в которых рассматривается эволюция во времени некоторой среды либо результат такой эволюции (см., например, работы [1, 2] и ссылки в них).

Общей характерной особенностью методов частиц является концепция перехода к дискретной аппроксимации. Она состоит в модельном представлении среды в виде конечного множества индивидуальных элементов – частиц, прямо или косвенно взаимодействующих друг с

другом. Каждая частица становится носителем некоторого набора характеристик – атрибутов данной среды, таких как электрический заряд, инертная или гравитирующая масса, импульс, завихренность, кинетическая энергия и т.п.

В методах частиц различают чисто лагранжевы и смешанные, эйлеро-лагранжевы или по-лулагранжевы алгоритмы. Алгоритмы первой группы сводятся к численному интегрированию систем дифференциальных уравнений динамического типа [2], которые описывают траектории взаимодействующих частиц. Для смешанных алгоритмов характерно то, что эволюция системы частиц на каждом временном шаге разбивается на два этапа. На одном из них при фиксированном положении частиц предварительно вычисляется результат их взаимодействия и (или) их коллективного воздействия на среду. Расчет ведется на неподвижной (“эйлеровой”) сетке. Поэтому этап называется эйлеровым. На другом, лагранжевом, этапе выполняется интегрирование на очередной временной шаг динамической системы, правая часть которой вычислена на эйлеровом этапе.

В работе [3] авторами был предложен алгоритм моделирования потоков заряженных частиц в электростатическом поле, относящийся к смешанным алгоритмам, на эйлеровом этапе которого вычисляется потенциал и напряженность электростатического поля с помощью уравнений Максвелла. На лагранжевом этапе строятся законы движения частиц в виде квадратичных сплайнов. Каждый участок сплайна находится путем дискретизации вектор-функции напряженности и интегрирования уравнений движения заряженных частиц в электростатическом поле.

Целью данной работы является моделирование движения заряженных частиц в электростатическом поле электродов применительно к процессу очистки отходящих газов. Для моделирования движения макроскопических заряженных частиц в электростатическом поле авторами использован тот же метод, что и в [3]. Данный метод применен для моделирования движения частиц пыли через пластинчатый электрофильтр.

Cтатья включает в себя три параграфа. В первом параграфе описывается моделирование потенциала и напряженности электростатического поля (эйлеров этап). Второй параграф посвящен построению модели движения заряженных частиц с помощью сплайнов. В третьем параграфе рассматриваются вопросы применения предложенного метода для компьютерного моделирования потоков заряженных частиц пыли в отходящих газах через электрофильтры при производстве цемента.

Моделирование потенциалаи напряженности электростатического поля

Напряженность электростатического поля определяется как антиградиент потенциала поля f

E = - grad f .

Согласно уравнениям Максвелла для электростатического поля [4]

- div E = div(grad f ) ≡     +     = 0 .

∂x2   ∂y2

Таким образом, потенциал f удовлетворяет уравнению Лапласа в области xe( - d/2, d/2), ye(0,11) (рис. 1) и граничным условиям f-d/2, y) = q 1(y), f(d/2, y) = q2(y), f(x, 0) = f(x, 11) = 0, где q(y), q(y) - дважды непрерывно дифференцируемые функции на отрезке [0,11], q(y) = q и q2(y) = qA при 8 < y < 11 — 8; q 1(0) = q 1( 11) = 0 и q2(0) = q2( 11) = 0. Здесь q - заряд на катоде, qА - заряд на аноде, δ – расстояние от края электрода до стенки емкости.

Математическая модель потока заряженных частиц

Будем считать, что частицы распределены равномерно на катоде. Поскольку вдоль оси z перемещений нет, мы будем рассматривать движение в плоскости xOy. Так как траектории движения заряженных частиц находятся в плоскостях, параллельных координатной плоскости xOy , для расчёта данных траекторий в пространстве используются компоненты скорости и ускорения по координатам x и у (рис. 1). При отсутствии столкновений заряженные частицы перемещаются под действием электрического потенциала с ускорением, равным m qE, где m – масса частицы [5]. Однако реальная траектория движения случайна, поскольку скорость и ускорение заряженной частицы в каждой точке ее траектории зависят от случайных столкновений с другой заряженной частицей или стенкой ёмкости, являющейся диэлектриком. Поэтому в каждой точке рассчитывается свой вектор ускорения, который затем используется для определения скорости в этой точке.

В основу математической модели движения заряженной частицы положены законы движения электрона под действием электрической силы. Для каждого участка траектории строятся отдельные уравнения движения, с помощью которых находятся координаты и скорость частицы в любой момент времени t .

Пусть частица достигает второго электрода за время T , т.е. t изменяется в промежутке от 0 до T . Уравнения движения частицы имеют вид [4]

d2

m ■ dX = q ■ E_x,                                                          (1)

dt

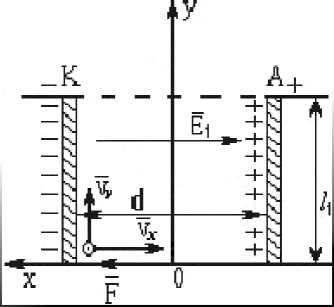
Рис. 1. Движение частицы: 11 - длина пластин электродов; d - расстояние между пластинами; vx, vy -проекции вектора скорости по осям X и Y; К – катод; А – анод d2 Уг

S = q ■ Ey

Для однозначного определения закона движения необходимо задать начальные условия:

x (0)=x , x '(0)=v 0 x,(3)

У(0)=У У‘(0)=v(4)

у

Напряженность электростатического поля зависит от координат точки между электродами, в которой находится частица в момент времени t , т.е. от координат x , у и, следовательно, от t . Поэтому решение задачи Коши (1) – (4) построим приближенно с помощью сплайнов.

Рассмотрим промежуток времени A t настолько малый, чтобы на участке траектории движения частицы от точки ( x(t ), y(t )) до точки ( x(t + A t ), y(t+ A t )) напряженность E = ( E x , E y ) можно было приближенно считать постоянной.

Как известно (см. [5] гл. 1), при однородном заряде q и постоянной напряженности E система кинематических уравнений плоского движения частицы в электрическом поле имеет вид q • E t2

x =----" — + v 0 xt + x 0, m 2

q • E y¹ y = m " 2 ⁺ v 0 y t ⁺ y 0 "

Используя эти уравнения, можно описать приближенную модель закона движения заряженной частицы вектор-функцией S(t) = (Sx(t) S (t) , где Sx(t) и Sy(t) - это квадратичные xy сплайны, построенные на сетке »: t.a t,i = 1 ,,, n = T /A t. На каждом промежутке [ t, t,„J сплайны Sx (t) и Sy (t) задаются функциями Sx (t) и Sy (t), которые являются решением задачи Коши (1) – (4) с

Ex=Exi^EAS-;4tlYS-;xo,

E y = E y, = E y ( 5 : ( t i) , S y ^{- 1} ( t i ))

и начальными данными

S X ( t i ) = S X * ( t i ), xi x i

^S y ( t i ) = ^S y ( t i )-

Таким образом,

+                                                      (5)

s y ( t ) = qm (L^ + v„ ( t - 1, ) + s y₍ t,).                                6,

Если происходит столкновение двух частиц с массами т и т^ в момент t * G [ ц, t _{t + 1} ] , летящих со скоростями v ( t *) и v 2 ( t *) (рис. 2), то траектория первой частицы меняется по следующему закону:

qEx (t-t)2

mi six (t)=^ qEx (t- t *)

mi    2

+ vix (t -1,) + S\.? (t), 1 x i 1 x i

+ v x ( t — t *) +

qEx (t^zti^L+ m1     2

t , < t <  t * ,

+ v L( t * - 1 ,) + s '-¹ ( t ,) , 1 x              i           1 x i

t * <  t <  t_M;

s 1 y ( t ) 4

qE y ( t - ti)²

m qEy (t -1*) mi     2

2 , 2

+ v ; _y ( t - t i ) + s ^c t i ) ,

+ v y ( t -t *) +

qE y ( t * - t i )²

m 1     2

+

t_t < t <  t * ,

+ viy (t * -ti) + sii--1(ti), t * < t < ti+1-

Аналогично изменяется траектория второй частицы:

^qE x ⁽ t ” ti ^{) 2}

m ²     .

S 2 x ( t ) = ] qEx (£ - t *)

2 , 2

⁺ v 2 x ⁽ t ~ ti ) ⁺ S 2 x ¹⁽ t i ),

t i <  t <  t *,

m 2    ²

+ v 2 x ( t - 1 *) +

qE x ⁽ t * ^— t i ^{)2 m} 2    ²

+

' i - 1

+ vix ( t * — ti ) + Six ( ti ), 2xx ix       2x    i/>

t* < t < t , ■

¹ — ¹<  i + 1 ;

_S ( _t ) = qEy ( t - t *)²

^{2 yV}--

qE y (t-^ i )- + v 2 y ( t - t -) + s 2 ^-; ( t -), m 2

t, < t <  t *,

m,    2

+ v 2 y ( t - t *) +

qE y ( t * - t i )²

^m 2    ²

+

+ V 2 y ( t * - t i ) + s 2^-1 ( t i ),

t * <  t <  t i + 1 .

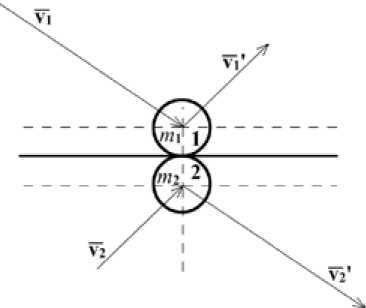
Рис. 2. Столкновение двух частиц: m 1 , т 2 - массы частиц; v 1 , v ₂ - скорости движения частиц до столкновения; v 1 ', v ₂‘ - скорости движения частиц после столкновения

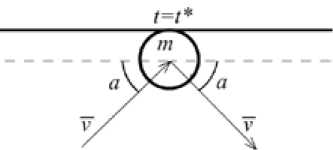
Рис. 3. Изменени                                                                цы; v - скорость

движения частицы; a – угол падения частицы

После столкновения скорости частиц у 1 = ( v _{1 x} , v ’ y ) и v ₂ = ( v ₂ x , v ₂ y ) равны

2m2v2 + (ml - mJv v2 = 2mivi + (m2 - mi)v2 , ml + m 2

соответственно, где v 1 = ( v ix , v iy ) и v 2 = ( v 2 x , v 2 y ).

При ударе частицы о стенку емкости угол падения частицы на стенку будет равен углу отражения от нее (рис. 3).

В этом случае траектория движения частицы моделируется следующим образом:

S X ( t ) 4

qE^ ⁽ t - t - ⁾²

I m 2

qExL ⁽ t t i ) + v ( t _ t ) + s - 1 ( t ), 2 x            x

- v X ( t - t *) + qE ⁽ t - t i ) + v X ( t * - t i ) + S X ^{- 1} ( t i ), m 2

t, <  t <  t *, t * <  t <  t i + i ;

^{5, 1} t ⁾ I q b (t ^- *² m 2

qE- ^+vy (t -1,)+s;H t,), m2 qE-G 2-tY              ,

+vi (t -1*)+(t—ti2-+vi (t * -1,)+S'-1 (t,), y          m 2 y           y

t , < t <  t *,

t * <  t <  t + 1 -

После удара частицы о вертикальную стенку меняется знак проекции v_y на противоположный, и траектория движения определяется по закону

S X ( t ) = ^

q^E xi ⁽ t  t i ⁾²

I m 2

^qExL (t-^t i )²- + v X ( t ~ t.) + S X ^{- 1}( t , ), m 2

+ V x ( t - 1 *) + qE xi- (t^^tit + v X ( t * - 1 , ) + S X ^{- 1}( t , ), m 2

t, < t < t *, , t * < t < t+i;

s i (t ) = i „

^A     qEy. ⁽ t - t * ^{) 2}

q b < t ^ + v y ( t - 1, ) + S_?( t,), ^m

m 2

qE ²

^- v y ⁽ t - t *) ₊ ^q-^ (-^^i^ ₊ v x ⁽ t * ^- ti) ₊ S ;*⁽ t i ),

t , < t <  t *, t * <  t <  t i + i -

В любом из описанных случаев координата z остается постоянной, то есть z = z^.

Моделирование движения частиц пыли в электрофильтре

Электрофильтры применяются в тех случаях, когда электрические свойства взвешенных частиц позволяют достичь высокой степени очистки. Электрофильтры обеспечивают выделе-– 647 – ние из газовых потоков мельчайших частиц пыли и тумана. Действие электрофильтров основано на ионизации газа между двумя электродами с образованием положительно и отрицательно заряженных ионов.

Для этого к электродам подводится постоянный электрический ток высокого напряжения мощностью 50-80 кВт. При высокой разности потенциалов газ между электродами ионизируется полностью, и происходит его слабое свечение наподобие короны вокруг электрода, присоединенного к отрицательному полюсу источника тока. Такой электрод обычно называют коронирующим электродом. Отрицательно заряженные ионы движутся к противоположно заряженному электроду, который называется осадительным [6].

Если газовый поток содержит частицы пыли или тумана, то отрицательно заряженные ионы адсорбируются на их поверхности и увлекают эти частицы к осадительному электроду. На поверхности электрода частицы отдают свой заряд и отделяются от электрода или падают при механическом встряхивании.

В электрофильтрах очистка газов от пыли происходит под действием электрических сил. В процессе ионизации молекул газов электрическим разрядом происходит заряд содержащихся в них частиц (коронирующий электрод). Ионы абсорбируются на поверхности пылинок, а затем под действием электрического поля они перемещаются и осаждаются к осадительным электродам. Зарядка частиц в поле коронного разряда происходит по двум механизмам: воздействием электрического поля (частицы бомбардируются ионами, движущимися в направлении силовых линий поля) и диффузией ионов.

Величину заряда q (кА), приобретаемого проводимой частицей сферической формы под воздействием электрического поля, рассчитывают по формуле [6]

q = 3пd42£0E, где 8о - диэлектрическая проницаемость

Е – модуль напряженности электрического поля коронного разряда, В/м.

ют по формуле

q = 3е /(е + 2)п d42e0 E, где ε – относительная диэлектрическая проницаемость частицы.

В пластинчатых электрофильтрах газоочистки электроды расположены параллельно друг другу, и движение частиц пыли происходит под воздействием поля электродов в потоке воздуха, образующегося за счет тяги трубы.

При параллельном расположении электродов Ex = 0, а следовательно, и v₀x = 0. Тогда система уравнений плоского движения частицы на отрезке [0,11] примет вид

(t) = xо, q • E

S^ t) =      • у + v о yt + У o.(16)

m2

Далее каждый участок сплайна будет рассчитываться следующим образом:

SX (t) = xo,(17)

Sy (t) = qEyi- (Mi)- + Vy,(t -1,) + Sy^-1(t,),  i = 1,2,..., n .                       (18)

m2

Для компьютерного моделирования потока частиц в электрофильтре был создан эмулятор. Он разработан в интегрированной среде разработки приложений Delphi. Для построения графики используется библиотека для работы с 3D-графикой OpenGL (Open Graphics Library) [7].

Электрофильтр как область моделирования представляет собой пространство между катодом и анодом, окруженное стенками, являющимися диэлектриками, и геометрически имеет форму параллелепипеда. Построение области моделирования начинается с задания фона, затем строятся стенки, коронирующий и осадительный электроды с использованием векторной графики.

При расчете потенциала задача Дирихле заменяется пятиточечной разностной схемой для эллиптических уравнений [8], построенной на сетке с одинаковым шагом h по x и y. Данная схема является устойчивой. Разностная задача решается методом простых итераций:

f^k(i,j)

(fk^-1 (i -1, j) + fk^-1 (i +1, j) + fk^-1 (i, j -1) + fk^-1 (i, j +1)) 4

k = 1, 2, …,

где i - координата узла сетки по оси у, а j - по оси x. После этого элементы массива f используются для вычисления компонент вектора напряженности с помощью разностных производных

Ex ( ) . ^f(ij-^ V^,j+ 1) , <

. Ey(lj * f(ij)- h(‘+1, j ’ и построения траектории полета заряженных частиц.

Начальное положение заряженной частицы моделируется генератором псевдослучайных чисел. Координаты частицы (x 1, у 1, z0) и средняя скорость перемещения частицы в точку с этими координатами в момент времени t моделируются с помощью уравнений (15)–(16). Затем осуществляется проверка принадлежности смоделированных координат области моделирования. Случай, когда координаты не входят в область моделирования, означает либо приход частицы на анод, либо удар о стенку емкости. Во все последующие моменты времени законы i движения частиц строятся в виде квадратичного сплайна (5)-(14), где Sx (t) удовлетворяет соотношению (17).

Если не смоделирован приход частицы на анод, моделируется столкновение частицы со стенкой емкости. Если в данный момент времени координаты моделируемых частиц совпадают, моделируется столкновение частиц. Когда координаты частицы совпадают с координатами анода, частица стирается, происходит осаждение.

Численный эксперимент моделирования применительно к процессу газоочистки проводили для электрофильтра ЭГАВ 1-40-9-6-4, который используется на Красноярском цементном заводе (ООО «Красноярский цемент») для очистки отходящих газов. Параметры электрофильтра представлены в таблице.

Таблица. Техническая характеристика электрофильтра ЭГАВ 1-40-9-6-4

п/п	Наименование параметра	Ед. изм	Величина
	Площадь активного сечения	м2	97,9
	Площадь осаждения	м2	11310
	Запыленность очищаемых газов, не более	г/м3	80
	Выходная запыленность газов, не более	мг/м3	50
	Температура очищаемых газов	0C	210-250
	Расстояние между осями одноименных электродов	мм	300
	Напряжение, поддерживаемое на электродах	кВ	50-80
	Энергетические затраты на очистку 1000 м3 газа	кВ ч/1000 м3	0,6
	Размер частиц	мкм	1-100

б

Рис. 4. Моделирование потока пыли при работе электрофильтра ЭГАВ 1-40-9-6-4: а – поток заряженных частиц в электрофильтре; б – потенциалы коронирующего (слева) и осадительного (справа) электродов

На рис. 4 представлены результаты компьютерного моделирования потока заряженных частиц в электрофильтре ЭГАВ 1-40-9-6-4.

Как видно из рис. 4, заряд на электродах распределен равномерно, потенциалы электродов моделируются в плоскости координат x и y, потому что они не зависят от ширины электродов z. – 650 –

Для отрисовки потенциалов используются элементы массива f определяющие цвет потенциала в каждой точке поля.

При незначительной модернизации эмулятор можно использовать для моделирования электромагнитных полей.

Заключение

В работе были рассмотрены вопросы моделирования движения заряженных частиц в электростатическом поле электродов применительно к процессу очистки отходящих газов. Для моделирования использовали метод, относящийся к смешанным алгоритмам, в котором каждый участок сплайна находится путем дискретизации напряженности и интегрирования уравнений движения заряженных частиц в электростатическом поле. Данный метод применен для моделирования движения частиц пыли через пластинчатый электрофильтр. Проведены численные эксперименты по компьютерному моделированию потока частиц пыли в электрофильтре ЭГАВ 1-40-9-6-4. Результаты моделирования согласуются с характером процесса очистки отходящих газов.