Моделирование потоков ионов в процессе электролитического рафинирования

Изучение потоков ионов в электростатических полях представляет собой весьма актуальную научно-техническую задачу. Большое значение такие исследования имеют для повышения эффективности металлургических процессов, в частности электролитического рафинирования меди и других металлов. Кроме того, моделирование электростатических полей между поверхностями электродов помогает исследовать природу взаимодействия катода с анодом.

Перенос вещества в процессе электролитического рафинирования осуществляется по трем механизмам: путем молекулярной диффузии, миграции и конвекции. В соответствии с этим говорят о потоках диффузии, миграции и конвекции. Суммарный поток складывается из трех указанных потоков [1]. Данная статья посвящена вопросам моделирования миграционного потока ионов в электростатическом поле электродов применительно к задачам электролитического рафинирования.

В современном математическом моделировании все более распространяются алгоритмы, известные под общим названием «методы частиц» [2]. Характерной особенностью этих мето

Среди методов частиц различают чисто лагранжевы и смешанные алгоритмы. Алгоритмы первой группы сводятся к численному интегрированию систем дифференциальных уравнений динамического типа [3], которые описывают траектории взаимодействующих частиц. Для смешанных алгоритмов характерно то, что эволюция системы частиц на каждом временном шаге разбивается на два этапа. На одном из них при фиксированном положении частиц предварительно вычисляется результат их взаимодействия и (или) их коллективного воздействия на среду. Расчет ведется на неподвижной (“эйлеровой”) сетке. Поэтому этап называется эйлеровым. На другом, лагранжевом, этапе выполняется интегрирование на очередном временном шаге динамической системы, правая часть которой вычислена на эйлеровом этапе.

Для методов частиц, как правило, характерна относительно невысокая точность. Обычный уровень погрешностей составляет несколько процентов. Это результат установившегося компромисса между разумным объемом вычислительной работы и возможностью моделировать сложные явления. Такой подход дает существенную экономию машинного времени.

В отличие от упомянутых выше задач, решаемых методами частиц, где рассматриваемые процессы протекают за короткие промежутки времени и при высоких скоростях, процесс электролитического рафинирования занимает продолжительное время (не меньше трех недель) и считается медленно текущим. Это обусловливает выбор методов частиц-в-ячейках для моделирования данного процесса, поскольку они обладают большим запасом устойчивости и допускают относительно быстрое продвижение по эволюционной переменной. Однако из-за длительности данного процесса, что являтеся сушественным отличием от упомянутых выше работ, применение метода быстрого преобразования Фурье для расчета потенциала поля не оправдано вследствие существенного накопления погрешности с течением времени. Кроме того, в настоящей статье используется динамическая модель движения частиц, учитывающая особенности процесса электролитического рафинирования.

Математическая модель потока ионов металла в процессе электролитического рафинирования

В основу математической модели движения заряженной частицы положены законы движения иона под действием электрической силы. Предполагается, что частицы распределены равномерно на аноде. Для каждого участка траектории строят отдельные уравнения движения, с помощью которых находят координаты и скорость частицы в любой момент времени t . Поскольку вдоль оси z перемещений нет, мы будем рассматривать движение в плоскости x O у – 528 –

(рис. 1). Реальная траектория движения частицы случайна, поскольку скорость и ускорение заряженной частицы в каждой точке ее траектории зависят от случайных столкновений с другой заряженной частицей или стенкой ёмкости, являющейся диэлектриком. Поэтому в каждой точке рассчитывают свой вектор ускорения, который определяется напряженностью электрического поля и используется для расчета скорости в этой точке.

Напряженность электростатического поля определяется как антиградиент потенциала поля ^f (см. [2]) E = ^- grad f

Согласно уравнениям Максвелла

• - div E = divgradf ‘ f + ^ = 0.                                    (1)

Sy

Таким образом, потенциал f удовлетворяет уравнению Лапласа в области х е ( - d /2, d /2), y e (0, l 1 ) (рис. 1) и граничным условиям

• ^f (^- d ^{/2, y)} = q , ^f d /2, ^y) = q a , ^f xx , ⁰⁾ = ^{f (} x , l i ) = 0,                                       ⁽²⁾

где q а - заряд на аноде.

Пусть частица достигает второго электрода за время T, т. е. t изменяется в промежутке от 0 до T Рассмотрим промежуток времени Kt настолько малый, чтобы на участке траектории движения частицы от точки (x(t), y(t)) до точки (x(t+At), y(t+At)) напряженность E = (Ex, Ey) можно было приближенно считать постоянной. Тогда приближенная модель закона движения заряженной частицы представляет собой вектор-функцию S(t) = (Sx (t) S (t) , где Sx(t) и Sy(t) -y это квадратичные сплайны, построенные на сетке и: ti = iAt, i = 1,...,n, n = T / At. На каждом промежутке [ti, ti+i] вектор-функция S(t) задается функциями [2]

S x ( t ) = qm. (L^ + _{P b (} t - _{( J}+ s x - _{l (} ,)                                     ₍₃₎

S^l y ( t ) = qE¹- (t^ti^ + v_yi( t - 1 , ) + S y -¹( t , )-                                             (4)

m 2

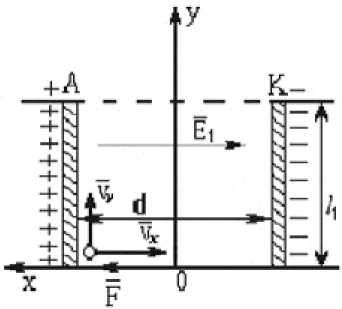
Рис. 1. Движение частицы: 1 1 - длина пластин электродов; d - расстояние между пластинами;

V x , V y - проекции вектора скорости по осям X и Y; К - катод; А - анод

– 529 –

Если происходит столкновение двух частиц в момент t * G [ t_t, t _{t +1} ], летящих со скоростями V (/*) и v₂ (/*) (рис. 2), то траектория первой частицы меняется по следующему закону:

qE x ( t i ) ( t - t i )²

m

5 1 х ( t ) U qE_x ( t i ) ( t - 1 *)

z"X

2 2

^{+ v} 1 x ( t - t i ) ^{+ х} 1 ( t i X

t i <  t <  t *,

m 1

+ v l x ( t - t *) +

qE x ( t i ) ( t - t i )² + m 2

i

,^{+ v} 1 x ⁽ t - t i ) ^{+ x} 1⁽ t i X

t * <  t <  t i +1 ;

qE y ⁽ t i ) ( t - t i )²

m

5 1 y ( t ) = b ^Ey ( t i ) ( t - t *) m 2

+ v 1y (t - t i ) + У 1 ( t i ),

⁺ v 1y (t ^- t *) ⁺

qE y ⁽ t i ) ( t - t i )² m 2

+

t i <  t <  t *,

+ Vly (t — ti) + У1(ti), t * < t < ti+1.

Аналогичным образом изменяется траектория второй частицы:

^qEx ⁽ t i ) ⁽ t ^— t i ^{) 2}

m

5 2 x ( t ) = ^ qE x ( t i ) ( t — t *)

^{+ v}2x ( t ^- t i ) ⁺ x 2⁽ t i X

t i <  t <  t *,

m 2

+ v 2 x ⁽ t ^- t *) ⁺

^qEx ⁽ t i ) ⁽ t ^— t i ^{) 2} + m 2

,^{+ v} 2 x ⁽ t ^- t i ) ^{+ x} 2⁽ t i X

t * <  t <  t i +i ;

^qEy ⁽ t i ) ( t — t i ) ²

m

5 2 y ( t ) = \ ^qEy ⁽ t i ) ( t — t *) m 2

^{+ v} 2 y ⁽ t ^- t i ) ^{+ y} 2 ⁽ t i ),

⁺ v 2 y ⁽ t ^- t *) +

^qEy ⁽ t i ) ( t — t i )² m 2

+

t i <  t <  t *,

+v iy(t- ti)+y2( ti)’ t * < t < ti+i.

При ударе частицы о дно электролитической ванны угол падения частицы на стенку будет равен углу отражения от нее (рис. 3). В этом случае траектория движения частицы моделируется следующим образом:

⁵х ( t ) = ^

qE_x ( t — t *)²

I m 2

qE_r t ²

— + v_rt + x _n, 2x и

( t *) ²

⁺ v x ⁽ t t ) ^{+ q} x 2 ⁺ v x t ^{+ x} ° ’

t < t *’ t * < t < t-+i;

qE_v ?²

—V + vyt + У °,                t < t *’ m2

qE_v U                     „ (Г*)²

— ⁽ „ ) — V y ( t — t *) + qE y,      + V y t * + y ° , t * <  t <  t i + i .

L m 2                       ■'2

В любом из описанных случаев координата z остается постоянной, т. е. z = z ₀.

Данная модель может быть использована для моделирования потока не только катионов металла, но и анионов кислотного остатка. В отличие от катионов металла анионы кислот- – 530 –

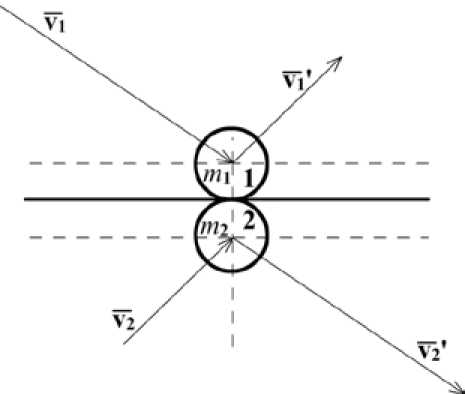
Рис. 2. Столкновение двух частиц: m 1 , m ₂ - массы частиц; v 1 , v ₂ - скорости движения частиц до столкновения;v1′, v2′ – скорости движения частиц после столкновения

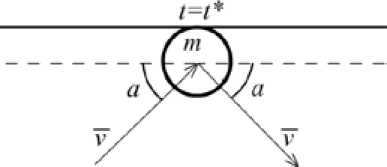
Рис. 3. Изменение направления движения частицы при ударе о стенку: m - масса частицы; v - скорость движения частицы; a – угол падения частицы ного остатка при миграции свободно движутся в электролитической ванне, не осаждаясь на электроды.

Компьютерное моделирование потока ионов

Ионы меди являются заряженными частицами одного и того же типа и имеют одинаковую массу. Для таких частиц массу не учитывают и берут равной единице для всех частиц. В начальный момент времени заряженная частица находится в точке (0, y ₀, z₀). В случае соударения частиц или удара частицы о стенку емкости траектории движения частиц формируются по законам (3)-(10) с m =1.

В электролизной ванне электроды расположены параллельно друг другу. При таком расположении электродов v ₀ x = 0. Начальные координаты y ₀, z ₀ заряженной частицы моделируются методом Монте-Карло как случайные величины, подчинённые равномерному закону распределения. В силу кинематических уравнений (6), (7) плоского движения частицы при постоянной напряженности электростатического поля первый участок сплайна рассчитывают по формулам (3), (4) при i = 1.

а)                                                       б)

Рис. 4. Моделирование потока ионов при электролитическом рафинировании:а – поток ионов меди и электролита; б – потенциалы катодов (темные) и анодов (светлые)

Далее моделируют координаты частицы ( x_b y_b z ₀) в момент t = 1 ₁ и среднюю скорость перемещения частицы в точку с этими координатами с помощью (3)–(10). Процесс продолжается до тех пор, пока частица не достигнет границы области моделирования. Когда частица достигает нижней горизонтальной границы области, моделируется ее столкновение с дном емкости. Если в какой-то момент времени координаты двух различных частиц совпадают, то моделируется столкновение частиц. В случае совпадения координат частицы с координатами точки на катоде происходит осаждение.

Область моделирования представляет собой пространство между чередующимися катодами и анодами, заполненное электролитом (рис. 4). Оно окружено стенками и дном ванны, являющимися диэлектриками. Область имеет геометрическую форму параллелепипеда.

Заряд на электродах предполагается распределенным равномерно с одинаковой плотностью, как в [2]. Потенциалы электродов моделируют в плоскости координат х и у , потому что они не зависят от ширины электродов z . Для расчета потенциала используется пятиточечная разностная схема для задачи (1), (2), построенная на сетке с одинаковым шагом h по x и у [6].

Для моделирования потока ионов меди между катодом и анодом в электролизной ванне было разработано CAE-средство [2].

На рисунке 4 представлены результаты моделирования потока катионов меди и анионов кислотного остатка для лабораторной электролизной ванны при стандартном напряжении 0,2 В с тремя катодами и двумя анодами.

Заключение

Создан алгоритм, позволяющий применять метод частиц-в-ячейках для моделирования потока ионов между анодом и катодом при электролитическом рафинировании. Метод приме -нен для моделирования потоков ионов металла и кислотного остатка в лабораторной установке электролитического рафинирования меди, проведены численные и компьютерные эксперименты по компьютерному моделированию.