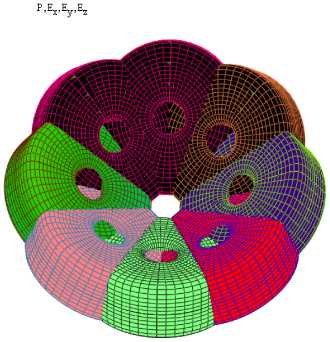
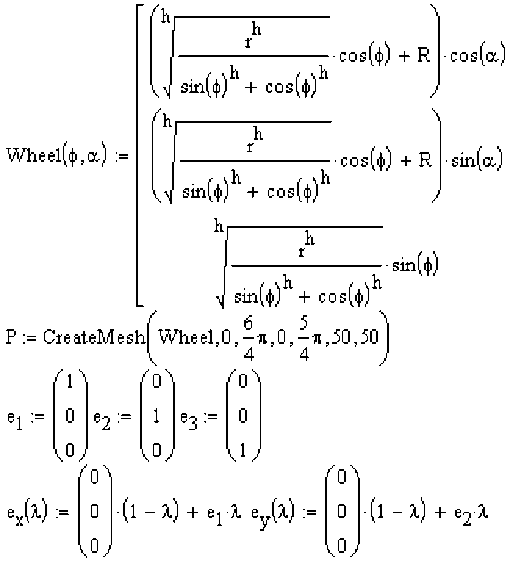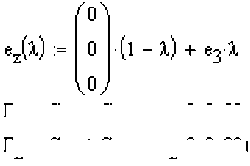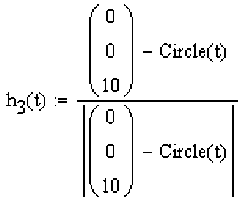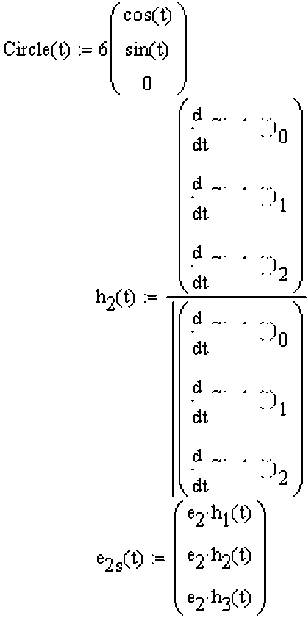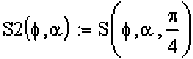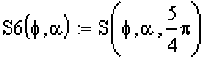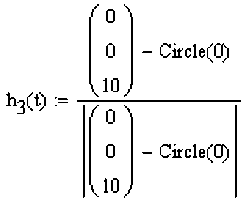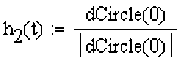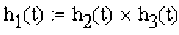Моделирование поверхностей в системе компьютерной математики Mathcad

Многие инженерные задачи связаны с конструированием, кинематикой и анимацией поверхностей, в том числе поверхностей, где присутствуют элементы вращения. В связи с этим разработчики вынуждены вникать в пространственные задачи преобразования поверхностей, что не является их непосредственной функцией. Данная статья не претендует на универсальность подхода к решению моделирования поверхностей вращения, но иллюстрирует, что при сложности поставленной задачи некоторые моменты можно наглядно продемонстрировать в системах компьютерной математики (в данном случае MathCAD 11).

Вращение параметрической кривой вокруг прямой, произвольно расположенной в пространстве

Рассмотрим простую задачу: получить уравнение поверхности вращения произвольной параметрической кривой вокруг прямой, произвольно расположенной в пространстве.

Вращаемая параметрическая кривая задана в виде: _R(t) _

x(t)

y(t)

. Ось вращения задана двумя

z(t)

точками A и B (рис. 1). Основанием перпендикуляра, опущенным из точки R(t) на прямую

-                    .      .    ( r (t) -A ) • (в - A) -   -

A B , будет точка P(t) = A -I-- - —--- -—- — (B - A) . Определим локальный базис для

"                       (B-A) (B-A)

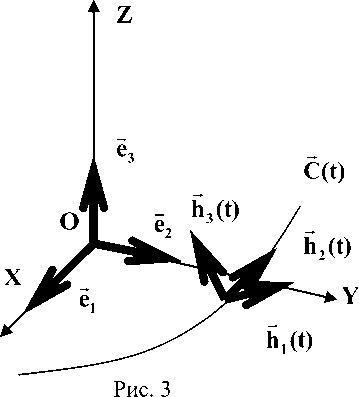
каждой отдельной точки R(t) . Это тройка векторов (h₁(t),h₂(t),h₃(t) ) с центром координат в

-        -      R(t) — P(t)  —      B_ A — точкеP(t), где hj(t) = — ---.., h3(t) = ——4, h2(t) = h3(t)xhj(t).Если мы захотим вра-

I R(t)-P(t)|            |b-a|

——                                    ——                                                     ——        ——         —— щать точку R(t) вокруг точки P(t) в системе координат (h1(t),h2(t),h3(t)) , то это будет пло- ская окружность s (w, t) =

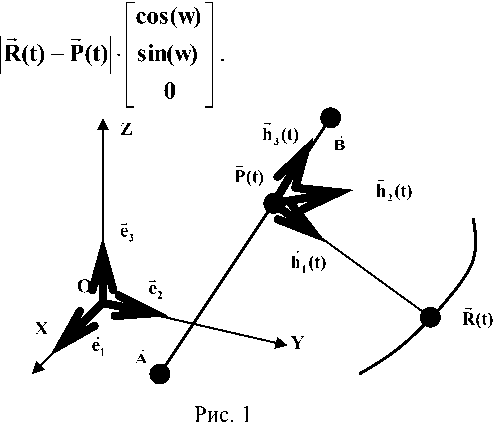
Перенос окружности в систему координат (OXYZ)

и вращение непосредственно во-

—— круг точки P(t) осуществляется следующим образом: S(w, t)

^— is (t) ^— (w, t)

^— 2s (t) ^— (w,t)

e 3s (t) s (w,t)

——

P(t) .

Базис    (MtM 2 _S ^(t ),e 3s ^(t))    рассчитывается по формулам:    ^— _{х s}(t) =

^— 2s (t) =

—— e2

—— e2

—— e2

—— h1(t)

—— h2(t)

—— h3(t)

—

,

—

координат

^— 3s (t) =

—— e3

—— e3

—— e3

—— h1(t)

—— h2(t)

—— h3(t)

—

—— e1

—— e1

—— e1

—— h1(t)

—— h2(t)

—— h3(t)

,

, так векторы (^—₁ ,е₂ ,е₃) будут выглядеть из системы

(h 1 (t),h 2 (t),h 3 (t) ). Базисные векторы ( — ,e₂, e,) системы координат (OXYZ) (см.

рис. 1) имеют значения e2 =

,

—— e2

,

—— e3

. Более подробно вопросы преобразова-

ния базиса рассмотрены на интернет-ресурсе во вкладке «Преобразование базиса». Ниже приведен листинг программы, выполненной в системе MathCAD 11.

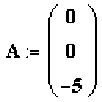
В :=

2 I          f °

3 R(f) := sin(2f) + 3

5 J        \ 3cos(f)

P(>a+MM(IM

(B-A)(B-Aj '

Входные данные: ось вращения и вращаемая кривая. В программном коде для получения корректного результата рекомендуется производить изменения значений только этих параметров.

Рассчитывается основание перпен-

—

—

дикуляра P(t) из точки R(t) на пря-

— мую A B .

R(f)-P(f)

1Г |R(f)-P(f)|

_Wi, - ^B"^A

^W" |B-A| ty^^l1!»

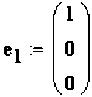
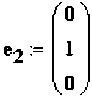
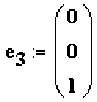
^М^ c2s^ := ^'^^

l^W;

^3hl^)

e2s^ :=

2-hi(f)> e₂ 112(f)

Локальный                базис

(h₁(t),h₂(t),h₃(t) ) для каждой отдельной точки R(t) .

Базисные векторы (е_х ,е₂ ,е₃) системы координат (OXYZ) .

Базис ( e _1s(t),e _2s(t), e _3s(t)) в системе координат (hj (t), h₂ (t), h₃ (t) ).

e3s^ := ^ Лг^ ^W

'cos(w) ^

s(w,f) := |R(f) - P(f)| ■ sin(w)

к 0 j

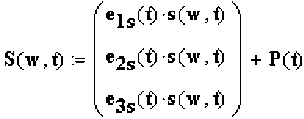
S , Line , R

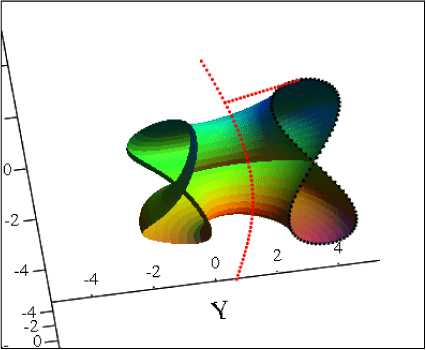
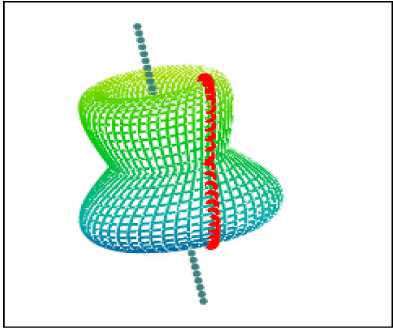
Вращаемая точка R(t) описывает e e окружность вокруг прямой A B .

Ее представление в системе коорди-—►        —►         —►

нат (h1(t),h2(t),h3(t)) .

Та же окружность, представленная в системе координат (OXYZ) .

e e

Прямая A B .

Результат построения поверхности вращения кривой R(t) вокруг прямой ^{e e}

A B , представлена в системе координат (OXYZ) .

Вращение одной параметрической кривой вокруг другой

Вращение производится в плоскости перпендикуляра, опущенного из точек вращаемой кривой на другую.

Пусть R(t) является вращаемой кривой (рис. 2). Рассмотрим кривую Q(t) . Из точек кривой R(t) опустим перпендикуляр на кривую Q(t) .

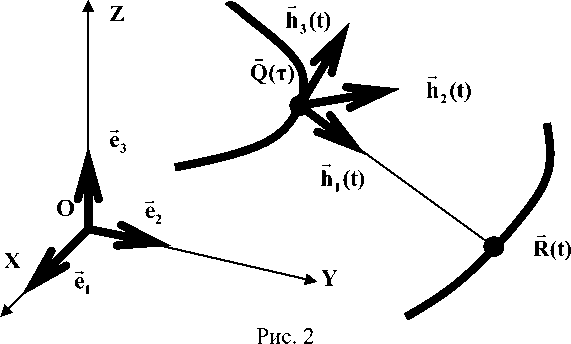
т параметрами t и

Соответствие между

происходит из уравнения

(R(t)-Q(T))□dQ(T) = о. Следует отметить, что далеко не всегда можно получить аналитиче-dT скую зависимость T(t). Решение данного уравнения в численном виде будем искать сле дующим образом. Скалярное уравнение F(t, т) = (R(t) - Q(t))[]dQ(T) продифференцируем по dT

,. д . д _.   , dT _ _ параметру t, предполагая, что существует зависимость T(t), —F(t, т)+—F(t, т)   = 0. От- t        St       dt

V     dT    ^F(t’T)

сюда имеем исходные данные для постановки задачи Коши              , начальные ус- dt ^F(t, T)

ловия t0 и T(t0) = T0 получаем из решения уравнения (R(t)-Q(T)) DdQ^ = 0 любым известит ным способом.

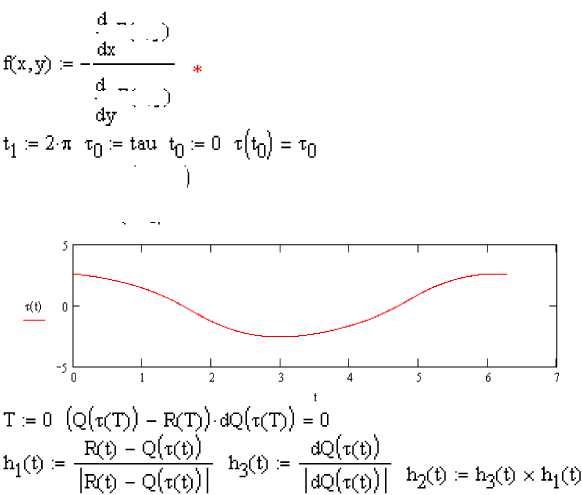
Таким образом, будем считать, что нами найдена функциональная зависимость параметра т от параметра t . В точке кривой Q(t) , соответствующей точке кривой R(t) , сфор-

——        ——         ——                       —► мируем локальный базис (h1(t),h2(t),h3(t)), где h3(t) =

R(t)-Q(t(T))

, h3(t) =

I R(t)-Q(t(T))|

-dQ(T(t)) dT ______ -dQ(T(t)) dT

,

h₂(t) = h₃(t) xhj(t) . Далее можно поступить так, как описано в 1: сформируем базис

^—

(^—₁ ,^—₂ ,e₃) в системе координат (OXYZ) , переведем его в систему координат базиса

——        ——         ——

, ——

——

—

(h _x (t),h ₂ (t),h ₃ (t) ), он будет выглядеть как (e,_s(t),e_2s(t),e_3s(t)) , формулы приведены в 1.2.

Вращение точки R(t) вокруг точки Q(t) в системе координат базиса (h₁(t),h₂(t),h₃(t) ) в плоскости векторов h₃(t) , h₂(t) будет описываться аналогичным способом, как в 1:

cos(w)

s(w, t) = |R(t) - Q(T(t))|[ sin(w) . А непосредственно моделируемая поверхность будет выгля- 0

els(t) s(w,t)

деть так: S(w, t) = e₂ s (t) • s(w, t) + Q(T(t)) . Ниже приведен листинг программы, иллюстри-

_ e₃ s (t) s(w,t)

рующей приведенный в этом параграфе способ вращения параметрической кривой вокруг

другой.

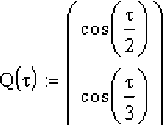
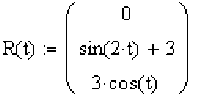
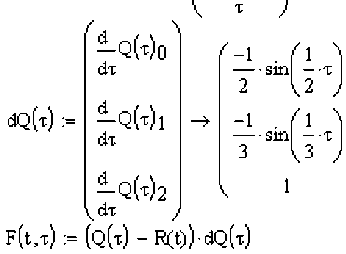
Входные данные: Q(t) и R(t) . В программном коде для получения корректного результата рекомендуется производить изменения значений только этих параметров.

Расчет вектора

dQ(T) dT

.

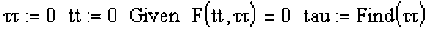
-F(x,y)

Формирование       уравнения

F(t, T) = (R(t)-Q(T))□dQ(T). dT

Нахождение начальных условий для задачи Коши.

Given -^(t) = f(t,T(t)) т := Odesolve|t,ti 1

—F(x,y)

Задание дифференциального уравнения 1 порядка для решения задачи Коши.

Решение задачи Коши.

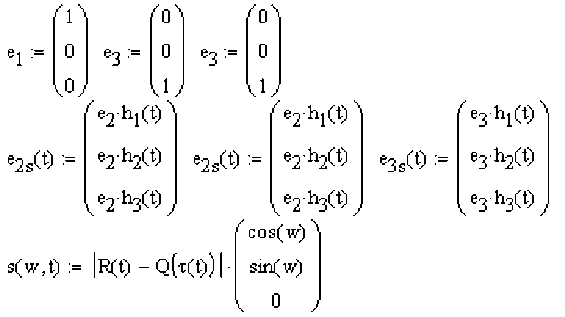
График зависимости параметра t от параметра t .

Тестовая проверка.

Локальный              базис

(h₁(t),h₂(t),h₃(t) ) для каждой отдельной точки R(t) .

Базисные векторы   (е₁, е₂, е₃)

системы координат (OXYZ) .

Базис (els(t),e2s(t),e3s(t)) в системе координат (h2 (t), h2 (t), h3 (t)).

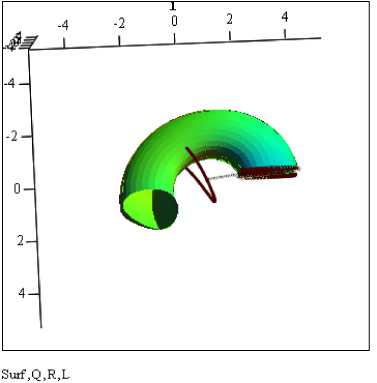
Вращаемая точка R(t) описывает окружность вокруг Q(T(t)) в плоскости векторов h_t(t) , h₂(t) . Ее

представление в системе координат

''els(t)-s(w,t)''

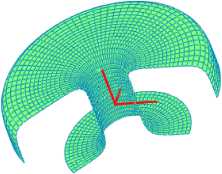
S(w,t) := e2s(9's(w,t) +Q(

^e3s(t)s(w,t)>

L(h) := h-Qto) + (1 - h)R(T)

Surf := CreateMesh(S ,0,1 я ,0,2 л ,50,50)

Q,R,L,Surf

Результаты работы программы, разные виды одной и той же поверхности.

——        ——         ——

(h1(t),h2(t),h3(t)).

Та же окружность, представленная в системе координат (OXYZ) .

Перпендикуляр, опущенный из точки R(0) на кривую Q(t) .

Визуализация поверхности.

Вращение параметрической поверхности вокруг прямой

Рассмотрим параметрическую поверхность x случае это поверхность вращения: W ф,а =5у z

в некотором

ф,а

Ф,а . Пусть

Ф,а

локальном базисе, в данном

центр координат локального

x базиса движется по некоторой траектории C t = y

z

t t (рис. 3).

t

Локальный базис ht, ht и ht в приведенном ниже примере передвигается по траектории Ct следующим образом. Параметрическая кривая Ct в нашем случае явля-cos t ется окружностью

C t = 6 sin t . Единичный вектор ht направлен по касательной к 0

кривой Ct : h t

Ct d dt

Ct d dt

. Единичный вектор ht совпадает по направлению с векто-

ром

-C t

: h₃

t

0
0	-C t
10
0
0	-C t
10

. Из условий постановки задачи очевидно, что векторы

ht и ht лее поступаем

ортогональны. Соответственно, вектор ht будет h t = h t × h t . Да-способом, описанным в § 1. Произведем преобразование базиса (е, ,е₂ ,е₃)

системы координат OXYZ в базис (eis(t),e 2S(t),e 3,(t)) . Так он будет выглядеть из системы координат базиса (h (t),h2(t),h3 (t)). Передвигаемая поверхность W ф,а в зависимости от e1s W значения параметра t выглядит так: S ф,а,t = e2s W e3s W листинг программы иллюстрирует данные вычисления.

г := 2 R := 3 h := 6

Ф,а ф,а + C t . Приведенный ниже

Ф,а

Задание параметров передвигаемой поверхности W ф,а (в нашем случае это поверхность Wheel ф,а ).

Визуализация.

Задание и визуализация единичных векторов системы координат OXYZ .

E^ := CreateSpacel ex,0,2,20|Ey := CreateSpacei e^,0,2,201

E^ := CreateSpacel 6^,0,2,201

4s^:= elh2^ ei-h3(t)

—Circleft;

—Citclert)

—Circleft;

—Circlet t)

—Circlet t)

—Circlet tj hi(t) := h2(-

^eis(t) -Wheelie,)

Задание траектории перемещения Ct (Center t ).

Задание локального базиса.

з(ф,а,д) :=

e2 s(t) • Whe е1(ф, a,)   + Circle(t)

e3s(t) Wheeled)

Визуализация поверхности

t=

0ππ42

31 (ф,а) := 3(ф,а,0)

35(ф,а) := з(ф,а,л)

Pl

РЗ

Р5

Р7

Wheel φ,α

3π

= CreateMesh(Sl,0,2n,0,2n,50,50)

= CreateMesh(S3,0,2n,0,2n,50,50)

= CreateMesh(35,0,2n,0,2n,50,50)

= Сгеа1еМезН(37,0,2л,0,2л,50,50)

Перерасчет локального базиса.

Передвигаемая поверхность

Wheel φ, α    по траектории

Center t в момент времени t .

от значений параметра

πππ

π5 3  7

37(ф,а) := 3

34(ф,ос) := з[ ф,а.,-л

V    4

38(ф,а) :=з[ф,а,-л \     4

Р2 := CreateMesh(S2,0,2n,0,2n,50,30) Р4 := CreateMesh(S4,0,2л ,0,2л ,50,50) Рб := Сгеа1еМевЬ(Зб,0,2л,0,2л,50,50)

Р8 := Сгеа1еМесН(38,0,2л,0,2л,50,50)

Поверхность Wheel ф,а в локальном базисе.

Р1,Р2,РЗ,Р4,Р5,Р6,Р7,Р8

Результат передвижения поверхности Wheel ф,а при различных значениях параметра t .

N := 50

л •   • А \ Ji FRAME

Animation^,а.) := 51 ф,а,,———2л

Cinema := Cre ateM е sh(Animation, 0,2л,0,2л,50,50)

Среда MathCAD предполагает создание анимированных изображений.

Если в системе координат OXYZ (см. рис. 3) зафиксировать локальный базис (h (t), h (t), h (t)) , мы получим результат, показанный ниже. Еще раз напомним о том, что должно выполняться требование ортогональности локального базиса. Векторы (h (t), h (t), h (t)) должны быть единичными. Параметрическая кривая Ct и ориентация в системе координат OXYZ локального базиса (h (t), h (t), h (t)) может быть произвольной.

Данный результат достигается в листингепрограммы следующим образом:

dCircle(t) :=

-Circle(t)n dt и

-CircleCt). dt 1

Р1,Р2,РЗ,Р4,Р5,Рб,Р7,Р8

-Circle(t)-

Анимированное изображение можно посмотреть здесь

Если в системе координат локального базиса (h (t), h (t), h (t)) пожелаем произвести вращение исходной поверхности вокруг оси ординат, то нам необходимо уравнение исход- ной поверхности

умножить на матрицу вращений вокруг оси Y :

Wh φ,α,ω =

cos ω	0	sin ω
0	1	0
-sin ω	0	cos ω

Wheel φ, α . Листинг программы можно скачать здесь.

Результат работы программы, в которой вращение вокруг оси ординат локального базиса синхронизировано следующим образом: ω t =  , показан ниже. Сам локальный базис

(h (t), h (t), h (t)) не вращается, вращается в нем только исходная поверхность Wheel φ, α .

Анимированное изображение можно посмотретьздесь

Также можно совершать одновременное вращение вокруг оси ординат и вокруг оси абсцисс локального базиса (h (t), h (t), h (t)) :

	1	0	0	cos ω	0	sin ω
Wh φ,α,ω,ψ =	0	cos ψ	sin ψ	0	1	0	Wheel φ, α
	0	-sin ψ	cos ψ	-sin ω	0	cos ω

Заключение

В данной статье мы продемонстрировали решение задач, связанных с моделированием поверхностей, в которых присутствуют элементы вращения. Также были решены некоторые кинематические задачи: задача движения поверхности по траектории с изменяемой ориентацией локального базиса, задача движения поверхности по траектории с вращением в локальном базисе. Решение было произведено в системе компьютерной математики MathCAD 11. Также были приведены программные коды всех примеров, изложенных в данной статье.