Моделирование позиционных характеристик индуктивных датчиков линейных перемещений модифицированными функциями Гаусса с разностным аргументом

Преобразователи линейных перемещений (ПЛП) являются одним из важных измерительных элементов высокоточных систем управления и контроля, особенно в авиационной и ракетнокосмической технике. Разработкой и выпуском точных и компактных преобразователей перемещения занимаются достаточно многие фирмы, но только очень немногие из них могут выпускать преобразователи для жестких условий эксплуатации (Heiden-hain, Германия; Sony и Mitutoyo, Япония; Harley Precision Instrument, США и некоторые др.). В связи с работами по модернизации и созданию новых типов ракетных, авиационных и наземных боевых комплексов вызывает необходимость в расширении исследований по созданию первичных преобразователей с высокими стабильными метрологическими показателями, в том числе устойчивыми к особо жестким внешним дестабилизирующим факторам: виброударным воздействиям, глубоким перепадам температуры вплоть до криогенных температур.

Для отработки конструкции преобразователей перемещений их оптимизации необходима математическая модель, которая могла бы аппроксимировать экспериментальные данные по возможности более точно с использованием небольшого количества коэффициентов, характеризующих модель. Анализ характера

экспериментально полученных позиционных характеристик U j показал, что следующие функции имеют вид, характерный для позиционных характеристик индуктивных преобразователей перемещения (ИПП):

Y 1 ( x ) = a + b ■ ( x ₀ - x ) ■ e c (^{x 0}   x

Y 2 ( x ) = a + b ■ ( x ₀ - x ) ■ e c x ⁰   x

Y 3 ( x ) = a + b • ( x ₀ — x ) ■ e ' ⁰    '

Y 4 ( x ) = a + b • sin g ( x ₀ — x ) ■ | x ₀ — x| ”

_e- ^c ■ x о ^{— x} l^Z

В качестве критериев оптимизации при поиске неизвестных коэффициентов a, b, c, x0, n, z функций (1)-(4) были выбраны минимальные значения среднеквадратического отклонения Wско, среднемодульного отклонения Wсмо и наибольшего отклонения Wммо во всем диапазоне перемещений Х подвижного (элемента) ИПП:

W 1 ( a, b, c, x ₀, z, n ) =

Nn — 1

Nn — 1

^ (U j — Y 1( a , X j , b, c, x 0 , z , n ))

j = 0

1 Nn — 1

W 2 ( a , b, c, x 0 , z , n ) = ——- У ( IU j — Y 1( a , x j ,b , c , x ₀, z , n )l) Nn — 1 t ~ 5

W 3 ( a , b, c , x ₀, z , n ) = Max ( U _y — Y ( x_} ))            (7)

где Nn – количество экспериментальных точек.

Коэффициенты a, b, c, x 0 , z, n можно найти минимизируя функцию погрешности W, используя компьютерный математический пакет Mathcad компании MathSoft [2] с помощью функции:

Minimize ( W,a,b,c,x , z , n)

В таблице 1 даны результаты расчетов оптимальных коэффициентов a, b, c, x 0 , z, n обеспечивающих минимальные погрешности аппроксимации функций Y1(x), Y2(x), Y3(x), Y4(x) для каждого критерия W^ско, W^смо, W^ммо. На рис. 1 графически представлена аппроксимирующая функция Y1(x) оптимизации по среднеквадратическому отклонению W^ско и исходный набор данных U j (x j ).

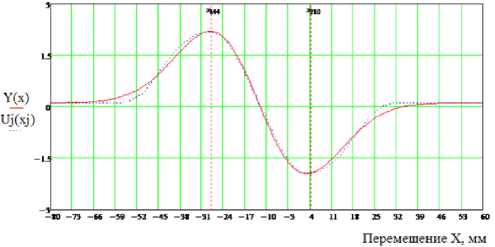
Рис. 1. Позиционные характеристики экспериментальной U j и аппроксимирующей функции Y1(x)

Относительные погрешности среднеквадратическое отклонения γ1 ско , средне модульное отклонение γ1 смо и наибольшего отклонения γ1 ммо для всего диапазона аппроксимации для функции Y1(х) (формула 1), оптимизированных на минимум среднеквадратичного отклонения определяются как:

γ1ссккоо =      00     ⋅W1ссккоо(a,b,c, x0) = 2,01%(9)

U -U maxmin

γ1сскмоо =    100    ⋅W1сскмоо(a,b,c,x0)=1,32%

— U maxmin

γ1ско =             ⋅W1ско (a,b,c,x ) = 5,2% ммо                             ммо ,  ,  ,  0

max - min

Относительные погрешности среднеквадратическое отклонения γ1 ско , средне модульное отклонение γ1 смо и наибольшего отклонения γ1 ммо для всего диапазона аппроксимации для функции Y1(х) (формула 1), оптимизированных на минимум среднемодульного отклонения определяются как:

γ1сскмоо =    100    ⋅W1сскмоо(a,b,c, x0) = 2,1% maxmin

γ1ссммоо =             ⋅W1ссммоо(a,b,c,x0)=1,24% maxmin

γ1смо =             ⋅W1смо(a,b,c,x ) = 6,14% ммо                         ммо0

maxmin

Относительные погрешности среднеквадратическое отклонения γ1 ско , средне модульное отклонение γ1 смо и наибольшего отклонения γ1 ммо для всего диапазона аппроксимации для функции Y1(х) (формула 1), оптимизированных на минимум максимального отклонения определяются как:

γ1ммо =    100    ⋅W1ммо(a, b, c, x ) = 2,16% ско                              ско0

max - min

γ1смммоо =    100    ⋅W1смммоо(a,b,c,x0)=1,38% maxmin

γ1ммо =    100    ⋅W1ммо(a, b, c, x ) = 5,01% ммо                             ммо ,  ,  ,  0

maxmin

Аналогично была проведена оптимизация функций Y2(x), Y3(x), Y4(x), результаты помещены в сводную таблицу 1. Распределение погрешности ε j аппроксимации функцией Y1(х) в каждой j-той экспериментальной точке вычислялось по формуле:

U -Y1(x ,a,b,c,x ) ε = j         j, , , , 0 ⋅100% j      U -U max     min

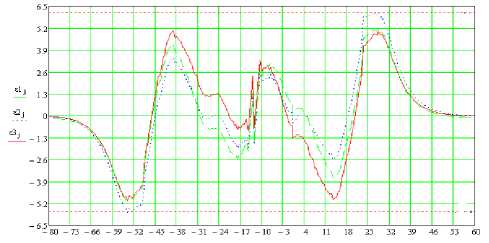
и представлена графически на рис. 2 ε1 j – при минимизации среднеквадратичного отклонения; ε2 j – при минимизации среднемодульного отклонения; ε3 j – при минимизации максимального отклонения.

Перемещение X, мм

Рис. 2. Относительная погрешность аппроксимирующей функции Y1(x)

Распределение погрешности ε j аппроксимации функцией Y2(х) в каждой j^-той экспериментальной точке вычислялось по формуле:

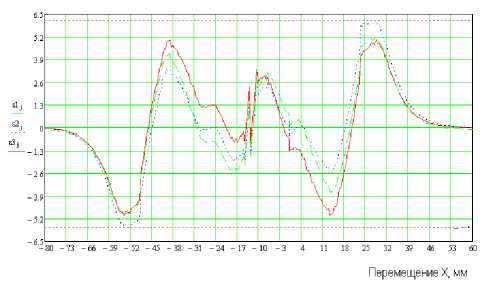
Рис. 3. Обобщенная погрешность аппроксимирующей функции Y2(x)

ε j

U: - Y 2( x, , a , b , c , x )

^v j’ ’ ’ ’ ⁰' . 100%

U -U ■ max     min

и представлена графически на рис. 3 ε1 j – при минимизации среднеквадратичного отклонения; ε2 j – при минимизации среднемодульного отклонения; ε3 j – при минимизации максимального отклонения.

На рис. 2, 3 показаны относительные погрешности аппроксимирующих функций Y1(x), Y2(x), из которых видно, что по краям экспериментальной характеристики погрешность аппроксимации максимальная, а в центральной области погрешность аппроксимации минимальная.

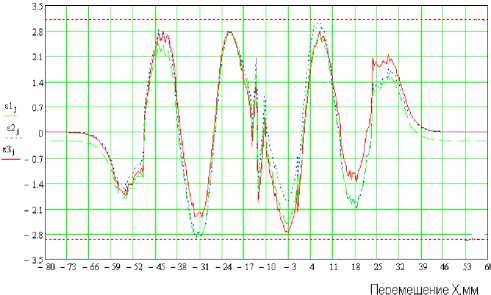
Рис. 4. Обобщенная погрешность аппроксимирующей функции Y3(x)

Распределение погрешности ε j аппроксимации функцией Y3(х) в каждой j^-той экспериментальной точке вычислялось по формуле:

U, - Y 3( x , a , b, c, x _n)

_£ = ^----- v j , , , , 0) _ _W0_%        (20)

j max     min и представлена графически на рис. 4 ε1j – при минимизации среднеквадратичного отклонения; ε2j – при минимизации среднемодульного отклонения; ε3j – при минимизации максимального отклонения.

Распределение погрешности ε j аппроксимации функцией Y4(х) в каждой j^-той экспериментальной точке вычислялось по формуле:

U_; - Y 4( x,, a, b, c, x )

_g = ^----- v j , , , , 0) _ _W0%         (21)

j      U -U max     min и представлена графически на рис. 5 ε1j – при минимизации среднеквадратичного отклонения; ε2j – при минимизации среднемодульного отклонения; ε3j – при минимизации максимального отклонения.

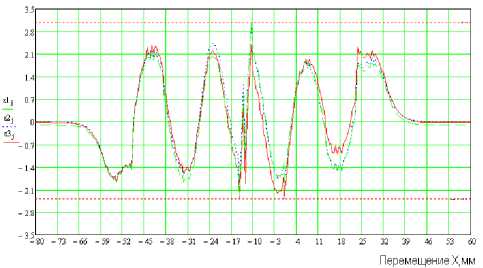
Рис. 5. Обобщенная погрешность аппроксимирующей функции Y4(x)

На рис. 4, 5 показаны относительные погрешности аппроксимирующих функций Y3(x), Y4(x), на которых видно, что по краям экспериментальной характеристики погрешность аппроксимации и в центральной области погрешность аппроксимации минимальные.