Моделирование привода динамического стенда авиационного тренажера

С точки зрения управления динамические стенды – многомерные объекты управления. Как объект управления шестистепенной динамический стенд – это система с управляемыми координатами по 6 степеням свободы: линейные перемещения по 3 взаимноперпендикулярным осям (продольное, вертикальное и поперечное) и 3 угловым движениям относительно этих осей (крен, тангаж и рыскание). При этом по каждой координате управление должно обеспечиваться положением, скоростью, ускорением и перегрузкой. Имитация перегрузок динамическим стендом должна осуществляться с требуемыми характеристиками в ограниченных конструкцией стенда пределах для угловых и линейных перемещений [1].

С целью повышения точности и повышения экономической эффективности предложен способ управления координатами динамического стенда, отличительной особенностью которого является единое управление в замкнутой системе перемещением, скоростью, ускорением и перегрузкой [2]. При предлагаемом способе воспроизведения акселерационной информации на вход следящего привода при воспроизведении, например, ускорения, подается сформированный сигнал, пропорциональный перемещению от действия ускорения по времени. При идеальной работе привода его исполнительное звено (шток) будет двигаться по квадратичной зависимости от времени в соответствии с изменением управляющего сигнала, воспроизводя тем самым реальные ускорения исполнительного звена. При этом следящий привод должен удовлетворять высокой точности отработки входного сигнала, быстродействию и плавности движения.

Рис. 1. Структурная схема формирования законов управления

Система управления динамическим стендом обладает инерционными свойствами, обусловленными наличием накопителей энергии, моментами инерции, массами, для перемещения которых не могут быть использованы

источники энергии бесконечно большой мощности. Обеспечение заданных характеристик динамического стенда по управлению возможно в общем случае в замкнутой системе n-порядка, показанной на рис. 1. Минимально возможный порядок системы, обеспечивающей формирование заданных законов управления динамического стенда в замкнутой астатической системе согласно предложенному способу, соответствует третьему. В то же время реальные системы приводов (гидропривода, электропривода) чаще всего могут быть описаны математическими моделями более высокого порядка.

С целью исследования основных характеристик динамических стендов и определения требований к их приводам при формировании заданных законов управления координатами: перемещением, скоростью, ускорением, перегрузкой - разработана имитационная математическая модель, обеспечивающая моделирование законов управления в замкнутой системе произвольного порядка с заданными показателями качества. Обобщённая имитационная модель динамической системы n -порядка, описывающая формирование законов управления в замкнутой системе по перемещению вектором управляемых координат X = [ x_{n — 1} x n x n _{+ 1} x n _{+ 2}] ^T , включающим координаты управления перемещением x _n+2, скоростью x _n+1, ускорением x _n, перегрузкой x _n-1 имеет следующий вид:

X =

x n — 1

xn xn+1

. xn + 2

0 0 L 1

0 0 L 0

0 0 L 0

00 L 0

	V 1 V 2
0 0 0 1	V 3
1 0 0	L
010 '	V 1
	n — 1
0 0 1	V n
	V n + 1
	V n + 2

V 1(1) "		- a„ — 2	_ an _
V 21)		1	0
V Р		L	1
V n !?1	=	0	0
V (1) n		0	0
V n + 1		0	0
V^ _		_ 0	0

-1

X

a 1

a 0

Л

X

^V 1

V 2

V 3

^V n - 1

+

^V n

^V n + 1

А

Л2

Синтез имитационной модели системы с формированием законов управления по предлагаемому способу выполнен на основе методов стандартных коэффициентов и динамической компенсации. Задание свойств системы обеспечивается выбором порядка системы n , коэффициента демпфирования ^, времени нарастания переходного процесса т.

Синтезированы математические модели третьего, шестого (с одним и двумя нулями), седьмого порядков и проведены исследования влияния на точность отработки законов управления порядка системы, перерегулирования, времени управления. На рисунках 2-4 приведены временные характеристики при движении платформы динамического стенда соответственно с постоянной перегрузкой, ускорением, скоростью. Движение с постоянной перегрузка реализуется заданием перемещения платформы функцией y ( t )= at ³/6. В этом случае скорость перемещения платформы динамического стенда изменяется в соответствии с функцией y 1 ( t ) = at ²/2, а ускорение платформы задается функцией y₂ ( t )= at .. Перегрузка при этом постоянна y₃ ( t )= a .

;

V + 2

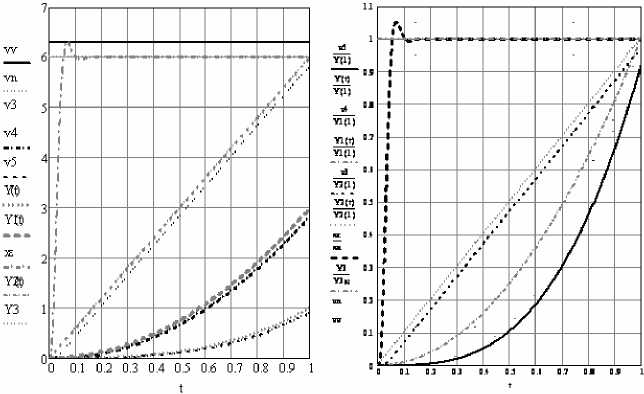
Рис. 2. Временные характеристики системы при движении с постоянной перегрузкой

Движение с постоянным ускорением реализуется заданием перемещения платформы функцией y(t)=at^/2. В этом случае скорость перемещения платформы динамического стенда изменяется в соответствии с функцией y1 (t)=at, а ускорение платформы задается функцией y2 (t)=a.

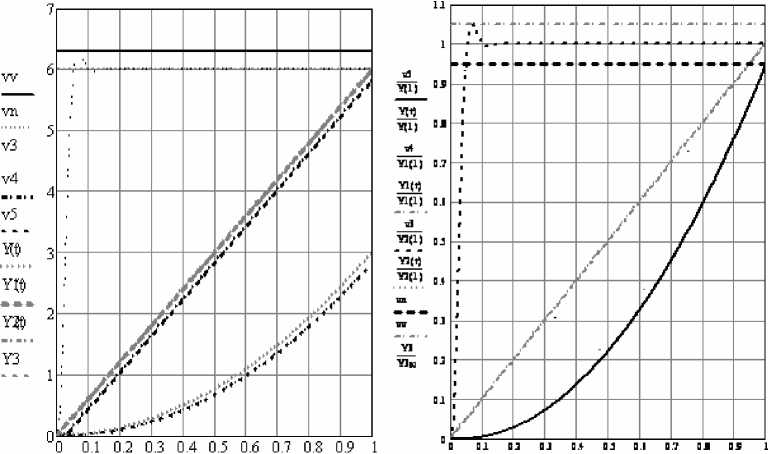
Рис. 3. Временные характеристики системы при движении с постоянным ускорением

Движение с постоянной скоростью реализуется заданием перемещения платформы функцией y(t)=at. В этом случае скорость перемещения платформы динамического стенда постоянна y1 (t)=a.

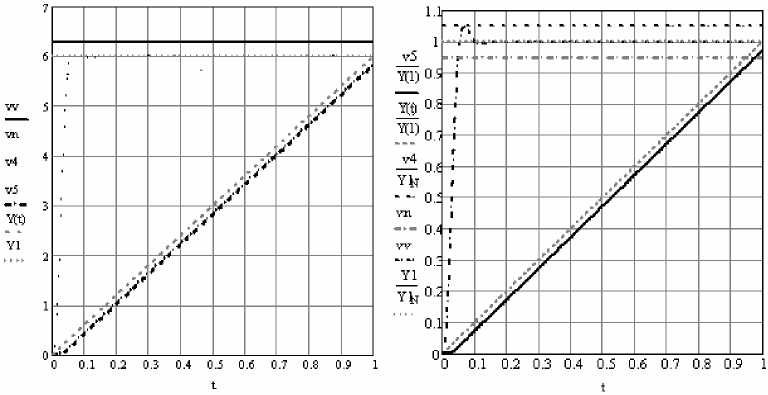
Рис. 4. Временные характеристики системы при движении с постоянной скоростью

Выводы:

• 1.    При отработке перемещений, изменяющихся по закону y ( t )= at ³/6, y ( t )= a ?/2, y ( t )= at , y ( t )= Y 0 , в системе формируется эталонная переходная характеристика соответственно: по перегрузке, ускорению, скорости, перемещению.

• 2.    Наличие в системе ненулевого времени управления приводит к одинаковому запаздыванию в отработке всех управляемых координат

• 3.    Время запаздывания в отработке управляющих воздействий не превышает 0,6 t y от времени управления при о < 5%.

• 4.    Увеличение перерегулирования в системе приводит к повышению колебательности и снижению точности в отработке законов управления: перегрузкой при задании переме-

• щения в виде y(t)=at3/6; ускорением при задании перемещения в виде y(t)=at2/2; скоростью при задании перемещения в виде y(t)=at; положением при задании перемещения в виде y(t)=Y0, но снижает время запаздывания.

• 5.    Увеличение порядка системы приводит к повышению ее колебательности и времени управления.

• 6.    Исходя из требований к тренажеру и динамическому стенду, сформированы требования к приводу динамического стенда: время управления до 0,1 с; перерегулирование σ ≤ 20%; статическая ошибка δ = 0.

(перегрузка, ускорение, скорость, перемещение) при точности их воспроизведения в астатических САУ с нулевой ошибкой.