Моделирование привода виброуплотняющего оборудования

Для моделирования привода виброуплотняющего оборудования использована программная оболочка в среде MATLAB. Эта система является идеальным средством для реализации всех видов моделирования: аналитического, численного, имитационного и ситуационного. Система имеет мощные средства диалога, графики и комплексной визуализации, а также многочисленные программные пакеты для расширения функций системы: символического дифференцирования и интегрирования, идентификации систем, построения и исследования искусственных нейронных систем, обработки сигналов и изображений, решения обыкновенных дифференциальных уравнений и т.д. Одним из таких пакетов системы MATLAB является пакет визуального имитационного и ситуационного моделирования Simulink, позволяющий исследовать многие линейные и нелинейные блочные динамические системы и устройства произвольного назначения. Модель создается из стандартных функциональных графических блоков, набор которых в пакете очень велик и постоянно расширяется. Параметры блоков задаются с помощью удобных диалоговых панелей

Гидросистема привода виброуплотняющего оборудования содержит источник питания (насос), пропорциональный распределитель, гидроцилиндр и трубопроводы (полости). Для моделирования гидропривода разработана математическая модель элементов гидросистемы. Программа гидросистемы, набранная в среде «Matlab-Simulink», приведена на рисунке 1.

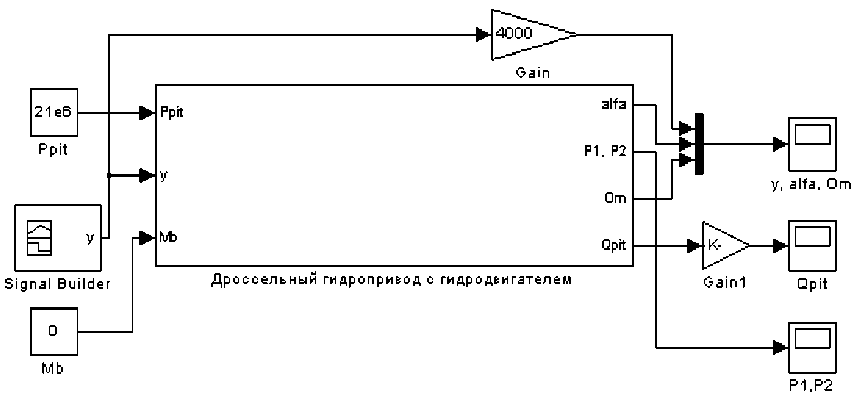
Рис. 1. Схема дроссельного гидропривода виброуплотняющего оборудования, набранная в среде «MATLAB-Simulink»

В качестве входных данных для модели использовались: постоянное давление питания (P0 = 21 МПа), внешний возмущающий момент (Mb = 0) и сигнал, соответствующий значению плунжера (ymax = 0,3 мм ), который меняется по времени и задается при помощи функции “Signal Builder” в ПК “MATLAB”.

Все постоянные значения параметров макроблоков модели гидропривода задавались при помощи “M-файла” в отдельном текстовом документе, имеющем следующий вид: коэффициент утечек в дренаж Ly, м3*с/Па; Ly=1e-11; коэффициент перетечек между полостями Lp, м3*с/Па; Lp=4e-12; модуль объемной упругости жидкости Еж, Па; Eg=9.0e8; Eg3=1e9; объем полости 1 V, м3; Wp1=0.0005; объем полости 2 V, м3; Wp2=0.0005; объем полости 3 V, м3; Wp3=1e-3; момент инерции Jgd , кг*м2; Jgd=200; коэффициент скоростного сопротивления fgd, Нм с/рад; fgd=100; максимальное давление в полостях 1,2 pmax, МПа; pmax=50e6; максимальное давление в полости 3 pmax, МПа; pmax3=25e6; минимальное давление в полости 3 pmin, МПа; pmin3=1e6; давление слива Psl, МПа; Psl=0.3e6; плотность жидкости po, кг/м3; po=800; диаметр золотника D, м; D=0.005; коэффициент использования периметра kp; kp=0.5; радиальные зазор dz, м; dz=0; коэффициент расхода u; u=0.71; gnmax=0.523; kdin=0; kreg=1e-7; kn=1.2e-3

Математическая модель насоса гидропривода разработана в соответствии со схемой, приведенной на рисунке 2, а. Блок-схема гидравлического насоса приведена на рисунке 2, б.

Работа насоса описывается уравнением моментов на валу (узел k) и уравнением потоков на входе (i) и выходе (j) с учетом объемных потерь [1].

При этом неравномерность подачи вследствие кинематических особенностей насоса и сжимаемости жидкости в полостях не учитывается.

М k = q H f ⁽ q )( P j - p ) + a — ^— + ^a _P \ p ^- - p\ + a ;

uд

Qi,j= qH f(q)—± kут p— ид где qн - максимальный рабочий объем насоса; f(q) - параметр регулирования; -1 < f(q) < 1; — - угловая скорость вала двигателя (дизеля); а— - коэффициент гидромеханических потерь, зависящих от угловой скорости; аР – коэффициент гидромеханических потерь, зависящих от давления; а – постоянная гидромеханических потерь; uд – передаточное число редуктора; kyт – коэффициент объемных потерь насоса; для Qi, pi принимается знак «плюс», для Qj, pj – «минус».

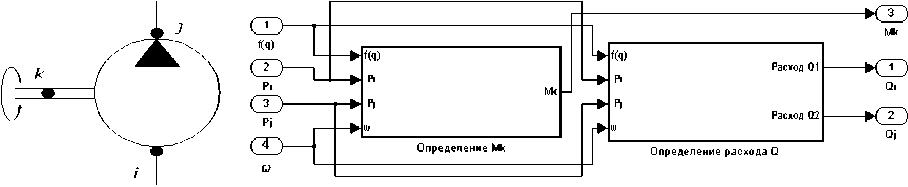
а                                             б

Рис. 2. Насос: а – расчетная схема; б – блок-схема

Моделирование насоса по параметру крутящего момента и расхода рабочей жидкости выполняется по схеме, приведенной на рисунках 3,а и 3,б.

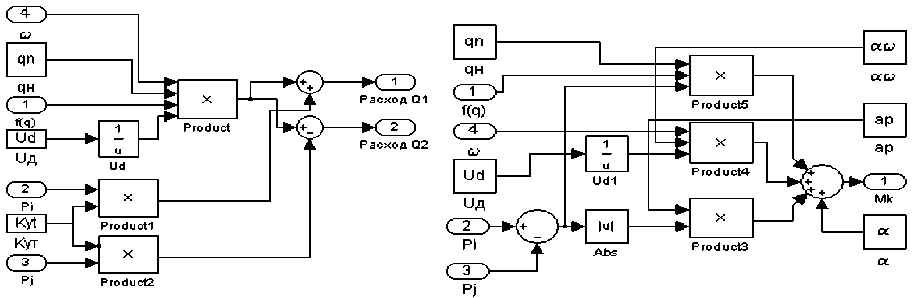
а

б

Рис. 3. Макроблок: а – определения крутящего момента; б – определения расхода рабочей жидкости (Qi иQj)

Динамика гидроцилиндра, расчетная схема которого приведена на рисунке 4,а, описывается уравнениями поступательного движения поршня (узел k) под действием сил давления, внешней нагрузки, сил трения и уравнениями расходов на входе (i) и выходе (j) с учетом сжимаемости жидкости в полостях. На рисунке 4,б приведена блок-схема гидроцилиндра, содержащая макроблоки по моделированию расхода рабочей жидкости (Q), коэффициента упругости рабочей жидкости (Kупр), скорости выдвижения штока гидроцилиндра (Vk), усилия (F), приведенного объемного модуля упругости полости с жидкостью (Епр), коэффициентов пропорциональности между давлениями в полостях I (i) и II(j) и силой трения в манжетных уплотнениях (К).

► Расход Qi Расход Qi

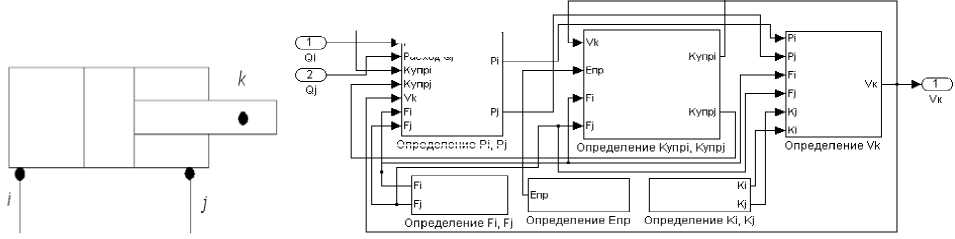
Определение Pi, Pi

б

а

Рис. 4. Гидроцилиндр: а – расчетная схема; б – блок-схема иk = m-1 [pF - PjFj - hu - (RTp + kpi + kjPj)signUk - RЦ ] ;

.                            Q, - Fpk           FU - Qj zk = u ,0 < zk < L ; Pi =       ; Pj = -^r-1-;

kkц          упрi            упрj k,, = П f (D + Dj H;k„,

Eпр где U - скорость поршня; т - приведенная

А V + z_kF_t

Eпр

E ж

1 + D ^Еж

S Е ст

;

упрj

A V + ( L - _{Z k} ) j

E ; пр

к штоку масса подвижных частей гидроцилиндра;

Fi = п(D -Di2)/4 рабочая площадь поршня в полости I, примыкающей к узлу i (здесь D4 - диаметр цилиндра; Di - диаметр штока в полости I); Fj = п(D - Dj)/4 - рабочая площадь поршня в полости II, примыкающей к узлу j (здесь Dj - диаметр штока в полости II); h - коэффициент вязкого трения; R^р - сила трения в манжетных уплотнениях при отсутствии давления; Rц – усилие на штоке; Lц – ход поршня; f – коэффициент трения уплотнения по поверхности цилиндра; H - высота манжетного уплотнения; А Vi и A Vj - мертвые объемы полостей I и II; Eпр – приведенный объемный модуль упругости полости с жидкостью; Еж – объемный модуль упругости рабочей жидкости; S - толщина стенки цилиндра; Ест - модуль упругости материала стенки цилиндра.

Макроблок “ Золотник ” реализует математическую модель дросселирующего распределителя на примере четырехщелевого цилиндрического золотника при произвольной гидравлической нагрузке. Расчетная схема золотника приведена на рисунке 5,а. На рис. 5, б – блок-схема золотника. Расход через местное сопротивление золотника выражается зависимостью

Р f_rs ⁽ z ) sign ⁽ P r ^- P_s )

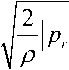
^- P s | - ^Q,

Qrs = B где frs (z) - площадь проходного сечения канала золотника, соединяющего узлы на входе (i) и выходе (j), в функции перемещения золотника z, максимальное значение которой равно nDy2 / 4 (здесь Dy-условный проход).

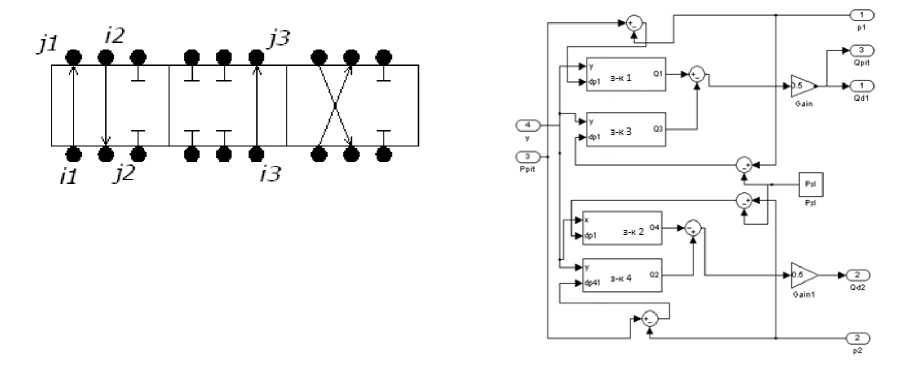
б

а

Рис. 5. Золотник: а – расчетная схема; б – блок-схема

Учтены рекуперативные динамические режимы при произвольном давлении питания. Скорость движения золотника регулируется сигналом управления его распределителем. При таком управлении изменяется продолжительность пребывания распределителя в крайнем положении, что позволяет уменьшать или увеличивать среднюю скорость движения выходного звена. Однако дискретное переключение распределителя обычно сопровождается колебаниями давлений в напорной и сливной магистралях, а также в каналах аппарата управления и полостях исполнительного двигателя, что может вызвать повреждение элементов привода.

Гидроприводы большинства мобильных машин характеризуются сравнительно малой длиной простых участков трубопроводов, редко достигающей 5 м, и относительно невысоким быстродействием направляющей гидроаппаратуры. Рабочее давление достигает 20 МПа, а в отдельных случаях 30 МПа. В этих условиях, как показывают специальные исследования, для описания динамических процессов в трубопроводах с жидкостью допустима математическая модель с сосредоточенными параметрами на входе (i) и выходе (j).

Расчетная схема трубопровода приведена на рисунке 6,а. Блок-схема трубопровода приведена на рисунке 6,б.

а

Pi =

Q Q ;

k упр . тр

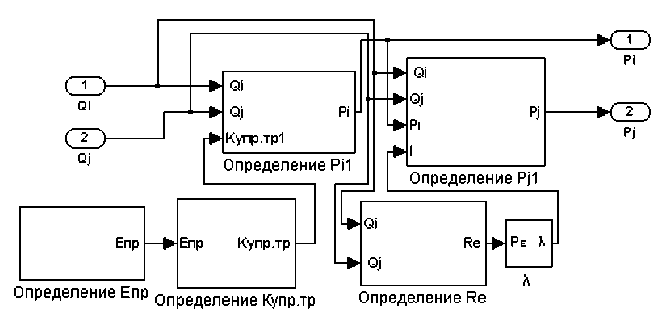
б

Рис. 6. Трубопровод: а – расчетная схема; б – блок схема

P j = Pi ~ A

8 p L_m p n ² d⁵ тр

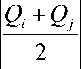
E          f 75/Re

L =---—---; A = ^

пр 1 + d тр Еж      [0.31464Re д E тр ст

Q + Q        nd2 L ij         тр тр

2    ; k упр. тр = 4 E     ’ пр при Re < 2300 r = 2|Q + Qj\ при Re > 2300 ’       пdтрVЖ

где k _{упр . тр} – коэффициент упругости трубопровода с жидкостью; d_тр – диаметр трубопровода; L_тр – длина трубопровода; E_пр – приведенный объемный модуль упругости трубопровода с жидкостью; E _ж – модуль упругости жидкости; д _тр - толщина стенки трубопровода; Е _ст - модуль упругости материала трубопровода; A - коэффициент потерь по длине; Re-число Рейнольдса, v _x - кинематическая вязкость жидкости; р - плотность рабочей жидкости.

Блок-схема трубопровода содержит пять макроблоков по определению плотности рабочей жидкости, приведенного объемного модуля упругости трубопровода с жидкостью, коэффициента упругости трубопровода с жидкостью, числа Рейнольдса, коэффициента потерь по длине трубопровода.

Рассмотренные уравнения справедливы при следующих условиях:

• -    волновые процессы в трубопроводах не рассматриваются;

• -    потери давления по длине трубопровода зависят от среднего значения расходов на входе и выходе;

• -    инерционная составляющая сил рабочей жидкости в трубопроводах не учитывается.`

В результате моделирования работы гидропривода в течение четырех секунд с использованием блоков “Scope”, выполняющих функции осциллографов, были получены графические результаты зависимостей параметров гидросистемы виброуплотняющего оборудования (рис. 7, 8).

Давление в гидролиниях достигает максимума за две секунды и составляет 17 МПа.

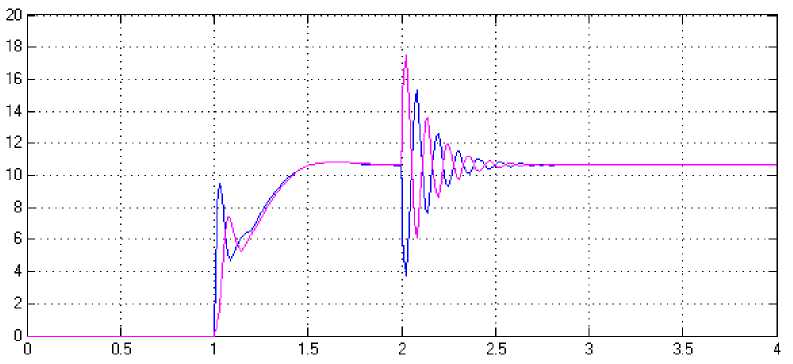
Рис. 7. Давление в гидролиниях, МПа

Сводный график зависимостей угловой скорости, угла поворота, смещения плунжера и давления питания от времени работы гидропривода приведен ниже на рисунке 8. Как видно из рисунка, пропорционально давлению в системе происходит изменение угловой скорости, угла поворота и смещения плунжера. Переходный процесс дросселирования рабочей жидкости в начальный период времени работы гидроцилиндра является колебательным. Через 2,5 с процесс становится стационарным. Переходная характеристика вызвана скачком градиента при турбулентном течении рабочей жидкости. При изменении разности давления на клапане процесс дросселирования неустойчив в течение 2,5 с. Далее процесс становится стационарным.

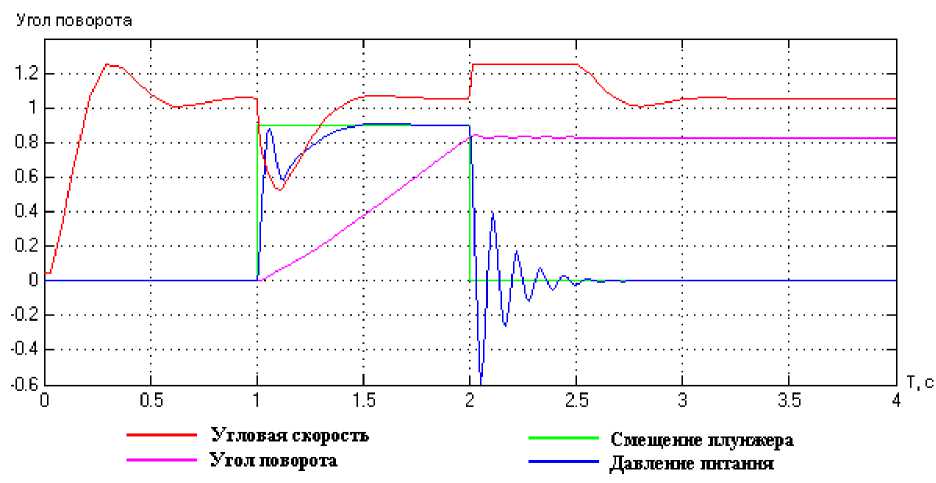
Рис. 8. Угловая скорость (рад/с), угол поворота (рад), смещение плунжера, давление питания

Выводы. Разработка программы в среде «MATLAB-Simulink» позволяет определять основные характеристики и обеспечивает устойчивую работу привода виброуплотняющего оборудования.