Моделирование процесса деформирования керамики в режиме сверхпластичности

Целью работы является разработка математической модели горячего прессования керамических заготовок в режиме сверхпластичности, позволяющей осуществлять обоснование рациональных технологических параметров процесса. При построении модели важную роль играет выбор определяющих соотношений, адекватно описывающих поведение материала при деформировании. В работе описаны основные физические механизмы, происходящие при сверхпластическом деформировании керамики, приведены вывод и обоснование определяющих соотношений.

Отдельный раздел посвящен проблеме пластического деформирования керамики, проявляющей эффект памяти формы (ЭПФ). Такой механизм неупругой деформации присутствует в частично стабилизированной керамике на основе двуокиси циркония (ZrOff что позволяет использовать эту керамику в технике, т.к. она обладает значительной трещиностойкостью. В настоящее время создано множество математических моделей деформирования такого рода материала. Одним общим недостатком этих моделей является то, что они неудобны при решении краевых задач механики деформируемого твердого тела. Как правило, с помощью построенных математических моделей, преодолевая значительные вычислительные трудности, решают задачу деформирования представительного объема. Поэтому существует необходимость создания определяющих соотношений, пригодных для решения краевых задач методами механики сплошных сред.

Вывод и теоретическое обоснование определяющих соотношений деформирования керамики в режиме сверхпластичности

Под сверхпластичностью понимают такое состояние материалов, при котором существенно возрастает их способность деформироваться без признаков макроскопического разрушения с одновременным уменьшением напряжения течения. В настоящее время установлено, что эффект сверхпластичности проявляется на всех машиностроительных сплавах на основе железа, никеля, титана и др. [1]. В 1985 г. явление сверхпластичности было обнаружено в некоторых окислах , а именно - в тетрагональных поликристаллах диоксида циркония, стабилизированных УэО^ [2]. Было сделано заключение, что сверхпластичность - это один из видов деформации мелкозернистых поликристаллических твердых тел, включающих в себя металлы, ионные и ковалентные поликристаллы при повышенных температурах.

Экспериментально установлено [3], что в сверхпластическом состоянии действуют следующие механизмы деформации: зернограничное проскальзывание (ЗГП), внутризеренное дислокационное скольжение (ВДС), диффузионная ползучесть (ДП). Данные механизмы характерны и для обычной деформации, уникальность явления сверхпластичности определяется качественно новым их взаимодействием.

В работе [2] приводятся результаты изучения микроструктурных изменений в процессе сверхпластической деформации ZrCh, стабилизированного Y2O3. Отмечается, что доминирующим механизмом деформации является ЗГП. вклад которого в суммарную деформацию оценивается в 70-80%. Аккомодационными механизмами являются ВДС и ДП, причем первый преобладает в крупнозернистых материалах при высоких напряжениях, тогда как в мелкозернистых материалах при низких напряжениях наблюдается в основном диффузионная ползучесть.

Отмечается [2], что важным элементом микроструктурного состояния сверхпластичных материалов является зернограничная пористость. В работах [4,5] высказывается мысль о том, что зернограничные поры могут обеспечивать легкое ЗГП - главный деформационный процесс сверхпластического течения. Авторы [4.5] отмечают, что присутствие зернограничных пор снимает необходимость полной аккомодации, призванной обеспечить сплошность материала. В работе [1] проведен термодинамический анализ указанного явления. Показано, что при свехпластичности дополнительное раскрытие пор при ЗГП вызывает обратную термодинамическую реакцию в материале - стремление уменьшить объёмное содержание пор. Таким образом поддерживается постоянный уровень пористости в ходе динамического процесса зарождения одних и “схлапывания” других пор при ЗГП.

В то же время, согласно [3], наличие зернограничных пор не означает отсутствия необходимости в аккомодации ЗГП. Автор [3] полагает, что процесс сверхпластической деформации должен начаться с генерации зернограничных дислокаций. Поверхности границы не всегда плоские, на них имеются тройные стыки, пороги, что является препятствием для движения ЗГД. Для дальнейшего развития деформации путем движения ЗГД необходим аккомодационный механизм, который обеспечивал бы “рассасывание” ЗГД в скоплениях.

Наиболее эффективным процессом аккомодации может служить зарождение решеточных дислокаций (РД. Генерированные на границах зерен дислокации решетки проходят через зерна и поглощаются границей. В работе [6] предполагается, что под воздействием бомбардировки РД границы зерен в определенных температурно-скоростных условиях нагружения могут переходить в особое аморфное состояние с низким сопротивлением ЗГП. Переход границы в такое состояние осуществляется в результате перестройки ее атомной структуры . приводящей к делокализации ядра попавшей в границу РД. В то же время движение РД связано с зарождением и поглощением вакансий, поэтому вследствие разной плотности и подвижности ЗГД на различных границах зерен возникают локальные диффузионные потоки - развивается диффузионная аккомодация.

Заметим, что из результатов исследований, проведенных авторами [2] и [3], следует, что вышесказанное справедливо как для металлических, так и для керамических материалов.

Выведем соотношения, описывающие закономерности сверхпластической деформации. Большинство авторов, ставя перед собой подобную задачу, рассматривают простые напряженные состояния, когда существует только одна компонента тензора напряжений (деформаций, скоростей деформаций), очевидно, равная интенсивности [2,3,7,8,9]. В дальнейшем делается попытка обобщить полученные соотношения для сложного напряженного состояния. Данный подход используется и в настоящей работе.

Величина пластической деформации при свехпластичности обусловлена вкладами трех механизмов:

ер ~ £Л I! +еВДС 5ДП ’ где ер - интенсивность пластической деформации.

Отсюда имеем sp — ^Л И + ^ВДС + 5ДИ •                                                        (О

В оптимальных условиях сверхпластичности вклады ВДС ^ДП незначительны, поэтому

° ЗГП*

Согласно уравнению Орована [3]:

8р =8.ип =КЬр5 ,                                                (2)

где Ь, Э,р - усредненные модуль вектора Бюргерса, скорость движения и объёмная плотность ЗГД; К - коэффициент усреднения. Плотность зернограничных дислокаций определяется уравнением dp/dt - р' - р/т ,                                                               (3)

где р+(о) - скорость увеличения плотности ЗГД; т - среднее время жизни ЗГД. которое определяется расстоянием, на которое перемещается дислокация и скоростью ее движения (расстояние примерно равно диаметру зерна X ), т.е. т дХ/d .Величину р+ можно оценить из соотношения р+ £X(5n/5t) .                                                                (4)

где X - размер зерна; £ - объёмная плотность источников ЗГД ( 5,д1/х³): 5n/5t -скорость зарождения ЗГД.

Для вычисления 5n/5t воспользуемся обобщенной силовой моделью дислокационного источника [10], в соответствии с которой источник зарождает дислокации, пока эффективные напряжения на источнике превышают некоторое критическое значение:

где аоб - обратные напряжения от уже испущенных дислокаций.

Так как за время 5t испущенные бп дислокации переместятся на расстояние 5L-96t, то источник будет непрерывно испускать дислокации, пока оо6 от бп дислокаций (соб - Gb6n/6tT [9]) будут меньше или равны о - о, :

5n/5t = 9(ст -Oj)h(a -щ -no6)/Gb ,(5)

где Н(с> - сд - а05) - функция Хевисайда.

Подставив уравнения (5) и (4) в (3), получим dp/dt + p/т = (а - Oj)h(c - щ -аоб)9/ОЬХ2 .

На стадии стабильной деформации о = const и последнее уравнение имеет решение: p(t) = (а-О;)Ь(а-щ - oo6)/GbX + ро ехр(—t/т) ,(6)

где р₀ - начальная плотность ЗГД.

Из уравнения (6) следует, что при t > т плотность ЗГД стремится к постоянному значению:

р,       Oi)h(a-o-i -CTo6)/GbX .(7)

Для определения скорости движения ЗГД воспользуемся выражением [9]:

Т = цЕ(о-oj/ldkTX ,(8)

где ц - коэффициент зернограничной диффузии; Е - вакансионный объём.

Из выражений (2), (7) и (8) для стадии стабильного течения получаем соотношение sr цЕ(п o,)2/l6GkTX2 .(9)

Из соотношения (9) можно вычислить величину коэффициента скоростной чувствительности напряжения течения т:

т = clgo/dlgs = (о-С|)/2о .(10)

Из выражения (10) следует, что при а >>0, коэффициент m -э 0.5, что и наблюдается обычно в условиях сверхпластической деформации.

Уравнение (9) хорошо согласуется с экспериментальными данными для оптимальных скоростей сверхпластической деформации керамических материалов.

Моделирование процесса деформирования керамики с учетом фазовых превращений

Рассматриваемые в первом разделе определяющие соотношения во многих случаях с достаточной для практики точностью описывают процессы сверхпластического деформирования для широкого круга материалов. Однако для ряда материалов и процессов их переработки существенными являются другие механизмы деформирования, отличные от ЗГП, ВДС, ДП.

Одним из наиболее эффективных процессов аккомодации при сверхпластическом деформировании ZrO2, стабилизированного ^2^3- могу г служить фазовые превращения кристаллической решетки циркония. В рамках построения определяющих соотношений с учетом этих превращений перейдем к выводу энергетического критерия фазового превращения в керамике при сложном напряженно-деформированном состоянии.

Большинство известных математических моделей трансформационной пластичности используют уравнение Клаузиуса-Клапейрона для нахождения эффективной температуры превращения Т , обеспечивающей инвариантность температуры мартенситного превращения Тт относительно приложенного напряжения:

Т* ^t-^D- a . Q

(И)

где Q - тепловой эффект превращения;

D    - дисторсия превращения;

СУ     - скорость изменения внешних напряжений.

При этом классическое уравнение Клаузиуса-Клапейрона впервые было получено не для твердотельных превращений, а для превращений типа жидкость-твердое тело и т.п. Затем уравнение было модифицировано и приобрело вид (11). С тех пор уравнение широко применяется для твердотельных превращений. С помощью уравнения (II) можно найти эффективную температуру Т¥ для элеменгарного объема материала. Недостатком этого подхода можно считать невозможность учета взаимодействия выбранного элементарного объема с окружающей его матрицей. Многие математические модели пренебрегают такого рода взаимодействием, считая дисторсию превращения наперед заданной величиной. При этом не рассматривается один из важнейших вопросов механики сплошных сред - вопрос совместности деформаций.

Поэтому возникает необходимость в рамках построения определяющих соотношений получить уравнение для эффективной температуры при твердотельных превращениях объектов типа "включения в матрице" и сравнить полученный результат с уравнением (1 1). Вводятся следующие гипотезы:

• 1.    Рассматривается материал, обладающий свойством полиморфизма и имеющий только две (а и b ) фазы.

• 2.    В качестве термодинамического потенциала, характеризующего структуру кристаллической решетки, выбирается свободная энергия F=U-TS. При этом предполагается, что кристаллическая решетка является консервативной системой (здесь S - энтропия системы, U - внутренняя энергия ).

• 3.    Предполагается, что а - фаза данного материала устойчива при низких температурах при отсутствии внешних напряжений, b - фаза этого же материала, напротив, устойчива при высоких температурах, так что существует температура Т_т , при которой F_a⁼Fb- Такая температура называется температурой мартенситного превращения или точкой равновесия фаз.

• 4.    Предполагается, что процесс перехода менее стабильной фазы в более стабильную (фазовый переход I рода, трансформация) совершается настолько медленно, что в каждый момент времени в данной точке тела успевает установиться состояние термодинамического равновесия, соответствующее внешним условиям, в которых тело в данный момент находится. Тогда процесс будем считать термодинамически обратимым.

• 5.    Будем предполагать, что внутренняя энергия U и энтропия S а и b фазы одинаково изменяются с изменением температуры, поэтому их разности не зависят от температуры:

• 6.    Будем считать, что процесс трансформации происходит при постоянной

ат 'ат ’

где AU = Ua-Up, AS = SH-Sp

температуре.

Перейдем к формулировке энергетического критерия мартенситного превращения.

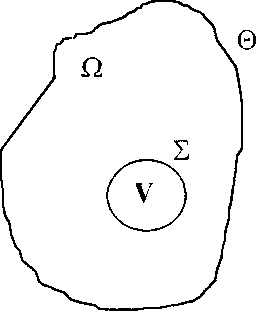
Рис. 1. Включение Ь- фазы в «-матрице

Рассмотрим включение /)-фазы объема V. ограниченное поверхностью Е, в (/-матрице (рис.1). Включение трансформируется, изменяя свой размер и форму; при этом над включением совершается работа dA. Граница X между включением и матрицей считается когерентной, а деформация в матрице и включении -упругой. Используя гипотезу 4. запишем основное уравнение термодинамики для равновесных процессов:

d(AU) = Td(AS) + dA                       (12)

Так как процесс трансформации считается изотермическим (гипотеза 6), то из (12) следует dF = dA.

Рассмотрим трансформацию аналогичного объема V при отсутствии внешних (относительно включения) сил, т.е. dA=0. При таких внешних условиях трансформация может произойти только в точке равновесия фаз Т т:

d(AU)-Tmd(AS) = О,

d(AS) = ^M                                           (14)

т

Воспользуемся гипотезой 5 и перепишем уравнение (12):

dA=d(AU)-                                                    (15)

Последнее уравнение можно назвать уравнением равновесия фаз. Нужно отметить, что уравнение (15) весьма похоже на уравнение Клаузиуса-Клапейрона, с той лишь разницей, что под работой в последнем уравнении понимается работа, совершаемая над включением объема V , а в уравнении (11) под D- а понимается работа, совершаемая над элементарным объемом материала. После получения dA из (15) возникает возможность описания трансформационной пластичности на мезоуровне, т. е. на уровне матрицы и включения.

При определении dA будем учитывать, что матрица и включение оказывают влияние друг на друга. Найдем dA как разность упругих энергий матрицы до и после превращения, исключая работу внешних сил на несвязанных с превращением деформациях dA = dW-dWc.

Представим исходную задачу суперпозицией двух задач (рис. 2), предполагая аддитивность напряжений и деформаций.

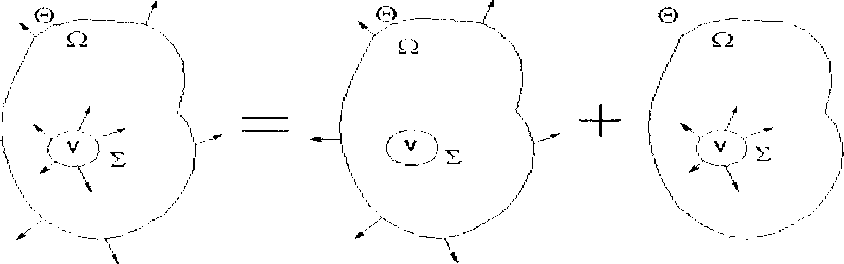
Рис.2. Суперпозиция двух задач

За счет того, что включение изменяет свою форму и размер, оно начинает действовать на окружающую его матрицу. Это действие можно заменить силами, распределенными по поверхности включения. Будем считать, что напряжения, возникающие в матрице являются упругими, поэтому о' = а° +о ,

Изменение упругой энергии в задаче (см. рис.2,а)

dW - J|Jd'• de Mv-JJJ|^d -de+ 25° ■ de + су °-de⁰ jdv ,                      (16)

Q                 12

где Q - объем матрицы.

При выводе уравнения (16) использована теорема Бетти для двух различных напряженных состояний (см. рис.2,б,в).

Первый член в правой части уравнения (16) представляет собой работу dWc внешних сил в задаче (см. рис.2,6):

dWe - UJo - dedv .(17)

Последний член в правой части (16) представляет из себя работу dW1, которая совершается над включением, при изменении его размеров и формы, при отсутствии внешних нагрузок (рис. 2,в). Переходя к интегрированию по поверхности, получим dW1 = jjj^°'    dv = J J t ° • du* ds + jj t° -du* ds ,(18)

sr                es где t° - силы на границе 0, вызванные присутствием включения;

• t °     - вектор сил на поверхности включения У в задаче рис.2,в;

dll* - смещение границы Е в результате превращения.

Учтем граничные условия на 0 ( t ’ = б) , тогда уравнение (18) будет иметь вид dW1 = JJjo° -de0 dv = Jjt° du° ds .                                       (19)

Аналогичным образом преобразуем второй член в правой части уравнения (16) dW'c = 2|ДсС -de = 2|Да-с1С = 2 Д t* du°ds,                         (20)

Q где t* - вектор сил на поверхности X в задаче рис.2,6.

Используя (16), (17), (19) и (20), перепишем уравнение равновесия фаз

dW‘ + dW,e = Д(С + 2U) ■ du: ds = d(AU) 1 -

Определим правую часть уравнения (21). Пусть qa , ra - удельная внутренняя энергия и плотность материала матрицы, a q^ , г^ - удельная внутренняя энергия и плотность материала включения, соответственно. Следовательно, изменение внутренней энергии включения в результате превращения

d(AU) = dVpqp 4 dVaqa .

Принимая во внимание то, что dma = -dnip, получим

d(AU)=dVp qp-

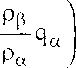
Перепишем (22) в более простом виде, учтя обозначения dV = dVp, q =qp - — q(, , Pp d(AU) = dVq .                                                       (23)

В самом общем случае q - функция напряжений и температуры, т.к и плотности, и удельные внутренние энергии обеих фаз зависят от НДС и температуры. Таким образом, окончательный вид уравнения (1 5) с учетом (23):

dW1 + dWlc

-q 1--— dV .

Используя уравнение (24), эффективную температуру можно определить выражением

Т* - Тт---dW1 +dW'e .                                         (25)

q dV

Анализ полученных результатов

Из уравнений, полученных ранее, не совсем понятна роль ориентационного фактора внешней нагрузки, хотя очевидно, что эволюция включения сильно зависит от вида внешнего нагружения. Запишем уравнение (25) в развернутом виде

• Т* = Т_т - -^ Д(t: + 2tД • da: ds.

Проанализируем последнее уравнение для dV>0 при различных видах внешней нагрузки. Понятно, что наименьшей эффективной температуры можно добиться при условии коллинеарности векторов С°4-2и и du: на границе включения. Например.

для сферического включения с радиальным вектором du° минимальная температура Т* реализуется при всестороннем растяжении.

В качестве тестовой задачи рассматривалось круглое включение в матрице под действием растягивающих, сжимающих, а также сдвиговых усилий Р, приложенных на бесконечности (рис. 3), при различных коэффициентах объемного расширения трансформирующегося материала g.

Рис. 3. Тестовая задача

Полученные результаты представлены на рис. 4 в виде зависимостей эффективной температуры от коэффициента объемного расширения g.

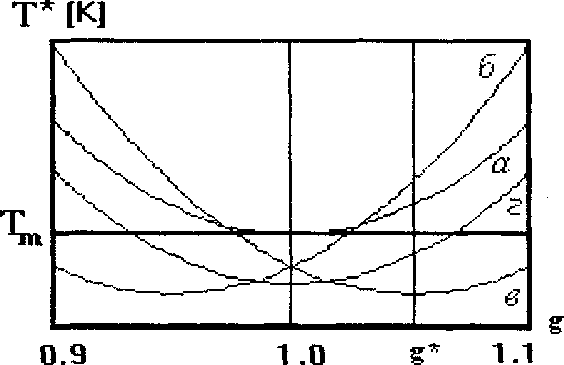
Рис. 4. Зависимости эффективной температуры от коэффициента объемного расширения g:

а) напряжения отсутствуют Оу =0; б) сжимающие напряжения Ст] ]<0;

в) растягивающие напряжения О] ]>0; г) сдвиговые напряжения О] э^-

Как видно из полученных результатов, эффективная температура зависит от интенсивности, а также от вида нагружения. Для материала с коэффициентом объемного расширения g =1.057 , при вариантах нагружения "а" - "г", минимальная эффективная температура реализуется при одноосном растяжении, хотя и при простом сдвиге она ниже температуры Тт.