Моделирование процесса деформирования пластины с концентратором напряжений при учете закритической стадии деформирования материала
Автор: Вильдеман В.Э., Третьяков М.П., Мугатаров А.И.
Статья в выпуске: 3, 2020 года.
Бесплатный доступ
Закритическое деформирование материала - это процесс, характеризующийся снижением напряжений при растущих деформациях в результате накопления структурных повреждений. Конструкция становится неспособной выдерживать внешние воздействия только в том случае, когда зоны разупрочнения достаточно развиты. Развитие зон закритического деформирования материала может происходить при увеличении внешней нагрузки, прикладываемой к конструкции. Из этого следует, что учет разупрочнения материала при деформировании позволяет более точно определить прочностные и деформационные резервы конструкций. В работе приведена математическая постановка краевой задачи механики закритического деформирования. Перечислены особенности экспериментального изучения закритической стадии деформирования материала. Получены диаграммы деформирования различных сталей с протяженным участком разупрочнения, а также численные решения для задач деформирования тонкой пластины с концентраторами напряжений различной геометрии при кинематическом нагружении. Рассмотрены двухзвенная и трехзвенная аппроксимации диаграммы деформирования материала, а также реальные диаграммы деформирования стали 20 и стали 40Х, полученные экспериментально. Проанализирована эволюция зон закритического деформирования в материале. Определено соответствие между значением модуля спада и характером эволюции зон разупрочнения. Построена эпюра напряжений, отражающая, каким образом реализуется полная диаграмма деформирования материала вблизи концентратора. Построены расчетные диаграммы нагружения. Отмечено, что даже после появления зон разупрочнения возможен рост внешней нагрузки. Определены прочностные и деформационные ресурсы конструкций, рассмотрено влияние геометрии концентратора напряжений на их значения. Отмечено, что учет разупрочнения при моделировании поведения конструкций с концентраторами напряжений является целесообразным.
Закритическое деформирование, разупрочнение, математическое моделирование
Короткий адрес: https://sciup.org/146282002
IDR: 146282002 | УДК: 539.3 | DOI: 10.15593/perm.mech/2020.3.04
Текст научной статьи Моделирование процесса деформирования пластины с концентратором напряжений при учете закритической стадии деформирования материала
ВЕСТНИК ПНИПУ. МЕХАНИКА № 3, 2020PNRPU MECHANICS BULLETIN
Закритическая стадия деформирования материала характеризуется снижением уровня напряжений при растущих деформациях [1-8]. Процесс накопления повреждений в материале с развитием зон разупрочнения может быть устойчивым при достаточной жесткости нагружающей системы [9, 10]. Основные теоретические положения механики закритического деформирования представлены в [11, 12]. Экспериментально полная диаграмма деформирования материала может быть получена с использованием испытательных машин с высокой жесткостью [13-20]. В работе [21] получены опытные данные о закритическом поведении конструкционных сталей при различных видах напряженно-деформированного состояния, в частности в опытах на кручение и совместное растяжение с кручением образцов. Изучено влияние различных факторов на степень реализации стадии разупрочнения. Рассмотрено влияние повышенной температуры на проявление закритического поведения сталей [19, 21]. Исследовано влияние предварительной закрити-ческой деформации на процессы ползучести и релаксации при высоких температурах. Показано положительное влияние дополнительных вибрационных воздействий на устойчивость процессов закритического деформирования. Аналитические решения задач с учетом полной диаграммы деформирования материала получены в работах
В.А. Ибрагимова, В.Д. Клюшникова, Л.В. Никитина, Е.И. Рыжака, С.Д. Волкова, Г.И. Дубровиной, Ю.П. Со-ковнина, В.В. Стружанова, В.Э. Вильдемана [11, 22-26]. Численные решения краевых задач механики закритиче-ского деформирования получены в работах В.П. Радченко, С.В. Горбунова, В.Э. Вильдемана и других авторов [27-30].
1. Математическая постановка краевой задачи механики закритического деформирования
Краевая задача механики закритического деформирования [11-12, 21] (без учета массовых сил) представляет собой систему из 15 дифференциальных уравнений:
' a, j (r ) = °;
' £kl ( r )= 2 (uk,l ( r ) + ul,k ( r ) + um,k ( r ) um,l ( r )) ; (1)
_ Oj (r ) = Cijkl (r )(Iklmn -^klmn ( r ))£mn (r ) , где r - радиус-вектор; aj (r) - тензор напряжений; £kl (r) - тензор конечных деформаций; ui ( r) - вектор перемещений; Cjjkl (r) - тензор упругих свойств; Iklmn = (5 km 8 ln +8 kn 8 m) /2; 5 km - дельта-символ Кронеке- ра; Qklmn (r) - тензор поврежденности четвертого ранга. В случае изотропного материала физические соотношения можно записать в виде
^■(ej = 3 G (1 — ®(б))б-;
О , — ^ ((^п О 22 )+ ( ° 11 О 33 ) + ( ° 22 О 33 ) + 6 (т 12 + Т 13 + Т 23 )
S i — 3 (jt6" S 22 ) + (б 11 S 33 ) + (б 22 S 33 ) + 2 (7 12 +7 13 +Y 23 ) , (2)
где го ( е eq ) - скалярная функция поврежденности [31]; o i - интенсивность напряжений; s i - интенсивность деформаций; G – модуль сдвига. Данные уравнения дополняются граничными условиями контактного типа, которые учитывают жесткость (либо податливость) нагружающей системы:
(o n + Rijuj )|Ss — S0, (ui+ Qij Оjknk )|2u — u0, где Rij – коэффициенты жесткости нагружающей системы; Qij – коэффициенты податливости нагружающей системы; ni – направляющие косинусы вектора нормали к поверхности тела в данной точке; ui0 – перемещения, номинально заданные на границе Su; S, - силы, номинально заданные на границе SS . При бесконечно большой жесткости нагружающей системы данные граничные условия вырождаются в граничные условия в перемещениях, при бесконечно малой – в напряжениях.
Все решения, приведенные ниже, получены в стандартном вычислительном комплексе Abaqus CAE. Рассмотрены модели материалов с изотропным упрочнением и упругой разгрузкой. Полные диаграммы деформирования задавались в виде таблицы зависимости эквивалентных напряжений по Мизесу от эквивалентных пластических деформаций; промежуточные значения получаются интерполированием точек.
-
2. Особенности экспериментального изучения закритической стадии деформирования
Для экспериментального изучения закономерностей закритического деформирования материалов применяются испытательные машины, предназначенные для работы в режиме кинематического нагружения и характеризующиеся высокой жесткостью. Это требуется для реализации контролируемой скорости деформирования материала на стадии разупрочнения и обеспечения высокой жесткости нагружающей системы по отношению к испытываемому образцу. С той же целью используются образцы с малой длиной рабочей части.
Были проведены испытания образцов различных конструкционных сталей на растяжение, в результате которых получены диаграммы деформирования с развитыми участками закритического поведения. На рис. 1 приведены диаграммы деформирования для сталей: 1 – 15Х2ГМФ, 2 – 40Х, 3 – 45, 4 – 25, 5 – Ст3, 6 – 20. Испытания проводились на универсальной двухосевой серво-гидравлической испытательной системе Instron 8850, обладающей высокой жесткостью [21]. Данные на рис. 1 приведены в осях инженерных напряжений и инженерных деформаций, полученных путем отношения нагрузки и перемещений к начальной площади поперечного сечения и начальной длине рабочей части образца соответственно. Учет возниконовения локализации деформаций в виде «шейки» при интерпретации результатов испытаний в условиях реализации стадии закритического поведения является самостоятельным направлением расчетно-экспериментальных исследований и испытаний при совместном использовании машины и видеосистемы регистрации полей перемещений и деформаций, основанной на методе корреляции цифровых изображений.
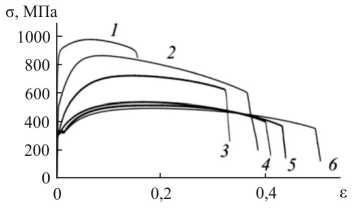
Рис. 1. Диаграммы деформирования сталей: 1 – 15Х2ГМФ; 2 – 40Х; 3 – 45; 4 – 25; 5 – Ст3, 6 – 20
Fig. 1. Strain curves of steels: 1 – 15CrMoV4, 2 – 40Cr4, 3 – C45E, 4 – C25E, 5 – A3, 6 – 20
Из рис. 1 видно, что закритическая стадия деформирования, начало которой соответствует достижению максимальных напряжений, является более протяженной по сравнению со стадией упругопластического деформирования. Очевидно, что учет этой стадии в расчетах должен обнаружить деформационный резерв элементов конструкций.
Для дальнейших расчетов будет использована диаграмма 2 на рис. 1, полученная при испытании образца из стали 40Х.
-
3. Моделирование процесса деформирования пластины с концентратором напряжений для двухзвенной и трехзвенной диаграммы деформирования
Рассмотрим моделирование процесса разрушения тонкой пластины с круглым концентратором при растяжении. Геометрия образца: ширина и длина пластины 100 мм, диаметр центрального отверстия 10 мм; к верхней грани приложено перемещение 0,1 мм за условную единицу времени, нижняя грань закреплена шарнирно.
Принято, что пластина состоит из однородного материала, модуль Юнга Е = 200 ГПа, коэффициент Пуассона ν = 0,3, предел текучести σ т = 200 МПа. Были рассмотрены следующие модели: упругопластическая с линейным упрочнением, модули упрочнения E ' = 100 ГПа, 25 ГПа; идеальная упругопластическая модель; упругопластическая с линейным разупрочнением, модули спада D = 5 ГПа, 10 ГПа. Диаграммы деформирования приведены на рис. 2.
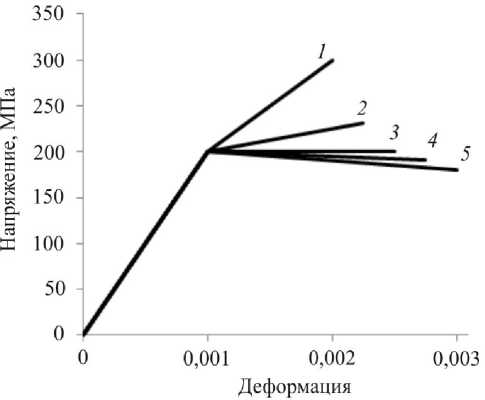
Рис. 2. Диаграммы деформирования: 1 – E ′ = 100 ГПа;
2 – E ′ = 25 ГПа; 3 – E ′ = 0 ГПа; 4 – D = 5 ГПа;
5 – D = 10 ГПа
Для идеального упругопластического материала данная полоса становится более узкой, аналогичный результат получен для материала с модулем разупрочнения 5 ГПа. Для модуля спада D = 10 ГПа в некоторый момент пластическая зона начинает резко вытягиваться, приобретая вид трещины, происходит потеря устойчивости численного решения.
Рассмотрим аналогичную задачу для пластины из упругопластического материала с участками линейного упрочнения ( E ′ = 50 ГПа) и разупрочнения ( D = 60 ГПа и 120 ГПа). Диаграммы деформирования материала представлены на рис. 4.
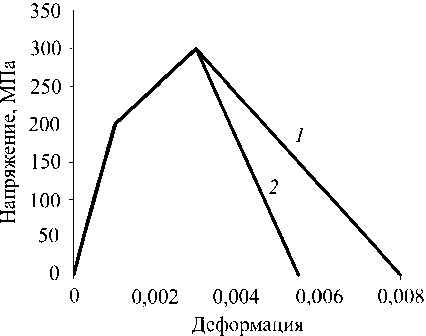
Рис. 4. Диаграммы деформирования: 1 – D = 60 ГПа; 2 – D = 120 ГПа
Fig. 2. Strain curves: 1 – E ′ = 100 GPa, 2 – E ′ = 25 GPa, 3 – E ′ = 0 GPa, 4 – D = 5 GPa, 5 – D = 10 GPa
Fig. 4. Strain curves: 1 – D = 60 GPa, 2 – D = 120 GPa
В результате моделирования получим набор полей перемещений, деформаций и напряжений для разных моментов времени. На рис. 3 показано, каким образом меняется пластическая зона для разных моделей материала. Для материала с упрочнением наблюдается широкая пластическая зона, расположенная под углом к направлению нагружения.
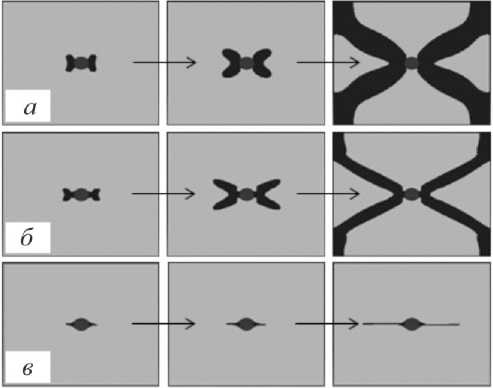
Рис. 3. Результаты расчета эволюции процесса деформирования пластины для диаграмм деформирования: а – с модулем упрочнения E ′ = 25 ГПа; б – с площадкой идеальной текучести E ′ = 0 ГПа; в – с модулем разупрочнения D = 10 ГПа
Fig. 3. Calculation results of plate deformation evolution for strain curves: a – with hardening module E ′ = 25 GPa, b – with perfect flow area E ′ = 0 GPa, c – with softening module D = 10 GPa
На рис. 5 показано, как меняются пластическая зона и зона закритического деформирования для нагружения с модулем разупрочнения D = 60 ГПа (темно-серый цвет – зона упрочнения, черный цвет – зона разупрочнения), для разупрочнения с модулем D = 120 ГПа зоны аналогичны. При уменьшении модуля спада зона закритиче-ского деформирования становится более выраженной. При прохождении магистральной трещины в ее вершине находится небольшая зона ослабленного материала.
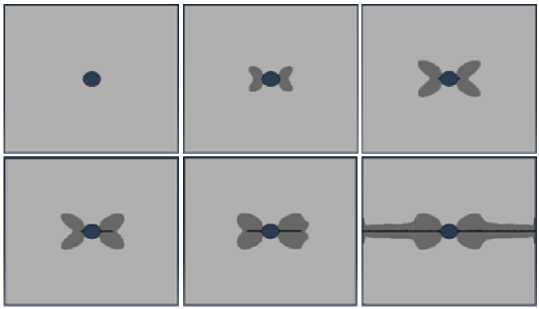
Рис. 5. Результаты расчета эволюции процесса деформирования и разрушения пластины
Fig. 5. Calculation results of plate deformation and destruction evolution
Рассмотрим эпюру напряжений σ22 вдоль горизонтальной оси симметрии, изображенную на рис. 6. На ней можно выделить несколько характерных точек: 1 – точка, где полностью реализована закритическая стадия деформирования материала; 2 – точка, соответствующая частичной реализации закритической стадии; 3 – точка, соответствующая пределу прочности материала; 4 – точка в области линейного упрочнения; 5 – точка, соответствующая границе пластической зоны (предел текучести); 6 – точка в упругой области. Из данного рисунка видно, каким образом реализуется диаграмма деформирования с учетом закритической стадии при данном нагружении.
R8
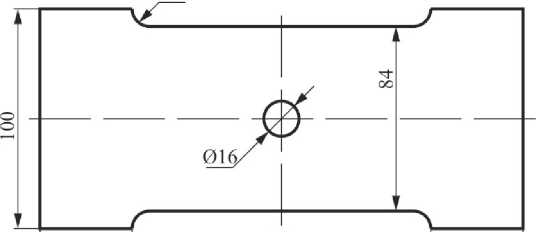
50 120
Рис. 7. Геометрия образца
Fig. 7. The sample’s geometry
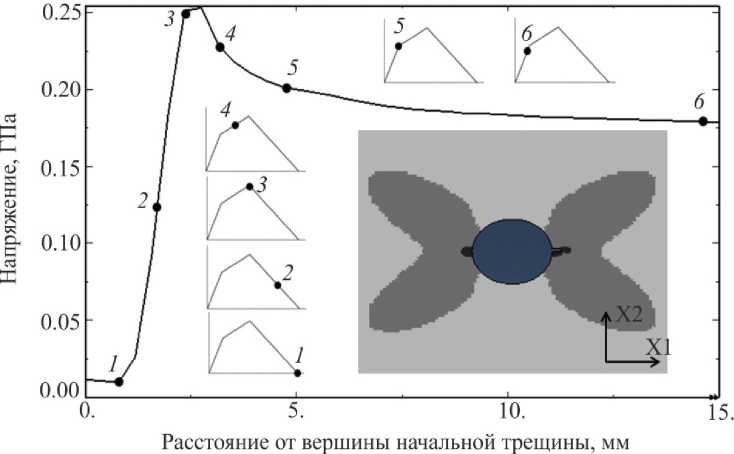
Рис. 6. Эпюра напряжений σ22 с соответствующими точками на диаграмме деформирования материала
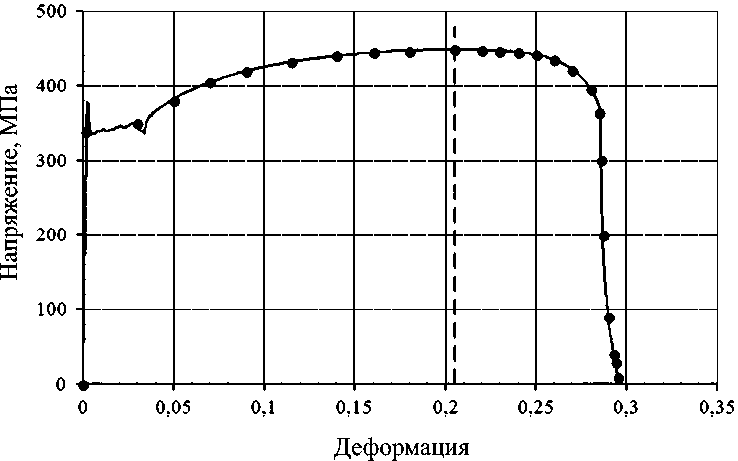
Рис. 8. Диаграмма деформирования стали 20
Fig. 6. Stress diagram σ22 with corresponding points on the material deformation diagram
Fig. 8. Steel 20 strain curve
Отмечено, что с уменьшением модуля разупрочнения происходит увеличение максимальной расчетной нагрузки, выдерживаемой конструкцией, система позже теряет устойчивость. Конструкция способна к увеличению прикладываемой внешней нагрузки даже при развитии зон закритического деформирования. Для диаграммы деформирования 1 увеличение нагрузки составило 2,1 % относительно расчета без учета закритической стадии деформирования. Следовательно, ее учет рационален для уточнения несущей способности конструкций.
-
4. Моделирование процесса деформирования пластины с концентратором напряжений при использовании реальных диаграмм деформирования
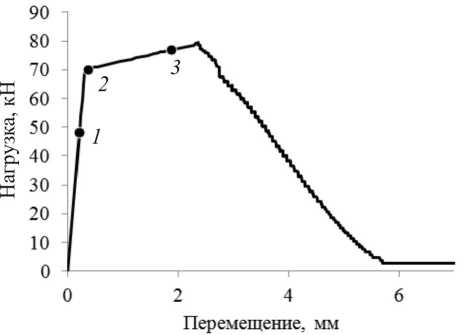
Рассмотрим процесс деформирования образца (геометрия изображена на рис. 7, толщина пластины 3 мм) из стали 20. Диаграмма деформирования материала приведена на рис. 8, на ней обозначены точки, по которым строится кусочно-линейная аппроксимация диаграммы деформирования, которая будет использована в численном анализе. Было принято, что по достижении последней точки из указанных на диаграмме он продолжает нести маленькую нагрузку.
К торцу (аналогично предыдущим задачам) прикладывалось перемещение 10 мм за условную единицу времени. Эволюция процесса деформирования пластины изображена на рис. 9.

Рис. 9. Результаты расчета эволюции процесса деформирования пластины из стали 20 (светло-серый цвет – зона с начальным упрочнением, темно-серый цвет – зона с развитым упрочнением, черный цвет – зона разупрочнения)
Fig. 9. Calculation results of a 20 steel plate deformation evolution (the light gray color shows the zone with initial hardening, the dark gray color shows the zone with developed hardening, the black color shows the zone of softening)
Построена расчетная диаграмма нагружения (рис. 10), она качественно соответствует экспериментальной [21]. Видно, что учет закритической стадии деформирования в данном случае позволяет получить выигрыш 2 % по нагрузке и 20 % по перемещению.
Рассмотрим процесс деформирования прямоугольной пластины 10×20 мм с центральным эллиптическим концентратором (большая и малая полуоси 2,5 и 1,25 мм соответственно) из стали 40Х. Диаграмма деформирования материала приведена на рис. 11, на ней обозначены точки, по которым строится кусочно-линейная аппроксимация диаграммы деформирования, которая будет использована в численном анализе.
лизация деформаций в узкую полосу. На рис. 14, 15 изображены поля напряжений σ 11 , σ 22 , σ 12 , σ i вблизи вершины концентратора напряжений для момента максимальной расчетной нагрузки (точка в на рис. 13) и момента потери численного решения (точка г на рис. 13): видно, что по мере приближения к вершине концентратора происходит уменьшение эквивалентных напряжений в связи с реализацией закритической стадии деформирования. Аналогичные результаты были получены в работе [27].
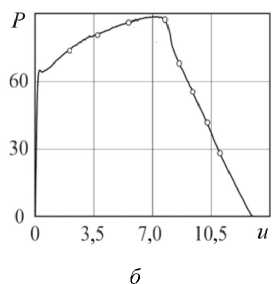
Рис. 10. а – Расчетная диаграмма нагружения: 1 – появление зоны с малым модулем упрочнения; 2 – появление зоны с большим модулем упрочнения; 3 – появление зоны закритического деформирования; б – экспериментальная диаграмма нагружения
Fig. 10. Calculated loading diagram: 1 ) the appearance of a zone with a small hardening modulus; 2 ) the appearance of a zone with a large hardening modulus; 3 ) the appearance of a zone of postcritical deformation; b the experimental loading diagram
На диаграмме деформирования можно выделить следующие участки: упругий, упрочнения, начального разупрочнения и развитого разупрочнения.
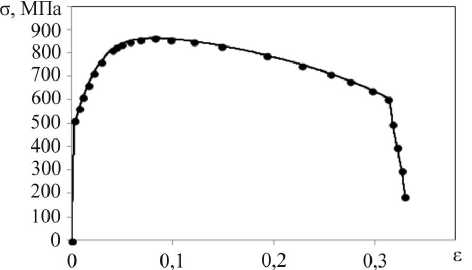
Рис. 11. Диаграмма деформирования стали 40Х; отмеченные точки заложены в модель
Fig. 11. Steel 40Cr4 deformation diagram; the marked points are embedded in the model
Результаты расчета эволюции процесса деформирования пластины изображены на рис. 12. Видно, как по мере деформирования появляется зона разупрочнения вблизи вершины концентратора. На расчетной диаграмме нагружения (рис. 13) видно, что рост нагрузки не останавливается после появления зоны разупрочнения; выигрыш по нагрузке составил 4,8 %, деформационный ресурс – 50,0 %. После достижения максимального значения нагрузки на образце наблюдается лока-

Рис. 12. Результаты расчета эволюции процесса деформирования пластины с эллиптическим концентратором из стали 40Х (светло-серый цвет – упругая область, серый цвет – зона упрочнения, темно-серый цвет – зона разупрочнения)
Fig. 12. Calculation results of the 40Cr4 steel plate with the elliptical concentrator deformation evolution (the light gray color shows the elastic area, the gray color shoes the hardening zone, the dark gray color shows the softening zone)
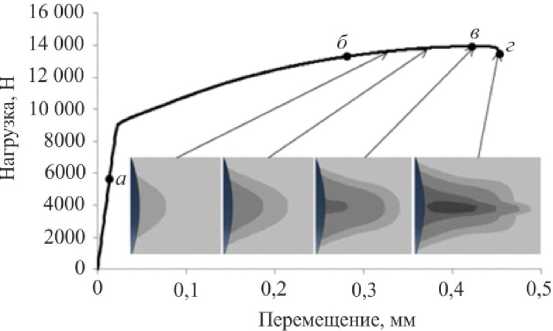
Рис. 13. Расчетная диаграмма нагружения: а – появление зоны упрочнения; б – появление зоны разупрочнения; в – точка с максимальной нагрузкой; г – точка срыва
Fig. 13. The calculated loading diagram: a ) the appearance of a hardening zone; b ) the appearance of a zone of softening; c ) the point with a maximum load, d ) the point of failure
Аналогичные задачи были решены для концентраторов напряжений иной геометрии: эллиптического, круглого, узкого прямоугольного, широкого прямоугольного, ромбовидного. Зоны закритического деформирования для максимального значения расчетной нагрузки приведены на рис. 16. Значения выигрышей по нагрузке и перемещению приведены в таблице. Видно, что учет закритической стадии деформирования позволяет выявить значительные прочностные и деформационные ресурсы конструкций с концентраторами напряжений.
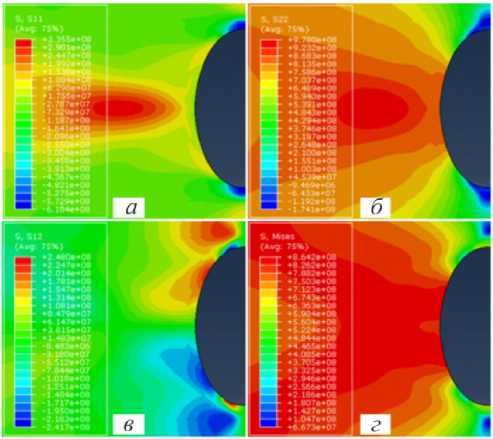
Рис. 14. Поля напряжений у вершины концентратора для точки с максимальной нагрузкой: a – σ11; б – σ22; в – σ12; г – σ i
Fig. 14. Fields of stresses near the top of the concentrator for the point with the maximum load: a – σ11; b – σ22; c – σ12; d – σ i
Выигрыши по нагрузке и перемещению для концентраторов разной геометрии
|
Номер концентратора |
Выигрыш по нагрузке, % |
Выигрыш по перемещению, % |
|
1 |
4,8 |
50,0 |
|
2 |
10,8 |
75,8 |
|
3 |
7,6 |
59,4 |
|
4 |
12,1 |
92,3 |
|
5 |
10,7 |
75,3 |
|
6 |
11,0 |
85,0 |
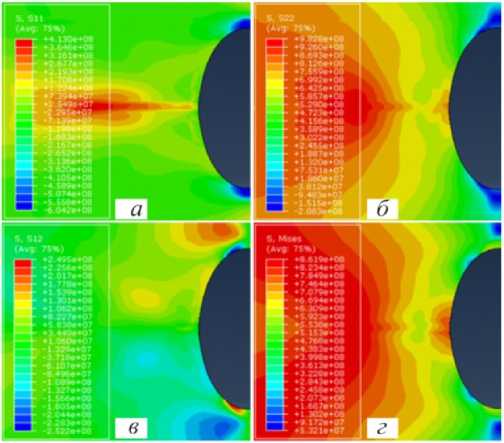
Рис. 15. Поля напряжений у вершины концентратора для точки срыва: a – σ11; б – σ22; в – σ12; г – σ i
Fig. 15. Fields of stresses near the top of the concentrator for the point of failure: a – σ11; b – σ22; c – σ12; d – σ i

Рис. 16. Зона разупрочнения для разных концентраторов: 1 , 2 – эллиптические; 3 – круглый; 4 – узкий прямоугольный;
5 – широкий прямоугольный; 6 – ромбовидный
Fig. 16. The softening zone for different concentrators:
1 , 2 ) elliptical; 3 ) round; 4 ) narrow rectangular; 5 ) wide rectangular; 6 ) diamond-shaped
Заключение
В работе получены новые численные решения задач о деформировании пластин с концентраторами напряжений различной геометрии. Рассмотрены двухзвенная и трехзвенная аппроксимации диаграммы деформирования, а также реальные диаграммы деформирования стали 20 и стали 40Х. Изучена эволюция процесса деформирования пластины с выявлением зон закритического деформирования материала. Построены расчетные диаграммы нагружения. Выявлены значительные прочностные и деформационные ресурсы при учете закритической стадии деформирования материала. Из всего вышеизложенного можно сделать вывод, что учет стадии разупрочнения материала целесообразен при проведении расчетов конструкций с концентраторами напряжений различной геометрии.
Экспериментальные исследования в рамках описания механического поведения различных сталей на за-критической стадии деформирования проводились в рамках Государственного задания Министерства науки и высшего образования Российской Федерации (№ ФСНМ-2020-0027). Экспериментальные исследования проведены с использованием УНУ «Комплекс испытательного и диагностического оборудования для исследования свойств конструкционных и функциональных материалов при сложных термомеханических воздействиях» ПНИПУ, модернизация которой осуществлялась при финансовой поддержке Минобрнауки России, Уникальный идентификатор проекта RFMEFI61920X0017.
Acknowledgements
The experimental studies in the framework of the description of the mechanical behavior of different steels at the stage of postcritical deformation were conducted within the State Assignment of the Ministry of Science and Higher Education of the Russian Federation (№ FSNM-2020-0027). Experimental studies were carried out using the large-scale research facilities “Complex of testing and diagnostic equipment for studying properties of structural and functional materials under complex thermomechanical loading” PNRPU modernized with funds by the Ministry of Science and Higher Education of the Russian Federation, Unique project identifier RFMEFI61920X0017.
Список литературы Моделирование процесса деформирования пластины с концентратором напряжений при учете закритической стадии деформирования материала
- Основы экспериментальной механики разрушения / И.М. Керштейн [и др.] – М.: Изд-во Моск. ун-та, 1989. – 140 с.
- Ломакин Е.В. Кручение цилиндрических тел с изменяющимися деформационными свойствами // МТТ. – 2008. – № 3. – С. 217–226.
- Bažant Z.P. Size effect on strength and lifetime probability distribution of quasibrittle structures // Sadhana. – 2012. – Vol. 37, iss. 1. – P. 17–31.
- Yu Q., Bazant Z.P. Shear strength of reinforced concrete beams: Size effect and its fracture-mechanics basis // American Concrete Institute, ACI Special Publication. – Vol. 2015. – January. – Iss. SP 300. – P. 143–174.
- Никитин Л.В. Закритическое поведение разупрочняющегося материала // Докл. АН. – 1995. – Т. 342, № 4. – С. 487–490.
- Effect of complex combined loading mode on the fracture toughness of titanium alloys / M.G. Chausov, P.O. Maruschak, V. Hutsaylyuk, L. Śnieżek, A.P. Pylypenko // Vacuum. – 2018. – Vol. 147. – P. 51–57.
- Tsvetkov A.B., Pavlova L.D., Fryanov V.N. Construction of the approximant of complete diagram for rock deformation // IOP Conference Series: Earth and Environmental Science. – 2016. – Vol. 45, iss. 1.
- Struzhanov V.V., Korkin A.V. The stability of the deformation of one of the farm with the softening of the material elements // CEUR Workshop Proceedings. – 2016. – Vol. 1825. – P. 180–187.
- Савицкий Ф.С., Вандышев Б.А. Жесткость испытательных машин и ее влияние на спадающий участок диаграммы растяжения и изгиба // Заводская лаборатория. – 1956. – Т. 22. – С. 717–721.
- Линьков А.М. Об условиях устойчивости в механике разрушения // Докл. АН СССР. – 1977. – Т. 233, № 1. – С. 45–48.
- Вильдеман В.Э., Соколкин Ю.В., Ташкинов А.А. Механика неупругого деформирования и разрушения композиционных материалов / под ред. Ю.В. Соколкина. – М.: Наука: Физматлит, 1997. – 288 с.
- Вильдеман В.Э. О решениях упругопластических задач с граничными условиями контактного типа для тел с зонами разупрочнения // ПММ. – 1998. – Т. 62, № 2. – С. 304–312.
- Волков С.Д., Дубровина Г.И., Соковнин Ю.П. Устойчивость сопротивления материала в механике разрушения // Проблемы прочности. – 1978. – № 6. – С. 65–69.
- Экспериментальные функции сопротивления легированной стали при растяжении и кручении / С.Д. Волков [и др.] // Проблемы прочности. – 1979. – № 1. – С. 3–6.
- Лебедев А.А., Чаусов Н.Г. Установка для построения полностью равновесных диаграмм деформирования // Проблемы прочности. – 1981. – № 12. – С. 104–106.
- Лебедев А.А., Чаусов Н.Г., Евецкий Ю.Л. Методика построения полных диаграмм деформирования листовых материалов // Проблемы прочности. – 1986. – № 9. – С. 29–32.
- Setup for testing materials with plotting complete stressstrain diagrams / N.G. Chausov, D.G. Vojtyuk, A.P. Pilipenko, A.M. Kuz'menko // Problemy Prochnosti. – 2004. – Iss. 5. – P. 117–123.
- Chausov N.G. Full deformation diagram as source of information about accumulation of damages and material crack resistance // Zavodskaya Laboratoriya. Diagnostika materialov. – 2004. – Vol. 70, iss. 7. – P. 42–49.
- Вильдеман В.Э., Третьяков М.П. Экспериментальное изучение закритического деформирования и разрушения сталей при высоких температурах // Вестник Пермского национального исследовательского политехнического университета. Механика. – 2019. – № 1.
- Бородулина Т.П. Применение цифровой оптической системы VIC-3D для определения жесткости нагружающей системы универсальной испытательной машины ZwickZ100 // Молодежный научно-технический вестник. – 2016. – № 10. – С. 20.
- Экспериментальные исследования закритического деформирования и разрушения конструкционных материалов / В.Э. Вильдеман, Е.В. Ломакин, М.П. Третьяков, Т.В. Третьякова, Д.С. Лобанов. – Пермь: Изд-во ПНИПУ, 2018. – 156 с.
- Ибрагимов В.А., Клюшников В.Д. Некоторые задачи для сред с падающей диаграммой // Механика твердого тела. – 1971. – № 4 – С. 116–121.
- Никитин Л.В., Рыжак Е.И. Закономерности разрушения горной породы с внутренним трением и дилатансией // Изв. АН СССР. Физика Земли. – 1977. – № 5. – С. 22.
- Волков С.Д., Дубровина Г.И., Соковнин Ю.П. О краевой задаче механики разрушения // Проблемы прочности. – 1978. – № 1. – С. 3–7.
- Стружанов В.В. О разрушении диска с центральной ослабленной зоной // Изв. АН СССР. МТТ. – 1986. – № 1. – С. 135–141.
- Вильдеман В.Э., Мугатаров А.И. Задача о кручении цилиндрического тела с учетом разупрочнения // Вестник Пермского национального исследовательского политехнического университета. Механика. – 2019. – № 4. – С. 29–36.
- Радченко В.П., Горбунов С.В. Метод решения краевой упругопластической задачи о растяжении полосы с концентраторами напряжений с учетом локальных областей пластического разупрочнения материала // Вестн. Самар. гос. техн. ун-та. Сер. Физ.-мат. науки. – 2014. – № 4. – С. 98–110.
- Радченко В.П., Горбунов С.В. Численное решение плоской краевой задачи закритического упругопластического деформирования полосы с концентраторами напряжений // Математическое моделирование и краевые задачи. – 2016. – С. 178–182.
- Феклистова Е.В., Вильдеман В.Э. Моделирование процессов закритического деформирования и разрушения тел с концентраторами различной геометрии // Механика, ресурс и диагностика материалов и конструкций. – 2018. – С. 413
- Феклистова Е.В. Численное исследование процессов деформирования и разрушения тел с концентраторами напряжений на стадии закритического деформирования // Аэрокосмическая техника, высокие технологии и инновации. – 2017. – Т. 1. – С. 283–285.
- Ильюшин А.А. Пластичность. Ч. 1. Упругопластические деформации. – М: Изд-во ОГИЗ, 1948. – 376 с.


