Моделирование процесса деформирования подводного газопровода под действием взрывной нагрузки

ВЕСТНИК ПНИПУ. МЕХАНИКА № 2, 2024PNRPU MECHANICS BULLETIN

В настоящее время широкое распространение получили подводные трубопроводы высокого давления, в частности газопроводы «Северный поток» и «Северный поток – 2», представляющие собой стальную трубу (СТ), покрытую защитным слоем высокопрочного бетона, удерживающим газопровод на дне и фиксирующим трубу. Эти трубопроводы в сентябре 2022 г. подверглись террористической атаке и частично были разрушены взрывами. Проблемы воздействия взрывных нагрузок на подводные элементы конструкций рассматривались в работах [1–4]. В данной статье рассматривается задача ударного воздействия на фрагмент газопровода взрыва сферического заряда взрывчатого вещества (ВВ) октогена, инициированного в центре заряда. Для моделирования задач используются уравнения динамики сплошных сред и авторский пакет программ [5– 7], реализованный на языке фортран с технологией распараллеливания openMP. Система решаемых уравнений включает законы сохранения массы, импульса, энергии и физические соотношения упругости и пластичности с учетом больших перемещений и поворота тензора напряжений в эйлеровых переменных – производная Яуманна [8], записанные в дифференциальной форме [9]. При отсутствии сдвиговых напряжений система переходит в уравнения Эйлера для сжимаемой жидкости или газа [10]. К уравнениям добавляются начальные и краевые условия. На границах контактных поверхностей тел ставятся условия непроникания и отсутствия трения. В этом случае на контактной поверхности отсутствуют сдвиговые напряжения и полагаются равными нормальные компоненты скоростей взаимодействующих сред. Для описания процессов в плотных сжимаемых средах (сталь, бетон) применяется баротропное уравнение состояния (УРС) вида p= p(ρ), связывающее давление p и плотность среды ρ, позволяющее избежать интегрирования уравнения сохранения энергии. Для среды с плотностью ρ0 это будет УРС идеального упругопластического тела p =Κεv для шаровых компонент, где K – модуль объемного сжатия, εv=1-ρ0/ρ – объемная деформация. Критерием перехода из упругого напряженно-деформированного состояния в пластическое является условие текучести Мизеса: J2 = 0,5 Sij Sij ≥ (1/ 3)σТ2 , где J2 – второй инвариант девиатора тензора напряжений, σТ – предел текучести. В случае этого условия происходит коррекция компонент девиатора в соответствии с [11–14]. Для воды используется уравне-p+B    c2

ние состояния в форме Тейта [15; 16] ε= ⁰ - ⁰, ( γ- 1) ργ- 1

где ε – внутренняя энергия единицы массы, γ – показатель адиабаты, B0, c0 – некоторые константы. Для численного решения уравнений применяется модификация схемы Годунова повышенной точности [17; 18], первоначально предложенной для решения нелинейных динамических задач гидрогазодинамики [10]. В отличие от существующих в настоящее время многочисленных модификаций схемы Годунова повышенной точности для упругопластических течений, в частности, работы [20– 25], модификация [17; 18] практически едина как для газодинамических, так и упругопластических течений, причем повышение точности достигается на компактном пространственном шаблоне. Модификация использует точное решение задачи распада разрыва на контакте «жидкость – упругое тело» и метод расщепления [12–14] для расчета пластической составляющей течения. Для моделирования процесса распространения детонации в заряде октогена применяется гидродинамическая теория детонации [25] и лучевая модель распространения [26–31]. Для продуктов взрыва (ПВ) зависимость показателя адиабаты γ от ρ принимается в виде:

γ(ρ)= ρ0/ρR1Aexp(-R1ρ0/ρ)+ρ0/ρR2Bexp(-R2ρ0/ρ)+C(1+ω)(ρ/ρ0)1+ω Aexp(-R1ρ0/ρ) +Bexp(-R2ρ0/ρ) +C(ρ/ρ0)1+ω           , полученной в предположении равенства скоростей звука для ПВ с использованием УРС идеального газа и УРС типа JWL [32; 33]. R1, R2, ω, A, B, C – константы ВВ для УРС типа JWL, D – скорость установившейся детонации, pн – давление на фронте детонационной волны. Для октогена эти константы приведены в таблице.

Константы октогена для УРС типа JWL

HMX constants for JWL type EOS

ВВ	ρ 0 , кг/м3	D , м/с	р Н , ГПа	R 1	R 2	ω	A , ГПа	В , ГПа	С , ГПа
Октоген	1891	9110	42,0	4,2	1,0	0,30	778,3	7,071	0,643

1. Численное моделирование процесса взрывного нагружения подводного трубопровода

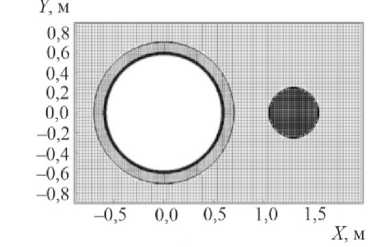
Постановка задачи приведена на рис. 1. Рассматривался участок трубопровода длиной 6 м, внутренний диаметр и толщина стальной трубы соответственно 1,15 и 0,027 м (внешний радиус R = 0,5885 м), толщина бетонного покрытия (БП) 0,1 м. Предполагается, что нижняя часть трубопровода находится над жестким дном на высоте 0,198 м (ось трубопровода проходит на высоте 0,9 м от дна). Центр сферического заряда диаметром 0,5 м и массой 123 кг находится на высоте 0,65 м от дна на расстоянии 1,3 м от оси трубопровода (от поверхности заряда до бетонного покрытия трубы – 0,35 м). Инициация ВВ происходит в центре заряда. Размеры расчетной области 0,29×2×6 м, на искусственных внешних границах области (СТ, БП, вода) ставятся условия «свободного вытока» [10]. Реализация этих условий осуществляется присвоением граничным значениям параметров из прилегающих ячеек.

Данные граничные условия позволяют исключить влияние искусственных границ трубопровода на процессы, происходящие в области его максимального деформирования до 1,5 мс. Начало координат находится на оси Z в середине трубы. В начальный момент давление во всех средах и внутри трубопровода полагалось равным 0,1 МПа. На рис. 1, а , изображена поверхностная сетка (STL-файлы всех объектов, кроме воды) по стальной трубе, бетонному покрытию и сферическому заряду ВВ; также изображена жесткая поверхность дна; всего, включая воду, порядка 600 тысяч треугольников. На рис. 1, b , приведена основная кубическая расчетная сетка (сечение в плоскости Z =0) по СТ, БП, воде и ВВ, размеры ячеек сетки по каждой среде соответственно 0,005, 0,02, 0,03 и 0,02 м, всего – порядка 14 млн ячеек. Выбор данной сетки и граничных условий был произведен после ряда предварительных расчетов с оценкой влияния действия прямых и отраженных ударных волн на трубопровод с тем, чтобы исключить возможное нефизичное влияние близко расположенных границ расчетной области.

b

Рис. 1. Поверхностная сетка ( a ); сетка в сечении Z =0 ( b )

Fig. 1. Surface mesh ( a ); mesh in section Z =0 ( b )

Механические характеристики двухслойного трубопровода: сталь Х70 и бетон с железорудным наполнителем [34; 35], плотности 7850 и 2500 кг/м3, объемные модули упругости 168 и 22,2 ГПа, модули сдвига 77,7 и 15 ГПа, пределы текучести 500 и 80 МПа соответственно. Предполагается идеальная пластичность этих сред. Ввиду кратковременности нагрузок для бетона предполагалось равенство модулей на сжатие и растяжение. Для воды в уравнении Тета показатель адиабаты γ=7,15, В0 = 304,5 МПа, с0 = 1450 м/c, и эти параметры полагались постоянными в процессе всего нагружения. Октоген был выбран как одно из наиболее мощных используемых взрывчатых веществ. Расчеты проводились на компьютере с процессором i9-13900K (24 ядра, 32 потока) до времени 1,6 мс, соответствующему окончанию основной взрывной нагрузки. Расчет одного варианта занимал порядка 50 ч. Ударная волна от расширяющихся продуктов взрыва распространяется по водной среде и нагружает БП, которое, в свою очередь, взаимодействует с СТ. Наблюдается достаточно сложная нелинейная картина взаимодействия волн.

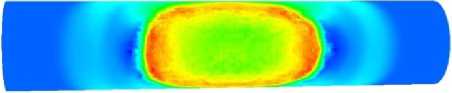
0            0,5 ГПа

a

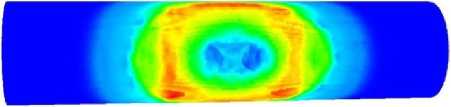
0           0,35 ГПа

b

Рис. 2. Давление на поверхности трубопровода в момент времени 0,5 мс: а – СТ; b – БП

Fig. 2. Pressure on the surface of the pipeline at a time of 0.5 ms: a – ST; b – BP

Скорости распространения возмущений по СТ и БП выше, чем в воде, но амплитуда их существенно меньше, чем от головной ударной волны. Для более близкого расположения заряда ВВ к трубопроводу на момент 0,5 мс распределение давления на поверхности СТ и БП показано на рис. 2, а , и b соответственно. Область максимального давления на СТ практически совпадает с областью максимального нагружения БП головной ударной волной. Возмущения, распространяющиеся по СТ с большей скоростью, на момент 0,5 мс еще не достигают концов СТ.

На рис. 3, а, b, показаны давления от времени на поверхности БП и на СТ соответственно (здесь и далее под поверхностью БП и СТ понимается внешняя поверхность БП и СТ) в ближайших к заряду точках трубопровода для двух положений зарядов на расстоянии 0,6 и 0,7 м от центра заряда до БП. Сплошными линиями показано давление для расстояния от центра заряда 0,6 м, штриховыми – для 0,7 м. Максимальное давление на СТ оказывается несколько выше, чем на БП, что связано с большей жесткостью стали, чем бетона. При разгрузке также наблюдается различие, связанное с тем, что сталь разгружается в бетон, а бетон в менее плотную среду – воду. Следует отметить, что влияние падения давления на поверхность СТ существенно меньше, чем на поверхность БП. На рис. 4 приведены радиальные скорости на поверхности СТ (положительные в сторону центра трубы), сплошной линией для ближнего расположения заряда, пунктирной – для дальнего.

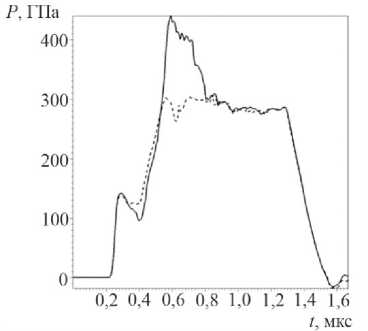
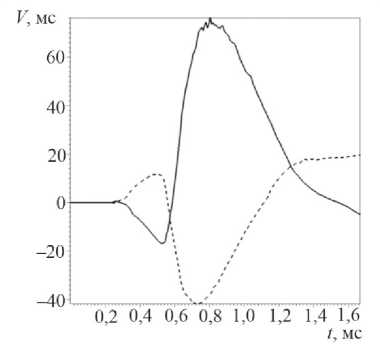
На рис. 5 показаны зависимости давления и вертикальные скорости от времени на поверхности СТ в сечении Z =0 в точке, ближайшей ко дну и диаметрально противоположной. Отличия в поведении кривых вызваны влиянием отраженной от дна волны.

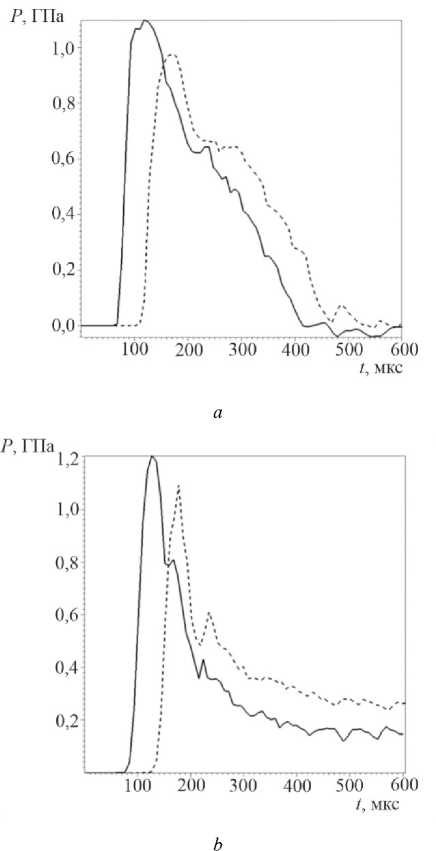
Рис. 3. Давление на поверхности в сечении Z =0, сплошная линия – от ближнего расположения заряда, штриховая – от дальнего: a – на БП; b – на СТ

Fig. 3. Pressure on the surface in section Z =0, the solid line is from the near charge location, the dashed line is from the far one: a – at BP; b – at ST

Нижняя точка, более близкая ко дну, приобретает значительно большую вертикальную скорость, чем верхняя точка. Аналогичный эффект наблюдается и для горизонтальных скоростей, но в меньшей степени.

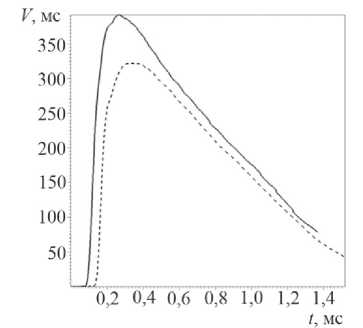
Рис. 4. Скорости на поверхности СТ в сечении Z =0 в ближайшей к заряду точке, сплошная от ближнего расположения заряда, штриховая – от дальнего

Fig. 4. Speed on the surface of the ST in the section Z =0 at the point closest to the charge, solid from the nearest location of the charge, dashed from the further one

b

Рис. 5. Давления и скорости на поверхности СТ: а – давления; b – вертикальные скорости СТ в точках, имеющих в начальный момент координаты X =0, Z =0, Y = ± R ; (низ и верх трубы), сплошная при Y = - R , штриховая при Y = + R

Fig. 5. Pressures and velocities on the surface of the ST: a – pressure; b – vertical velocities of the ST at points that at the initial moment have coordinates X =0, Z =0, Y = ± R ; (bottom and top of pipe), a solid line is for Y= - R , a dashed line is for Y= + R

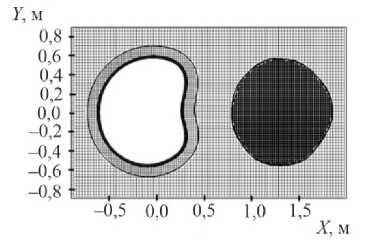
На рис. 6, а , показаны расчетные сетки в сечении Z =0 на момент времени 1,6 мс. На рис. 6, b , в сечении Z =0 приведены штриховыми линиями начальные формы заряда и СТ, сплошными линиями – эти формы на момент времени 1,6 мс.

Можно отметить большие перемещения деформирующегося трубопровода и газовой полости, занятой продуктами детонации. В сечении Z =0 наблюдаются максимальные изгибы трубопровода, где окружные деформации растяжения к моменту времени 0,5 мс превышают 20 % и продолжают расти до расчетного времени 1,6 мс, аналогичным образом в этих точках ведут себя деформации по толщине трубы. Следовательно, в этих областях происходит разрушение стальной трубы. На внешнем слое БП также возникают большие положительные деформации, превышающие 5 %, что также ведет к разрушению БП. Таким образом, накопляющийся уровень деформаций при заданной нагрузке приводит к разрушению трубопровода.

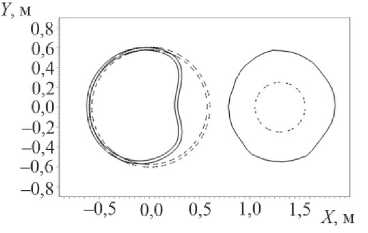
b

Рис. 6. Расчетные сетки на момент 1,6 мс в сечении: а – Z =0; b – начальное положение заряда ВВ и стальной трубы показано штриховыми, сплошными на момент времени 1,6 мс

Fig. 6. Calculation grids at the moment of 1.6 ms in the section: a – Z =0, b – the initial position of the explosive charge and the steel pipe is shown as dashed and solid lines at the time of 1.6 ms

Заключение

На основе разработанной авторской численной методики и соответствующего программного обеспечения решения трехмерных задач динамики сплошных сред проведено моделирование взаимодействия двухслойного трубопровода с ударными волнами в окружающей жидкости от близкого взрыва сферического заряда октогена весом 123 кг для двух положений заряда. Расчет ведется в эйлеровых переменных с выделением лагранжевых контактных поверхностей. В связанной постановке описывается процесс взрывного нагружения трубопровода вблизи жесткого дна, включая распространение детонации в твердом ВВ с последующим расширением газового пузыря с продуктами детонации, его расширением в окружающую жидкость с формированием ударных волн,