Моделирование процесса дозированной выдачи измельченных стебельных кормов
Автор: Глобин Андрей Николаевич
Журнал: Вестник аграрной науки Дона @don-agrarian-science
Рубрика: Технологии, средства механизации и энергетическое оборудование
Статья в выпуске: 1 (37), 2017 года.
Бесплатный доступ
Процесс выдачи измельченных стебельных кормов можно представить как отделение частиц от бурта движущимся кормоотделителем и формирование корма на плоскости. Основным функциональным показателем работы дозирующего устройства является равномерность выдачи Θ, которая оценивается отклонением массы порции от среднего значения. Равномерность выдачи корма зависит от его физико-механических свойств, расположения в бункере, конструктивно-технологической схемы оборудования. Она понижается с увеличением длины частиц корма, их массы, площади кормоотделения, колебаний плотности, влажности и геометрии поперечного среза кормового потока, а также из-за снижения плотности корма и производительности. Математическое моделирование дозированной выдачи измельченных стебельных кормов показывает, что фракционный состав корма существенно влияет на формирование порции. Различное расположение частиц в пространстве (как в горизонтальном, так и в вертикальном направлениях) при ограничении свободы по горизонтали приводит к отклонению высоты порции. Моделирование процесса формирования порции измельченного стебельного корма свидетельствует о влиянии фракционного состава корма на равномерность выдачи. Адекватность разработанной модели влияния фракционного состава измельченного стебельного корма и его физико-механических свойств на равномерность выдачи подтверждают полученные экспериментальные данные, где влияние фракционного состава корма определялось экспериментальными исследованиями.
Дозирование, дозатор, дозирующее устройство, равномерность выдачи корма, колебание плотности порций, математическое ожидание, дисперсия, среднее квадратичное отклонение, площадь кормоотделения
Короткий адрес: https://sciup.org/140204409
IDR: 140204409 | УДК: 631.363
Текст научной статьи Моделирование процесса дозированной выдачи измельченных стебельных кормов
Введение. Неотъемлемой частью экономического благосостояния государства и приоритетным направлением национальной политики является обеспечение населения качественными продуктами питания в широком ассортименте и достаточном количестве. Решение этих вопросов во многом зависит от состояния и условий функционирования отрасли животноводства, которая претерпела существенные изменения в ходе проводимых реформ. Принятые в последние годы меры по поддержке агропромышленного комплекса и, в частности, отрасли животноводства, такие как финансовое оздоровление предприятий, субсидирование процентной кредитной ставки, развитие лизинга, реализация приоритетного национального проекта «Развитие АПК», Федерального закона «О развитии сельского хозяйства» и другие, позволили несколько улучшить ситуацию. Падение объемов производства было приостановлено, наметился определенный рост, но коренного перелома в состоянии отрасли животноводства пока не произошло [1].
Главным инструментом, призванным обеспечить достижение программных целей, является, прежде всего, обеспечение конкурентоспособности отрасли в условиях членства России во Всемирной торговой организации посредством повышения продуктивности скота и птицы, расширения внедрения индустриального способа производства, породного обновления животных и птицы, развития социально значимых отраслей: овцеводства, козоводства, коневодства, птицеводства, звероводства [1].
В мировой практике считается, что молочная продуктивность животных на 60% зависит от кормов. Выращивание дешёвых кормов обеспечивает относительно низкую себестоимость животноводческой продукции. Определяющую роль при этом играют набор кормовых культур и качество кормов. В зависимости от питательной ценности и с учетом аспектов использования они подразделяются на основные и концентрированные.
Основными считаются корма собственного производства. К этой группе от носятся зелёные корма и продукты их консервирования - сенаж, зерносенаж, силос, сено, солома и прочие. При организации кормопроизводства и кормозаготовки необходимо учитывать, что не менее 50% потребности молочной коровы в питательных веществах должны покрываться за счёт основного корма [1,2].
Описание математической модели и ее обсуждение. Согласно методическим принципам обеспечения качества продукции животноводства на этапе проектирования продукции путем обоснования технологических решений, как подсистемы обеспечения качества, разработана модель оптимизации технологических процессов приготовления кормов на животноводческих фермах [3, 4].
Она является стрежнем общей модели производства продукции и основана на моделировании функциональных показателей качества технологических процессов приготовления и конверсии кормов в продукцию животноводства в зависимости от качества их подготовки к скармливанию [3, 4].
Процесс выдачи измельченных стебельных кормов можно представить как отделение частиц от бурта движущимся кормоотделителем и формирование корма на плоскости.
Основным функциональным показателем работы дозирующего устройства является равномерность выдачи Ө, которая оценивается отклонением массы порции от среднего значения Тр [5, 6, 7, 8]:
Ө = -^х100%, (1)
где t - уровень значимости, обусловленный степенью свободы k = п - 1 и уровнем вероятности Р = 0,95;
crz - среднее квадратичное отклонение массы порций;
тп - математическое ожидание массы порции.
Отклонение массы порций зависит от ее геометрических параметров (<т ), колебаний плотности (отр ) и влажности корма (сгтйТ), а также конструктивно-технологи- ческих параметров дозирующего устройства (^)-
Колебание плотности порции, а следовательно, и ее массы также зависит от фракционного состава и расположения частиц в объеме порции (ст* ) (рисунок 1).
Геометрические параметры сформированной порции зависят от колебания формы и размера поперечного сечения порции корма, который подается на кормо-отделитель, ширины В, высоты Н и длины Ln порции и результата взаимодействия ее частиц с частицами соседней порции [5, 7].
Вследствие независимости вышеперечисленных факторов друг от друга среднее квадратичное отклонение Ок порций выражается [11, 12] зависимостью
°S - V^ + ^ + ^mw + °",«Я + ^ • (2)
Количество частиц в объеме порции из-за различного их расположения не является постоянным. Для количественной оценки равномерности массы порции, которая возникает под влиянием этого фактора, принимаем следующие допущения: частица принадлежит пласту, если ее середина расположена в пласте, а высота пласта равняется среднему диаметру частицы.
Определив размер площади пласта, в котором располагается известное количество частиц, выявляем условную площадь Fej, которая приходится на одну частицу, а точнее, условную площадь, в зоне которой располагаются центры частиц:
Ң п^гц Fe' = BL^ph^
где Vx - единичный объем порции с известным количеством частиц т;
Ис1 - высота единичного пласта порции;
-
т. - масса /-ой частицы корма;
-
п, - количество частиц /-го размера в объеме порции Гц
-
В, Ln - ширина и длина порции;
-
р - плотность корма;
-
а, - сторона квадрата условной площади, которая приходится на одну часть длины частицы.
Положение близлежащих частиц (рисунок 2) определяется расстоянием между их центрами в системе координат х и у и углом ф' их пересечения, а поэтому пересечение возможно при определенных условиях.
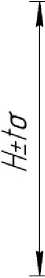
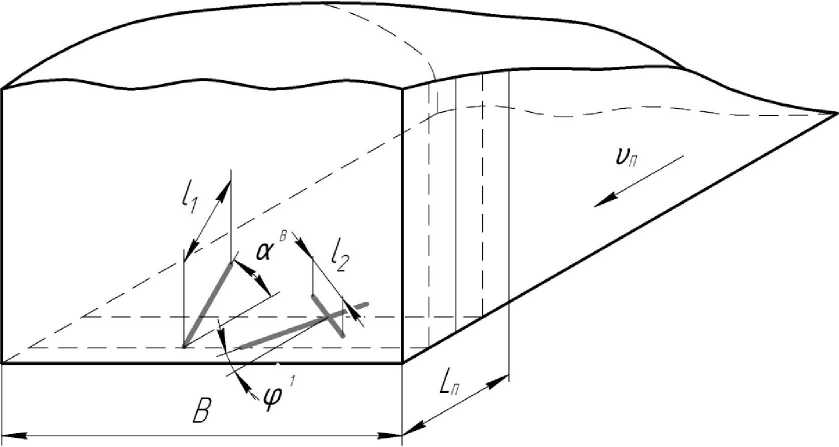
Рисунок 1 - Схема расположения частиц корма в порции
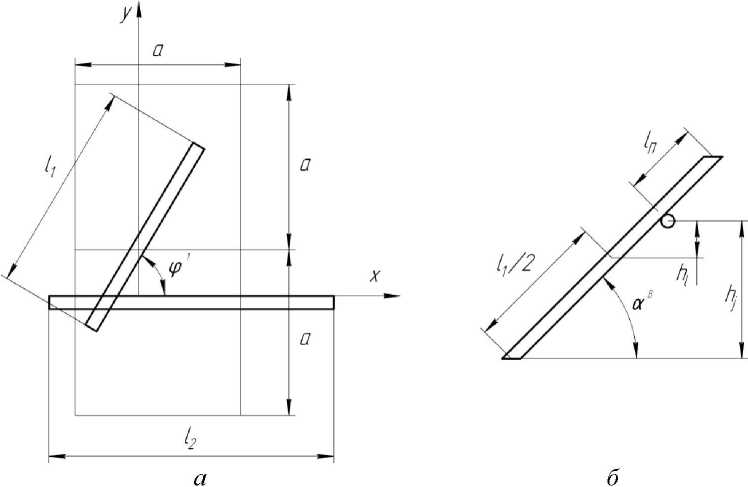
Рисунок 2 - Схема расположения частиц в горизонтальной (а) и вертикальной (б) плоскостях
Пересечение частиц, когда 0,5^ <2а и la>f7, происходит при расположении центров частиц в пределах 0 > х < а, (х-0,582)ctg^9' >у < (х +0,5 в ус^ф' и угла пересечения частиц ф’ , изменяющегося от
0 до 71. Поэтому математическое ожидание Г и дисперсия D, [13, 14, 15] пересечения частиц определяется выражениями:
«ал ^ММДгФ 7 п Л
/” =---- ^dx I" d^ I" — ——— \dy;
^^ 0 0 2 sin ф J
«ал ^O.Sts'ygcp Z \2
D, = —-^х^ф’ [ \—-^^\dy-UnJ.
* W^ J A 2 sin^'J v 7
0 0
(x-0,5^2
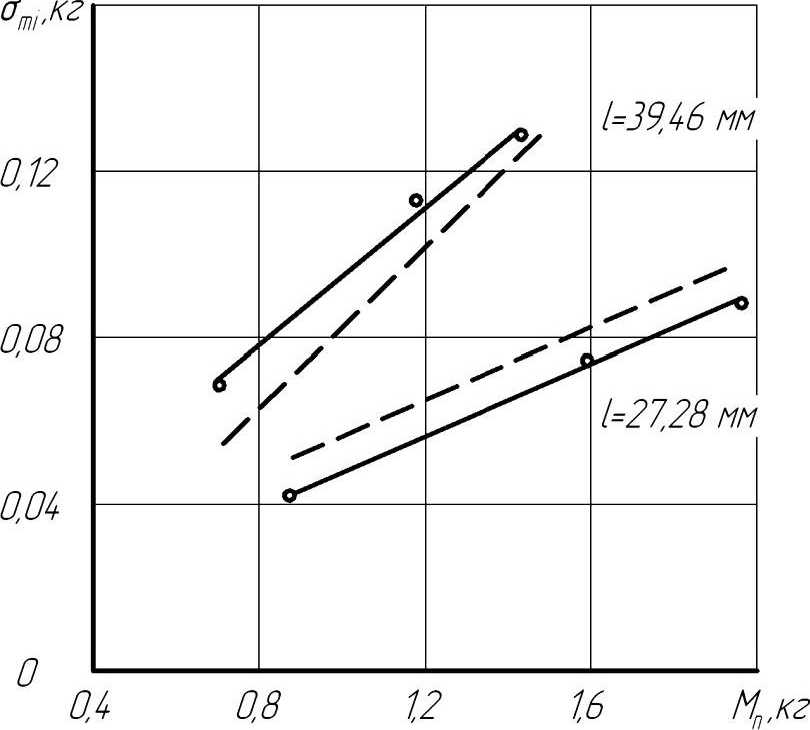
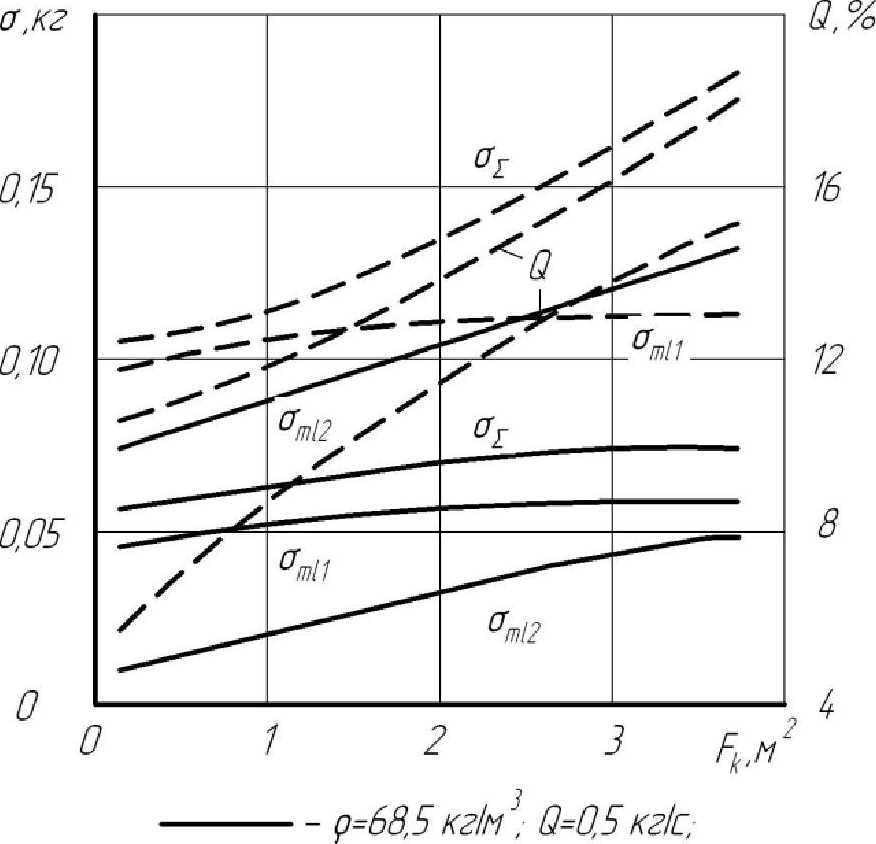
)tg Для случая txa пересе чение происходит при расположении центров частиц в пределах 0 > х < а, 0> у <0,5С18хпф', а угла ф' - в пределах от 0 до 0,5 71. Тогда А а 2 "-5/ -мпу// ^гМ*' 1" ^ U7t4 0 0 о k z У sin^' v .аб 0,5Қ8Іп<р'z ----f dx f dqd f — a7I^-\ oo 0 k 2 Для случая, когда 0,5^ >Та и t2 пересечение происходит при 0<х<а, гх л-0,5^7 , т + 0,5^, 0 < у < Та и arctg-------- < ф < arctg-------- . ' ' У У При этом: sin ф ; В этом случае возможно использование и другого метода определения значений €” и De. Расстояние между центрами частиц зависит от расположения их на условной площади Ғй -а2. В каждом случае положения центров определяются координатами х у", а положение второй частицы €2 определяется углом ати наклона линии, которая соединяет центры частиц. Математическое ожидание пересеченной части €" частицы €2 определяется как 0,51, -а . Дисперсия пересеченной части частицы I, определяется как сумма дисперсий D^ и D^ , которые зависят от расположения центров частиц €, и € 2 и от угла а^ расположения частицы £ 2 соответственно. Дисперсия расстояния между центрами определяется суммой дисперсий расстояний расположения центров от границы площадей. При равенстве слагаемых эта величина удваивается по отношению к дисперсии расстояния расположения центра от границы условной площади: (Ю) где атй - угол наклона линии, соединяющей центры частиц. Дисперсию De, которая зависит от угла at расположения частицы €2 и расположения точки пересечения частиц на €2, можно представить как случайное расположение точки в окружности диаметром г = €2 В других случаях пересечение их происходит, когда расположение центров частиц определяется параметрами: 0 > х < а, 0 > у < 0,5€, sin(9, а угол меняется в пределах т + 0,512 , х- 0,512 arccos-------- >ф< arccos--------. 0,5€, 0,5€ , Тогда математическое ожидание и дисперсия пересеченной части частиц определяются выражениями: - a 0,5€j 0,5€1sin^'/ \ €” =---\dф, Г —----—\dy; 2™ I '+0,5^ Jo sin <9'J arccos-------- Для всех случаев, кроме тех, где 0,5£ [ > 2а, дисперсию можно определять как D(i = (o,lllxZ^. Для определения отклонения расположения центров части по вертикали рассмотрим случай, когда падающая частица одним концом опирается на частицу, лежащую на корме, а вторым равномерно за нимает положение в пространстве (рисунок 2). Угол наклона частицы зависит от высоты hj расположения частицы, ее длины £, и величины Г пересеченной части. Тогда математическое ожидание Һ и дисперсия Вы высоты расположения центра частицы определятся выражениями: для (^-C^hj Для sin б/ dec - /г,2,. Дисперсия Dr высоты порции, кото- странстве, определяется отклонениями уг- рая зависит от расположения частиц в про- ла !/ и размером сечения части: где п - количество пластов в порции; Ncl - количество частиц в пласте; Ре - вероятность расположения частиц граничных порций с пересечением. Тогда среднее квадратичное отклонение объема порции, вызванное изменением ее высоты, определяется формулой V Nd ■ Ki где Н, В, Ln - соответственно высота, ширина и длина порции корма. Известно, что среднее квадратичное отклонение массы порции crmZ , которая зависит от расположения частиц в объеме порции, определяется выражением <7тк = . (22) Учитывая среднее квадратичное отклонение массы порции (22), а соответственно расположение частиц в объеме и взаимное пересечение порций (рисунок 1), которое зависит от количества частиц, пересекающих плоскость деления этих порций, получаем выражение среднего квадратичного отклонения массы порции, зависящего от фракционного состава корма. Подставляя в него полученные ранее выражения средних квадратичных откло- нений составляющих неравномерности в (1) и (2), получаем выражение функцио- нального показателя качества подачи измельченного стебельного корма - равно- мерности подачи: ^тах П У -- \ £1 I И ) -IT 1 Полученные выражения показывают, что равномерность выдачи корма зависит от его физико-механических свойств, расположения в бункере, конструктивнотехнологической схемы оборудования. Она понижается с увеличением длины частиц корма, их массы, площади кормоотделения, колебаний плотности, влажности и геометрии поперечного среза кормового потока, а также из-за снижения плотности корма и производительности. Это согласуется с данными исследований в области дозированной выдачи измельченных стебельных кормов. Результаты и их обсуждение. Математическое моделирование (24) дозированной выдачи измельченных стебельных кормов показывает, что фракционный состав корма существенно влияет на формирование порции. Различное расположение частиц в пространстве (как в горизонтальном, так и в вертикальном направлениях) при ограничении свободы по горизонтали приводит к отклонению высоты порции. Среднее квадратичное отклонение высоты порции соломы объемом 0,5x0,6x0,01 м, определенное по формуле (18), при длине частиц 39 мм и плотности 25,5 кг/м3 составляет 0,023 м (масса порции 0,776 кг). Увеличение высоты до 0,15 и 0,20 м привело к повышению среднего квадратичного отклонения высоты порции, соответственно, до 0,031 (1,174 кг) и 0,037 м (1,48 кг), а также к изменению объема порции и, как следствие, ее массы, среднее квадратичное отклонение которых соответственно составило 0,057, 0,934 и 0,123 кг (рисунок 3). Уменьшение длины частиц до 27 мм плотностью 33,03 кг/м3 снижает возможные отклонения расположения частиц в условном пласте порции. Поэтому среднее квадратичное отклонение высоты порции объемом 0,5x0,6x0,01 м снижается до 0,014 м, объема - до 0,0013 м3 и массы - до 0,043 кг. Увеличение массы порции до 1,518 и 1,995 кг за счет высоты порции привело также к повышению среднего квадратичного отклонения массы порции соответственно до 0,071 и 0,096 кг. Моделирование процесса формирования порции измельченного стебельного корма свидетельствует о влиянии фракционного состава корма на равномерность выдачи. Адекватность разработанной модели влияния фракционного состава измельченного стебельного корма и его физикомеханических свойств на равномерность выдачи подтверждают полученные экспериментальные данные, где влияние фракционного состава корма определялось экспериментальными исследованиями. --теоретические данные, ----экспериментальные данные Рисунок 3 - Зависимость среднего квадратичного отклонения массы порции от ее величины ----9=205.5 кг/м3, 0=1,0кг/с Рисунок 4 - Зависимость отклонения массы порции от площади кормоотделения при разной плотности корма (/Ср — 22,8 мм) При заполнении емкости шириной 0,6 м и длиной 0,5 м соломой средней длиной частиц 39 мм на высоту 0,10 м среднее квадратичное отклонение массы порции составило 0,079 кг при среднем значении массы порции 0,76 кг (рисунок 3). Увеличение массы порции до 1,154 кг повысило ее среднее квадратичное отклонение до 0,112 кг, а при массе 1,449 кг оно составило 0,130 кг. Уменьшение средней длины частиц до 27 мм также снизило величину отклонения массы порции до 0,042 кг при массе порции 0,96 кг; до 0,070 кг при 1,477 кг и до 0,092 кг при массе порции 1,956 кг. Выводы. Отклонение теоретических и экспериментальных данных в среднем составляет 9,57%, что позволяет утверждать, что математическая модель описывает влияние фракционного состава измельченного стебельного корма на равномерность его выдачи с достаточной достоверностью.
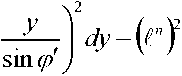
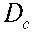
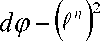
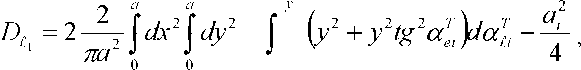
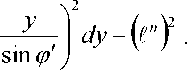
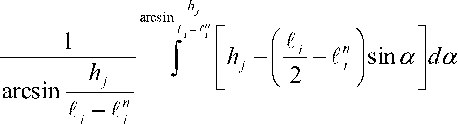
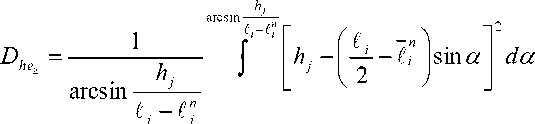
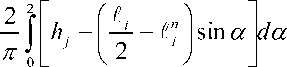
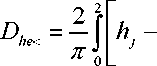
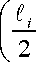
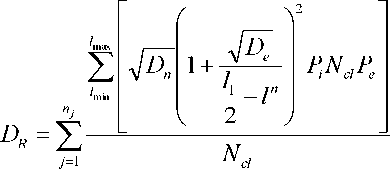
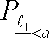
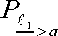
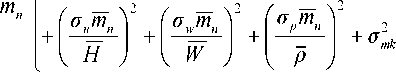
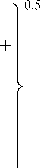
Список литературы Моделирование процесса дозированной выдачи измельченных стебельных кормов
- Система ведения животноводства Ростовской области на 2014-2020 годы. -Ростов-на-Дону, 2013. -498 с.
- Модульная ферма с низкозатратной экологически чистой технологией производства молока: монография/Э.И. Липкович, А.М. Бондаренко, И.Н. Краснов и др. -Зерноград: АЧГАА, 2010. -191 с.
- Краснов, И.Н. Модель оптимизации технологических процессов приготовления кормов как подсистема обеспечения качества/И.Н. Краснов, А.Н. Глобин//Научная мысль. -2015. -№ 3. -С. 243-248.
- Глобин, А.Н. Комплексный показатель качества выполнения технологических процессов/А.Н. Глобин, А.В. Куриленко//Научная мысль. -2015. -№ 3. -С. 278-281.
- Шацкий, В.В. Совершенствование технологического процесса дозированной выдачи измельченных стебельчатых кормов и обоснование параметров питателя-дозатора: диссертация кандидата технических наук/В.В. Шацкий. -Саратов, 1984. -176 с.
- Черкун, В.Я. Исследование технологического процесса приготовления полнорационных кормосмесей крупному рогатому скоту: диссертация кандидата технических наук/В.Я. Черкун. -Запорожье, 1976. -207 с.
- Глобин, А.Н. Дозаторы: монография/А.Н. Глобин, И.Н. Краснов. -Москва -Берлин: Директ-Медиа, 2016. -384 с.
- Глобин, А.Н. Исследование процесса дозирования при приготовлении кормов для сельскохозяйственных животных/А.Н. Глобин, С.К. Оганесян//Современная техника и технологии. -2015. -№ 9.
- Глобин, А.Н. Исследование процесса дозирования при переработке сельскохозяйственного сырья/А.Н. Глобин, А.В. Рясный//Донская аграрная научно-практическая конференция «Инновационные пути развития агропромышленного комплекса: задачи и перспективы». Секция «Инновационные технологии в области хранения и переработки продукции сельскохозяйственного производства»: Международный сборник научных трудов. -Зерноград: ФГБОУ ВПО АЧГАА, 2012. -С. 93-95.
- Василенко, П.М. Механизация и автоматизация процессов приготовления и дозирования кормов/П.М. Василенко, И.И. Василенко; Всесоюз. акад. с.-х. наук им. В.И. Ленина. -Москва: Агропромиздат, 1985. -224 с.
- Методика статистической обработки эмпирических данных. -Москва: Изд-во Комитета стандартов мер и измерительных приборов при Совете Министров СССР, 1966. -100 с.
- Национальный стандарт Российской Федерации ГОСТ Р ИСО/ТО 10017-2005. Статистические методы. Руководство по применению в соответствии с ГОСТ Р ИСО 9001. -Москва, 2005.
- Гмурман, В.Э. Теория вероятностей и математическая статистика/В.Э. Гмурман. -Москва: Высшая школа, 1972. -368 с.
- Вентцель, Э.С. Теория вероятностей/Э.С. Вентцель, Л.А. Овчаров. -2-е изд. -Москва: Наука, 1973. -368 с.
- Гнеденко, Б.В. Курс теории вероятностей/Б.В. Гнеденко. -3-е изд., перераб. -Москва: Физматгиз, 1961. -408 с.


