Моделирование процесса и режимов конвективной сушки зерна
Автор: Авдеев А.В., Начинов Д.С., Начинова А.А.
Журнал: Вестник аграрной науки @vestnikogau
Рубрика: Послеуборочная обработка продукции растениеводства
Статья в выпуске: 1 (16), 2009 года.
Бесплатный доступ
Изложена методика аналитического моделирования конвективного процесса сушки зерна в промышленных зерносушилках при подводе агента сушки в неподвижный и гравитационно перемещаемый слой. Приведена номограмма выбора режимов сушки зерна в зависимости от его назначения и состояния слоя.
Короткий адрес: https://sciup.org/147123366
IDR: 147123366 | УДК: 631.55
Текст научной статьи Моделирование процесса и режимов конвективной сушки зерна
ОАО ВИСХОМ
М ОДЕЛИРОВАНИЕ ПРОЦЕССА И РЕЖ ИМ ОВ КОНВЕКТИВНОЙ СУШ КИ ЗЕРНА
Изложена методика аналитического моделирования конвективного процесса сушки зерна в промышленных зерносушилках при подводе агента сушки в неподвижный и гравитационно перемещаемый слой. Приведена номограмма выбора режимов сушки зерна в зависимости от его назначения и состояния слоя.
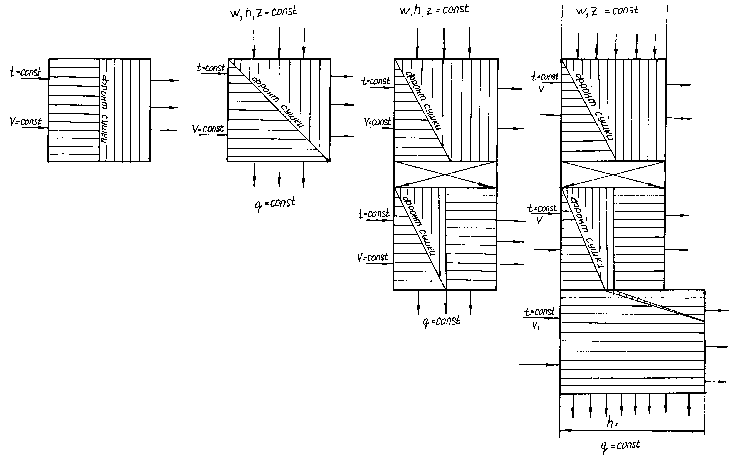
Анализ известных технических средств для конвективной сушки зерна показывает, что в них используются в основном четыре технологические схемы формирования прохождения фронта сушки в слое зерна (см. рис. 1). Так, в неподвижном или горизонтально перемещаемом слое зерна без ворошения (см. рис. 1а), перемещение фронта сушки остается постоянным по толщине слоя. При постоянной толщины положение фронта сушки изменяется и располагается под некоторым углом (см. рис. 1б) к горизонтальной плоскости, относительно которой перемещаются зерновки. В свое время выпускались конструкции зерносушилок и с переменной по высоте сушильной камеры толщиной зернового слоя. В последнее время на рынке сушильной техники они не рекламируются.
установившемся гравитационном движении слоя зерна
б
а
в
г
Зерно: – сухое; [ТТТТТШ – влажное; а – неподвижный слой. Гравитационно перемещаемый : б – слой постоянной толщины; в – с перераспределением потоков, слой постоянной толщины; г – с перераспределением потоков и слоем переменной толщины. W – влажность зерна; Z – высота сушильной камеры; h и h1 – толщина слоя; t – температура агента сушки; V и V1 – скорость агента сушки; q – производительность (пропускная способность); V>V1; h
Рисунок 1 – Схемы прохождения фронта сушки в слое зерна конвективных зерносушилок
В случае перераспределения потоков зерна в сушильной камере (см. рис. 1в), каждая из частей слоя, если он разделен, например, симметрично, находится в зоне максимального нагрева вдвое меньше времени, чем при сушке по схеме б, если высушивается материал того же объема и толщины . Это позволяет предположить, что в таком варианте сушки процесс можно осуществить с гарантией сохранности качества высушенного материала. Сочетание схем (см. рис. 1б и рис. 1в), при использовании согласно первой более толстого слоя (h1), расположенного под тонким слоем (h), позволяет получить конструкцию зерносушилки, гарантирующую практически на выходе зерно однородное по качеству и термо-физическим свойствам (см. рис. 1г). В этом случае положительные технологические решения схемы рисунок 1в дополнительно улучшаются перераспределением зерна в более толстый слой (h1) в нижней части сушильной камеры. Это перераспределение перемешивает зерно, что практически исключает в таком слое фронт сушки, снижает скорость прохождения сушильного агента через слой, за счет увеличения сопротивления последнего, и уменьшает влияние температуры агента сушки на досушиваемый в толстом слое материал, способствуя энергосбережению на процесс сушки за счет аккумулирования тепла в зерне, полученного в тонком слое (h). Расчетами определено [3], что фронт сушки Vф семян в толстом слое можно зафиксировать, как границу между сырыми и кондиционными зернами толщиной в элементарный слой, равный толщине одной зерновки, в котором имеют место зерна кондиционной и несколько повышенной влажности.
Согласно изложенного, для сушки элементарного слоя зерна была сформулирована следующая математическая модель 1
DW = - K e W 9 ;
D e =-- r— KBW 9 - f- КС (1 + K U KBW ff ) ■ (T - e ); (1)
100 C в p a a в
Г .
DT = —— ■ a ( T - e );
ep c г
Дw = ^KWe, l ерг e где p и рг - соответственно, плотность абсолютного сырого зерна и сушильного агента; r - удельная теплота парообразования воды при нормальных условиях (температура 373,15 К; давление 101, 325 кПа);
8 - скважность (порозность) зернового слоя; C и C г -соответственно удельная теплоемкость зерна и изохорическая сушильного агента (изменяется незначительно); а - коэффициент теплообмена, приведенный к единице массы и активной поверхности зерновки (изменяется в широких пределах);
f ~ (1 - е )
R
удельная поверхность зерновки, омываемая сушильным агентом и зависящая от агрегатного состояния высушиваемого слоя; т = 1, 2, 3 - коэффициент конфигурации зерновки, соответственно плоская, цилиндрическая (элипсная) и шаровая; R1 -половина наибольшего линейного размера зерновки; W - влажность зерна; 6 - температура зерна; Т и D -соответственно температура и влагосодержание сушильного агента; KCc и КД - модельные коэффициенты теплообмена; Кв - модельный коэффициент массообмена; К - коэффициент пропорциональности.
Здесь Wp - равновесная влажность зерна; Vz - скорость сушильного агента; ф 0 - относительная влажность отработанного агента сушки; t - время; £ - рассогласование, имеющее характер «белого шума», - случайная функция аргумента W, значения которой равномерно распределены в интервале (0; 1); - = [Wmax (t) - Wmin(t)] - среднее °'t) 3
квадратичное отклонение влажности зерна в слое толщиной H (при принятии гипотезы о нормальном законе распределения данной случайной величины).
При составлении математической модели сушильной установки периодического (циклического) действия (см. рис. 1а) учитывались и другие методы их формирования (равновесные модели, логарифмические модели, высокотемпературная модель сушки зерна применительно к низкотемпературной), которые были получены и другими исследователями (А.С. Гинзбургом, А.И. Анискиным, Г.С. Окунем, В.И. Алейниковым, В.А. Резчиковым, В.С. Уколовым). В модели (2) отражены как основа две стороны: использование концепции обобщенного процесса сушки в типовых (штатных) слоях (с выявлением сходства и различия между ними) и учет равновесных явлений (большая зависимость от физических параметров и внешних условий).
Проведенный анализ и аналитические исследования систем уравнений (1) и (2) позволили разработать математическую модель сушильной установки, работающей с плотным малоподвижным слоем зерна постоянного сечения по высоте сушильной камеры (см. рис. 1б). Эта модель
Система уравнений (1) дополнена краевыми
описывается системой уравнений
условиями, тип которых соответствует коду оператора Д , задающему обыкновенное дифференциальное уравнение, дифференциальное уравнение переноса (субстанциональная производная), дифференциальное
уравнение в частных производных, стохастическое дифференциальное уравнение И то. При этом начальные условия отражают характер изменения W и 6 на входе в изучаемую зону сушильной камеры (постоянная функция времени, случайные функции времени), а пограничные условия - характер теплообмена в
пограничном слое (первого, второго, третьего рода).
Исходя из системы уравнений (1) для сушки элементарного слоя, была получена математическая модель сушильной камеры, работающей при сушке неподвижного слоя зерна (см. рис. 1а)
DM = - K p 0o[W ( x ; t ) - W p ( t )] + KT + — ( , ) ■ M x );
d t (2)
<
DD = ■ К в [ W ( x ; t ) - W p ( t )]; D ( x ;0) = D ,/ x );
∂ t ερ гVг β ρ
W ( t ) = а ф 0( t ) + в ; p 0 = p ( D ; T 0); W ( x ;0) = W 0( x ) + ^ ( & r, x );
t e [0;T; x e [0; H ].
dW HK β
-
-
dx Vh
( w - W k ) ■ ( e - e 0);
d θ dx
-
rHK c в ■ we —а (1+KUK«we) ■ (т - e);
100 С Vh V “ в (3)
dT m ( 1 - е ) C
=- dx RVг Сг
■ кс а (1 + K U K e w e ) ■ ( t - e );
dD dx
- 10 p ( 1 - £ ) K p
ρ г V г
( W - W k ) ■ ( e - e 0);
W (0) = W o; e (0) = e 0; T (0) = T o; D (0) = D 0.
Здесь W к - конечная влажность зерна; V и V г -соответственно, скорости движения зерна и сушильного агента.
Полагая, что процесс работы сушильных камер с переменной по высоте толщиной зернового слоя, например ( h 1 ; h2 ; h3 ), продуваемого агентом сушки, границы которых находятся, соответственно, по высоте L j ,L j +L2,L j +L2+L3 , для такой сушильной камеры была получена математическая модель, описываемая дифференциальными уравнениями вида
LK
— = - ( W - wt ) • ( e - ea );
dx hv
—= ——— к W e - —(i + к и к W e ) • ( t - e );
dx 100С vh e 11 v 111 1
. dT = - m ( 1 - 6 C • Kc (1 + k u kw a ) • ( T - e );
dx RVгCг a 111 1
dD 10p(1 - 6) к, ,.
-D =-- / в W - W k ) • ( e - 9 o );i = 1,2,3;х e ( 0; H ) ;
dx р г V г
W 1 ( / 1 - 1 ) = W - 1 ( I 1 ) ; 6 ( i 1 - 1 ) = e - 1 ( I 1 ) ; W (х)=^ 6 (0) = e 0;
. T ( / 1 - 1 ) = To; D 1 ( l 1 _ i) = D 0 ; / 0 = 0; / 3 = H .
В случае наличия по высоте сушильной камеры H механического перемешивания зерна, например на уровнях l1=L , l2=L1+L2, l3 в этих точках необходимо принимать во внимание влияние диффузии. При решении численным методом на ЭВМ в точках /1 = /1, /2 = /2, /3 = H • q, к правым частям первых двух уравнений систем (3) для рис. 1в и (4) для рис. 1г, соответственно, прибавляется конечноразностная аппроксимация в виде выражений к б dW ~ 4- W /+q)-2W /)+w (•‘ - q)];
dx q кб "ГТ--б V6^ + q)- ^(l)+ 9^1 - q)]; 1 =1,2,3.
dx q
Модельный коэффициент Kб(0≤Кб<1) зависит от степени перемешивания слоя зерна. Ш аг q выбирается исходя на устойчивости разностной схемы (при решении методом Рунге-Кутта устанавливается автоматически). Если обозначить xк + 1 - число пропусков высушиваемого материала Η через сушильные камеры, то получается экспозиции сушки т = хк. Для заданных значений W0, 90 и l = H, v 3
– 1,3 решается задача нахождения значений h ' , минимизирующих функционал
Ф( W,9,T,D ,h i )= x к ; x к :W(x к )=W к ; h^argmmXк, где W, θ , T, D связаны соотношением (4) при системе ограничений:
θ0 ≤ θ ≤ θдоп.; θ0 ≤ T0 ≤ Tmax; dW доп.
dx
.
Для решения системы уравнений была составлена Фортран-программа для ОС ЕС ЭВМ. На ее основе с соответствующими изменениями и добавлениями построена программа для решения системы (4). Указанные программы реализует численный метод Рунге-Кутта 4-го порядка решения обыкновенных дифференциальных уравнений при использовании стандартной процедуры RKGS Минского материального обеспечения.
В результате решения задачи об оптимизации конструкций газораспределителей сушильных установок, с учетом неравенства Коши-Буняковского была получена зависимость для определения оптимальной толщины слоя зерна продуваемого агентом сушки lт= argm n S1 S2, (5)
где S1 и S2 – соответственно, газовое сопротивление газораспределителя и зернового слоя. При этом принято, что
S1 + S2=const ; S2 ≥ S1 >0 (6)
Ф = S 1 S 2 =
2K 1 K3K4C 1 угQ2£ vСр ------------------------------------------------------------------------•------------ ngK2 к6 pd пр a lт
где С1 – коэффициент сопротивления; ξ1 – коэффициент местных сопротивлений; γг – объемная масса газа; Vср – средняя скорость газа через слой зерна; К1, К2, К2, К4, К6 – коэффициенты; n – показатель степени; dпр – приведенный диметр зерновки; a – ширина распределительной поверхности, подводящей газ к слою; p - коэффициент абсолютной вязкости газа; g – ускорение силы тяжести; Q – расход газа; lт – траектория движения газа в слое зерна.
Функционал Ф ( l т ) при фиксированных значениях параметров имеет вод гиперболы. Из системы ограничений (6) и теоремы о постоянной сумме следует, что значение l т ограничено как сверху, так и снизу, т.е.
3 L ; l 1 e [ L ; L 1 ] ; L > 0.
l т
Величина /оп, т ^ L определена из условий L 1 >= L 1 ,
L > L 1 = д р - s * >^ д р , s * = CfS • При этом
S 2 получено выражение
/ опт = L = K 2 K 4 П прДP , (8)
т 4 4 K 1 K 3 C1 p Vc P ^ 1
где ДР - общие потери давления в аэродинамической системе зерносушилки.
Зависимость (8) позволяет определить длину (толщину) слоя, а также подтвердить незначительность (в пределах скоростей фильтрации газа через зерновой слой 0,1…1,5 м/с) суммарных потерь давления в общей аэродинамической системе зерносушильной установки.
Разработанные математические модели сушильных камер для неподвижного и непрерывно перемещаемого в них зерна позволили при расчете внутреннего и внешнего диаметра цилиндрических бункерных коаксиальных зерносушилок, при р1=R
соотношении
, где R и r1 – соответственно, радиусы внешнего и внутреннего цилиндров, из условия потерь энергии с недоиспользованием агента сушки получить два уравнения. Первое, на основании работ А.Г. Кусова [2], для установок, работающих с подвижным слоем постоянной толщины по высоте сушильной камеры
P <, 1 +----- Ko------ n +.1)
pm P (W - W o )e0
^^^^^в
радиусов от внутреннего цилиндра и проходящего через середину слоя ( R о ); W 1 , W р , W m – соответственно, начальная, равновесная и фактическая в поясе m влажность зерна; n , A , В – эмпирические коэффициенты; qm – расход газа через m – пояс; εо – порозность слоя. Уравнение (9) и (10) могут решаться графически или путем численного подбора на ЭВМ.
Нашими исследованиями определено, что эффективная работа сушильных установок во многом зависит от уровня потерь энергии в них, которая хорошо аппроксимируется температурой, выходящей из сушильной камеры паровоздушной смеси (Тс). На основании массового баланса расходов поступающего в сушильную камеру агента сушки и уходящего из нее отработанной паровоздушной смеси получено уравнение
GзТ 2QaQ^ + G c ( A - 1) —Qc- = 0, (11)
aн a a cв B' cвТнВ'
где A '= 1 - [ 1 - Ьк ). Ьк ;
l be J Pn
L щ от ;
/2 2
щ от с= 7,2 -105 ■ g^H ■ 273/о;
т _ А-сТ •
Т = ------ 9------ ;
в с'-Ga' ВТ a 1н
S i = 4+
1 f щ 2
L om Th ■ ;
от / ух
b n и цв - молекулярная масса пара и воздуха; рn и р б -парциональное и барометрическое давление паровоздушной смеси внутри конфузора; G a и Q a – массовый часовой расход и количество тепла, подаваемые в сушильные камеры; св – теплоемкость воздуха; Тв и Тн – абсолютные температуры, паровоздушной уходящей смеси и наружного воздуха; H1 – расстояние между отверстиями подсасывающих воздух щелей и вытяжкой конфузора; γв , γн , γух – объемная масса, соответственно, наружного воздуха, в диффузоре и уходящей паровоздушной смеси; ξщ и ξот – коэффициент местных сопротивлений подсасывающих воздух щелей и вытяжного отверстия конфузора; γо – удельная масса сухого воздуха; f щ , f от – площади щелей подсоса воздуха и вытяжного отверстия конфузора; g – ускорение силы тяжести.
Применение на практике выше изложенных математических моделей затруднительно и продолжительно во времени. Это связано со значительным количеством математических выкладок и необходимостью определения экспериментальным путем большого количества эмпирических коэффициентов, учитывающих влияние различных факторов на процесс сушки зерна. Поэтому был разработан [1] упрощенный метод расчета с использованием нескольких математических зависимостей и номограмм. В разработанном методе принято, что производительность зерносушилки обратно пропорциональна величине скорости сушки N о , которую можно представить зависимостью:
N = 100L(J 1 - Jо), %/ч, (12) qТ где qT – удельный расход тепла при 100% насыщении агента сушки влагой, ккал/кг; L – удельный расход сухого воздуха на 1 кг сухой массы, кг/кг∙ч; J0 и J1 – теплосодержание агента сушки до и после прохождения зерновой массы, ккал/кг, где L есть:
L _ 3600yvF , кг/кг^ч (13)
G сух здесь F – площадь подвода сушильного агента в зерновую массу, м3; Gcyx – сухая масса материала, кг; γv – массовая скорость сушильного агента в пересчете на сухой воздух, кг/м2 с.
В работе [4] рассмотрены возможные расходы тепла в теоретической сушилке (100% насыщение агента сушки) в зависимости от параметров процесса сушки (см. рис. 2). Из графических зависимостей видно, что в диапазоне температур сушильного агента t=70…150°С величина qT изменяется в пределах от 740 до 810 ккал на кг испаренной влаги, т.е. менее чем на 10%. Отсюда сделан вывод, что производительность сушилки в основном зависит от величины qT, входящей в числитель выражения (12), и пропорционально интенсивности теплоснабжения слоя Q:
Q _ L ( J 1 - J 0 ) , кКал/кг-ч, (14) увеличение, которой может быть достигнуто путем повышения удельной подачи или температуры
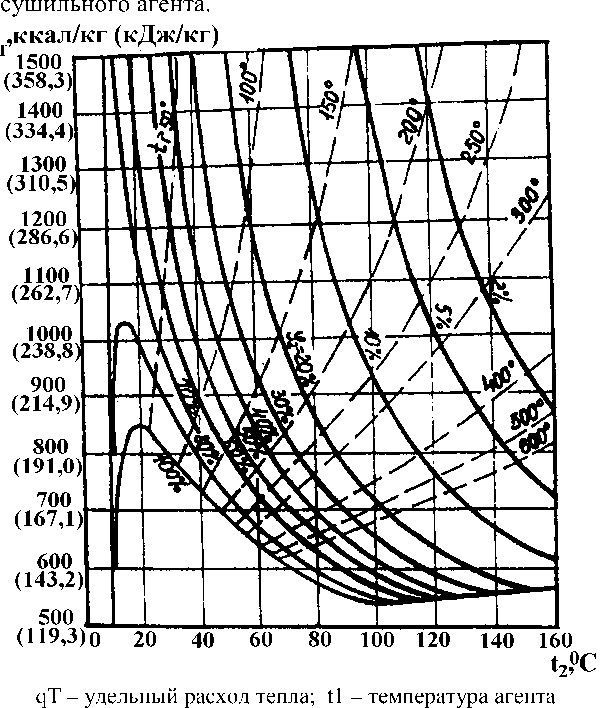
сушки; t2 – температура отработанного агента сушки; φ2 – влагонасыщение отработанного агента сушки
Рисунок 2 – Зависимость удельного расхода тепла в теоретической сушилке от параметров процесса сушки (по Ю.Л. Фрегеру [4])
Зависимости (12), (13) и (14) были положены в основу номограммы для определения эффективных режимов работы сушилки. При этом зависимости удельного расхода тепла q r =f(t 1 ) и времени сушки τ =f(t1) от температуры теплоносителя (агента сушки), при сушке зерна с 25 до 15%, получены с помощью графических зависимостей (по Ю.Л. Фрегеру)
удельного расхода тепла и экспозиции от параметров процесса сушки. Ограничения предельно допустимых температур нагрева зерна от времени сушки θ 3 доп =f( τ ) при его влажности 15, 25 и 35% рассчитывалось по известной формуле С.Д. Птицына:
^ 3 доп
0,37 ( 100 - № н ) +W н
+ 20 - 10 l дт,
оС,
где WH – средняя начальная влажность зерна, %; τ – экспозиция (время) сушки, мин.
Удельный расход тепла, цтккал/кг
900 1000 1100 1200 1300 1400 1500 1600
и 1375 15201580
Время сушки, минт
Ограничения предельно допустимых температур ^З ^ 25
нагрева зерна: Здоп – при влажности зерна 15%; Здоп – ^ 35
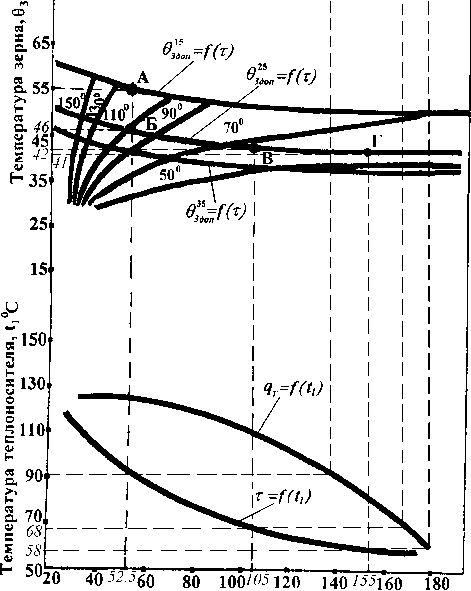
при влажности зерна 25%; Здоп– при влажности зерна 35%. т. А – предельно допустимая температура нагрева зерна при влажности 15%. Исходные точки для определения терморежимов: т.Б – для продовольственного зерна в вертикально перемещаемом слое (Wн=25%); т.В – для семенного зерна в вертикально перемещаемом слое (Wн=25%); т.Г – при сушке зерна в плотном неподвижном слое (Wн=25%)
Рисунок 3 – Номограмма определения эффективного режима сушки зерна в плотном неподвижном и вертикально перемещаемом слоях
Все выше изложенное позволило разработать номограмму (см. рис. 3) для определения терморежимов сушки зерна повышенной влажности для слоев гравитационно перемещаемого и неподвижного. Пользование номограммой заключается в следующем . В начале задаются предельно
допустимой температурой нагрева сухого зерна θ3., проекция значения которой на кривую в15 позволяет нам получить т.А. Пересечение вертикали из т.А. с кривой 0ЗД дает значение предельно допустимого нагрева зерна влажностью 25%. Пересечение той же вертикали с зависимостью τ=f(t1) позволяет определить время сушки τ и температуру теплоносителя t1, проекция значения которой на кривую qr =f(t1) дает возможность определить удельный расход тепла qT. При этом определены следующие значения терморежимов сушки зерна исходной влажностью 25%: для вертикально перемещаемого слоя зерна продовольственного назначения температура агента сушки должна составлять 90°С, экспозиция сушки 52,5 мин. и удельный расход тепла 1 375 ккал/кг при допустимой температуре нагрева зерна 46°С; для вертикально перемещаемого слоя зерна семенного назначения эти показатели соответственно должны быть 68°С, 105 мин., 1520 ккал/кг и 42°С; при сушке зерна в плотном неподвижном слое: 58°С, 155 мин., 1580 ккал/кг и 41°С.
Таким образом, математическое моделирование конвективной сушки зерна для промышленных зерносушилок позволяет проследить сам процесс сушки, связанный с многочисленными факторами и параметрами, а также оценить их влияние на удаление влаги из зерна. Выбор же режимов сушки по номограмме обеспечивает гарантированную сохранность качественных показателей зерна в зависимости от его назначения. При этом определяются и теплозатраты на процесс конвективной сушки.
Список литературы Моделирование процесса и режимов конвективной сушки зерна
- Авдеева, А.А. Обоснование термо-технологических приемов сушки пшеницы на сушилках типа «С» [Текст]: автореф. дис. на соиск. учен. степ. канд. тех. наук/А.А. Авдеева. -М.: ВИСХОМ, 2004.
- Кусов, А.Г. Исследование процесса сушки семян подвергнутых влажному термодинамическому обеззараживанию [Текст]: автореф. на соиск. учен. степ. дис. канд. тех. наук/А.Г. Кусов. -М.: ВИМ, 1971.
- Окунь, Г.С. Расчет продолжительности и энергостойкости процесса сушки зерна в слое с помощью ЭВМ. [Текст]/Г.С. Окунь, И.И. Берман, Ю.В. Есаков//Сб. науч. трудов: Совершенствование послеуборочной обработки зерна в колхозах и в совхозах, т. 100. -М.: ВИМ, 1984. -73 с.
- Фрегер, Ю.Л. Исследование процесса конвективной сушки зерна в виброжиженном слое [Текст]: автореф. дис. на соиск. учен. степ. канд. тех. наук/Ю.Л. Фрегер. -М.: ВИСХОМ, 1986.


