Моделирование процесса интерференции ПЭВ и объемного излучения

МОДЕЛИРОВАНИЕ ПРОЦЕССА ИНТЕРФЕРЕНЦИИ ПЭВ И ОБЪЕМНОГО ИЗЛУЧЕНИЯ

Поверхностная электромагнитная волна (ПЭВ) является чувствительным зондом при исследовании свойств приповерхностных слоев металлов, так как ее амплитуда максимальна на поверхности. Из измерений затухания ПЭВ можно получить коэффициент поглощения в металле [1] и определить мнимую часть комплексного эффективного показателя преломления. Фазовая спектроскопия ПЭВ [2] позволяет определять действительную часть эффективного показателя преломления, используя интерференционные измерения набега фазы поверхностной волны.

Схема эксперимента представлена на рис; 1. Излучение падает на зазор между металлом и экраном, дифрагирует на нем, частично преобразуется в ПЭВ. ПЭВ распространяется по поверхности металла до края и на краю преобразуется в объемную волну, которая интерферирует с волной, дифрагированной на зазоре. Распределение интенсивности интерференционной кар тины регистрируется на линии, перпендикулярной плоскости металла и на некотором расстоянии от края.

Рис. 1, Образование интерференционной картины при апертурном возбуждении ПЭВ

Расчет распределения интенсивности в интерференционной картине был проведен в два этапа. Сначала была рассмотрена задача о распространении ПЭВ и дифрагированного излучения в рамках импедансного приближения над металлом. ПЭВ распространяется по поверхности z = 0, которая характеризуется импедансом

Z = R - IX = /1/е (R,X > 0),                                          (1)

где е - диэлектрическая проницаемость среды.

Рассматривается ТМ - поляризованное монохроматическое излучение с частотой V. Отличными от 0 компонентами являются Н^, Ех, Е^. Задача вычисления поля сводится к определению Н^, а Ех и Ег вычисляются из уравнений Максвелла. ПЭВ возбуждается на зазоре высотой d в плоскости х = 0. Относительно оси у задача трансляционно инвариантна. В области распространения ПЭВ необходимо решить волновое уравнение

□ Н (х, z,t) = 0(2)

с граничным условием Леонтовича [3] для сред с большим е

^ + ikZH = 0 при z=0,(3)

где k = 2rw - волновой вектор.

Начальное условие - возбуждающее поле на щели 0 < z < d

V0(z) = A-lkaz + Be1*02 .(4)

Решение ищется в виде:

H(x,z,t) = V(x,z)elkx”wt.

Тогда уравнение (2) сводится диффузии D = i/2k:

dV _ ^^V граничное условие принимает вид:

-^ + ikZV(x,z) = 0 при z = 0.

(5) к уравнению диффузии с коэффициентом

Формализм решения параболического уравнения (6) подробно описан в монографии [3]. Решение его можно записать в виде:

V(x,z) = Г dz*G(x,z-z¹)Vo(z*), ^00

где

G(x,z-z*) = (-5^) 1 exp

ik (z-z¹)² in

2 x      ~ 4

- функция Грина;

Vo(z') - начальное условие, которое соответствующим образом продол- жено в область z < 0 с учетом граничного условия.

Для начального условия (4) продолженное начальное условие имеет О, z > d вид:

Ae"ikaz + Beikaz         0 < z < d

Vo (2)

. ^a-Z ikaz Oa+Z

Vw e - B5^z

-ikaz , A В . -ikZz

e + 2z<5Sz " S=z’e ' "d<2<0

< 9 >

2Z (А-

^_e~ik(a+Z)d a+Z

. ik(a-Z)d ., „

B———---,----)e'lkZz a—z

Подставив (9)

в (8), получим решение параболического уравнения:

V(x,z) = ^ e

1 o(x+£)2 (

7 e

^T ^²[fte'^2p^ W(p+t-C) + Be^2p^

ве2р^ Ae-2p^

e|— - )2ow(o+t+d - p-о p+o

Ае'2р^ £~ W(-p+T+O - Ве2р£ 2^ Wtp+т+С:

где

1 т® ’

2 е

'Ар+о

^

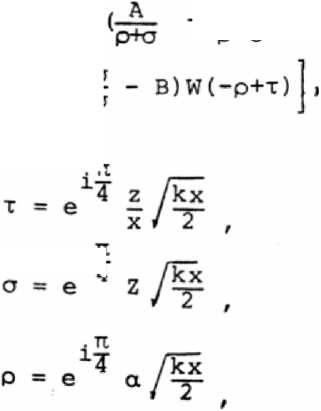
--™)2oW(o+x) + (В2^ - A)W(p+T) + p-о              р-С

£ = е 4

W(E) = еЕ

/п i“

п 2

е dn ~ интегральная функция комплексного аргу-

мента.

Предположим,

что на зазор падает плоская волна, тогда А = 1,

В = 0, а = 0 в (4), а решение можно записать следующим образом:

V(x,z) = |е^(т”^² W(r4) + е^(т+^ ² (~W(o+t+O +

+ 2" W(t+£) + е

Решение (11),

тЗ

(W (о+т) - W (т) ) .

полученное в импедансном приближении, справедливо

для х, удовлетворяющих неравенству

Е2

что в эксперименте хорошо выполняется для металлов (е~10³),   х-10 см

в области

Был

v * 1000 см-1*

проведен модельный расчет поля вблизи поверхности металла для

металла

С У

Р тоты у = 1000 см-1.

см*¹, у = 800

см-1 при зазоре d = 60 мкм для час-

Импеданс металла

вычисляется по

формулам:

х

у

- (1

vt

R

Р

у2

/2 у L v            J

Р Распределение поля, вычисленное

по формуле (11), аналогично распре

делению поля при дифракции Фраунгофера на щели 2d, так что направления на минимумы S^ удовлетворяют условию:

Э1

= ^L 2d

где

1,2

длина волны,

Однако присутствие импедансной плоскости приводит к тому, что нулевой дифракционный максимум разделяется на ПЭВ и "скользящую" объемную волну. Распределения поля вблизи поверхности представлены на рис, 2 для разных расстояний а от возбуждающей диафрагмы. ПЭВ локализована у поверхности металла и затухает, распространяясь вдоль поверхности. Максимум объемного излучения удаляется от поверхности с увеличением расстояния, а минимум, отделяющий его от ПЭВ, находится вблизи поверхности. Если проследить за Фазой ПЭВ, можно заметить, что она отличается от фазы ПЭВ,

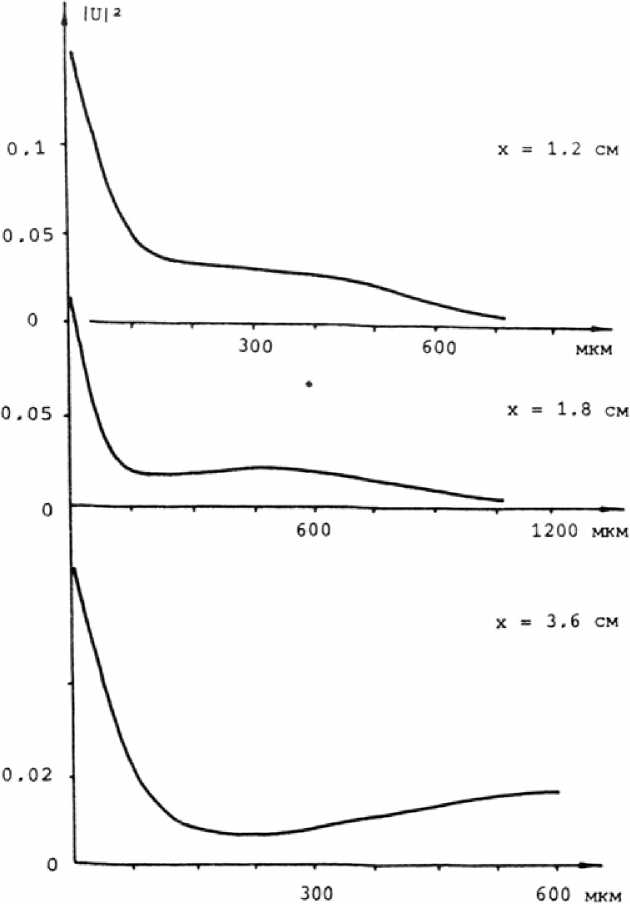
Рис. 2, Распределение интенсивности излучения вблизи поверхности по вертикальной координате для различных расстояний а от возбуждающей щели

распространяющейся по поверхности без влияния на нее объемного дифраги рованного излучения. Это дополнительная фаза определяется размером возбуждающей диафрагмы d, параметрами металла и расстоянием от возбуждающей диафрагмы а. Но ее можно считать постоянной в некотором диапазоне изменения а.

Рассчитав поле на краю образца, можно вычислить распределение интен сивности интерференционной картины на оси z, пользуясь принципом Гюйген са. Поле ищем в виде интеграла Кирхгофа [4]:

Ну(х,z)

где

* Н

1 х4

—— е

8пк

/ de с

ГЭН -1кг

—Z е____

Эп /г

Н

У

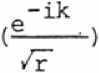
С - контур, охватывающий точку (х, z) ;

г - расстояние от точки до контура.

Выберем контур, проходящий по оси z* и замыкающийся на бесконечности.