Моделирование процесса изнашивания зубьев фрезы на основе термокинетического подхода

комплексом факторов, обусловливающих источники и стоки массы с поверхности трения, связанные с тангенциальным перемещением и деформированием среды; с явлениями диффузии из-за различия концентраций компонентов в различных точках движущейся среды, а также наличия термо- и бародиффузии, с наличием пространственной неоднородности в распреде- лении температуры и переносом теплоты путем теплопроводности, конвекции и излучения, а также с химическими реакциями в зоне трения, с механическим отделением частиц среды и с взаимодействием среды с энергией других видов и др.

В агрегированном виде обобщенная математическая модель износа h_S поверхностей имеет вид [5]:

h = I_hL T

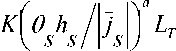
В уравнении (1) I_h = K

[в h jj

V s sj s

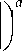
– ин-

тенсивность изнашивания поверхности, определяемая обобщенным безразмерным термокинетическим критерием изнашивания, характеризующим отношение производства энтропии Os в подвергаемом трибо-воздействиям слое hs твердого тела к изменению энтропии в указанном слое за счет переноса ее потоком js ; K, a – соответственно коэффициент про- порциональности и показатель степени, определяемые экспериментально; LT – путь трения.

При адаптации обобщенной модели (1) к конкретному виду трибосопряжения необходимо решить вопрос о том, чтобы выделить ведущие процессы изнашивания, установить основные воздействующие факторы, определя-

Известия Самарского научного центра Российской академии наук, т. 22, № 1, 2020

ющие контактное взаимодействие элементов трибосистемы. Для наглядного представления ее функционирования составляется структурно-функциональная схема трибосистемы (см. рис. 1), на которой приводят все взаимодействующие элементы и параметры.

С учетом вышеизложенного обобщенная математическая модель (1) для рассматриваемого случая изнашивания зубьев фрезы по задней поверхности получена в следующем виде:

a

ГГ                    1_Y a_

h = ^K k ^U s/ h s + Y d T o T g + T i j |^{V T} I h s l\jq\ L T , ⁽²⁾

где t_s и u _S - касательные напряжения и скорость скольжения на задней поверхности зуба фрезы; Y _d , T _a и T . соответственно, коэффициент гистерезисных потерь, тензоры напряжений и скоростей деформации; V T и j q - градиент температуры и плотность потока (поток на единицу площади тепловой энергии), соответственно.

В уравнении (2) первый член показывает потери, связанные со скольжением в пределах площади контакта; второй член уравнения учитывает затраты мощности на деформирование материала контактной поверхности, т.е. с эффектом упругого гистерезиса; третий член связан с наличием пространственной неоднородности в распределении температуры вследствие переноса теплоты; знаменатель соотношения (2) выражает влияние изменения энтропии в поверхностном слое h_s за счет переноса теплоты путём теплопроводности, конвекции и излучения. Все величины, входящие в уравнение (2) в соответствии с рекомендациями [1...5] и др., можно выразить через известные параметры процесса фрезерования и контактного взаимодействия по задней поверхности фрезы с обрабатываемой деталью (см. рис. 1).

Так на основе данных вышеуказанных исследований можно отметить, что для структурнофункциональной схемы контактного взаимодействия при фрезеровании (см. рис. 1) имеют место следующие зависимости общего вида:

• -    касательные напряжения на контактной площадке зуба фрезы

^T s = Ф т ⁽ F N 1 , f_c , L , E i , ^{E , U} J ^;

• -    скорость скольжения 4 =%^{( П}ф , d i , 5 ) ;

• -    толщина слоя h_s на контактной площадке, в которой протекают все те явления и процессы при трении, обуславливающие возникновение термодинамической ситуации, приводящей к изнашиванию;

• -    в соответствии с [4] в первом приближении может быть принята h s = 5 . 10^-3 мм.

Далее, затраты энергии на упругий гистерезис можно определить из условия, что при вращении заготовки относительно контактной площадки зуба фрезы на ней происходит пере-деформирование волн контурной площади контакта A c [7], механизм формирования, которой существенно определяется характеристикой волнистости поверхностей [8,9,10]. С учетом этого можно записать:

Y d T o T e =^{Ф д (} Y ) ’ z c ’ ^Ф т ^ he ’ L ^в’ h s ) ’ где z_c - число волн на поверхности контакта, Ф j - энергия упругой деформации одной волны, to - угловая скорость вращения фрезы, h_c - относительная контурная площадь, L - полудлина упругой площади контакта, в - ширина фрезы.

Плотность потоков j q , входящих в формулу (2) найдем, записав тождество:

L = Ф A а .

q q

Ф_q определяется как Ф_q = Ф_S + Ф_i , где Ф_S - поток, учитывающий энергообмен с окружающей средой, Ф_i - тепловые потоки за счет теплопроводности в контактирующие детали, A - номинальная площадь трения.

Энергообмен с окружающей средой определяется на основании закона Ньютона-Рихмана уравнением

Ф. = аА T j dA ,

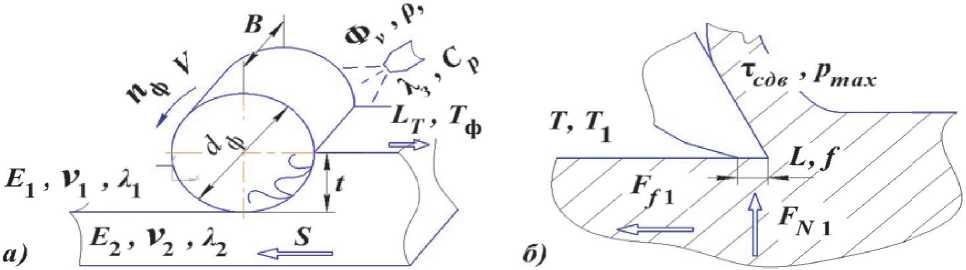
Рис. 1. Структурно-функциональная схема цилиндрического фрезерования - а) и трибосистемы по задней поверхности зубьев фрезы - б)

где а = ф_а ( ^ , п , р , X , C_p , T _Y , T 1 , l ) - коэффициент теплоотдачи; A T = T — T 1 . Тепловые потоки Ф_; с поверхности контакта прилегающей зоны тем можно выразить на основании закона Фурье через коэффициент теплопроводности λ _i , площадь A и температурный градиент Δ T , т.е.

Ф. =-^ A .A T. i ii i

ЗАКЛЮЧЕНИЕ

Таким образом, исходя из изложенных результатов можно констатировать, что полученное уравнение (2) включает в себя практически все элементы и параметры, определяющие комплексное влияние на процесс изнашивания задней поверхности зубьев фрезы при цилиндрическом фрезеровании.