Моделирование процесса экстракции пектиновых веществ из свекловичного жома с применением вибрационного воздействия

В настоящее время одной из острых проблем является проблема создания экологически безопасных пищевых и перерабатывающих производств . В связи с этим возникает задача утилизации отходов . Особенно это касается свеклосахарного производства , в котором вторичные сырьевые ресурсы , в частности , свекловичный жом , составляют 80-83 % к массе переработанной свеклы . Между тем , свекловичный жом является одним из основных источников получения низкометоксилированного пектина , который может быть использован для производства пищевых продуктов и напитков оздоровительного , защитного , лечебного и профилактического назначения .

Для интенсификации процесса извлечения пектиновых веществ из пектиносодержащего раствора существуют различные способы , одним из которых является вибрационное воздействие . Оно позволяет значительно ускорить процессы массообмена , снизить себестоимость и повысить качество получаемого продукта . В некоторых случаях использование вибрации позволяет создавать новые технологические процессы , которые без вибрации были бы нерентабельны .

Основным процессом при получении пектиновых веществ из растительного сырья ( например , свекловичного жома ) является экстракция . В то же время теоретические основы этого процесса в настоящее время изучены недостаточно . Отсутствует комплексная модель процесса , учитывающая как мембранные свойства оболочки растительного сырья , так и возможности управляемой экстракции . Поэтому задача моделирования процесса экстракции пектиновых веществ из свекловичного жома является актуальной . Моделирование процесса экстрагирования позволяет на стадии проектирования изучить данный процесс при тех или иных технологических параметрах , выявить оптимальный закон движения рабочего органа и структуру будущей установки или машины . Это особенно важно в тех случаях , когда технологической обработке подвергаются вещества с новыми свойствами , когда нет ясной картины механизма взаимодействия рабочего органа с обрабатываемой средой .

Изучению процесса экстракции в системе твердое тело - жидкость в пищевой промышленности посвящены работы многих исследователей [1, 2].

The results of the mathematical modeling of the vibroextraction process of the pectin substances from sugar beet pulp are presented in this work.

Основным недостатком этих работ является то , что многие из них являются эмпирическими и экспериментальными , в них рассматриваются отдельно гидродинамические , тепловые и массообменные процессы и не учитывается внешнее ( например , вибрационное ) воздействие . Поэтому необходимо решить комплексную задачу , позволяющую учесть все действующие факторы .

Скорость процесса экстрагирования в системе твердое тело - жидкость зависит от следующих факторов [2]:

• -    величины движущей силы процесса ;

• -    скорости каждой из стадий процесса ( переноса вещества внутри твердой частицы , массоотдачи от поверхности частицы к экстрагенту , набухания частиц , растворения целевого компонента внутри частицы );

• -    размера и формы частиц ;

• -    вида слоя частиц , который они образуют ( подвижный , неподвижный );

• -    соотношения масс экстрагента и твердых частиц ;

• -    характера относительного движения твердых частиц и экстрагента ( противоток , прямоток , рециркуляция жидкости );

• -    температуры ;

• -    скорости движения фаз .

В тех случаях , когда лимитирующей стадией процесса является массоотдача от поверхности частиц к экстрагенту , возникает необходимость применять перемешивание , вибрацию и другие средства , интенсифицирующие массоотдачу .

Материалы и методика исследований

Перенос вещества диффузией и конвекцией описывается с помощью дифференциальных уравнений параболического типа . Общее модельное уравнение диссипации , конвекции и кинетики запишем в виде [3]:

• д и    , д ² и    д и

• —    = d   - a— + bu + f ( t , x ) ,    (1)

dt дx     дx где a, b, d - постоянные коэффициенты (d > 0).

Первое слагаемое в правой части уравнения соответствует переносу вещества диффузией , второе - конвективному переносу , третье - источнику , пропорциональному концентрации ( кинетический член ), четвертое - внешнему источнику .

При массопередаче в системе твердое тело-жидкость скорость процесса в каждый данный момент времени зависит не просто от средней концентрации в твердой частице, но от поля концентраций и характера его изменения в процессе экстракции. Для того чтобы математически описать процесс экстрагирования из твердого тела, необходимо решить дифференциальное уравнение нестационарной диффузии при вибрационном воздействии:

дс дс     дс     дс

— + — V + — V + — V дт д x      д у      д z z

= D

д c д c д c v дХ2+ ду2+ д?,

, (2)

+ a ^ y cos to t

дс где – локальное изменение концентрации;

дт

дс     дс     дс

— Vx + —— Vy + —— Vz - конвективное изменение дx     ду     д z концентрации; D – коэффициент диффузии; а – амплитуда колебаний жидкости; ю - частота колебаний; у - единичный вектор, направленный вертикально вверх.

Для одномерной задачи ( расчетная схема представлена на рисунке 1, где с Т и с Ж – концентрация вещества в твердом теле и в ядре потока жидкости соответственно ) математическую модель запишем следующим образом [4]:

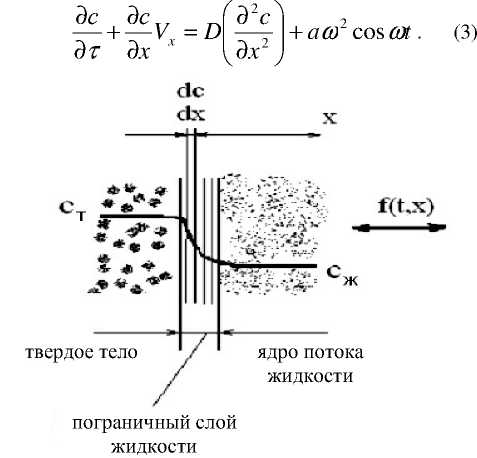
Рисунок 1 – Расчетная схема процесса экстракции

Дополнительно к составленному уравнению :

- граничные условия, зависящие от формы сосуда – непротекание и неприлипание к стенкам сосуда;

- массообмен на границе фаз для системы твердое тело-жидкость, для рассматриваемого случая – это граничные условия третьего рода [2]:

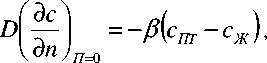
где в - коэффициент массоотдачи; сП T - концентрация экстрагента в жидкой фазе; п – направление, нормальное к элементу поверхности;

• -    геометрические условия однозначности , то есть известны форма и размеры частиц ;

• -    физические условия однозначности , характеризующие физические и диффузионные свойства сред , участвующих в процессе ( коэффициент диффузии , плотность жидкости , ее кинематическая вязкость );

• -    начальные условия ( при т = 0) - начальная скорость V 0 (x,y,z,t) = 0, начальная концентрация в растворе ( жидкой фазе ) С 0 Ж = 0, в веществе ( твердой фазе ) – С 0 Т = С MAX . Т = const, на входе в слой физические свойства растворителя постоянные .

Представленная математическая модель , описывающая процесс виброэкстракции, позволяет провести теоретические исследования в данной области и затем сравнить их с экспериментальными данными, что будет являться новым подходом в решении задачи, поскольку предыдущие исследования базировались , в основном, на экспериментальных работах и эмпирических зависимостях.

Результаты и их обсуждение

При численном моделировании и решении задач механики сплошной среды применяются методы конечных разностей и конечных элементов . Анализ различных численных методов показывает , что наиболее подходящим , обеспечивающим устойчивый счет , является метод крупных частиц ( МКЧ ) [5]. Основная идея метода состоит в расщеплении по физическим процессам исходной нестационарной системы уравнений , записанных в форме законов сохранения . Стационарное решение задачи , если оно существует , получается путем расчета переходного режима системы из начальных условий при многократном повторении вычислений по времени . МКЧ позволяет осуществить численный эксперимент , который занимает сравнительно небольшое время на ЭВМ , обеспечивает устойчивый счет . Среда здесь моделируется системой из жидких ( крупных ) частиц , совпадающих в данный момент времени с ячейкой эйлеровой сетки .

Исходными данными являются реологические параметры твердого тела ( материала ), параметры вибрации ( частота f и уровень вибрационного

^^л ускорения Г — —), геометрические размеры сосуда, g его форма, начальное расположение материала, его начальная скорость и концентрация целевого вещества. Для описания начального расположения материала в момент времени t=0 значение концентрации в соответствующих крупных частицах приравнивается к некоторому значению Сн.

При изучении динамики процесса экстрагирования были рассмотрены гармонический и полигармонический законы изменения вибрационного ускорения , для которых выполняется условие :

концентрация на поверхности твердого тела ; с Ж –

Т

J ^ ( t ) dt = 0; L. - L = 2 Е ,     (5)

где ^ - вибрационное ускорение ; Е - постоянная ; Т – период вибрационного действия .

Для визуализации полученных результатов использовался пакет программ , разработанных на кафедре теоретической механики и мехатроники Ю го - Западного государственного университета . Разработанная методика позволяет исследовать поведение жидкой среды при вибрации , получить эпюры изменения концентрации , проекций скоростей , которые дают возможность исследовать особенности процесса экстрагирования при различных условиях . Задача решалась в безразмерном виде , чтобы иметь возможность интерпретировать результат для различных конфигураций экстракторов и различных исходных твердых тел .

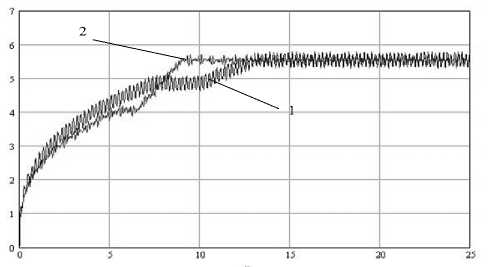
Рисунок 2 – Изменение концентрации пектиновых веществ с течением времени (Δ t =0,0001):

1 – гармоническое воздействие; 2 – полигармоническое воздействие

Для проверки адекватности математической модели процесса экстракции, описываемой уравнениями (3), была проведена серия численных расчетов. Определялась концентрация пектиновых веществ в растворе в зависимости от продолжительности процесса. На рисунке 2 приведен график зависимости изменения величины к о н ц е н т р а ц и и п е к т и н о вых веществ в растворе с течением времени при гармоническом и полигармоническом воздействии на рабочую среду.

Выводы

Проведенное моделирование показало , что вибрационной воздействие интенсифицирует процесс экстракции пектиновых веществ из свекловичного жома , а также то , что на скорость изменения концентрации пектиновых веществ в экстракте влияет вид вибрационного нагружения , его параметры и реологические характеристики обрабатываемой среды .

Работа выполнялась в рамках федеральной целевой программы « Научные и научно - педагогические кадры инновационной России » и была поддерж ана Госконтрактом № П 1576 от 10.09.2009 г .