Моделирование процесса электрохимической размерной обработки катодом, совершающим колебательное и вибрационное движения

Экспериментально установлено, что осуществление дискретизации процесса растворения при электрохимической обработке (ЭХО) улучшает точностные показатели [1]. В работе [2] приведена ЭХО длинномерных труб. На боковой поверхности катода нанесены полосы из изолирующего материала (фторопласта). Разрыв процедуры электрохимического растворения в рассматриваемой модели осуществляется при следующих условиях: катод неподвижен, анод вращается, анод неподвижен, катод вращается. В каждом случае любой локальный участок обрабатываемой детали то закрывается от потока электрического тока изолирующей полосой, то остается открытым для электрического потока. Длительность паузы должна быть такой, чтобы производилась полная релаксация электролита, что достигается увеличением размера изоляционных полос или изменением их количества. И этот процесс повторяется циклически.

Дискретное прерывание электрохимической обработки можно также осуществить, если обработку вести в импульсном режиме.

Высокая точность копирования достигается и за счет того, что электроду сообщается колебательное движение в направлении подачи, синхронизированное с импульсами технологического напряжения. При этом важным параметром, влияющим на точность и производительность обработки, является выбор момента подачи импульсов напряжения относительно контактирования электродов. При подаче импульса напряжения, в момент максимального зазора, величина тока сравнительно невелика, поэтому скорость растворения анода также невелика. Подача при расхождении электродов ведет к повышению плотности тока, но деталь в этом случае имеет низкую шероховатость обработанной поверхности (рябь, неравномерное растворение). Вероятно это вызвано растворением анода в условиях пониженного давления электролита в зазоре, плохим его заполнением и интенсивным закипанием. При подаче импульсов в момент сближения электродов с прекращением напряжения в момент контактирования наблюдается максимальная точность и минимальная шероховатость, что можно объяснить равномерным заполнением зазора и повышенным давлением электролита. Этот способ в практике ЭХО более предпочтителен и реализован во многих импульсно-циклических схемах.

Авторы работы [3] всесторонне изучали влияние вибрации на точность копирования и пришли к выводу, что основное влияние на точность копирования оказывает не столько импульсный ток, сколько вибрация катода-инструмента (при условии, что вибрация электрода формирует межэлектродный зазор (МЭЗ)).

Расчетная схема, рассмотренная в данной работе, представлена на рис. 1. Катод-инструмент вращается вокруг гео метрической оси равномерно, делая п оборотов в минуту, и совершает вибрацию вдоль этой оси с частотой/[3].

Рис. 1. Схема процесса ВЭХХ. 1 - обрабатываемая деталь;

2 - катод-инструмент; 3 - токопроводящий защитный слой;

4 - изолятор; 5 - токопроводящие абразивные сектора;

6 - межэлектродный зазор; 7 - технологический межэлектродный зазор

Предлагается следующая физическая модель процесса обработки детали в кольцевом МЭЗ:

• -    выделение водорода на катоде и растворение металла на аноде подчиняются закону Фарадея;

• -    приэлектродные зоны не оказывают существенного влияния на электропроводность электродной среды;

• -    газовые пузырьки равномерно распределены по кольцам постоянного радиуса и неравномерно по его длине;

• -    напряжение постоянно во всех точках поверхностей электродов;

• -    плотность тока постоянна в точках кольца постоянного радиуса и изменяется с менением положения точки на радиусе;

• -    электролит нагревается только от выделения Джоулева тепла.

Водород, выделяющийся на катоде, формируется в виде пузырькового клина, толщина которого растет по длине радиуса МЭЗ [4]. Разделим межэлектродное про- странство условно на две области: 1 и 2 (рис. 2). В области 1 пузырьков мало и они небольших размеров. Поэтому эту область приблизительно можно считать жидкой фазой. Область 2 - газожидкостная, в ней количество пузырьков и их размеры быстро растут по мере удаления от центра МЭЗ.

Общая электроактивная площадь кольца 1 равна разности полной и токоизолированной площадей:

V = V ■ f.

1 эл . акт     ^Mi n J 1 ,

где

f = 1 -

A l ■ N

п ■ D

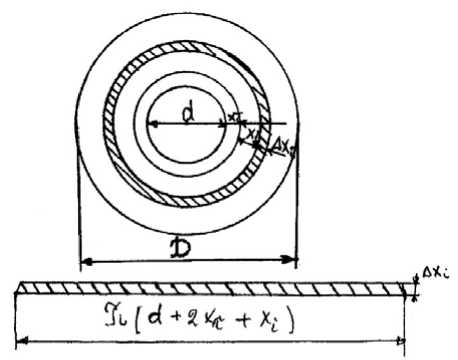
Рис. 2. Расчет области межэлектродного промежутка

- коэффициент уменьшения площади катода изоляторами в количестве N штук.

Количество тепла, выделенное электроактивной поверхностью катода, определится по формуле Джоуля-Ленца:

e r = 0,24 ( и -A и ) ■ i cp ■ A 1 n ■ f l ■ T ,

где и - напряжение на электродах; A и - сумма анодного и катодного потенциалов. Это тепло перешло в электролит, движущийся в МЭЗ:

Q Г = w ■ P r ■ c '^v' / 2 ‘^A t^{T ,}

где _w - объем кольца 1; p _r - плотность электролита; v -абсолютная скорость точки электролита; A t — T_T - T ₀ -разность температур на входе и выходе в область 1; f , -коэффициент расхода электролита, учитывающий ту часть электролита, которая участвует в переносе тепла.

Найдем объем кольца 1 по формуле

Длина участка 1 должна быть не более x_T — v T , здесь v - абсолютная скорость точек электролита: 4 .6с ^— Ч ,т„ ⁺ 4с _Р ( й _от „ - относительная скорость, ^v „ _ep -пе- _ „ _ (^d , ?

реносная скорость v„cp — I — + x I-to); так как движение _ „ пп равномерное, то to — -30 . Параметр т - время роста пу-

w — п ( d + x_T ) ■ x_T ■ h ,

где h - усредненное межэлектродное расстояние.

Определим f , . К расчету коэффициента f l добавим, что катод вращается равномерно с и оборотами в минуту, поэтому рабочий участок сместится на величину по окружности

зырька водорода до установившихся размеров [2],

T =     ^A w ■ ^р г    ,

П г ■ « Г ■ icp '^{A F}

A А =

Далее получим

^п ■ ^d ■ ^{n T} 60

где A w - объем пузырька водорода с установившимся размером; AF - площадь поверхности проекции пузырька на катоде; Р _Г - плотность газа; а _г -электрохимический эквивалент водорода; п _г - коэффициент выхода по току водорода; i_cp - средняя плотность тока на участке 1.

На катодной поверхности N секторов с дугой A l на внешней окружности покрыты токонепроводящим материалом. Поэтому в выделении тепла будет участвовать только часть площади кольца области 1. Из фигуры ЛОД

f _— W-T.

f2   w ,

n где Wn — п (d + xT) xT ■ h - полный объем кольца 1;

W _n . _T — п ( d + x _T ) x _T ■ h -

A l ■ ( d + x _T ) x _T • h ■ N + п ( d + x _T ) x _T • n ■ N ■T

D

та часть объема, которая участвует в переносе тепла. Аналогично формуле (3)

d , x_r ,,    ( d + x _r)-A I

(рис. 3) дуга A l x с радиусом — + -^ , A l x — 2---- ^T ---;

_ , A l ■ N N ■ n ■t f = 1-- +------.

² п ■ D 60

D

Так как Q r — Q 2 T , то подставляя (4) и (5), получим ^A t ■ ^w ■ P r ■ ^c ‘ ^v ■ / 2 ^T = 0,24 ( U ^-A U ) ■ i _cp ■ ^s 1 „ ■ f_x -^T , где

( d + x_T ) ‘A l ■ x_T ■ N

.

A ,„ = п ( d + x, ) ■ x, ; S, ^{1 n                   T T}      1 изол

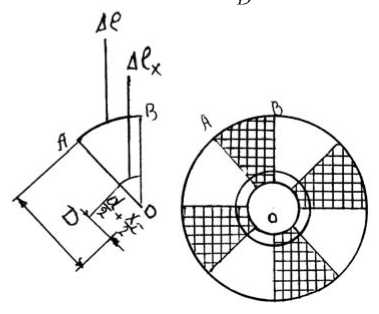
Рис. 3

_A t _— 0,24 ( и -A и ) ■ i cp ■ A i n ■ f l

^w ■ P r ■ ^c ‘^v ■ / 2 но A t — T_T - T ₀ , откуда

Tt — T o +

,

0,24 ( и -A и ) ■ i cp ■ A n ■ f

w ■ P r ■ ^c ‘^v ■ / 2

.

(Ю)

Этой формуле можно придать другой вид, учитывая, что i 1 cp = ( и -A и ) ■ х , где X = Х 0 ‘[1⁺ Р ( ^T 0 ^{- T} t ) ] , здесь X , ^х 0 - удельная электропроводность и удельная электропроводность электролита на входе, в - температурный коэффициент электропроводности, формула (9) примет вид

0,24 ( ^{и -A и} ) 2 х . 0,24 ( ^{и -A и} ) 2 X ■ Р ...

A t —-- 1--- A t .

w-p -c-p-L w p -c-p-L r        2           r        2

Введя вспомогательные обозначения, получим A t = a + b ■A t , откуда A t =---- , или

1- b

T = T + —. τ 0 1 _- b

Проведем аналогичный расчет температуры для газожидкостной области 2. Для этого разобьем область 2 на элементарные частички в виде концентрических колец (рис. 2). Здесь А А 2 n = п ( d + x_T + x J-A x i , A W 2 = п ( d + x_T + x i ) ■ h -элементарная площадь и элементарный объем выделенной произвольной частицы. Усредненное приращение температуры для выделенного элементарного объема

_{∆ t =} 0,24 ( u -∆ u ) ⋅ i cp ⋅∆ S 2 n ⋅ f 1

,

^A W i ■ Р г » ■ ^си■ / 1

где р_г . _ж = р_ж - ( 1 - ф ) + р_г ■ Ф - плотность газожидкостной смеси в межэлектродном зазоре; ф - коэффициент объемного содержания газовой фазы, равен отношению объема, занимаемого газом, ко всему выделенному

W объему, т. е. ф = -W. Отсюда аГ ■ ПГ ■ icp ■ f ϕ=

Р » ^U ■ h ep

.

Суммируя результаты (12) по всей площади кольца, получим d+x +x τ1

T =T+ x1      τ d+xτ

0,24⋅ ( u -∆ u ) ⋅ i x ⋅∆ S 2 n ⋅ f 1 ------- ------------------------dx .

A W ■ Р г» ■ с ■ и ■ f 2

Количество растворенной массы обрабатываемой детали в области 1, перешедшее в раствор, определится по закону Фарадея:

m l = ^а м«„ ■ П мет ■ i 1 ер ■ ^А 1 и ■ f 1 ^Т .

Формуле (15) можно придать другой вид, учтя, что 1 1 cp = ( u ^-A u ) ■ X :

m l = П „,„ ' « м™ ■ ( u ^-A u ) ' X 0 ( ^{1 + в} ^ ep ) ( d ⁺ x T ) ' x T ■ f 1 ■ ^T , (16) где а _мет - электрохимический эквивалент металла детали; П _мет - коэффициент выхода по току металла детали.

При вычислении растворенной массы детали в области 2 соответствующую область разбивают на элементарные частицы, масса которых определится по формуле А/щ=п а -7 -АУ -Д-Ах-Ат (17) 2 «мет мет хер 2 и 2 2              .          у-¹-

Суммируя элементарные массы всех колец, получим

d

+ x + x 2 ^τ

τ _x

T 2 x = T τ +0,24⋅ ∫   ∫

τ

Общая масса

d

₂ + x _τ

( u -∆ u ) ⋅ i x ⋅ f 1

---------------dTdx .

h ■ Р г» ■ c ■^и ■ f >

M = m + m 2 .

Сравнение результатов эксперимента с расчетными значениями, полученными по формулам (14) и (18), позволяет путем варьирования параметров направлять электрохимический процесс в сторону интенсификации ЭХО. Но эксперимент показывает, что очень часто отклонение параметров от их значений для установившегося электрохимического процесса приводит к тому, что движение электролита в МЭЗ переходит в пульсационный режим, при котором в определенный момент межэлектродный канал запирается. В экстренных случаях это приводит к короткому замыканию.

Авторами работы [5] получен критерий устойчивости электрохимического процесса в удобном для практического использования виде:

( u -∆ u ) ⋅ χ ⋅ α ⋅ R ⋅ T ⋅ L

------)^^^------< 1 ,        (19) υ ⋅ p ⋅ h ²

где и - скорость электролита в МЭЗ; L - длина канала;

Т- температура электролита.

В работе [6] получено выражение для определения

МЭЗ:

• 2    ( u -∆ u ) ⋅ χ ⋅ α_H ⋅ R ⋅ T ⋅ L

^h 0M„ =     J------------------------.        (20)

• 3            υ ⋅ p

При варьировании параметров электрохимического процесса желательно, наряду с уравнениями (14) и (18), учитывать и уравнения (19) и (20).

Общеизвестно [4], что при сравнительно низком уровне вводимой в МЭП мощности отсутствует эффект запирания, но дальнейшее увеличение подводимой мощности приводит к появлению этого эффекта. Чем выше уровень мощности, тем быстрее этот эффект наступает. Авторами работ [7; 8] показано, что величина произведения потока мощности, вводимой в МЭП, на время его запирания в пределах ошибки эксперимента является для данного сопротивления ячейки постоянной, т. е.

^W m. L • ^U • U = const ,           (21)

где I a - амплитудная плотность тока; U - напряжение; t_3m - длительность импульса до появления срыва тока, характеризующего запирание. Изменение сопротивления лишь перераспределяет составляющие энергии. Для конкретной технологической системы максимальная энергия запирания есть постоянная величина и если ее значение изменить, то оно определяется однозначно и наоборот, т. е. изменение одного параметра системы самой системы однозначно определяется как изменение другого параметра. Это позволяет считать, что процесс ЭХО металлов является саморегулирующимся по параметрам ввода энергии.

Зависимость потока мощности, вводимой в МЭП, от времени его запирания (рис. 4) разделяет область возможных параметров импульса для импульсной ЭХО металлов на две области. Область параметров, лежащих выше ее (область 2), является запрещенной для ЭХО, так как характризуется появлением в МЭП условий, предопределяющих развитие электрического пробоя.

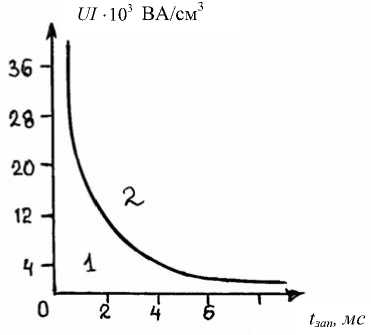
Рис. 4. Зависимость амплитудного потока мощности, вводимого в МЭП от времени запирания его для раствора хлористого натрия концентрацией 80 г/л

Исходя из вышесказанного и учитывая зависимость амплитудной плотности тока от времени запирания и вольт-амперных характеристик для разных электродных промежутков (рис. 5), необходимо отметить, что для интенсификации ЭХО процесс следует проводить в импульсном режиме при минимальной длительности импульса с максимальными значениями составляющих мощности (тока и напряжения).

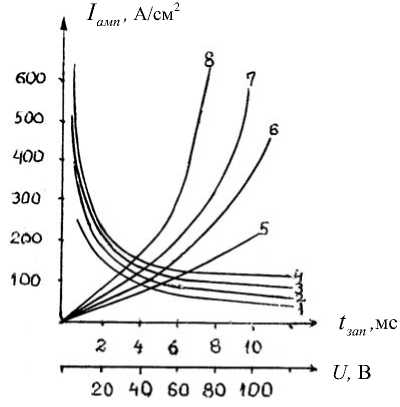
Рис. 5. Зависимость амплитудной плотности тока (1...4) от времени запирания промежутка и вольт-амперные характеристики (5...8), полученные в растворе хлористого натрия концентрацией 80 г/л при зазорах, мм: 0,8...1,5;

0,5...2,6;0,3...3,7;и0,2...4,8

В заключение сдлеаем следующие выводы:

• -    максимальная точность и качество поверхности при ЭХО деталей наблюдается в момент сближения электродов с прекращением подачи напряжения в момент их контактирования и последующего удаления оксидной пленки;

• -    существенное влияние на точность и качество поверхности деталей при ЭХО оказывает вибрация катода-инструмента при условии, когда она формирует МЭЗ;

• -    предложенная модель расчета параметров ЭХО при вибрации и вращении катода-инструмента позволяет

выбрать рациональные технологические параметры ЭХО;

• -    для интенсификации ЭХО процесс следует проводить в импульсном режиме при минимальной длительности импульса с максимальными значениями составляющих мощности (рабочего тока и напряжения).