Моделирование процесса мягкой посадки лунного взлётно-посадочного модуля с механическим посадочным устройством

Одной из важнейших научно-технических задач, содержащихся в Федеральной космической программе 2016–2025 гг., является доставка экипажей и грузов на Луну [1]. О перспективности этой задачи свидетельствуют проводимые как в нашей стране, так и за рубежом, исследования проблемы посадки на Луну [2–8] и состоявшиеся в последнее время запуски на Луну космических аппаратов (КА) такими странами как Индия, Китай, Россия, США, Япония. Неудача с посадкой российского космического аппарата на Луну в 2023 г. показала, что обеспечение успешной посадки является актуальнейшей научно-технической задачей и одним из наиболее критичных этапов функционирования КА.

Процесс посадки КА заканчивается его контактом с посадочной поверхностью и дальнейшим движением по ней вплоть до полной остановки. Большая часть кинетической энергии аппарата при спуске гасится либо тормозными аэродинамическими устройствами (парашютными системами, надувными ёмкостями и т. д.), либо (для планет с отсутствием атмосферы) тормозными двигателями [9–11]. Однако, вследствие погрешностей системы управ- ления спуском, в момент первого контакта с поверхностью КА обладает некоторой остаточной скоростью центра масс (до нескольких метров в секунду) и угловой скоростью (до 10-15 °/с). При существенной массе аппарата (которая может составлять десять и более тонн) его кинетическая энергия велика и должна быть погашена при движении по поверхности. С этой целью аппарат снабжается посадочным устройством, содержащим энергопоглощающие элементы, при обжатии которых и происходит рассеяние кинетической энергии [11–13].

Наиболее распространёнными являются механические посадочные устройства различных кинематических схем [11, 14–16]. Ниже рассмотрен процесс трансформации опор механического посадочного устройства перспективного лунного взлётно-посадочного модуля (ЛВПМ) на участке контакта с лунной поверхностью.

Постановка задачи

В процессе посадки должен выполняться ряд следующих требований:

• •    непревышение некоторых предельно допустимых значений перегрузки с целью сохранения здоровья экипажа и работоспособности приборов и систем;

• •    отсутствие опрокидывания при движении по поверхности;

• •    недопустимость контакта корпуса ЛВПМ с поверхностью (клиренс не должен быть меньше минимального допустимого значения).

Кроме того, итоговая ориентация ЛВПМ должна обеспечить возможность выхода экипажа или скатывания лунохода [11].

При наземной экспериментальной отработке посадки не удаётся в полной мере воспроизвести реальные условия [14, 17]. В связи с этим, основным способом подтверждения принимаемых технических решений, особенно на предварительных этапах разработки конструкции посадочного устройства, является моделирование с максимальным учётом существенных особенностей процесса посадки.

конструкция посадочной опоры

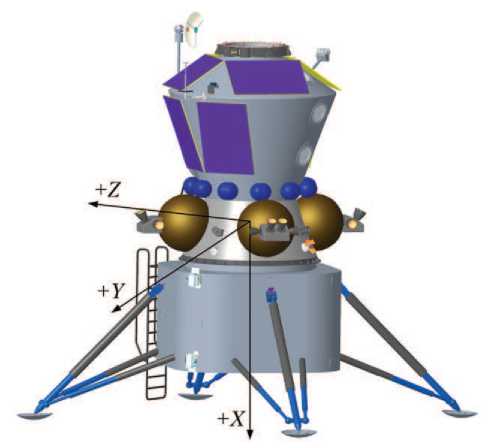
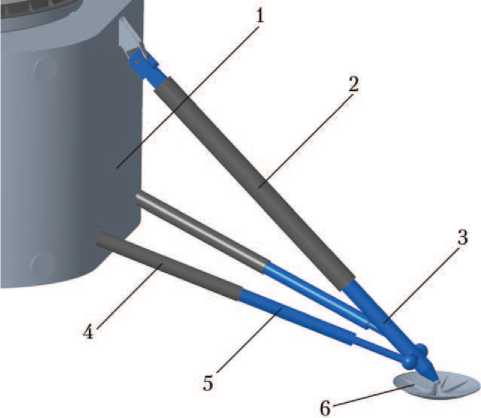
Механическое посадочное устройство ЛВПМ состоит из четырёх трансформируемых посадочных опор с их равномерным азимутальным расположением через 90 ° (рис. 1, а ). Конструкция посадочной опоры представлена на рис. 1, б .

а)

б)

Рис. 1. Общий вид (а) и схема посадочной опоры (б) лунного взлётно-посадочного модуля (ЛВПМ): XYZ — система координат, связанная с центром масс ЛВПМ; 1 — корпус; 2 — стакан основной стойки; 3 — шток основной стойки; 4 — стакан подкоса; 5 — шток подкоса; 6 — опорная тарель (рисунки созданы автором)

динамическая модель системы

Проблеме моделирования процесса мягкой посадки различных аппаратов посвящён целый ряд работ. К примеру, в работах [9, 18–21] рассматривался процесс посадки российского перспективного транспортного корабля нового поколения, в т. ч. в нештатных ситуациях [22–24]. В работах [10, 25] анализировался процесс посадки на поверхность Марса, в работах [16, 26–28] — на грунты Венеры и Фобоса. В работе [29], посвящённой научно-техническому обзору отечественной лунной программы, представлен целый ряд вариантов посадочного устройства (ПУ) лунного корабля и приведено обоснование выбранного варианта.

В работе [30] обсуждается принципиальный подход к созданию математической модели процесса посадки на лунную поверхность и программные средства, которые могут быть использованы при детальном анализе динамики посадки. Рассматриваемые в данной статье конструкция и кинематическая схема ПУ ЛВПМ оригинальны, отличаются от вышеупомянутых известных аналогов, в связи с чем задача разработки динамической модели, которая могла бы дать исчерпывающее представление о кинематике и динамике процесса посадки ЛВПК, представляется актуальной и полезной. Важно также подчеркнуть, что представленный ниже подход может быть адаптирован к возможным изменениям конструкции и кинематической схемы ПУ ЛВПМ.

Рассматривается следующая структура механической системы: корпус ЛВПМ; четыре опоры, каждая из которых содержит три амортизатора, один из них (основная стойка) крепится одним концом к корпусу, а другим — к тарели, непосредственно контактирующей с грунтом. Стойка состоит из стакана и штока, внутри стакана находится энергопоглотитель, чаще всего выполненный в виде сминаемых сот [11, 15, 21]. Кроме стойки опора содержит два подкоса, также состоящие из стакана и штока. Штоки подкосов соединены с корпусом и со штоком основной стойки (рис. 1).

Необходимо подчеркнуть, что величина хода обжатия амортизатора практически не является оптимизируемой величиной, поскольку лежит в очень узком диапазоне, жёстко задаваемом располагаемым компоновочным объёмом, схемой укладки и раскрытия посадочных опор. Рационально можно выбрать, в основном, профиль изменения силы

В ряде приложений динамики амортизатора в зависимости от располагаемого хода. Такого рода анализ, особенно если он проводится на начальных стадиях разработки ЛВПМ, может быть осуществлён только путём математического моделирования динамики процесса посадки, с проведением большого объёма расчётов.

Корпус ЛВПМ, стаканы, штоки, тарели рассматриваются как структурно сложная механическая система тел с внутренними связями, характер которых отвечает имеющимся степеням свободы в точках соединения отдельных тел. Конструктивно связь между корпусом, стаканами основной стойки и стаканами подкосов выполнена в виде шарнира Гука (кардана); связь между стаканами и штоками — в виде цилиндрических шарниров; между штоком основной стойки и тарелью — в виде сферического шарнира. Связь между штоком основной стойки и штоками обоих подкосов также выполнена в виде сферических шарниров (см. рис. 1).

структурно сложных систем к задачам ракетно-космической техники, таким, например, как процессы разделения ступеней ракет и частей космических аппаратов [31, 32], трансформации раскрываемых крупногабаритных конструкций [33, 34], эффективным оказался подход, в рамках которого каждое тело системы рассматривается как условно свободное, а действие на него других тел учитывается в виде сил и моментов реакций связей. Такой подход использован и для создания математической модели посадки ЛВПМ.

Для описания движения вводятся правые системы координат: инерциальная и связанные с центрами масс тел системы (рис. 2).

Для каждого i -го тела — корпуса ЛВПМ, стакана, штока и таре-ли (далее в формулах обозначены индексами «кор», «ст», «шт» и «тар» соответственно) — записываются уравнения движения центров масс

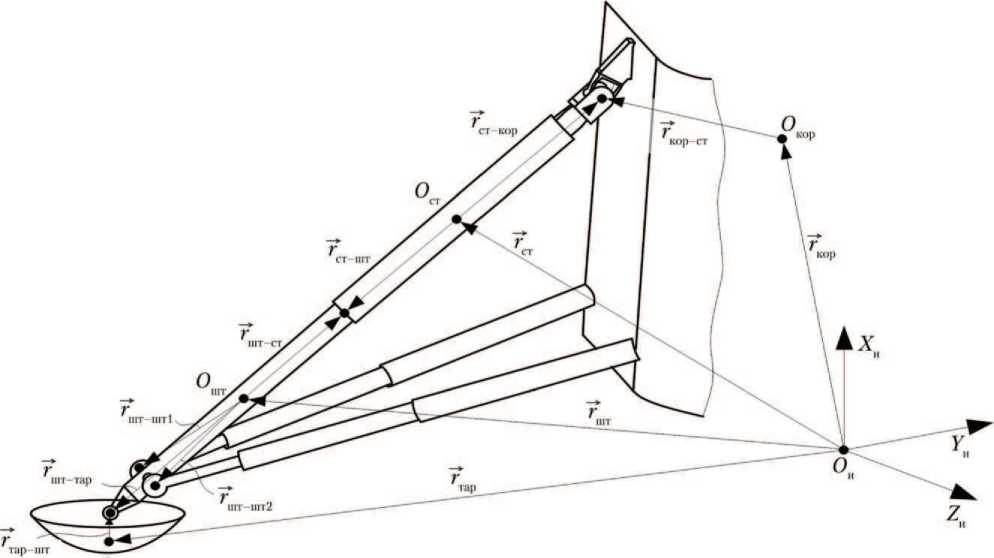
Рис. 2. Расчётная схема опоры посадочного устройства: O _и X _и Y _и Z _и — инерциальная система координат; O _кор , О _ст , О _шт , О _тар — центры связанных систем координат корпуса лунного взлётно-посадочного модуля (ЛВПМ), стакана основной стойки, штока основной стойки и тарели соответственно; "Тор , 7 т , 7 , Т ар — радиус-векторы, определяющие положение центров масс корпуса ЛВПМ, стакана основной стойки, штока основной стойки и тарели соответственно в инерциальной системе координат; Т ор^т , 7_р_о_р — радиус-векторы, определяющие положение точки контакта корпуса и стакана основной стойки в связанных системах координат каждого из тел; 7т_ _ш,, Т^ т — радиус-векторы, определяющие положение точки контакта стакана и штока основной стойки в связанных системах координат каждого из тел; Т^ шт^ ; 7 ш _т-шт2 — радиус-векторы, определяющие положение точек контакта штока основной стойки и штоков подкосов в связанных системах координат каждого из тел; 7_{ш -}_ а _рр ; Т аршт — радиус-векторы, определяющие положение точки контакта штока основной стойки и тарели в связанных системах координат каждого из тел (рисунок создан автором)

(в инерциальной системе координат) и вращения относительно центров масс (в связанных системах координат тел):

m_i a _i = F_i ;                                      (1)

[ J ] ] a i + Ю i X ([ J ] ] Ю ) ) = 4,                  (2)

где i — номер тела; m_i — масса i -го тела; a _i — вектор ускорения центра масс i -го тела; F_i — главный вектор сил, действующих на i -е тело, включая силы реакции связей; [ J_i ] — тен з ор инерции i -го тела; e i — вектор углового ускорения i -го тела; ю i — вектор угловой скорости i -го тела; L_Oi — главный вектор моментов относительно центра масс i -го тела, включая моменты от сил реакции связей.

уравнения связей

Корпус и любой из стаканов соединены связью в виде шарнира Гука (кардана), запрещающего в точке связи линейные относительные перемещения и вращение относительно общей продольной оси. В соответствии с предлагаемым подходом, движение каждого тела рассматривается отдельно. Тогда действие стакана на корпус ЛВПМ учитывается в виде силы реакции (трёх её неизвестных проекций на какие-либо координатные оси) и одной проекции момента связи на общую продольную ось (рис. 3, 4).

На стакан со стороны корпуса ЛВПМ действует сила, равная по модулю и противоположная по направлению, а также момент связи противоположного направления. Первое уравнение для определения этой силы реакции связи основано на условии нерасхождения точки контакта корпуса ЛВПМ и стакана:

r кор ⁺ r кор–ст ⁼ r ст ⁺ r ст–кор^,

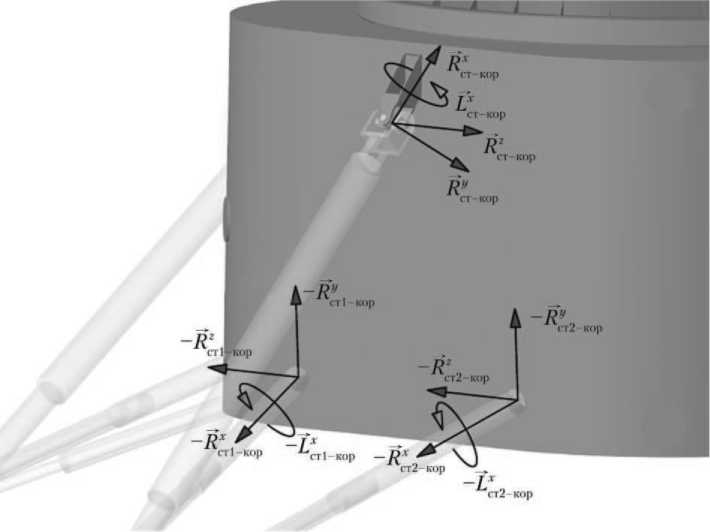
Рис. 3. Силы R и моменты L взаимодействия корпуса (индекс «кор») со стаканами (индекс «ст») стойки и подкосов по осям X, Y, Z (рисунок создан автором)

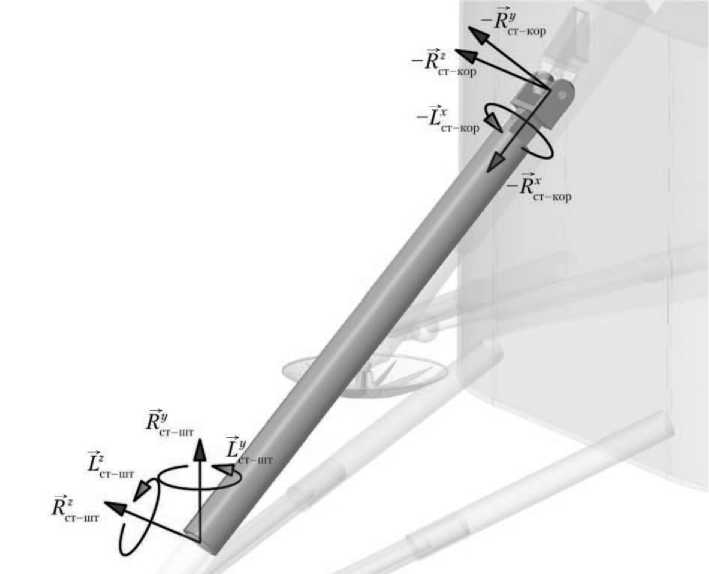
Рис. 4. Силы R и моменты L взаимодействия стакана (индекс «ст») стойки с корпусом (индекс «кор») и штоком (индекс «шт») (рисунок создан автором)

где rкор, rст — радиус-векторы, определяющие положение центров масс корпуса ЛВПМ и стакана в инерциальной системе координат соответственно; rкор–ст, rст–кор — радиус-векторы, определяющие положение точки контакта в связанных системах координат каждого из тел (см. рис. 2). Смысл двойной индексации векторов rкор–ст, rст–кор следующий: первый индекс означает принадлежность к данному телу, второй — индекс тела, с которым данное тело взаимодействует.

При двойном дифференцировании получаем a кор

+

^£ кор ^{X Г} кор-ст

+

^ю кор ^{х ( ю} кор ^{х г} кор-ст ) = a ct ⁺

£ ст

X г ст–кор

+ (О X (ю X г

ст–кор .

Из уравнений (1)

и (2) можно

и

выразить

ускорения

центра

масс

и

угловые стакана:

ускорения

корпуса

a = m ^–1 кор кор

кор ^ ^ст-кор у; k, j

a ст

= m ^–1 F – R

cт

ст

ст–кор ст–шт ;

кор ^{[ J} кор^]

-О кор

^X Ц J кор ] ^Ю кор

+ М кор

F кор

+

^{Е Г} кор-ст ^X R k, j

ст–кор

+

Е L

ст– k, j

кор

;

^£ ст = [ J ст ]^{-1   - ю} ст ^X   J ст ]      ⁺ М ст F^F ст) ^{+ г} ст-кор ^{X -} R ст-кор) ^{- L} ст-кор ^{+ г} ст-шт ^X R ст-шт ^{+ L} ст-шт Г ⁽⁷⁾

В выражениях (4)–(7) F _кор , F _ст — главные векторы внешних сил, действующих на корпус и стакан; R _{ст–кор} , R _ст–шт — главные векторы сил реакций связей, действующих в точках связи между стаканом и корпусом и между стаканом и штоком; М _кор ( F _кор ), М _ст ( F _ст ) — главные моменты внешних сил, действующих на корпус и стакан; L _{ст–кор} , L _ст–шт — главные реактивные моменты, действующие в точках связи между стаканом и корпусом и между стаканом и штоком; в знаках суммирования индексом k обозначено количество опор (для данной схемы k = 1, 2, 3, 4), а индексом j — количество стаканов в опоре ( j = 1, 2, 3).

Подстановка выражений (4)–(7) в равенство (3) даёт первое искомое уравнение связи между корпусом ЛВПМ и стаканом, окончательный вид которого не приводится из-за громоздкости.

Второе уравнение связи между корпусом ЛВПМ и стаканом отражает равенство проекций их угловых скоростей на общую продольную ось х (см. рис. 2, 3):

ю к _ор - ® _ст = 0-

Дифференцирование последнего равенства даёт:

• ^£кор ^{- £}ст ^{+ Ю} кор ^{X Ю} ст = 0-                    ⁽⁸⁾

Второе уравнение для определения реакций связи получается подстановкой выражений (4)–(7) в соотношение (8).

Связь между стаканами и штоками выполнена в виде цилиндрических шарниров. Поскольку связь позволяет относительное движение стакана и штока вдоль общей продольной оси и относительный проворот относительно этой оси, то сила реакции связи имеет две компоненты, перпендикулярные продольной оси. Также имеются две компоненты момента, направленные таким же образом (рис. 5). Для определения сил и моментов реакции необходимо также записать уравнения связи. Первое из уравнений связи основано на равенстве радиус-векторов точки контакта стакана и штока в инерциальной системе координат (см. рис. 2):

• r ст ⁺ r ст–шт ⁼ r шт ⁺ r шт–ст^.

При двойном дифференцировании этого равенства получаем:

a ct + ACT ^X A ст-шт + ® ст ^X ''' ^X A Ст-шт) + ² ® ст ^X

~~ dr      d2r ст–шт + ст–шт dt      dt2

= ^А шт + ⁸ шт ^{X r} ст-шт + ^Ю шт ^X

^Ю шт ^{X r} шт-ст

,

~~ dr        d2r ст–шт        ст–шт где dt ,     dt2

локальная отно-

Локальная скорость

~ dr ст–шт

dt

опреде-

сительная ускорение

скорость и относительное

ляется следующим образом:

~

dr

ст–шт

движения штока внутри стакана соответственно.

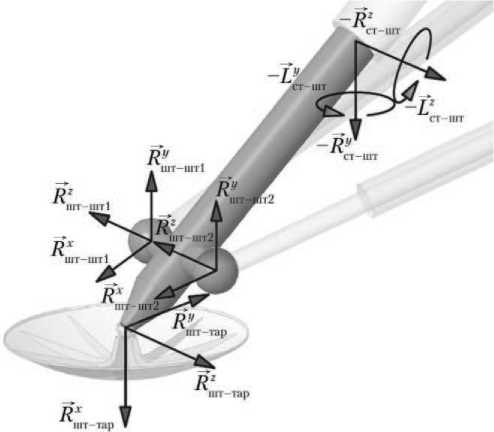
Рис. 5. Силы R и моменты L взаимодействия штоков (индекс «шт»), стаканов стойки и подкосов (индекс «ст») и тарели (индекс «тар») по осям X, Y, Z (рисунок создан автором)

шт

= [ J шт ]^-1) ^{- ю} шт ^X

( [ J шт ] ^ю шт

+

шт–тар шт–тар ст–шт

dt

- ю

ст

= V – V

шт cт

+ ю

шт

X г -

шт–ст

^{X г} шт ^{- г} ст ^{+ г} шт-ст

где V _шт , V _cт — скорости центров масс штока и стакана в инерциальной системе координат соответственно, а радиус-вектор переменного модуля

r ст–шт ⁼ r шт ^– r ст ⁺ r шт–ст^.

Ускорение центра масс стакана a _ст определяется выражением (5), угловое ускорение е _ст — выражением (7).

Для штока аналогичные параметры определяются следующим образом:

А = т-1 (F - R + R + E R a (11)

шт шт шт ст-шт шт-тар j = 12 шт-шт j

М шт

F шт

+ r

шт–ст

X

ст–шт

+ E A X R j = 1 2 ^шт-шт j

шт–шт j

,

где j = 1, 2 — количество штоков подкосов, соединённых со штоком основной стойки. Уравнение для определения реакций связи получается подстановкой выражений (5), (7), (10)–(12) в равенство (9).

Второе уравнение связи между стаканом и штоком основано на равенстве проекций их угловых скоростей на оси y , z , ортогональные продольной:

ю_ - ю шт = 0.

дифференцирования последнего получаем следующее выражение:

ст

После равенства

е

ст

е шт ⁺ ю _ст x ю шт = 0.

Уравнения для определения реакций связи получается подстановкой выражений (7) и (12) в соотношение (13).

Связь между штоком и тарелью выполнена в виде сферического шарнира. Тот же тип связи — сферический шарнир — между штоком основной стойки и штоками подкосов. Поскольку сферический шарнир допускает лишь пространственное вращение соединённых им тел, в точке связи неизвестными будут только три компоненты силы реакции связи (рис. 5). Уравнение для этого типа связи будет иметь вид, аналогичный полученному выше выражению (3), с соответствующей заменой индексации радиус-векторов. Однако, в отличие от соотношений (3) и (9), они будут проецироваться на все три оси координат.

Полученная система уравнений связи линейна относительно неизвестных компонент реакций связей Rст–кор, Lст–кор, Rст–шт, Rшт–тар, Rшт–штj, Lст–шт. Коэффициенты при неизвестных этой системы переменны по времени, так как зависят в т. ч. и от кинематических параметров тел в каждый конкретный момент времени (угловых и линейных скоростей тел, радиус-векторов характерных точек и др.).

Пример реализации

Рассмотрен процесс выбора энергетических характеристик амортизатора для случая штатной посадки ЛВПМ на абсолютно ровную поверхность без локальных бугров и впадин как естественного, так и искусственного происхождения (за счёт газодинамического воздействия струй двигательной установки на грунт в процессе посадки). Предполагалось, что приемлемость любого варианта расчёта обеспечивается при непревышении продольной перегрузкой некоторого предельного значения, в данном случае равного восьми единицам, а также обеспечением в течение всего процесса движения аппарата по посадочной поверхности определённого минимального клиренса, значение которого принято 0,4 м. Обязательным требованием также является устойчивость движения (отсутствие опрокидывания или кувырков).

Грунт интерпретировался реологической моделью Фойгта [35,  36], для тарели сферической формы диаметром dт = 0,8 м. В расчёте принимались параметры, соответствующие скальным земным грунтам с жёсткостью Сг = 7 ∙ 107 кгс/м3 и вязкостью Пг = 1 • 105 кгс-с/м3.

К моменту касания грунта, в случае штатной посадки, система управления аппарата обеспечит следующие параметры движения, являющиеся начальными условиями для расчёта посадки:

• •    вертикальная скорость снижения V _в = (0 ± 0,5) м/с;

• •    горизонтальная скорость V _г = (0 ± 0,5) м/с;

• •   угловая скорость   относительно

любой из осей аппарата го = (0 ± 5) ° /с;

• •    угловое отклонение продольной оси аппарата от вертикали 0 = (0 ± 5) ° .

Для нештатных случаев посадки возможно превышение указанных выше скоростей и углов подхода. Кроме того, возможен учёт силы тяги последействия тормозного двигателя (в случае необходимости его использования).

Целью практического анализа является подбор таких энергетических характеристик амортизаторов, при которых выполняются не только указанные выше ограничения по продольной перегрузке, клиренсу и устойчивости, но и конструкционные ограничения по располагаемому ходу амортизаторов.

Проведённые расчёты показали, что при соответствующем выборе профиля энергетической характеристики амортизатора (рис. 6) вышеприведённые ограничения могут быть выполнены. Характеристика представляет собой зависимость усилия F _ам от хода штока h _ам амортизатора, имеет линейный участок начального обжатия и две ступени порогового усилия 6,5 и 8,0 тс. Кроме того, до момента касания с посадочной поверхностью амортизатор имеет некоторое начальное усилие, которое часто называют начальным обжатием (на графике значение F _ам при h _ам = 0 м). Градиент выхода на первое пороговое усилие и величина этого усилия (6,5 тс) подобраны таким образом, чтобы в случае штатной посадки выполнялось ключевое ограничение по значению максимально допустимой вертикальной перегрузки.

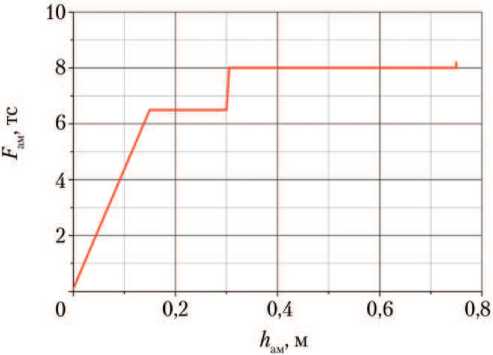
Рис. 6. Силовая характеристика амортизатора опоры лунного взлётно-посадочного модуля: F_ам и h_ам — усилие и ход амортизатора соответственно (рисунок создан автором)

Для нештатных случаев, где имеются более высокие скорости и большие углы подхода к поверхности, после отработки первой ступени амортизатор переходит на вторую (8,0 тс), но только в том случае, если нагрузка на шток амортизатора превысит первое пороговое усилие. Таким образом, наличие второй ступени позволяет погасить более высокую кинетическую энергию, характерную для нештатных случаев посадки. Важно отметить, что данная энергетическая характеристика амортизатора актуальна для конкретной конфигурации космического аппарата и геометрии ПУ.

Перегрузка (рис. 7) при рассматриваемых начальных параметрах не превышает допустимых границ. В момент первого контакта с посадочной поверхностью перегрузка имеет максимальное значение — первый выброс, затем происходят затухающие колебания — как следствие работы ПУ. Данные приведены в системе координат, связанной с центром масс ЛВПМ (см. рис. 1, а ).

На рис. 8 показан клиренс для корпуса ЛВПМ. Соударение днища ЛВПМ с поверхностью не происходит.

На рис. 9 и 10 показаны проекции центра масс и угловой скорости ЛВПМ на оси x , y , z .

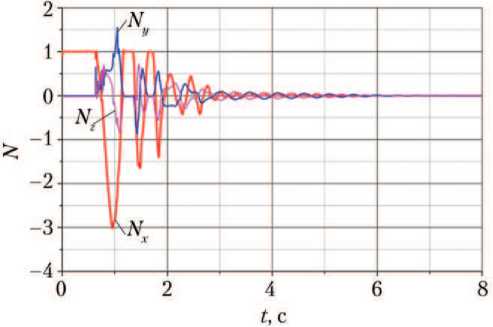
Рис. 7. Перегрузка лунного взлётно-посадочного модуля N, действующая на корпус относительно осей x, y, z соответственно (рисунок создан автором)

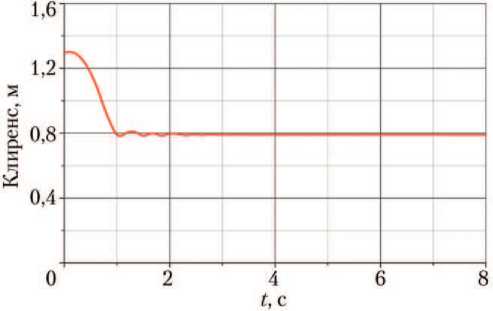
Рис. 8. Клиренс лунного (рисунок создан автором)

взлётно-посадочного модуля

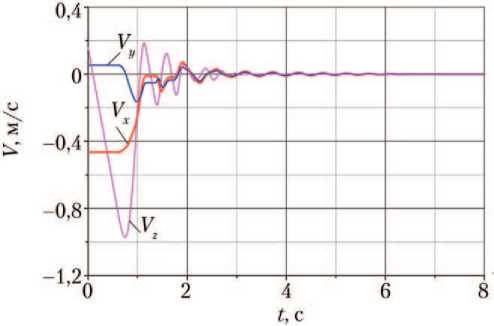
Рис. 9. Скорость центра масс лунного взлётно-посадочного модуля V относительно осей x, y, z соответственно (рисунок создан автором)

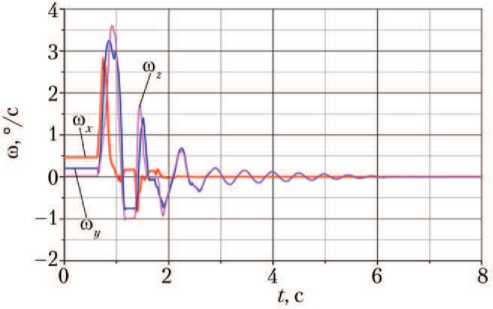
Рис. 10. Угловая скорость лунного взлётно-посадочного модуля ω относительно осей x, y, z (рисунок создан автором)

выводы

Разработана математическая модель процесса посадки ЛВПМ, базирующаяся на представлении лунного взлётно-посадочного комплекса как структурно-сложной механической системы, включающей в себя корпус модуля и элементы опор его посадочного устройства. Записана специальная система уравнений связей для определения реакций взаимодействия опор посадочного устройства с корпусом модуля, а также взаимодействия отдельных элементов посадочного устройства между собой. Для определения силы взаимодействия тарелей опор посадочного устройства с лунной поверхностью используется реологическая модель Фойгта.

Модель позволяет детально анализировать кинематику и динамику процесса посадки на участке контакта с лунным грунтом при штатных условиях посадки и может быть адаптирована к возможным отказам элементов посадочного устройства.

На базе модели осуществлён выбор характеристик посадочного устройства, при котором выполняются специфические требования к процессу посадки по максимально допустимой перегрузке, устойчивости и достаточности рабочего хода обжатия энергопоглотителей.

Рассмотрен случай штатной посадки ЛВПМ. Определены зависимости от времени перегрузок, действующих на корпус, скоростей центра масс корпуса и угловых скоростей, клиренса, на основании которых сделан вывод об успешности процесса штатной посадки.