Моделирование процесса отражения зондирующего радиосигнала от поверхности жидкости и стенок резервуара

В настоящее время в промышленных системах управления технологическими процессами широкое применение находят измерители уровня заполнения технологических резервуаров, выполненные на базе частотно-модулированных радиодальномеров. Для получения высокой точности измерения с помощью таких уровнемеров необходимо учитывать не только сигналы, отраженные от зондируемой поверхности жидкости, но и многочисленные сигналы, вызванные отражениями от стенок резервуара. Поэтому актуальной задачей является изучение особенностей отражения зондирующего радиосигнала от стенок вертикального стального резервуара и поверхности содержащейся в нем жидкости. 1

• 1.    Постановка задачи

Будем полагать, что внутреннее пространство резервуара облучается плоской однородной монохроматической волной. В большинстве практических приложений размеры резервуара много больше длины волны, поэтому отражение падающей волны происходит по законам геометрической оптики. В связи с этим при разработке математи- ческой модели используются следующие физические допущения:

• -    длина волны электромагнитного поля мала по сравнению с размерами резервуара;

• -    поверхность находящейся в резервуаре жидкости и внутренние стенки резервуара являются идеально гладкими;

• -    отражение электромагнитной волны от поверхности жидкости и стенок резервуара являются зеркальными.2

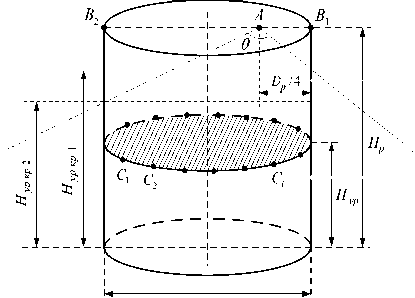
При моделировании процесса отражения зондирующего радиосигнала от поверхности жидкости и стенок резервуара в качестве основных информативных параметров будут выступать мощность и задержка отраженного радиосигнала. Эти параметры будем определять для трех характерных случаев (рис. 1):

• -    отражение зондирующего радиосигнала от поверхности жидкости;

• -    отражение зондирующего радиосигнала от верхних участков вертикальной стенки резервуара (точки B ₁ и B ₂ ), лежащих в плоскости, перпендикулярной плоскости размещения антенного устройства (точка A );

• -    отражение зондирующего радиосигнала от участков соприкосновения жидкости со стенками резервуара (точки C ₁, C ₂,..., C_n ).

  

  D /4

  C

  D р

  Рис. 1. Характерные точки резервуара для расчета характеристик принимаемого радиосигнала

  
  

• 2.    Характеристики принимаемого радиосигнала, обусловленного отражением зондирующего радиосигнала от поверхности жидкости

Задача состоит в нахождении совокупности математических выражений, позволяющих определить характеристики радиосигнала, отраженного от жидкости в резервуаре и его стенок.

В соответствии с основным уравнением радиолокации мощность принятого радиосигнала определяется соотношением [1]

• р _ P i3n G a ^— ^ эфф                           z, х

р       64 л ³ R ⁴    ’                        ()

где P _изл – мощность зондирующего сигнала; G _a – коэффициент направленного действия антенны; - - рабочая длина волны; о _э фф - эффективная площадь рассеяния цели; R – расстояние до цели.

Участок поверхности жидкости, облучаемый зондирующим радиосигналом, можно рассматривать как плоскую круглую пластину. Эффективная площадь рассеяния такой пластины определяется выражением [2]

• _ 4л-S Vеr -1

• ^{п эфф _}        /=77 ,

• - -Vеr +1)

где S - площадь пластины; еr - относительная диэлектрическая проницаемость жидкости.

При расчете эффективной площади рассеяния круглой пластины необходимо рассмотреть два случая:

• 1)    площадь участка отражения меньше площади поверхности жидкости;

• 2)    площадь участка отражения больше площади поверхности жидкости.

В первом случае площадь круглой пластины будет определяться расстоянием R от антенного устройства до поверхности жидкости и шириной диаграммы направленности антенны 0 :

S _ л R ⁴ tg ⁴ 0 .

Тогда эффективная площадь рассеяния круглой пластины будет равна:

_ 4л3 R4 tg4 0 f Ter -1Т

"_   -2   [:р>1 ,

Подставив полученное выражение (2) в формулу (1), получим выражение для принятой мощ- ности:

P _пр

Р изл G 2 tg ⁴ 0 Г ^ ^{- 1} У

• 16     I Ver +1,

  
  

Выражение (3) будет справедливо при выпол- нении условия Hур > Hур.кр 1, где Hур - высота уровня жидкости в резервуаре, H ур.кр 1 – высота уровня жидкости, при котором участок отражения не накрывает вертикальную стенку резервуара.

Величина H ур.кр 1 определяется следующим образом:

^H ур.кр1

Dр

4tg ^ГI

.

Во втором случае площадь круглой пластины будет зависеть только от диаметра резервуара:

л D 2 S _ —p

.

Эффективная площадь рассеяния будет равна: л ² d p f ve r ^r ) ²

^{Ст эфф _} - ² [ ve r ^r, '

Мощность сигнала на входе антенного устройства будет определяться выражением:

Р _    ^Р изл G a D 2   Г Vl r ^T) .         (4)

^р 64 л ( H p - H ур ) ⁴ ( ve r ^i J

Выражение (4) справедливо при условии

Hур < Hур.кр 2, где Hур.кр 2 - высота уровня жидко- сти, при котором участок отражения покрывает всю поверхность жидкости.

Формула для расчета H ур.кр 2 имеет следую- щий вид:

Н ур.кр 2

3 D р

.

⁴tg ( 2 )

Время задержки от момента излучения зондирующего радиосигнала до появления отраженного радиосигнала на входе антенного устройства определяется соотношением:

Моделирование процесса отражения зондирующего радиосигнала от поверхности жидкости и стенок резервуара

_ 2( ^H p - ^H ур )

^ з                      ,

c где c – скорость распространения электромагнитных волн.

Значения времени задержки радиосигнала, обусловленные отражением зондирующего радиосигнала от участков B ₁ и B ₂ , определяются выражениями:

3. Характеристики принимаемого радиосигнала, обусловленного отражением зондирующего радиосигнала от верхних участков вертикальной стенки резервуара

Участок вертикальной стенки резервуара, облучаемый зондирующим радиосигналом, можно рассматривать как плоскую прямоугольную металлическую пластину. Электромагнитная волна падает на эту пластину под прямым углом, поэтому для расчета эффективной площади рассеяния плоской прямоугольной пластины будем пользоваться выражением, предложенным в работе [2]:

Dр тч -    ; тч

З ¹     2 с ³2

3 D р 2 c .

° эфф -

2 ab ² X

cos2

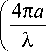
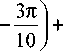
л³     . ₂ Г 4 л а 3 л)

+--------- 7 sin ²| —I ,

_Г 2 л а )     V ^{Х 10} V

2V Т)           _ где a, b– линейные размеры прямоугольной пла-

4. Характеристики принимаемого радиосигнала, обусловленного отражением зондирующего радиосигнала от участков соприкосновения жидкости со стенками резервуара

Участки соприкосновения жидкости со стенками резервуара C ₁, C ₂,..., C_n можно рассматривать как двугранные уголковые отражатели с прямым углом между гранями. Эффективная площадь рассеяния такого уголкового отражателя в вертикальной плоскости определяется как эффективная площадь рассеяния эквивалентной плоской пластины с линейными размерами a,b , которая располагается перпендикулярно падающему лучу.

Расчетное соотношение для эффективной площади рассеяния двугранного уголкового отражателя имеет следующий вид [2]:

стины.

Линейные размеры отражающей прямоугольной пластины можно определить, используя соотношение для границы дальней зоны [3]:

R > v, (6)

X где R – расстояние от фазового центра излучающей апертуры до точки наблюдения; L – линейный размер излучающей апертуры; λ – рабочая длина волны.

Используя соотношение (6), определим линейные размеры отражающей прямоугольной пластины:

a=b=L= Rλ , (7) где R – расстояние от антенного устройства до отражающего участка вертикальной стенки резервуара.

Отраженную мощность будем рассчитывать для двух участков вертикальной стенки резервуара B ₁ и B ₂ (рис. 1). Расстояния от антенного устройства до участков B ₁ и B ₂ определяются соотноше-

8 πa 2 b 2 ^σ эфф ⁼    _{λ 2}

sin

1 +

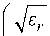
^2

V \°r ^ry

ниями:

Ri -

D р       3 D р

Т ^- R ^{2 -} —

где D _p – диаметр резервуара.

Подставив выражения (5) и (7) в формулу (1), получим:

2,5

Р изл G a I -I Р -______ ^{V R V пр}        32 л³

лХ . 2

+—Sin

8 R

2 cos2

+

, R ^- R i , ^R 2 .

2 π

— b sin y

где a, b – линейные размеры плоской прямоугольной эквивалентной пластины; ε_r – относительная диэлектрическая проницаемость жидкости; y - угол между падающим лучом и биссектрисой прямого угла двугранного уголкового отражателя.

Линейные размеры плоской эквивалентной пластины можно определить, используя соотношение (6) для границы дальней зоны:

a=b = R_iλ , (9) где R_i – расстояние от антенного устройства до i -го уголкового отражателя.

Расстояние R_i можно определить, используя приведенные на рис. 2 геометрические построения:

R i -

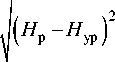
Г D p        D p Y D p² . 2

⁺1 ^cos ^ i "^1 ⁺ ^sin ^ i ,

0 < V i <  2 л .

Тогда угол между падающим лучом и биссектрисой прямого угла i -го двугранного уголкового отражателя будет равен:

^У- 4

arcsin

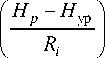
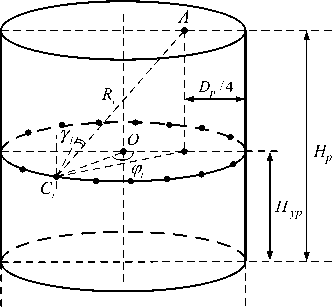
Рис. 2. К определению эффективной площади рассеяния уголкового отражателя

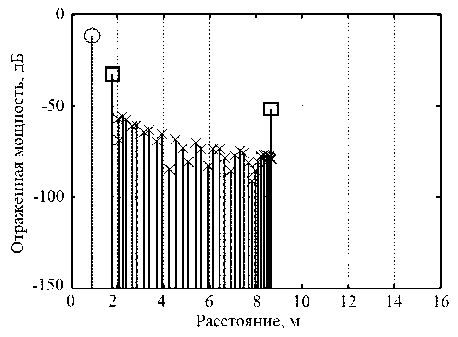
Рис. 3. Рефлектограмма внутреннего пространства резервуара РВС-1000: – отражение от поверхности жидкости;

– отражения от верхних участков вертикальной стенки резервуара; – отражения от участков соприкосновения жидкости со стенками резервуара

Подставив выражения (8)–(10) в формулу (1), получаем:

p _ ^ризл G a ^X \

P ^np "  8 R ² л 2 ^X

R   л sin 2л J — sin — arcsin

V X    4

R~ .Г л .

2 л J — sin — arcsin

V X I 4

p ур

I    Ri    ,

H p ~ H ур )

Ri    J)

1 +

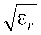
X

.

Выражение (11) будет справедливо при выполнении условия H ур <  H ур.кр 2 .

Значения времени задержки радиосигнала, обусловленные отражением зондирующего радиосигнала от участков соприкосновения жидкости со стенками резервуара C ₁ ,C ₂ , ... ,C_n , определяются

выражением:

Тз зi

2 c

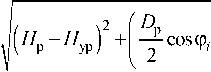
D р

^^^^ ^^^^^^^^^^M

²   D p ²

I + _T ^sin V i ,

0 < vi < 2л.

5. Представление характеристик принимаемых радиосигналов, обусловленных отражениями зондирующего радиосигнала от поверхности жидкости и стенок резервуара

Исследование процесса отражения зондирующего радиосигнала от поверхности жидкости и стенок резервуара удобно проводить с помощью рефлектограмм, которые представляет собой графические зависимости мощности отраженных сигналов от расстояния.

Рефлектограмма внутреннего пространства резервуара получается сложением мощностей сигналов, отраженных от поверхности жидкости, от участков вертикальной стенки резервуара B ₁ и B ₂ , а также от участков соприкосновения жидкости со стенками резервуара С ₁ ,C ₂ , ... ,C_n . На рис. 3 приведен пример рефлектограммы внутреннего пространства промышленного резервуара РВС-1000, рассчитанной с использованием разработанной выше математической модели процесса отражения зондирующего радиосигнала от поверхности жидкости и стенок резервуара.

Рефлектограммы внутреннего пространства резервуара позволяют оперативно и наглядно производить оценку уровня полезной мощности, отраженной от поверхности жидкости в резервуаре, а также уровня мощности радиосигналов, отраженных от стенок резервуара.

Заключение

Разработанная математическая модель процесса отражения зондирующего радиосигнала от поверхности жидкости и стенок резервуара позволяет решать задачи определения влияния различных факторов (размеров резервуара, длины волны зондирующего радиосигнала, уровня содержащейся в резервуаре жидкости, относительной диэлектрической проницаемости жидкости) на величину мощности отраженного радиосигнала, наблюдаемого на входе антенного устройства.