Моделирование процесса переноса теплоты через участки околошовной зоны одежды специального назначения в условиях нестационарной теплопроводности

СПЕЦИАЛЬНАЯ ЗАЩИТНАЯ ОДЕЖДА ПОЖАРНЫХ, ПЕРФОРИРОВАННЫЙ МАТЕРИАЛ, ПЕРЕНОС ТЕПЛОТЫ, МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ

Объектами исследования являются узлы и соединения специальной защитной одежды пожарных, изготавливаемой из огнетермостойких многослойных материалов с металлизированным покрытием.

Целью работы является математическое моделирование процесса переноса теплоты через неповреждённые участки околошовной зоны одежды специального назначения в условиях нестационарной теплопроводности на базе применения метода сеток.

Рассмотрена и формализована задача моделирования механизма переноса теплоты через участки околошовной зоны одежды специального назначения. Представлены математические зависимости, отражающие изменение температуры и плотности теплового потока на внутренней поверхности неповреждённых околошовных участков защитной одежды в условиях нестационарной теплопроводности. Получена обобщённая математическая зависимость в виде системы уравнений, позволяющая моделировать, последовательно воспроизводить процесс нагрева и определять температуру и плотность теплового потока на внутренней поверхности огнетермостойкого металлизированного материала в любой момент времени. Данная зависимость является базовой для дальнейшего исследова-

SPECIAL PROTECTIVE CLOTHING FOR FIREGUARD, PERFORATED MATERIAL, WARMTH TRANSFER, FINITE DIFFERENCE METHOD

The problem of modeling of the mechanism of a warmth transfer through sites which are located around a seam in clothes of a special purpose are considered and formalized. The mathematical dependence, reflecting temperature and heat flux density changes in an internal surface of the integrity of the sites which are located round a seam in protective clothes in the conditions of non-stationary heat conductivity is presented. The generalized model is received which allows to simulate, and consistently reproduce process of heating and to determine temperature and a heat flux density on an internal surface of the multilayered metallized material at any moment of time. Adequacy to the received mathematical model is confirmed experimentally.

ния и визуализации процесса переноса теплоты через перфорированные иглой швейной машины участки специальной защитной одежды пожарных от повышенных тепловых воздействий тяжелого типа в условиях нестационарной теплопроводности. Адекватность полученной базовой математической зависимости в виде системы уравнений подтверждена экспериментальными исследованиями.

Для обеспечения безопасных условий труда пожарных используется специальная одежда, защищающая от воздействия интенсивных тепловых потоков, высоких температур, механических и климатических воздействий. При её изготовлении в настоящее время все чаще применяются многослойные огнетермостойкие материалы. Металлизированные огнетермостойкие материалы на тканой основе обладают рядом преимуществ. Не теряя свойств, присущих текстилю (невысокая жёсткость, хорошая драпиру-емость, высокие прочностные характеристики), они приобретают свойства, присущие металлам (обладают электрической проводимостью, отражают тепловое и электромагнитное излучение).

При соединении деталей специальной защитной одежды из огнетермостойких металлизированных материалов с пленочным покрытием возникают повреждения металлизированного слоя и тканой основы. В процессе эксплуатации происходит постепенное увеличение размера отверстий от прокола иглы в местах ниточного скрепления, в результате чего между боковой поверхностью поры огнетермостойкого металлизированного материала и переплетением швейных ниток образуются зазоры, способствующие переносу влаги и теплоты.

Специальная защитная одежда, изготовленная из указанных материалов, предназначена для ликвидации последствий чрезвычайных ситуаций и проведения аварийно-спасательных работ непосредственно вблизи или в очаге пожара. Несущественное и незаметное при визуальном осмотре повреждение огнетермостойкого металлизированного материала в околошовной зоне и последующая раздвижка нитей в швах не является индикатором очевидных повреждений, но может привести к преждевременному отказу готового изделия во время его использования.

Для исключения возможных отказов специальной защитной одежды пожарных необходим всесторонний контроль, включающий исследование динамики изменения теплозащитных свойств огнетермостойкого металлизированного материала верха на неповрежденных участках и в местах соединения деталей, то есть в швах.

В настоящее время известен ряд работ российских и зарубежных ученых, посвященных исследованию теплозащитных свойств материалов (пакетов материалов). Однако теоретических исследований, описывающих механизм переноса теплоты через околошовные участки одежды, устанавливающих влияние размеров пор на изменение теплозащитных свойств готовых изделий, не существует.

Целью данной работы является математическое моделирование процесса переноса теплоты через неповреждённые участки околошов-ной зоны одежды специального назначения в условиях нестационарной теплопроводности на базе применения метода сеток. Полученная математическая зависимость будет являться исходной для исследования и визуализации процесса переноса теплоты через перфорированные иглой швейной машины участки одежды специальной защитной пожарных от повышенных тепловых воздействий тяжелого типа (далее ОСЗ ПТВ Т) в условиях нестационарной теплопроводности.

В работах российских и зарубежных исследователей решение задач теплопроводности в многослойных текстильных материалах (пакетах материалов) реализовано преимущественно с использованием классических методов расчёта

(метода разделения переменных, операционного). Однако получение точного аналитического решения применительно к процессу нагрева (охлаждения) текстильного многослойного материала зачастую связано с трудностью адекватного описания граничных условий, которые не всегда однозначны.

В реальных условиях ликвидации чрезвычайных ситуаций при воздействии высоких температур, интенсивного теплового излучения между источником теплоты и огнетермостойким металлизированным материалом происходит теплообмен, включающий: 1) сложный теплообмен между источником и внешней поверхностью огнетермостойкого металлизированного материала; 2) теплопроводность в огнетермостойком металлизированном материале; 3) конвективную теплоотдачу от внутренней поверхности огнетермостойкого металлизированного материала к внутреннему слою воздуха.

Cложный теплообмен, протекающий между источником и внешней поверхностью огнетермостойкого металлизированного материала, является результатом совместного действия конвекции и лучеиспускания. В данном случае огнетермостойкий металлизированный материал расположен в непосредственной близости к источнику излучения, соответственно плотность теплового потока, подводимого к внешней поверхности огнетермостойкого металлизированного материала ( q₁ ), определена без учета конвективной составляющей, так как основная часть теплоты передается лучеиспусканием. Расчёт лучистой составляющей теплообмена между источником и внешней поверхностью огнетермостойкого металлизированного материала подробно рассматривался ранее в [1]. Формула для определения плотности теплового потока, подводимого к внешней поверхности огнетермостойкого металлизированного материала, записана в виде выражения:

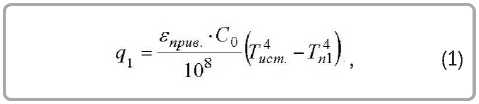
где C0 – коэффициент излучения абсолютно черного тела, Âò/(ì2·К4); Tèñò. – температура источника, которая в данном случае равна температуре среды (Tc1) со стороны внешней поверхности огнетермостойкого металлизированного материала, К; Tï1 – температура на внешней поверхности огнетермостойкого металлизированного материала, К; εприв. – приведенная поглощающая способность системы, определяемая по формуле:

,

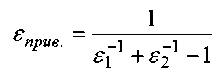
где ε ₁ – степень черноты источника излучения; ε ₂ – степень черноты поверхности исследуемого огнетермостойкого металлизированного материала.

Зависимость для определения плотности теплового потока, отведенного от внутренней поверхности огнетермостойкого металлизированного материала ( q₂ ) путем конвективной теплоотдачи была получена экспериментально, так как получить аналитическую зависимость, которая бы учитывала влияние всех факторов (объема пространства, физических свойств среды и т. п.), возникающих при проведении эксперимента в лабораторных условиях, не представляется возможным:

^₂ = 16 exp [0,085АТ_6И ] ,

где ∆ T_вн. – изменение температуры на внутренней поверхности материала, К , определяемое по формуле:

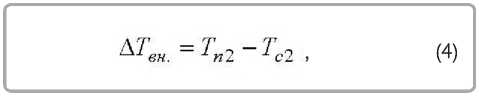
где T_ï2 – температура на внутренней поверхности огнетермостойкого металлизированного материала, К ; T_ñ2 – температура среды со стороны внутренней поверхности огнетермостойкого металлизированного материала, К .

При проведении работ вблизи источника теплового излучения происходит постепенное нагревание огнетермостойкого металлизированного материала, то есть имеет место процесс переноса теплоты внутри твердого тела при нестационарном режиме.

В настоящее время существует множество различных численных методов расчёта теплопроводности, которые дают хорошее приближение к решению задач, трудноразрешимых при помощи аналитических методов. Из численных методов решения задач теплопроводности в настоящее время наиболее широко используется метод конечных разностей (метод сеток) [2].

Решение поставленной задачи методом конечных разностей сводится к разбиению огнетермостойкого металлизированного многослойного материала на элементарные объемы, как показано на рисунке 1, с выделением опорных узловых точек: 1 – на границе «воздух – металлизированный слой»; 2 – внутри расчетной области «металлизированный слой»; 3 – на границе «металлизированный слой – слой полимерной пленки»; 4 – внутри расчетной области «слой полимерной пленки»; 5 – на границе «слой полимерной пленки – слой стекловолокна»; 6 – внутри расчетной области «слой стекловолокна»; 7 – на границе «слой стекловолокна – воздух».

Должно выполняться равенство:

4i = 42 + 4н ». , где днж - тепловой поток на нагрев огнетермостойкого металлизированного многослойного материала за время (т), Bm/w2:

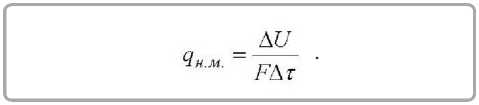
Расход теплоты (AQb№) на нагрев огнетермостойкого металлизированного многослойного материала, Дж:

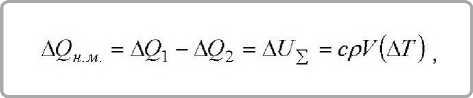
где A T - разность температур между внешней и внутренней поверхностью огнетермостойкого металлизированного материала за время ( τ ), К .

Для разработанной модели приняты следующие обозначения: A Q 1 - количество теплоты, подведенное к наружной поверхности огнетермостойкого металлизированного материала при нагревании, Дж ; A Q₂ - количество теплоты, отведенное от внутренней поверхности огнетермостойкого металлизированного материала при нагревании, Дж ; 6 1 , 6 2 , 6 3 - соответственно, толщина металлизированного слоя, слоя полимерной плёнки, слоя тканой основы огнетермостойкого металлизированного материала, № ; λ ₁ , λ ₂ , λ ₃ – соответственно, коэффициенты теплопроводности металлизированного слоя, слоя полимерной плёнки, слоя тканой основы огне-

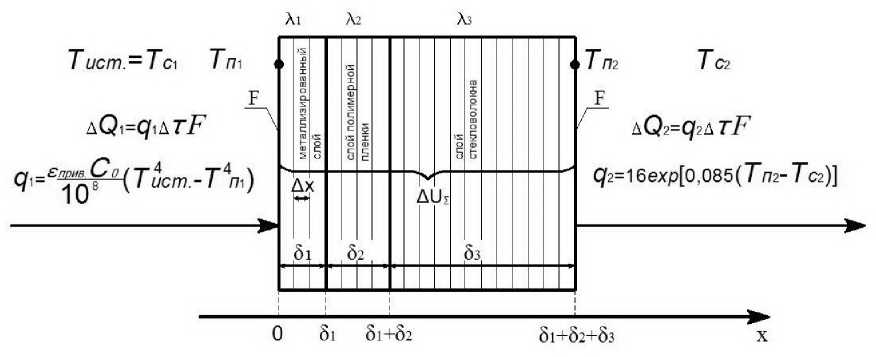
Рисунок 1 – К выводу уравнения для расчета температуры и плотности теплового потока в огнетермостойком металлизированном материале методом конечных разностей

термостойкого металлизированного материала, Вт/м·ºК ; ∆ U _∑ – суммарное изменение внутренней энергии огнетермостойкого металлизированного материала, Äæ ; ∆ x – элементарный шаг между узлами решетки, ì ; τ –время, ñ ; F – площадь огнетермостойкого металлизированного многослойного материала, ì² .

Максимально точное решение поставленной задачи возможно в случае, если величина элементарного шага стремиться к нулю, что позволяет базовую формулу для расчета теплового потока и дифференциальное уравнение теплопроводности Фурье аппроксимировать разност-

2 ∆ U₄(x_i, τ ) – изменение внутренней энергии внутри расчетной области «слой полимерной пленки»; ∆ U₅( δ ₁+ δ ₂, τ ) – изменение внутренней энергии на границе «слой металлизированной пленки – слой стекловолокна»; 2 ∆ U₆(x_i, τ ) – изменение внутренней энергии внутри расчетной области «слой стекловолокна»; ∆ U₇( δ ₁+ δ ₂+ + δ ₃, τ ) – изменение внутренней энергии на границе «слой стекловолокна – воздух» при наличии отведенного от внутренней поверхности потока q² ; x_i = ∆ x·i – координата i -ой узловой точки, ì ; n₁ – количество узловых точек в первом слое материала, определяемое по формуле:

м·ºК ; q – плотность теплового потока, Âò/     n₃ – суммарное количество узловых точек в ма-

ì² ; а – коэффициент температуропроводности, териале, определяемое по формуле:

ì²/ñ .

Для указанных элементарных объемов суммарное изменение внутренней энергии всей системы рассматривается как суммарное изменение внутренних энергий в каждом из перечис- ленных объемов:

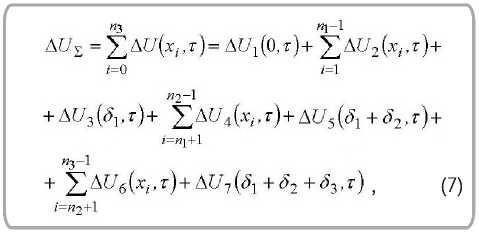
где ∆ U₁(0, τ) – изменение внутренней энергии на границе «воздух – металлизированный слой» при наличии подводимого к наружной поверхности потока q₁ ; £ ∆ U₂(x_i, τ ) – изменение внутренней энергии внутри расчетной области «металлизированный слой»; ∆ U₃( δ ₁, τ ) – изменение внутренней энергии на границе «металлизированный слой – слой полимерной пленки»;

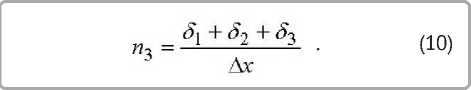
Согласно закону сохранения энергии, с уче- том уравнения (5), изменение внутренней энергии (∆U1) при наличии подводимого теплового потока (q1) определяется по формуле:

AU ! (O. r) = AQy - AQ^Ax, r)= q^FAr - q^Ax, тУАт =

• - 91 /tl         pAr =           + ДАг .

Ax            ( Ax Xy)

Изменение внутренней энергии ( ∆ U ) в любой точке огнетермостойкого металлизированного материала определяется выражением:

AU = срАУАТ ,          (12)

где c – массовая теплоемкость слоя огнетермостойкого металлизированного материала, êÄæ/ (кг-^оК) ; р - плотность слоя огнетермостойкого металлизированного материала, кг/м³ ; А V -элементарный объем, ì³ :

расчетной области «металлизированный слой», определяется выражением:

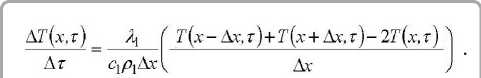
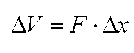
Алгебраические преобразования выражения (12), позволяют определить изменение температуры во времени по формуле:

В соответствии с выражением (16) изменение внутренней энергии для узловой точки, лежащей на границе расчетной области «металлизированный слой – слой полимерной пленки», будет иметь вид:

г

АГ _ АС/ АС/ Аг сутХГАг cpkxNT

Изменение температуры наружной поверхности огнетермостойкого металлизированного

материала во времени определяется c использованием закона теплопроводности Фурье [4] и зависимости (14), по формуле:

Ас ) (18)

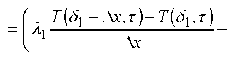
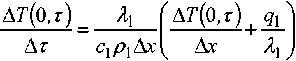
где c₁ – удельная массовая теплоемкость металлизированного слоя огнетермостойкого металлизированного материала, кДж/(кг-^оК ); ρ₁ – плотность металлизированного слоя огнетермостойкого металлизированного материала, кг/м³ .

Аналогично (11) выражение для определения изменения внутренней энергии для узловой точки, лежащей внутри расчетной области «металлизированный слой», имеет вид:

Для определения неизвестной температуры узловых точек, лежащих на границе (стыке слоев материала), необходимо рассчитать приведенные значения теплоемкости и плотности. Величина приведенной теплоемкости определяется по формуле:

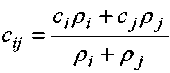
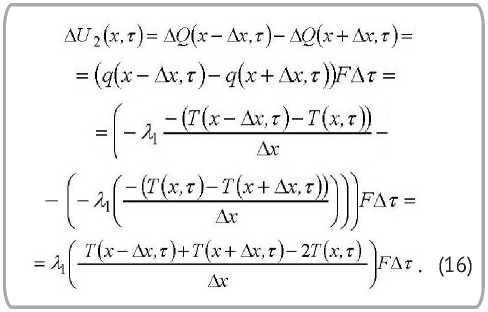
где c_ij – приведенная массовая теплоемкость узловой точки, лежащей на стыке i -го и j -го слоев огнетермостойкого металлизированного материала, кДж/(кг - °К) ; c i - удельная массовая теплоемкость i -го слоя огнетермостойкого металлизированного материала, кДж/(кг • °К) ; c_j – удельная массовая теплоемкость j -го слоя огнетермостойкого металлизированного материала, кДж/(кг°К) ; p i - плотность i -го слоя огнетермостойкого металлизированного мате-риала, кг/м³ ; P j - плотность j -го слоя огнетермостойкого металлизированного материала, кг/м³ .

Приведенная плотность огнетермостойкого металлизированного материала ( ρ_ij ) рассчитывается по формуле:

Аналогично уравнению (15) неизвестная температура для узловой точки, лежащей внутри

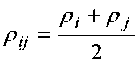
Аналогично выражению (17) неизвестная температура для узловой точки, лежащей на границе «металлизированный слой – слой полимерной пленки» будет иметь вид:

Расчет изменения внутренней энергии и температуры внутри расчетных областей «слой полимерной пленки», «слой стекловолокна» ( A U₄(x, t ), A U₆(x, t ) ) аналогичен расчету изменения внутренней энергии и температуры для узловой точки, лежащей внутри расчетной области «металлизированный слой» ( A U₂(x, t ) ), поэтому далее подробно не рассматривается.

Расчет изменения внутренней энергии и температуры на границе «слой металлизированной пленки - слой стекловолокна» ( A U₅( S j + S ₂, t ) ) аналогичен расчету изменения внутренней энергии и температуры для узловой точки, лежащей на границе расчетной области «металлизированный слой – слой полимерной пленки» ( A U₃( 8 j , t ) ), поэтому далее подробно не рассматривается.

Согласно закону сохранения энергии количество теплоты, отведенное с внутренней поверхности огнетермостойкого металлизированного материала, определяется выражением:

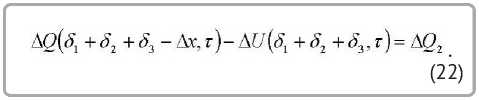
Тогда расчет изменения внутренней энергии на границе «слой стекловолокна – воздух» при наличии отведенного от внутренней поверхности потока ( q₂ ) выполняется по формуле:

АР_? (^ + g + З₃ , г) = -АД + АО(< + 8_г + ^ - М г) = = -q_гF^ г + q^ + S₂ + 5₃ - Ar, r)FA г =

.       (23)

Ц           Ас ) ■       4 '

В соответствии с выражением (17) формула для определения неизвестной температуры для узловой точки, лежащей на границе «слой стекловолокна – воздух», будет иметь вид:

После преобразования выражения (7) с учетом выражений (11), (16), (17), (23) получена расчетная формула (25) для определения внутренней энергии огнетермостойкого металлизированного материала в условиях нестационарной теплопроводности (при нагреве):

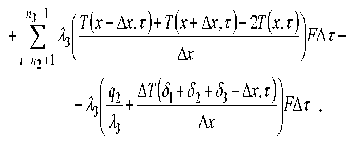
Согласно закону сохранения энергии, изменение внутренней энергии огнетермостойкого металлизированного материала определяется выражением:

.           (26)

Тогда расчетную формулу (25) можно записать в виде выражения:

qp! Ax

Ci Pi Ax

-3

c3p3Ax^3

Ax t4 ыЖ q2 ^Т{3у + 52 + §3- Ax, r)

СзА^к ^3

г^,г)-^ +Мт

Tta + J₇ - Ac, г

^c₂p₂ + C3P3 )Ax

мрив.

81 =-----s

1      108

q₂=^ exp [0,085 (т_п2 - T_c2)].

Таким образом, применение численного интегрирования, основанного на методе конечных разностей и методе тепловых балансов, позволяет представить расчет нагрева огнетермостойкого металлизированного материала в виде системы уравнений (28). Многократное повторение решений системы (28) с применением средств автоматизированного вычисления позволяет моделировать и последовательно воспроизводить процесс нагрева огнетермостойкого металлизированного материала.

Система уравнений (28) описывает процесс переноса теплоты через огнетермостойкий металлизированный материал, состоящий из трех слоев. Однако анализ зависимостей, составляющих данную систему, позволяет записать выражение для расчета температуры и плотности теплового потока на внутренней поверхности металлизированного многослойного материала (пакета материалов) в условиях нестационарной теплопроводности для любого количества слоев в виде системы уравнений:

с возможностью визуализации процесса переноса теплоты через огнетермостойкий металлизированный материал. Исходные данные, результаты теоретических исследований, внешний вид интерфейса программы представлены на рисунке 2.

где A T i (x) - изменение температуры огнетермостойкого многослойного металлизированного материала за время ( т ), К ; X i - коэффициент теплопроводности i -го слоя огнетермостойкого металлизированного материала, Вт/м·ºК ; S i - толщина i -го слоя огнетермостойкого металлизированного материала, № ; X_n - коэффициент теплопроводности n -го (последнего) слоя огнетермостойкого металлизированного материала, Вт/м • °К ; c_n - удельная массовая теплоемкость n -го (последнего) слоя огнетермостойкого металлизированного материала, кДж/ (кг^,0К) ; р_п - плотность n -го (последнего) слоя огнетермостойкого металлизированного материала, кг/м³ .

Полученные математические зависимости предполагают обработку большого массива данных. Поэтому для реализации расчетов разработан специализированный программный продукт

Для оценки результатов теоретических исследований в испытательной лаборатории учреждения «Научно-исследовательский центр Витебского областного управления МЧС Республики Беларусь» определены экспериментальные значения изменения температуры и плотности теплового потока на внутренней поверхности огнетермостойкого металлизированного материала торговой марки «Аlfa-Maritex» (стекловолокно, 100 %, поверхностная плотность 460±10 г/м² ) при плотности теплового потока, падающего на пробу 40 кВт/м² в течение 120 с . Испытания проводились согласно СТБ 1972-2009 (п. 9.26, стр. 11) при температуре окружающей среды 22±1 °C [5]. Сопоставление значений расчётных и экспериментально определённых температуры и плотности теплового потока на внутренней поверхности огнетермостойкого металлизированного материала представлены в таблице 1.

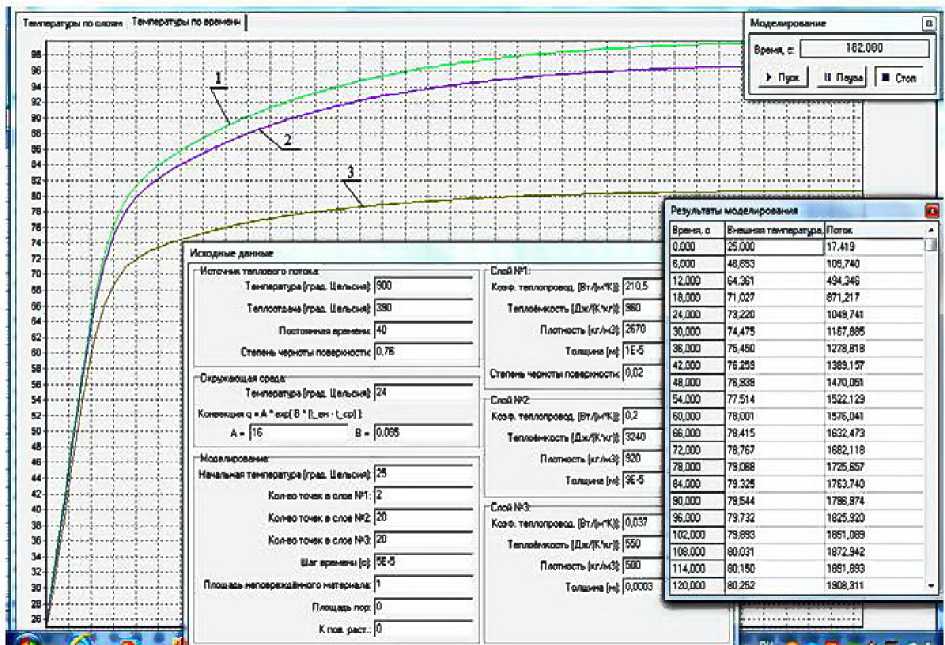
1 – графическая зависимость изменения температуры от времени на границе «металлизированный слой - слой полимерной пленки» ( δ ₁ ); 2 – графическая зависимость изменения температуры от времени на границе «слой полимерной плёнки – слой стекловолокна» ( δ ₁ + δ ₂ ); 3 – графическая зависимость изменения температуры от времени на внутренней поверхности слоя тканой основы из стекловолокна ( δ ₁ + δ ₂ + δ ₃ )

Рисунок 2 – Исходные данные, результаты теоретических исследований и внешний вид интерфейса программы для определения температуры и плотности теплового потока на внутренней поверхности огнетермостойкого металлизированного многослойного материала

Анализ таблицы 1 показывает, что в диапазоне 24<τ≤120 относительная погрешность результатов теоретических и экспериментальных исследований температуры и плотности теплового потока на внутренней поверхности неповрежденного участка огнетермостойкого металлизированного материала не превышает 7 %, что говорит о хорошей сходимости результатов и адекватности построенной математической зависимости. В диапазоне 0<τ≤24 относительная погрешность результатов теоретических и экспериментальных исследований указанных параметров превышает 7 %, что объясняется не- возможностью учета всех факторов, влияющих на процесс теплообмена в реальных условиях.

ЗАКЛЮЧЕНИЕ

С использованием метода конечных разностей получена математическая зависимость процесса переноса теплоты через неповреждённые участки огнетермостойкого металлизированного материала, используемого при изготовлении наружного защитного слоя ОСЗ ПТВ Т, в условиях нестационарной теплопроводности. Разработан программный продукт, позволяющий моделировать, последовательно воспроизводить процесс нагрева и определять температуру и плотность

Таблица 1 – Результаты экспериментальных и теоретических исследований температуры и плотности теплового потока на внутренней поверхности огнетермостойкого металлизированного материала «Alfa-Maritex» (волокнистый состав - стекловолокно, 100 %, поверхностная плотность 460±10 г/м2) Время воздействия, т, с Температура на внутренней поверхности, t, °C Плотность теплового потока на внутренней поверхности, q2, кВт/м2 экспериментальная расчетная (модель 28) экспериментальная расчетная (модель 28) 1 2 3 4 5 0 25 25 0,22 0,02 6 44 46,7 0,37 0,11 12 54 64,4 0,62 0,49 18 59 71,0 0,86 0,87 24 65 73,2 1,05 1,05 30 70 74,5 1,24 1,17 36 72 75,5 1,37 1,28 42 75 76,3 1,49 1,39 48 76 76,9 1,57 1,47 54 79 77,5 1,63 1,52 60 81 78,0 1,68 1,58 66 82 78,4 1,72 1,63 72 83 78,8 1,78 1,68 78 84 79,1 1,83 1,73 84 84 79,3 1,85 1,76 90 85 79,5 1,86 1,80 96 85 79,7 1,86 1,83 102 86 79,9 1,88 1,85 108 86 80,0 1,89 1,87 114 86 80,2 1,89 1,89 120 86 80,3 1,89 1,91 теплового потока на внутренней поверхности огнетермостойкого металлизированного материала в любой момент времени. Проведённые теоретические исследования показали хорошую сходимость результатов с экспериментальными данными, что подтверждает адекватность полученной математической зависимости и возможность её дальнейшего использования в качестве базовой для исследования процесса переноса теплоты через перфорированные иглой швейной машины участки околошовной зоны ОСЗ ПТВ Т в условиях нестационарной теплопроводности.