Моделирование процесса пиролиза прямогонного бензина с использованием генетического алгоритма

Пиролиз углеводородного сырья - важный источник для производства олефинов и ароматических соединений, являющихся основой нефтехимической промышленности. Задачи оптимизации процесса высокотемпературного пиролиза углеводородов, представленные в работе, направлены на достижение максимального выхода целевых продуктов пиролиза и связаны с определением оптимальной совокупности режимных параметров печи.

Разработанная математическая модель узла пиролиза учитывает взаимосвязь протекающих в реакторе физических процессов – гидродинамических, тепловых, массопередачи, с уравнениями химической кинетики. Принимается, что в качестве сырья для пиролизного реактора используется прямогонный бензин, все компоненты, участвующие в реакциях, находятся в газовой фазе, а змеевик пиролизной печи является реактором идеального вытеснения, в связи с высокой турбулентностью потока реагентов.

Для описания химизма процесса предложена кинетическая схема, состоящая из первичной реакции разложения углеводородного сырья, рассмотренной в [1], и вторичных элементарных химических реакций:

• 1.    Naphtha. = 0.5H 2 + 0.76CH 4 + 1.16C 2 H 4 + 0.13C 2 H 6 + 0.38C 3 H 6 + 0.09C 3 H 8 + 0.008C 4 H 10 0.245C 4 H 8 + 0.113C₄H₆ + 0.08С +

• 2.    C₂H₄ ~ C 2 H 2 + H₂

• 3.    C₂H₆ ~ C₂H₄ + H₂

• 4.    C 3 H 8 ~ C₃H₆ + H₂

• 5.    C 4 H 8 ^ C 4 H 6 + H 2

• 6.    C₄H₁₀ ~ C₄H₈ + H₂

• 7.    C 4 H 10 ^ 2C 2 H 4 + H 2

• 8.    C₃H₆ ~ C 2 H 2 + CH₄

• 9.    2C 2 H₆ ^ C 3 H 8 + CH₄

• 10.    C 3 H 8 ^ C₂H₄ + CH₄

• 11.    C₄H₈ ^ C₂H₄ + C₂H₄

• 12.    C₄H₁₀ ^ C₃H₆ + CH₄

• 13.    C 4 H 10 ^ C 2 H 4 + C 2 H 6

• 14.    2C₃H₆ ^ 3C₂H₄

• 15.    C₃H₆ + H₂ ~ C₂H₄ + CH₄

• 16.    C₄H₈ + H₂ ~ C₃H₆ + CH₄

  17. C 2 H 2 + C 2 H 4	^C 4 H 6
  18. C 2 H 6 + C 2 H 4	^ C3H6 + CH4
  19. C 3 H 8 + C2H4	^ C 3 H 6 + C 2 H 6
  20. C 3 H 6 + C 2 H 6	^ C4H8 + CH4
  21. C2H4 + C4H6	^ B + 2H 2
  22. C 3 H 6 + C 4 H 6	^ T + 2H 2
  23. C 4 H 8 + C 4 H 6	^ EB + 2H 2
  24. C4H6 + C4H6	^ ST + 2H 2

• 25.    T + H₂^B + CH₄

• 26.    EB + H₂ ^ T + CH₄

• 27.    C₄H₈ + CH₄ ^ C₂H₄ + C 3 H 8

• 28.    C₄H₆ + CH₄ ^ C₃H₆ + C₂H₄

• 29.    CH₄ + CH₄ ^ C₂H₄ + 2H 2

где B - бензол, T - толуол, EB - этилбензол, ST - стирол, С⁺ - углеводороды в составе которых больше 4 атомов углерода.

Система включает в себя 29 прямых элементарных молекулярных реакций и 10 обратных, протекающих между 15 продуктами. В работе принято, что константы скоростей химических реакций имеют Аррениусовскую зависимость от температуры:

Ei(T)

K(T)i = Ui • exp R-T(L),

rgei = 1..39, ^(T). - константа скорости i-ой реакции схемы (с-1, м3/(моль*с)), U. - пред-экспоненциальный множитель i-ой реакции схемы (с-1, м3/(моль*с)), R - газовая постоянная (Дж/(моль*К), E; - энергия активации i-ой реакции схемы (Дж/моль), L - текущая точка по длине змеевика, T - температура пирогаза (К).

С целью уменьшения размерности задачи в работе проводится оценка энергий активации по правилу Поляни-Семёнова [2], описывающему соотношения между энтальпией элементарной реакции и энергией активации:

Для экзотермических реакций:

Е;(Т)=А—0.25^Н;(Т),

Для эндотермических реакций:

Е ; (Т) = A + 0.75^H ; (T), где H ; - изменение энтальпии i-ой элементарной химической реакции   (Дж/моль),

А = 48 (кДж/моль) для реакций отрыва атома и замещения, А = 42 (Дж/моль) для реакций присоединения.

Для расчета тепловых эффектов реакций применяется уравнение Кирхгофа:

H_t(T),= ДН₄(Т н ) + ^/XCp_m g. (TW, где Cp_HHg. - индивидуальные теплоемкости компонентов, входящих в   i-ую реакцию

(Дж/(моль*К)), знак Д обозначает разность между продуктами и реагентами i-ой реакции с учетом стехиометрических коэффициентов, Т_к – температура смеси в текущей точке разбиения змеевика (К), T_H - температура смеси в предшествующей точке (К).

CP uHgj T) = Д_к + B_kT(L) + C_kT²(L) + O_kT³(L), где Д к , B k , C k , D k - константы в уравнении идеально-газовой теплоемкости для k-ого компонента схемы.

На основе кинетической схемы составлен материальный баланс, описываемый системой обыкновенных дифференциальных уравнений первого порядка:

dF_k                 л P(L) л d_BH²

^г=|2(^(Т«^]^г где к = 1..15; i = 1. .39, Fk - мольный расход компонентов пирогаза (моль/с), s^k - стехиометрический коэффициент молекулярной реакции, P - давление в текущей точке змеевика (Па), dвн — внутренний диаметр змеевика (м).

В систему входят 39 неизвестных параметра - по числу предэкспоненциальных множителей в уравнении Аррениуса (1).

Тепловой баланс процесса описывается дифференциальным уравнением следующего вида:

d‘ р ■ а(Т) ■ л ■ d dL = (G + G_py Ср(Т)

( Т ст (Т) - T(L))

G

(G + G p ) ■ Ср(Т)

■^№(Т) • x_vl(L)_k), к=1

где ф - коэффициент неравномерности обогрева, а(Т) - коэффициент теплоотдачи от стенки змеевика к движущемуся потоку (Дж/(с*К*м²), d - наружный диаметр змеевика (м), Ср(Т) - теплоемкость реакционной смеси (Дж/(кг*К)), G и G p - расход сырья и пара соответственно (кг/с), x_vl - мольные доли влажных компонентов пирогаза, Т_ст(Т) - температура стенки змеевика (К).

^mo^^md(L) k

x_vl(L)k = ------—----------

Gp ■ md(L)k + mo ■ G где m0 и mk - молекулярные массы воды и кого компонента соответственно, md - мольные доли компонентов пирогазовой смеси.

md(L)_k =

F(L) k S i=i F(L)_t

Для расчета уравнения (2) оценка термодинамических параметров осуществлена с использованием следующих зависимостей:

а(Т)

^вн __■   ^ст  I ^R ,

№(ТуЛ(Т) + Лст + Лк где ^u(T) - критерий Нуссельта, Л - теплопроводность пирогазовой смеси (Дж/(м*с*К)), 5ст - толщина стенки (м), 5к - толщина отложений кокса (м), Лст - теплопроводность материала трубы (Дж/(м*с*К)), Лк - теплопроводность кокса (Дж/(м*с*К)).

^м(Т) = 0.0214 ■ Ре(Т)0.8 ■ Pr(T)0.4, где Не(Т) - критерий Рейнольдса, Рг(Т) - кри терий Прандтля.

Ке(Т) =

^(ТМвн.!^ м^(Т) ■ д '

где г(Т) - скорость потока пирогаза (м/с), р - плотность пирогаза (кг/м³), ^(Т) - динамическая вязкость пирогазовой смеси (кг*с/м²), д - ускорение свободного падения (м/с²).

Рг(Т) =

д • д(Т)^ Ср(Т)

Л(Т)      ,

Скорость потока пирогаза рассчитывается по формуле [3]:

У_aP о T(L)(m о G + G p E k=1 m k md(L) k ) ЩТ) = ----------------- т^ -----------------,

STоP(L)mо Ek=imkmd(L)k где 1^ - молярный объем газов при нормальных условиях (л/моль), Ро и То - нормальные условия (Па и К соответственно), 5 - площадь сечения трубы (м2).

Теплоемкость пирогазовой смеси описывается зависимостью:

G p 5 r=i m k md ⁽ L) k + m o G

^p ^ m k md ⁽ L) k (сР инд₀⁽ Т)) +

0 k=1  15

V md(L)k ^(^^■(^CD)/ где Сринд , - индивидуальная теплоемкость водяного пара (Дж/(моль*К)).

Сринд0(Т) = Ло + ВоТ(Ь) + СоТ2(£) + РоТ3(£), где Ло, Во, Со, D0 - константы в уравнении идеально-газовой теплоемкости для водяного пара.

Вязкость индивидуального компонента пирогазовой смеси рассчитывается по уравнению Чэмпена-Энскога с использованием потенциала Леннарда-Джонса [4]:

Р инд _к ^(Т)

26.69 ■

7mк/T(Z2

«Мк ,

где о - радиус твердой сферы (м), П - интеграл столкновений.

_ 2,3551 — 0,0874 ■ щ°=   (^   ,

7С где Рс, Тс - критические давление и температура (Па, К), щ - фактор ацентричности.

1.16145   0.52487

^П _T0.14874 ⁺ _0.7732^T _pot ‘ pot        ^е

,  2.16178

⁺ _е 2.43787■7’p _Ot ^,

где ‘pot - потенциальная температура.

Т^.

где £ - параметр потенциала Леннарда-Джонса

£ = (0,7915 + 0,1693 • ш) • Т_с,

Для расчёта вязкости полярной молекулы воды (3) интеграл столкновений (4) пересчитывается по уравнению Брокау:

0.2 * 52

^Н2О П ' У------, potH2O где 5 - параметр полярности молекулы.

Теплопроводность    индивидуального компонента пирогазовой смеси рассчитывается по методу Мисика и Тодоса:

Л инд_к (Т) = 4,45 • Ю"⁶ • Т^

Ср индк • ^Рс / к • -------------------------------------------------------------

^Тс ^1/6_к •m¹ /²/

где Тг - приведенная температура.

т _ T(L)

^Т Гк     _Т ,

^Тс к

Зависимость (5) справедлива для метана, нафтенов и ароматических углеводородов, во всех остальных случаях применяется выражение:

Я инд_к = 10 - ⁶ • (14,52 • Т_Г к - 5,14)^2/3 •

Ср_ИН д _к • ^Рс / к

Т с/⁶ _k^m 1f2 _к’

Вязкость всей смеси c учетом пара определяется по уравнению Васильевой [4]:

^у 1 " М инд^

^м=2 1=1

У1⁶ v- -А- ’

Ь]=1У] ^A i,j

где у - мольные доли компонентов смеси и пара, A i,j - параметр уравнения Вильке:

(1 + ( ^ ^инд ! )^1/2 • ( ^2 )^1/4)^1/2

Минд ;         ^1

Av V = -----------=------------

]          (8 • (1 + -)   ':

Для определения теплопроводности смеси пирогаза с учетом пара проводятся аналогичные вычисления.

Для вычисления температура стенки в зависимости (2) используется уравнение:

Т ст (Т)⁴ +      • Т_ст(Т) - Т_т⁴ - -^- • T(L) = 0,

Ут И                ^ст И где ут - параметр, учитывающий зачернен-ность поверхности трубы, И - коэффициент, учитывающий интенсивность теплообмена между источником нагрева и участком трубы,

Тт - температура в топке печи (К).

а2

И У6 iF

^ z=1 ¹ горелки

•2

Z = 1

F

1 горелки

а² + (г - ^Z) 2 ,

X 1дм    6/

где ргорелки - расход топлива в горелках (кг/с), /зм - длина змеевика (м), а - настроечный параметр.

Дифференциальное уравнение описывающее изменение давления по длине змеевика имеет вид:

dP Р станд / 5(Р 9 \ У + МГО dL d_B H ⁴ • Т станд ⁽ ^ вн 1 дм ) ^ « смеси (L) • P(L)

где Рстанд и Тстанд - нормальные давление и температура соответственно (Па, К), 6(T) - коэффициент гидравлического трения потока о стенки змеевика, р - коэффициент местного сопротивления калача змеевика, Мсмеси - средняя мольная масса смеси.

(Дст     68 \0'25

9(Т) = 0.11 • (— ст + —— )

\ ^ вн    Де^(Т)/

,

Дифференциальные уравнения кинетики, записанные с учетом теплового баланса и гидродинамики в совокупности, представляют полное математическое описание процесса пиролиза в змеевике печи.

Оценку предэкспоненциальных множителей U из уравнения (1) предложено проводить с помощью поискового алгоритма, так как данная задача имеет множество локальных экстремумов. На данный момент одним из предпочтительных способов многоцелевой оптимизации являются генетические алгоритмы, основанные на механизмах, аналогичных естественному отбору в природе. Поиск оптимального решения опирается на гипотезу селекции.

Генетический алгоритм [5], оперирует не искомыми переменными, а закодированными отображениями - хромосомами. В качестве функции цели используется модульный критерий отклонения расчетных значений от экспериментальных:

('25' | (^%к"^%“^рк⁾ |. 100) ^ _min

У к=11 | ^_е %Рк | У

Для корректной работы алгоритма с большим числом неизвестных параметров предложено его модифицировать. В работе применяется кодировка по Грею, что гарантирует соответствие соседних порядков хромосом с ближайшими декодируемыми точками пространства. Используется турнирная селекция, при которой все особи текущей популяции случайным образом разбиваются на подгруппы с последующим выбором в каждой из них особи с наилучшей приспособленностью, при этом повышение ранга турнира приводит к уменьшению числа итераций всего алгоритма, но снижению скорости вычислений. Применяется кроссовер с частичным случайным выбором аллелей. Данная схема, основанная на следующем правиле: совпадающие аллели родительских хромосом, сохраняются у потомков, а не совпадающие выбираются случайным образом. Этот прием позволяет увеличить поисковую способность генетического алгоритма. Задается высокая вероятность мутации хромосом, что обеспечивает широкие возможности перебора решений. Новая популяция создается на основе принципа эли-тизма. В данной работе выбрана его разновидность – конкурентный подход с глобальным состязанием, при которой все родительские особи "состязаются" со всеми потомками и победители, чья приспособленность выше, независимо от возраста, переходят в следующее поколение.

В качестве экспериментальных данных используются результаты промышленной эксплуатации пиролизной печи SRT-VI. Идентификация модели проводилась по выборке из 14 наборов выходов процесса пиролиза, полученных при различных технологических режимах. Часть из них представлена в таблице 1.

Т а б л и ц а 1

Данные промышленной эксплуатации печи SRT-VI

Продукт (% мас.) № эксперимента 1 2 3 4 5 H2 1.28 1.39 1.41 1.37 1.45 CH4 13.65 13.44 13.07 14.14 14.62 C2H4 29.4 28.97 27.44 29.55 30.46 C2H6 4.87 4.87 4.95 5.01 4.82 C3H6 18.2 18.42 20.14 17.68 17.37 C3H8 0.47 0.58 0.59 0.59 0.48 C4H10 0.23 0.23 0.24 0.2 0.19 C4H8 4.43 4.4 5.3 3.96 3.81 C4H6 7 7.53 78.01 7.26 6.75 C2H2 0.58 0.58 0.71 0.49 0.48 B 13.3 12.75 12.01 13.83 13.57 T 3.73 3.71 3.42 3.33 3.47 EB 1.4 1.51 1.41 1.2 1.25 S 1.52 1.62 1.3 1.4 1.54 Т (К) 1113 1108 1098 1118 1118 P_S 0.6 0.6 0.6 0.55 0.6 F_S 1540 1540 1540 1540 1540 где P_S – отношение пар/сырье, Т – температура на выходе из змеевика (К), F_S – расход прямогонного бензина (кг/ч).

Разработанная математическая модель процесса пиролиза позволяет получить профили концентраций продуктов пиролиза по длине змеевика (рисунок 1).

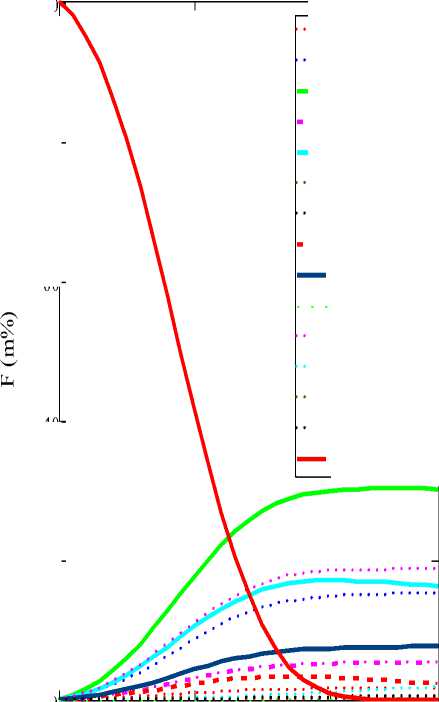
H2

CH4

C2H4

• •■ C2H6

C3H6

C3H8 C4H10

• ■ ■ C4H8

C4H6

C2H2

B

T

EB

S

NAPHTHA

L (m)

Рисунок 1. Профиль концентраций продуктов пиролиза по длине змеевика.

Профиль изменения температуры пирогазовой смеси по длине реактора представлен на рисунке 2.

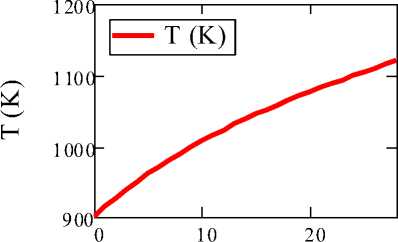
L (m)

Рисунок 2. Профиль изменения температуры пирогаза.

Профиль изменения давления реакционной смеси по длине змеевика отображен на рисунке 3.

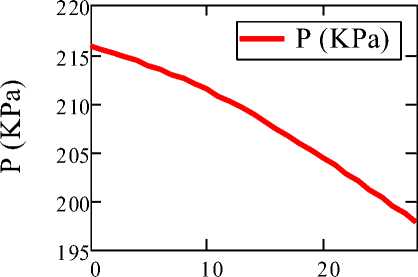
L (m)

Рисунок 3. Профиль изменения давления пирогаза.

Среднее расхождение полученных значений от экспериментальных данных не превышает 10 %, что соизмеримо с погрешностью хромотографии. В таблице 2 приведен анализ погрешностей целевых продуктов процесса: