Моделирование процесса распределения давления при проведении гидроразрыва пласта

Тюменский ГНГУ, г. Тюмень, Россия

ООО «Газпром добыча Уренгой, г. Новый Уренгой, Россия

ООО «РН- Юганскнефтегаз», г. Нефтеюганск, Россия

ООО «ЛУКОЙЛ» Западная Сибирь, г.Нижневартовск, Россия

Существуют неоднозначные мнения о возможности использования гидроразрыва пласта не только как метода интенсификации добычи углеводородов, но и как способа увеличения охвата пласта воздействием. Представляется необходимым выделить в этой проблеме два аспекта: чисто технологический и технико-экономический [15, 16, 17]. В технологическом плане, ГРП, прежде всего, рассматривают в качестве метода интенсификации притока и увеличения производительности скважин [10, 12, 14].

В то же время в сильно неоднородных и прерывистых пластах при соответствующих размерах «крыльев» трещин ГРП может обеспечить дополнительный охват пласта за счет подключения неохваченных дренированием пропластков и линз [11, 13]. Нередко в определенных случаях большеобъемный ГРП (с большой длиной «крыльев» трещины) может вызвать и уменьшение охвата пласта [1, 2, 5].

Для описания процесса ГРП имеется несколько типов моделей: аналоговые, физические и наиболее популярные - машинные модели, представляющие из себя несколько типов моделей. В процессе разработки программы для моделирования пласта применяют три вида моделей: математическую, численную и непосредственно машинную [3, 4, 9].

Математические модели составляются на основе нелинейных дифференциальных уравнений в частных производных с соответствующими начальными и граничными условиями. Численная модель представляет собой систему уравнений, полученную при аппроксимации сложных дифференциальных уравнений в пригодную для об- вокупность программ, составленная с целью решения численной модели.

Эксплуатация скважины в близи непроницаемой границы раздела относится к двумерным задачам фильтрации, то есть фильтрация флюида происходит в двух направлениях в горизонтальной плоскости. Уравнение для двухмерного течения имеет вид:

з2р з2р

Эх2 Зу2

где х, у - координаты в декартовой системе, Р - давление в пласте.

При решении данной задачи, пласт представляется неоднородным,    начальным условием является достижение постоянного давления, т. е. давление в декартовых координатах в момент закрытия скважины для записи КВД должно иметь известное распределение:

Р(л.у) = f, ⁽²⁾

при t=0. Граничными условиями восстановления давления при t>0 будут:

• 1)    на скважине с координатой M_c(x_c;y_c)

  

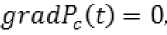
  т. е.

  
  

dP_c ^Р^ А

= и;-- = U; (3) ах ау

• 2)    на дальних границах (на бесконечном расстоянии) можно принять давление равным исходному пластовому, т.е.:

х > -да , Р(х)=Р пл , у ^ +да или у ^ -да , Р(у)= Р пл ;

• 3)    на границе (барьере)

gradP(x) = 0 dP(x) _n т. е. —:— — U;

• 4)    на трещине:

,

л ^^._л

• т. е. --- = U; ^—— — U.

dx dy

Таким образом, для решения данной задачи необходимо знать распределение давления в пласте перед остановкой скважины, т. е. Р(х, у) при t=0. Найти функцию Р(х, у), определяющую ста- ционарный процесс фильтрации для решения данной задачи, можно различными способами. По существу, необходимо решить задачу (1). Уравнение (1) – это уравнение Лапласа для стационарного течения. Очевидно, решением этого уравнения является следующее: при r=rc, или в точке Mc(xc;yc) и на трещине, давление должно быть равным забойному перед остановкой скважины, то есть . Это давление, обеспечивает приток в скважину.

Решить уравнение Лапласа можно многими способами, например, на основе классического конечно-разностного представления уравнения Лапласа с последующим решением матрицы – системы п- уравнений с четырьмя неизвестными. А само уравнение:

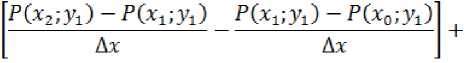
pCxi^D-pCxijyi)

- Ду

РСХ1У71)2^ыУо)

Ду .

при Лх=Лу получаем:

^(х2; У1) + /Чзд) + РСхпУг) + ^пУо) = WiJi)

Запишем систему п -уравнений, где их количество определится по числу выбранных ячеек при составлении сеточной модели.

Из множества других методов, на наш взгляд, предпочтительным является метод Зейделя, на основе которого простыми математическими процедурами можно осуществить итерационную настройку системы (давлений) в пространстве. Под итерацией понимается одно из ряда повторений математических операций, использующее результат предыдущей аналогичной операции. Данные повторения используют до тех пор, пока полученный результат не будет отличаться от предыдущего на определенную крайне малую величину.

Таким образом, расчет давлений в каждой ячейке P^k(x₁;y₁) при известных значениях P^k(x 0 ;y 1 ), P^k(x 2 ;y 1 ), P^k(x 1 ;y 0 ), P^k(x 1 ;y 2 ) будет происходить по формуле:

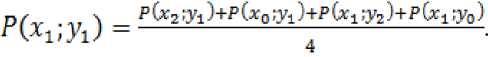
Так, установлено, что при достижении волны депрессии барьера профиль давлений теряет свою симметричную форму, что не учитывает метод воображаемой скважины, в котором профили давлений всегда симметричны, что в свою очередь влияет на форму кривой восстановления давления.