Моделирование процесса распылительной сушки суспензии протеинового зеленого концентрата (ПЗК)
Автор: Шевцов А.А., Дерканосова А.А., Коротаева А.А., Муравьев А.С.
Журнал: Вестник Воронежского государственного университета инженерных технологий @vestnik-vsuet
Рубрика: Процессы и аппараты пищевых производств
Статья в выпуске: 1 (63), 2015 года.
Бесплатный доступ
Разработка и внедрение высокотехнологичных и энергоэффективных способов производства кормов актуально и целесообразно в связи с тем, что предприятия не способны обеспечить рынок потребителей комбикормов высококачественными продуктами по доступным ценам. Для решения этой проблемы разработана ресурсосберегающая технология производства протеинового зелёного концентрата (ПЗК) из листостебельной массы высокобелковых растений. Наиболее энергоемким процессом получения ПЗК является распылительная сушка. При этом вопросы энергосбережения и получение продукта высокого качества решаются путем моделирования. Модель сушки, разработанная в данном исследовании, основана на убывающем фронте испарения, который используется во многих исследованиях сушки капель. Поставлена задача получить основные уравнения тепломассопереноса в периоды постоянной и убывающей скорости сушки. Предполагается также, что сушка проходит в периоды постоянной и убывающей скорости сушки. Для обоих периодов сушки получены основные уравнения тепломассопереноса. Изменение теплофизических характеристик определены статистическими методами в интервале значений влажности ПЗК 10-75 % и температуры 20-100 %. Модель решена методом конечных разностей с погрешностью результатов моделирования 12 %. Метод конечный разностей представляет собой численный метод решения дифференциальных уравнений, основанный на замене производных разностей схемами, является сеточным методом. Проведена идентификация параметров модели по экспериментальным данным, полученным на опытной распылительной сушильной установке. Решение математической модели позволяет определять изменение влажности (концентрации СВ) и температуры по радиусу капли в процессе распылительной сушки концентрата ПЗК, что необходимо как для выбора геометрических размеров сушилки, так и для управления технологическими параметрами сушки.
Кормопроизводство, протеиновый зеленый концентрат, распылительная сушка, математическое моделирование, уравнения тепломассопереноса
Короткий адрес: https://sciup.org/14040386
IDR: 14040386 | УДК: 66.047.4
Текст научной статьи Моделирование процесса распылительной сушки суспензии протеинового зеленого концентрата (ПЗК)
Главная цель развития кормопроизводства — увеличение объемов и улучшение качества кормов, в том числе и концентрированных.
В настоящее время отмечается значительный недостаток отечественного кормового белка. Для решения этой проблемы разработана ресурсосберегающая технология производства протеинового зелёного концентрата (ПЗК) из листостебельной массы высокобелковых растений [1, 2].
Наиболее энергоемким процессом получения ПЗК является распылительная сушка, от режимов которой в значительной степени зависят себестоимости и качества готового концентрата. Поиск оптимальных режимов процесса распылительной сушки в области допустимых технологических свойств высушиваемого продукта при минимальных энергетических затратах, как правило, достигается методами математического моделирования с последующей экспериментальной проверкой полученных результатов [3].
Известные модели основаны на углублении фронта испарения влаги в капле, с постепенной потерей влаги в процессе сушки [4, 5]. Однако они не учитывают особенности процесса распылительной сушки в периодах постоянной и убывающей скорости сушки с учетом специфических свойств ПЗК. При этом не детализируется алгоритм их решения, что не дает основания для их использования в систематических расчетах при поиске оптимальных режимов.
Цель работы – сформулировать задачи моделирования процесса распылительной сушки ПЗК в период постоянной и убывающей скорости сушки.
Период постоянной скорости сушки.
В периоде постоянной скорости сушки тепло передается конвекцией от окружающего воздуха к поверхности капли и вызывает испарение свободной воды пока она не будет полностью удалена (рисунок 1). Водяной пар с поверхности капли удаляется путем конвекции.
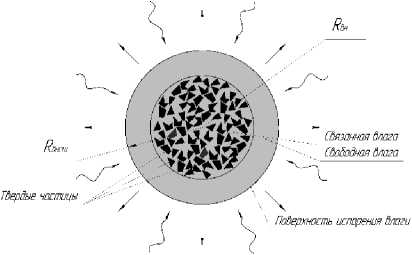
" Поток блооо
—-/ \-, Поток теплоты
Рисунок 1. Сушка капли в период постоянной скорости
Моделирование процесса сушки в первом периоде проводилось с учетом следующих упрощающих допущений:
-
1. Капли имеют сферическую форму.
-
2. Кондукция является механизмом передачи тепла внутри капли.
-
3. Внутренний радиус капли постоянен.
-
4. Удаление свободной воды на поверхности задается уменьшением внешнего радиуса капли.
-
5. Влажность, температура и скорость воздуха, окружающего каплю, постоянны.
-
6. Внутренней циркуляцией воды и капиллярными эффектами пренебрегается.
-
7. Отсутствует физическое или химическое взаимодействие между твердыми частицами и влагой.
-
8. Температура капли изменяется только в радиальном направлении.
-
9. На границе фронта испарения устанавливается состояние теплового и концентрационного равновесия.
-
10. Твердые частицы и влага вокруг них находятся в тепловом равновесии.
-
11. Изменение теплофизических характеристик определены методом Волькен-штейна [6] и обработаны в программе «STATISTICA 10» в интервале значений влажности ПЗК 10-75 % и температуры 273-373 K:
а х 10 8 = -7,15 х 10 -7 ? 3 - 9,54 х 10 -6 Т2РК + 1,14 х 10 —6П У 2 - 2,00 х 10 -5РК3 - 3,66 х 10 -4 ? 2
+ 4,88 х 10 -3 ГК - 9,76 х 10 -4 К 2 + 0,16 Г + 0,75К - 6
Л = -1,18 х 10-6 Г 3 - 1,17 х 10 -5 Г 2 К 2 - 9,18 х 10 -7 ТК 2 - 4,77 х 10 -7 К 3 + 7,71 х 10 -4 ? 2 + 6,81 х 10 -3 ГК + 2,53 х 10 -3 К 2 - 9,67 х 10 -2 Г - 0,95К - 11,13
с = -1,64 х 10-10 Г 3 - 1,64 х 10 -9 Г 2 К 2 - 1,41 х 10 -9 ТК 2 - 1,24 х 10 -10 К 3 + 1,15 х 10 -7 ? 2 + 9,91 х 10 -7 ГК + 3,43 х 10 -7 К 2 - 1,41 х 10 -5 Г - 1,31К - 1,53 х 10 -3
Принимая элемент дифференциального объема в области связанной влаги и учитывая тепловой баланс, получим уравнение переноса теплоты в виде:
V 0 < г < RBH, t > 0
д
Qt [£Р в с вГос + (1 ^)Р тст ? св ]
= -Л^-(г29св),
Г2 дг
где £ - объемная доля воды в области связанной влаги. Индексы в, т и св представляют свободную влагу, твердые вещества и область связанной влаги, соответственно.
Используя закон Фурье, уравнение (1) принимает вид:
д я. [£РвсвТсв + (1 ^)РтстТсв]
■1 дь дТ,; (2)
г2 дг V Л св дг )'
где Лсв - коэффициент теплопроводности, Вт/м-K, определяемый как:
где £в - удельная теплота парообразования, Дж/кг; «са - коэффициент конвективной теплопередачи, Вт/м2-К; Тса - температура сушильного агента, K.
Уравнение (8) получено путем использования теплового баланса на поверхности испарения Rвнеш(t) между теплом, передаваемым конвективно к поверхности капли и теплом, переданном кондуктивно из глубины капли для испарения некоторой части свободной влаги. После преобразования уравнения (8) получаем:
Ясв — £Лв + (1 — £)Ят
Уравнение (2) принимает окончательную форму:
где к
дТ д2Т 2дТ к1-^в —-Нв + --Гв, (4)
дt дг2 г дг
_ £рвсв + ( 1-£ ) Р т с т
R внеш
Ь в дt — к з (Т в где к3 — ^ са ; к4 — — .
3 Р в 4 Р в
— Тса ) + к4" д 7 . (9)
1 —
Л св
.
Для решения уравнения (4) приняты:
- начальное условие:
V 0<г
- два граничных условия в центре и на внутреннем радиусе капли:
V г — 0. t > 0 ^—Я(.в—— 0, св dr
V г —R вн ,t>0 ^ Т св —Т в
Принимая элемент дифференциального объема в области свободной влаги и учитывая тепловой баланс, уравнение теплопередачи для области свободной влаги представлено следующим образом:
Отслеживание движения границы Rвнеш(t) между свободной влагой и воздухом осуществляется уравнением баланса массы, в котором изменение массы капли равно конвективному потоку массы паров воды на границе фронта испарения: V г — R вн , t > 0
Р в ^^ неш ——6 см М в (С п
—
С са ),
где (Зсм - конвективный коэффициент массопе-реноса, м/с; М в - молярная масса воды, кг/моль; Сп и Сса - концентрации паров воды на поверхности капли и сушильного агента соответственно, моль/м3.
Сп в уравнении (10) определяется как:
= Рп(Т т ) п R cа Т т '
где:
V R вн < г < R, д г
внеш(t) , t 0 ^
д^. [рвСвТв]
1»,,
7 2 дГ Сг ’ в )'
дТв
’ в — —Яв" д7"
С учетом (5) и (6) уравнение переноса тепла для области свободной влаги получено в виде:
дТ в_ д 2 Т в 2дТ в
2 dt дг2 г дг'
где к 2
__ Р в ^ в
: Лв .
С начальным условием:
V R вн < Г < R внеш (t), t — 0 ^Т в — Т(0) и двумя граничными условиями:
V г R:hJ > 0 ^ / , : д^;
V г — R внеш( t ) ,t > 0 ^
дь Яв dr ,
Л в Р в^Р — « са СТ в —
тЫ + Яв^. (8)
где Рп - давление пара при температуре поверхности, Па; Rcа - универсальная газовая постоянная, Дж/моль-K.
Уравнение (10) приведено к виду:
Rвнеш дt где к5 — ^.
5 P w
—к5(Сп — Сса ). (12)
С начальным условием:
V Г — Rвнеш(t),t — 0^Rвнеш(t) — R(0), где R(0) - начальное значение внешнего радиуса.
Введем безразмерную величину:
г
f R вн ■
Тогда математическая постановка задачи моделирования в период постоянной скорости сушки примет вид:
V 0 < f < ^н. t > 0 ^
где к'
дТ ев_ д2Т ев 2дТ ев
1 dt df 2 + r df, _ й2 (0)(£Р в С в + (1-£)Р т С т )
1 —
Л ев
.
Начальные и граничные условия уравнения (14):
V 0
V f— 0,(>0 ^ -Лев^в— 0
V f — fвн,t>0 ^ Тев — Тв
V fвн к' дТв = 2 dt где к' 2 — д2(°)РвСв Лв Начальные и уравнения (15) являются: д2Тв 2дТв aF+f "dr граничные условия V fвн
V f — fвн,t>0 ^ -Лев^ — -Лвд|
V f — fвнеш(t),t > 0 ^
_ . дТв
- Теа) + к 4 ^,
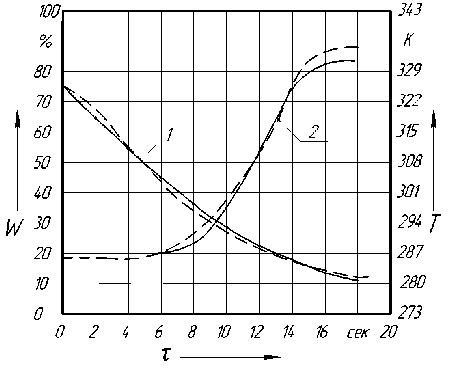
д^внеш ьв д^— к 3(Тв где к'з—^; к' 4 — ^(0)рв Лв Я2(0)Рв. V f — fвнеш(t),t>0 ^ д^'внеш dt где к'5 — . 5 Я(0)Рв -к‘5(Сп —Сеа), Начальное условие уравнения (17): v f — fвнеш(t), t — 0 ^ fвнеш(t) — 1 Для расчета коэффициентов конвективного тепло- и массообмена используется эмпирическая корреляция с коэффициентом 0,65 [7]. Nu — 2 + 0,65Re0-5Pr033; (18) Sh — 2 + 0,65Re0.55c0.33, (19) где Re — ^^а; Pr — ^^ Sc — ^-; Sh — —; Nu — ^y/—, Ц.а - скорость сушильного Dn Леа агента, м/с; ^еа - кинематическая вязкость, м2/с; сеа - удельная теплоемкость, Дж/кг-K; реа - плотность сушильного агента, кг/м3; с1н - наружный диаметр капли, м; Dn - диффузия водяного пара в воздухе, м2/с. В уравнениях, индексы са, н и п представляют сушильный агент, частицу и водяной пар, соответственно. Период постоянной скорости сушки заканчивается, когда вся свободная влага с поверхности капли будет удалена т.е. Rвнеш достигает Rвн (рисунок 1). Период убывающей скорости сушки. В период убывающей скорости сушки, предполагается существование углубления фронта испарения влаги, который делит каплю на область связанной влаги и область твердых частиц (рисунок 2). Рисунок 2. Капля в период убывающей скорости сушки Задача моделирования решалась при следующих упрощающих допущениях: 1. Тепло передается конвективно к поверхности капли. 2. Удаление влаги в порах капли описывается уменьшением радиуса области связанной влаги. 3. Радиус капли Rвн не меняется во время сушки. 4. Растворением твердых веществ в воде пренебрегаем. 5. Поры области связанной влаги заполнены воздухом, водяной пар диффундирует через эти поры. 6. Физические и транспортные свойства водяного пара рассчитываются при средней температуре, определенной как среднее арифметическое от температуры поверхности области связанной влаги и температуры поверхности капли. 7. Закон диффузии Фика с эффективным коэффициентом диффузии описывает диффузию паров воды через поры области связанной влаги. 8. Морфология капли не изменяется во время сушки. Принимая элемент дифференциального объема в области твердых веществ и учитывая тепловой баланс, получим уравнение переноса теплоты в виде: V 0 < r < s(t), t > 0 ^ д dt [^рв^вТсв + (1 ^)рт^тТсв] = -А^^Рсв), г2 дг m дТ . 1 д / 2дТво\ ! m2 дt г2 дг V дг ♦^(г^). г2дг дг где те же индексы и обозначения используются для моделирования периода постоянной скорости сушки, также используется для модельных уравнений, выведенных для период убывающей скорости сушки. Как и при получении уравнения (4) , после преобразования уравнения (20) получим окончательный вид уравнения теплопередачи для области связанной влаги: где m2 = (1 £)рт^т --------; тз Лво РвоМвСп Лво ■ _ = д2Тво 2 дСп дТво дt дг2 г m3 дг / дt дТво + (2тз + аС„ + тз г дг д2 Сп дг2 ■V ] 1 во ■ где т 1 = дТсв д2Тсв 2дТсв св св св m1 дt дг2 г дг ' £РвСв + (1-£)РтС. Лев ■ т , - начальное условие: V 0 < г< s(t), t = 0 ^ Тсв = T(t), - граничные условия: v г = 0, t > о ^ -л^д^ 0, V г = s(t), t > 0 ^ Тсв = Тз0, где индекс во представляет собой высушенную область и T(t) это температура капель в конце периода постоянной скорости. Уравнение теплопереноса высушенной части капли теплового балансов основано на элементе дифференциальной объема, занятого в области связанной влаги: V s(t) < г < Rbh, t > 0 ^ д г , с начальным условием: V s(t)<г<Двн,t = 0^Tво = Tт и с граничными условиями: V г = s(t), t > 0 ^ ds дтво ЗТсв ^Рв^в dt = лво дг+ лсв дг (29) V г - Rbh, t > 0 ^ -ЛводТ° = аса(Тво-Тса) (30) — [(1 - £)РтСтТк]= Л_1_д^2Т г2 дг (г ^к) г2 дг (г ТвоСп7во), где: 9во = -ЛводТв°; (23) и: Уво = -5воМвд^п. (24) Вво - эффективный коэффициент диффузии влаги в порах сухой части капли, м2/с. Уравнение (29) отражает тепловой баланс на границе испарения, в котором разница между теплом, передаваемом высушенной частью к поверхности капли используется для испарения некоторой части влаги из пор в области связанной влаги. Дальнейшее упрощение уравнения (29): £вЙ = -т4дТ£ + т5дТв, дt дгдг ЛЛ где т = —; т^ = 4£Рв 5£Рв Для того чтобы решить уравнение (28) и получить профиль концентрации водяного пара в порах области связанной влаги составляем материальный баланс по влаге для элемента дифференциального объема в области связанной влаги: V s(t) < г < Rbh, t > 0 ^ После получаем: ^[£МвСп]= -:1^д(г2]во) дt г2дг преобразования уравнения 5во = 3-£ дСп_д2Сп 2дСп т6 дt дг2 + г дг , Лво = ^Лсм + (1- £)Лт , (26) где Лсм - теплопроводность смеси паров воз-дух-вода существующих в порах высушенной части, Вт/ м-K. После преобразования уравнения и приведения подобных членов получаем окончательную форму уравнения теплопередачи: £ где т6 = —. ^во . Начальные и граничные условия, необходимые для решения уравнения (33): V 4(r) V г = s(t), t > 0 ^ Сп= ^^ п ЯсаТво V г = Rbh, t > 0 ^ -^вод^п = ^см(Сп - Сса) Баланс массы на поверхности испарения определяется уравнением: V г = (t), t > 0 ^ЕРв д| = DkMb д^п (34) Преобразование уравнения (34) представлено в виде: Я2 е где m 6 = -z-• -во Начальными и граничными условиями уравнения (44) являются: V s(t) < f < 1,t = 0 ^ Сп = рП(Т(^ П ЯсаТ(t) ds дСв эТ^д? D М„ где m7 =----. 7 ерв • Начальное условие, необходимое для решения уравнения (35): V f = s'(t),t>0 ^ Сп = ^ ^са^во V f =1,t>0^ —Dlод|п= RlHв(Cп V f = s'(t),t>oд^‘ = m'7д|1, — Сса) V г = s(t), t = 0 ^ s(t) = йвн Окончательный вид уравнений дели (21)-(36): V 0 < f < s'(t), t > 0 ^ мо- -Тсв -2Тсв 2 -Тсв m 1 dt = df 2 г df ’ где s'(t) безразмерный радиус связанной влаги. области m' 1 = ^вн(ЕрвСв + (1 Е^РтСт) Лев Начальные и граничные условия уравнения (37) являются: V 0 < f < s'(t),t = 0 ^ Тсв = T(t) v f = 0, t>0 ^ —Лев —Тв = 0 V f = s(t),t(0) ^ Тев = Тво V s'(t) < f < 1, t > 0 ^ D M„ где m 7 = 2-- ^внерв Начальное условие уравнения является: V f = s‘(t), t = 0 s'(t) = 1 Те же соотношения задаются уравнениями (40) и (41) и используются для расчета коэффициентов конвективного тепло- массопе-реноса в период убывающей скорости сушки. Модель (1)-(44) решена методом конечных разностей [8] с погрешностью результатов моделирования 12 % (рисунок 3). Проведена идентификация параметров модели по экспериментальным данным, полученным на опытной распылительной сушильной установке [3]. m дТо^д^+^ + дСп дТ,+ m2 д( дг2 г т3 дг д( +/2m3+dC, +m \ г дг д2С дг2 во , где: m' 2 = ^вн((1 Е)ртСт) Яво ; и: 1 - кривые сушки ПЗК, 2 - кривые нагрева; т'з = DвоMвCп Яво ■ Начальные и граничные условия уравнения (28) являются: V s'(t) < f < 1, t = 0 ^ Тво = T(t) V f = s'(t), t > 0 ^ - модель; - - эксперемент. Рисунок 3. Сравнение расчесчетных и экспериментальных кривых сушки ПЗК и кривых нагрева при Тса = 373K, Wн.пзк= 75% -v вdt V f = 1, t > 0 ^ ■ m^^f + m's^ 4df 5df ^^^^^в Лво-^Г = Явна(Тво — Тса), Л Л где m 4 ~~ m5 т— V s'(t) < f < 1, t > 0 ^ д^п д2£п 2 д^п m 6 St = df2 + f df’ Таким образом, уравнения (1)-(44) являются математической моделью, решение которой позволяет определять изменение влажности (концентрации СВ) и температуры по радиусу капли в процессе распылительной сушки концентрата ПЗК, что необходимо как для выбора геометрических размеров сушилки, так и для управления технологическими параметрами сушки.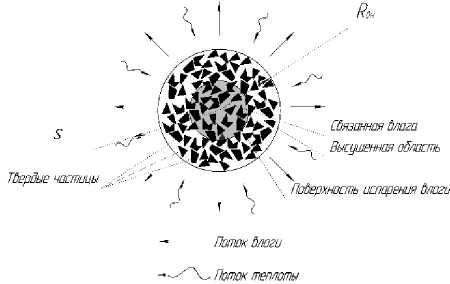
Список литературы Моделирование процесса распылительной сушки суспензии протеинового зеленого концентрата (ПЗК)
- Дерканосова А.А., Коротаева А.А. Перспективы использования протеинового зеленого концентрата (ПЗК) в кормопроизводстве//«Наука и технологии в современном обществе» материалы международной научно-практической конференции: в 2 частях. Уфа, 2014. С. 142-143.
- Шевцов А.А., Дранников А.В., Коротаева А.А., Дерканосова А.А. Анализ инновационной привлекательности использования вегетативной массы растений в комбикормах//Вестник Воронежского государственного университета инженерных технологий. 2013. № 1. С. 224-226.
- Магомедов Г.О., Магомедов М.Г., Шахов С.В., Саранов И.А. и др. Установка для агломерирования пищевых порошкообразных полуфабрикатов комбинированным способом//Современные наукоемкие технологии. 2014. № 6. С. 69-70.
- Гордиенко М.Г. Моделирование и разработка непрерывной технологии распылительной сушки пробиотиков: на примере сушки биосуспензии бифидобактерий: дис. … канд. тех. наук: 05.17.08: защищена 05.02.06: утв. 10.06.71. М.: РХТУ, 2006. 200 с.
- Куцов С.В., Дранников А.В. Физико-математическое моделирование процесса обжарки зерна овса//Вестник Воронежского государственного университета инженерных технологий. 2008. № 1. С. 26-30.
- Волькенштейн В.С. Скоростной метод определения теплофизических характеристик материалов. Л.: Энергия, 1971.
- Ranz W. E., Marshall W. R. Evaporation from drops//Chem. Eng. Prog. 1952. Т. 48. №. 3. С. 141-146.
- Тихонов А. Н., Самарский А. А. Уравнения математической физики. М.: Изд-во МГУ, 1999. 798 с.


