Моделирование процесса роста тонких пленок

Ключевые     слова:      компьютерное     моделирование, термодинамический метод, метод молекулярной динамики, методы клеточных автоматов, энтропия.

В современной технологии широко используются различные методы для осаждения тонких пленок, но все они являются косвенными [1]. Следовательно, требуется некоторая модель физико-химических процессов, происходящих в установке и образце, используя которую возможно было бы расшифровать результаты измерений, составить представление о структуре выращиваемой пленки и о кинетике преобразований рельефа в процессе роста.

В настоящее время на основе трех таких моделей существуют следующие методы:

• 1.   Термодинамические методы;

• 2.   Методы молекулярной динамики;

• 3.   Методы клеточных автоматов.

Термодинамические методы используют в качестве своей теоретической базы аппарат равновесной и неравновесной термодинамики и статистической физики. Процессы и объекты описываются в рамках макроскопических переменных, абстрагируясь при этом от микроскопической структуры материальных сред.

Эволюция моделируемой системы во времени имеет детерминированный характер, подчиняясь строгим уравнениям состояния системы. Статистические флуктуации макроскопических параметров имеют весьма малую величину (ввиду большого количества микрочастиц в системе) и поэтому пренебрегается их негативным влиянием на состояние системы.

Основная трудность при использовании этого метода состоит в необходимости предварительной разработки уравнений состояния системы. В этой связи большинство уравнений состояния, учитывающих специфику объекта, определяется с помощью привлечения эмпирических методов.

Метод молекулярной динамики ‒ эффективный численный метод анализа материальных сред, для которых справедливо представление о длине свободного пробега микрочастиц. Метод основан на прямом численном интегрировании механических уравнений движения микрочастиц и дальнейшей обработки их фазовых траекторий с целью получения интегральных (термодинамических) характеристик системы [2].

Использование данного метода затруднено и мало эффективно при рассмотрении материальных сред в конденсированном состоянии. Метод применяется в основном для анализа систем с малым количеством микрочастиц (ввиду чрезвычайно высоких требований, предъявляемых к быстродействию и объему оперативной памяти вычислительных средств, при повышении количества анализируемых микрочастиц).

Методы клеточных автоматов основаны на представлении моделируемой системы в виде пространственно-распределенной совокупности индивидуальных взаимосвязанных ячеек, состояние которых претерпевают изменения синхронным образом через дискретные интервалы времени, и в соответствии с определенными локальными правилами эволюции системы [3].

В таблице 1 представлены результаты сравнительного анализа эффективности различных методов численного моделирования.

Таблица 1 ‒ Сравнительный анализ эффективности различных методов моделирования

Критерий сравнения	Термодинамический метод	Метод молекулярной динамики	Метод клеточного автомата
Возможность анализа микро- и наносистем	Нет	Да	Да
Возможность учета флуктуаций параметров	Ограничена	Нет	Да
Возможность комплексного анализа процессов	Ограничена	Нет	Да
Универсальность метода моделирования	Ограничена	Нет	Да
Наглядность отображения результатов моделирования	Да	Ограничена	Да

Исходя из анализа данных таблицы 1, можно сделать вывод о предпочтительности использования моделирования методами клеточных автоматов. Однако, как правило, на практике невозможно руководствоваться микропараметрами системы, но можно относительно точно определить макропараметры, такие как давление и температура в камере, скорость осаждения частиц и т.п. Размер получаемых пленок также влияет на выбор метода моделирования. Так, например, для метода клеточных автоматов с увеличением площади подложки экспоненциально возрастает количество вычислений, тем самым увеличивается либо время моделирования, либо требуемая мощность ЭВМ. В свою очередь для двух других методов такая зависимость не прослеживается. Таким образом, на основе всего выше сказанного для практического применения наиболее рациональным будет сделать выбор в пользу термодинамического метода моделирования (ТДМ).

Расчет термодинамического равновесия произвольных систем осуществляется путем минимизации изобарно-изотермического потенциала или максимизации энтропии системы при учете всех потенциально возможных в равновесии индивидуальных веществ q. Расчетные методы развиты на основе вариационных принципов термодинамики [4]:

• 1.    Из всех допустимых значений молей М q индивидуальных веществ в термодинамической системе те из них, которые минимизируют термодинамический потенциал системы, соответствуют равновесным значениям;

• 2.    Из всех допустимых значений энергии U i , вносимой каждым независимым компонентом (атомом), те из них, которые максимизируют суммарный вклад энергии отдельных атомов в систему, соответствуют равновесным значениям.

Экстенсивными термодинамическими параметрами системы, т.е. пропорциональными количеству или массе вещества в системе, являются объем V, энтропия S, внутренняя энергия U, энтальпия H, энергия Гельмгольца F (F = U - T·S), энергия Гиббса G (G = H - T·S); интенсивными термодинамическими параметрами, т.е. не зависящими от количества или массы системы, являются давление P, термодинамическая температура T, концентрация, мольные и удельные термодинамические величины.

Для того, чтобы представить в явном виде любую термодинамическую систему следует задать два независимых параметра из числа V, S, U, H, P, T, F, G и полный исходный химический состав системы.

Критерием достижения системой равновесного состояния является экстремум ее характеристической функции. При независимых параметрах P и Т характеристической функцией является свободная энергия Гиббса G, а минимум этой энергии системы (G min ) является критерием достижения равновесного состояния; при параметрах U и V для изолированной системы характеристической функцией является энтропия S, а максимум энтропии системы S max является критерием достижения равновесного состояния [5].

Экспериментальное измерение термодинамических функций (теплоемкости, внутренней энергии и т. д.) очень сложная задача. Поэтому информацию о термодинамических функциях газов в стандартном состоянии обычно получают расчетным путем [6].

Термодинамические функции вещества в состоянии идеального газа могут быть вычислены через статистическую сумму по состояниям молекул (атомов) газа:

Q(T) = v,,exp—-, где si - энергия i-го состояния молекулы (атома), s0 — энергия ее нижнего (основного) состояния, pi - статистический вес i-го состояния, k -постоянная Больцмана. Суммирование проводится по всем состояниям (i). Термодинамические функции одного моля газа, состоящего из тождественных молекул и находящегося в стандартном состоянии, связаны со значениями статистической суммы и ее производных следующими соотношениями:

5°(T) = R ln — + RT 8lnQ(T), v у          N            d T ’

H° (T) = H° (0) + RT2 -^y-. д T

Ф°(T) = Rln^, NA

Cp°(T) = RT2 ' lnQ(T) + 2RT 9lnQ(J), д T2               d T

U°(T) = H° (T) - RT.

Ф ° (Т) - приведенная энергия Гиббса:

Ф (T) = 5 (T) -

H ° (T)—H ° (0)

t      , где H°(0) - энтальпия вещества при 0 K, NA - число Авогадро, R -газовая постоянная. Символ ° - означает, что значение свойства относится к стандартному состоянию.

Термодинамические функции веществ в конденсированном состоянии можно рассчитать при помощи соотношений:

с °     _ V fTk+1 ^P(T) Jm .  ^71—1 AtrH (Tk+1)

5 (T) = LkjTk  — ^7 + Lk=0 Tk+1  ,

H ° (T)= &_fH* (0) + 2 k j Ty * c ; (T)dT+ Hi—, ¹ A _trH ° (T k ₊ i ), где T k+i и A _trH ° (T k+i ) - температура и изменение энтальпии для фазового или полиморфного превращения. Зависимость теплоемкости конденсированного вещества определяется, как правило, экспериментально [7].

Для термодинамических расчетов процессов с возможностью протекания химических реакций используется так называемая полная энтальпия вещества:

Н°(Т = ^fHo(T0) + [H0(D - НЧТК где

[Н°(Т) — H°(To)] = J^c;(T)dT,

∆ f H°(T 0 ) - стандартная энтальпия образования вещества при температуре T 0 .

Следует помнить, что значение энтальпии вещества зависит от того, какая температура (0 или 298.15 К) выбрана в качестве уровня отсчета.

Использование понятий полной внутренней энергии и энтальпии существенно облегчает решение задачи расчета равновесного состава многокомпонентных химически реагирующих систем, поскольку задает уровень отсчета энергии.

В ходе термодинамического моделирования определение свойств производится при помощи аппроксимации выражения вида [8]:

Ф = - -—^ = /1 + f2\nx+ ^ + - + f5x+ f6x2 + f7X3.

Однако в справочной литературе информация о величинах f 1 – f 7 отсутствует, но приводятся величины коэффициентов ряда, описывающего изобарическую теплоемкость согласно выражению:

Ср = а + Ь Т + с Т2 + ^^ + d Т3.

Поэтому объективная потребность в создании баз данных для новых веществ требует осуществления перевода коэффициентов а, b, с, с' и d в коэффициенты f 1 – f 7 . Данное преобразование может быть выполнено следующим образом:

S = - ^^-;G = Н^-ФТ = Н0- 104Фх;x = -^-.

dT           ^{0              0}                     10⁴

Тогда s =

- — 104 - ф + %^- ф + % dx              dx

(2- Хз— Tx+fs+2 f %+

3 f y %²) = =

f1 + f2 ln% + - + - + f5% + f6%2 + f7%3 + f2 - - -

^ + f5 % + + 2 f6 %2 + 3 /7 %3-(fi+f2) + f2ln% + A + 2 f % +

3 f6 %2 + 4 f7 %3 .

Выражение для энтальпии примет следующий вид:

H = G - T S = //0 + Ф T-T S = H0 + 104 % (Ф - S) = H0 +

+ 104 (- f2 %+ |3+ I4- fs %2- 2 f6 %2- 3 f7 %4) .

Следовательно

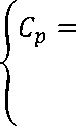
^T-    104 - -f2-%2-2 fs %-4 f6 %2-12 f7 %3

д           R 9    10-8 с'    1012

Cp - a + 104 b % + 108 с %2 +--—--+ —^

Таким образом, рассмотренный в данной работе метод термодинамического моделирования позволяет моделировать реальные системы при любых параметрах состояния. Результатом такого моделирования может являться определение равновесного состава, расчет выхода целевого продукта, определение неизвестных термодинамических параметров процессов, вычисление свойств различных сред и многое другое.