Моделирование процесса шумообразования фрезерных деревообрабатывающих станков с опорами двойного действия с газовой смазкой

Введение. Деревообрабатывающие станки интенсивно эксплуатируются в различных отраслях промышленности, включая предприятия транспортного машиностроения. Корпусные и базовые детали являются основными источниками акустического излучения в интервале частот 31,5-500 Гц. По данным работы [1], у токарно-винторезных станков доля звуковой мощности шпиндельных бабок в общем звуковом поле станка составляет 48-52%, а станины – 33-35%. Следует иметь в виду, что основным источником возбуждения колебаний станины является именно шпиндельная бабка. Аналогичная картина, согласно исследованиям [2-4], наблюдается у токарноревольверного станка 1325ФЗО: для шпиндельной бабки составляет 48-50%, а станины – 42-45%; у токарно-револьверных станков 1Д325 и 1Е316П вклад источников более равномерный: шпиндельная бабка 32-35%, коробка подач 30-32%.

Корпусные детали принадлежат к классу энергетически замкнутых конструкций с небольшим коэффициентом потерь. Задача расчёта излучения звука такими конструкциями сводится к определению амплитуд колебательных скоростей соответствующих стенок, которые находятся из уравнений энергетического баланса. Ввод вибромощности в корпуса таких узлов, как шпиндельная бабка, редуктор, коробка подач, осуществляется только через подшипниковые опоры. Тогда система уравнений энергетического баланса может быть записана в виде [5] K 1                                     K 1                                 k 2

У(5, S, + a ,l,     ² = У«, У ZV, ² + 2п R_hTN , Z =-пп, fM. ,          (1)

i i                   H              i* i                  il^ i i

где 5 I - коэффициенты поглощения энергии в стенках корпуса, м^-1; a _{i-J; J—i} - коэффициенты передачи между двумя соседними стенками корпуса; l i–j – длина линии контакта между двумя пластинами, м; R Hi – радиус наружного кольца подшипника, м; К 1 – количество стенок корпуса; К 2 – количество подшипников в соответствующей стенке; V i – виброскорости стенок, м/с; z i – эффективный коэффициент потерь колебательной энергии в стенках корпуса; f i – собственные частоты колебаний, Гц; M i – масса стенки, кг.

Коэффициенты затухания для чугунного корпуса определяются по формуле

5 i = 0,03п

Г f

0,5

к

hj

Коэффициент прохождения энергии изгибной волны из пластины в пластину определяется по формуле

a

i ^- j

= 2

2,5

( h; )

1 +

2,5

(tJ

- 2

V

, n

где v — функция, учитывающая соотношение толщин пластин.

Вибромощность энергетического потока, вводимого через опору качения в корпус в соответствующей полосе частот, вычисляется по зависимости

N i = x <  PV > .                                 (4)

Здесь P и V – сила и скорость деформации в местах контакта шариков (роликов) с дорожкой качения наружного кольца (угловые скобки обозначают усреднение по времени); х - коэффициент мощности в соответствующей полосе частот, зависящий от формы импульса силы.

На основе рассчитанных виброскоростей стенок корпуса определяются уровни звукового давления с использованием известного интеграла Релея-Гюйгенса. Расчёт виброскоростей стенок корпуса для шпиндельных бабок токарно-револьверных и токарно-винторезных станков принципиальных отличий не имеет, хотя их компоновки с позиций ввода в корпус вибромощности имеют существенные различия. У высокоскоростных токарно-револьверных станков мод. 1Е316П, 1Д325, 1325ФЗО шпиндельные бабки представляют собой прямоугольный параллелепипед без промежуточных стенок, без промежуточных валов и приводных зубчатых колёс, поэтому система (1) состоит из шести уравнений. Привод шпинделя осуществляется клиноременной передачей. Вибромощность в корпус переносится через переднюю и заднюю опоры шпинделя. Вводимая в корпус вибромощность определяется через деформации опор с учётом нагрузок только от процесса резания.

Шпиндельные бабки токарно-винторезных станков также представляют собой конструкцию, близкую по форме к прямоугольному параллелепипеду, но с несколькими промежуточными стенками, несколькими подшипниками в каждой стенке и большим количеством зубчатых передач. Именно этими обстоятельствами определяется подход к расчёту вибромощности, передаваемой через шпиндельные опоры. Для опор шпинделя сила и скорость деформации в подшипниках определяется с учётом нагрузок от процесса резания и зубчатых передач, а для промежуточных опор учитываются реакции от действия сил в зубчатых зацеплениях.

Из системы уравнений энергетического баланса определяются виброскорости на собственных формах колебаний стенок и уровни шума. Как видно из полученных зависимостей, снижение вибраций может быть достигнуто уменьшением вводимой в корпус вибромощности от подшипниковых узлов. Поэтому не только теоретический, но и практический интерес представляет замена подшипников качения в опорах шпинделей на подшипники скольжения различных конструкций.

Действительно, подшипники скольжения обладают не только повышенными демпфирующими характеристиками, но и имеют значительную площадь опорной поверхности. Эти их особенности позволяют предположить, что вводимая в корпус шпиндельных бабок вибрационная мощность существенно понизится. Однако следует отметить, что замена подшипников качения на подшипники скольжения возможна только при условии сохранения нагрузочных и точностных характеристик. Ниже приводится расчёт нагрузочных характеристик упорного газодинамического подшипника, обладающего по несущей способности свойством подшипника двойного действия .

Термин «подшипник двойного действия» использован в работе [6]. В ней вводится следующее понятие: если подшипники, в которых несущая способность развивается только за счёт увеличения давления с одной стороны нагруженного элемента, определить как подшипники простого действия , то можно использовать термин «подшипники двойного действия» в тех случаях, когда несущая способность является результатом как возрастания давления с одной стороны, так и уменьшения давления с другой стороны нагруженного элемента. Приведённый в работе [6] подшипник двойного действия состоит из направляющей, которая движется относительно неподвижного элемента так, что движение происходит в направлении сужения зазора. При этом аналогичный неподвижный элемент (ползун) расположен по другую сторону поверхности движения. В результате движение происходит в направлении расширения зазора относительно этого элемен- 12

та, т. е. подшипник становится подшипником двойного действия. Несущая способность подшипника двойного действия есть сумма несущей способности, получаемой в основной части подшипника простого действия, и дополнительной несущей способности, получаемой в части подшипника с расширяющимся зазором. Потенциальные возможности подшипника двойного действия в работе [6] приведены для подшипника бесконечной длины, для которой уравнение Рейнольдса легко решается. Для подшипника конечной длины анализ работы подшипника двойного действия приведён в работе [7].

Расчет упорного газодинамического подшипника двойного действия. Основная цель данной работы – привести потенциальные возможности подшипника двойного действия в случае, когда элементы (ползуны), расположенные по обе стороны от направляющей, совершают колебания в направлении, перпендикулярном плоскости направляющей (рисунок). Кроме того, в качестве исходных уравнений возьмём уравнения движения вязкого газа с учётом сил инерций [8, 9]:

d² u dp d u f Su du)

ц —2- = — + p— + p u — + u—I, d y ² dx d t ( d x dy )

Ip = 0, ^^( P ^u ) ⁺ ^( P ^u ) = 0, P = P RT ^. оy      dt оx      оy

Здесь ц - динамический коэффициент вязкости; u , u - компоненты вектора скорости; р - гидродинамическое давление; р - плотность; R - газовая постоянная; Т - температура.

Уравнения подвижных элементов (совершающих колебания) будем искать в виде:

y = h ( x , t ) = h m + xtga + Ф ( t ); y = H ( x , t ) = h _M - xtga - Ф ( t ).

Рассмотрим нестационарное движение газовой смазки между двумя пластинами (между ползуном и направляющей). Одна из пластин (направляющая), уравнение которой y = 0, считается бесконечной и движется с постоянной скоростью u ₀ в отрицательном направлении оси Ох (см. рисунок).

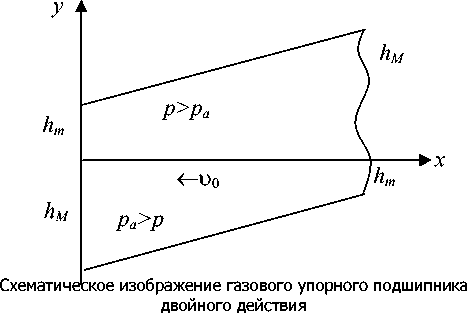
Другая пластина (ползун), уравнение которой y = h + xtg a + Ф ( t ) = h ( x , t ) , считается полу-бесконечной ( х > 0 ), образует с первой угол a и движется (колеблется со скоростью Ф( t ) ) в направлении, перпендикулярном бесконечной пластине.

Система уравнений (5) сначала решается при следующих начальных и граничных условиях:

u = -u₀, u = 0 при y = 0; u = 0; u = Ф '( t ) при y = h ( x, t ).                        (6)

Так как поверхность ползуна совершает колебания в направлении, перпендикулярном оси Ох, то в сечении х = 0 возникают флуктуации граничного условия для гидродинамического давления. Следовательно, в качестве дополнительного граничного условия для газодинамического давления будем иметь:

Р = P a h m / ( h m + Ф ( t ) ) ,                                   (7)

где Ф( t ) характеризует заданную степень гармонического колебания.

Введём функцию у( x , У , t ), аналогичную функции тока:

ду ри = —; ри = ду

ду д p --у — .

д x     д t

Точное автомодельное решение задачи (5)-(6) будем искать в виде [9]: у( x , у , t ) = у(С); p = p a h m ; С =       .

h ( x , t )         h ( x , t )

Подставляя (9) в (5) и (6), будем иметь:

d 3y    c2         у'RT v—y = -—tga; u =----;

d С     RT         c

у'-С tg a- RT и =       ------+ С Ф'(t);

c

у'(С) =-и⁰ при c = 0; у'(С) = 0 при c = 1, c ² = p ² h²_m.

Решение задачи (10)-(11) легко находится непосредственным интегрированием. В результате будем иметь:

c2       c2    c2       С цу (c) = -—tg a-—+—tg a•- + цuоc-цuо;

RT     2 RT     2

p =

p h pa m .

h ₀ + xtg a + Ф ( t )

C учётом (12) для несущей способности подшипника, вносимой сужающимся зазором, получаем следующее выражение нагрузки, приходящейся на единицу длины подшипника:

r     ph       ph      ph

[ -----p a m--- p a m   dx = p am

0 L hm + xtga + Ф(t)  hm + Ф(t) J     tga k-1 - Фй

In — k^h

1 + ФЙ  1 + Фй hm         hm

где k = h _m I h _m ; l - единица длины.

В случае, когда поверхность подшипника совершает гармонические колебания в направлении, перпендикулярном плоскости направляющей, т.е. когда Ф( t ) = A sino t , будем иметь:

P =

p _a h _m

h _m + xtg a + A sin ю t

p _a h _m

^; w c =---- tg a

In—

1 +

k

-

k -1

-

A sin ю t h _m

A sin ю t    ,  A sin ю t

--------    1 +--------

.

h _m

h _m

В случае подшипника с расширяющимся зазором решение задачи (5)-(7) также ищется в виде (9), полагая здесь С= y/H(x,t).

Для подшипника простого действия p =

р h pa m

h _m + xtg a + Ф ( t )

и несущая способность осредня-

ется формулой (14).

Для подшипника двойного действия нагрузка, вносимая расширяющимся зазором единичной длины, определяется выражением:

l wP =f

0 _

pahM           pahM hM - Ф (t)  hM - xtga- Ф (t)

dx = p a h m. tg a

k - 1

-

Ф ( t ) h_m

k - Ф^^? 1 h_m

+ In

1 k^^M h_m

.

В случае, когда Ф(t) = Asinot, wp

p = Т" h_M

p_al " ^k

k - 1 - ? < t > h_m

р h pa m

;

- xtg a- A sin ю t

k - 1

-

A sin ю t h_m

, A sin ю t k-- h_m

+ In

, A sin ю t k-- h_m

.

В результате определяется w – несущая способность подшипника как сумма несущей способности w c , полученной в основной части подшипника простого действия, и дополнительной несущей способности w_p , получаемой в части подшипника с расширяющимся зазором:

w = W c + W p , (17)

где w c и w_p соответственно определяются выражениями (14) и (15).

Деля уравнение (14) на уравнение (16) при Ф( t ) = 0 , получаем отношение составляющих нагрузки от двух частей подшипника:

w п = — wp

к - 1 - Ink к Ink - к + 1

Из (18) следует, что максимальное значение п приближается к 1 при к ^1 . Это означает, что подшипник двойного действия эффективен при низких нагрузках.

Из полученных аналитических выражений (14) и (16) следует:

• 1.    При Ф( t ) = 0, к ^ 1, w c = 0, w_p = 0, w = 0. Следовательно, несущая способность подшипника равна нулю.

• 2.    При Ф( t ) ф 0, к ^ 1, w c ф 0, w_p ф 0, w ф 0 подшипник обладает несущей способностью, обусловленной колеблющимися поверхностями элементов (ползунов) подшипника двойного действия.

• 3.    Полученные здесь зависимости используются при решении системы уравнений энергетического баланса и позволяют на этапе проектирования выполнить реальный расчёт виброаку-стических характеристик шпиндельных бабок.

Заключение. Для снижения вибрационной мощности, вводимой в корпус шпиндельных бабок предлагается заменить подшипники качения в опорах шпинделей на подшипники скольжения. Даётся расчёт упорного газодинамического подшипника двойного действия.