Моделирование процесса швартовки к борту судна-партнера на финальном этапе сближения судов "борт к борту" с использованием инновационного способа управления судном

Аварии с судами разных типов и тоннажа происходят практически ежедневно. Для повышения безопасности проведения швартовных операций был разработан способ управления судном при швартовке к борту судна-партнера ( Холичев и др ., 2015).

Наиболее опасным при проведении любой швартовной операции является заключительный (финальный) этап – контакт судна с причалом, плавбазой или другим судном. Автоматизация процесса швартовки судов повышает безопасность любого вида швартовки, т.к. позволяет избежать ошибок человеческого элемента. В статье представлен инновационный способ швартовки к борту судна-партнера и результаты модельного эксперимента, проведенного авторами с целью доказать возможность применения данного способа на практике.

2.    Способ швартовки к борту судна-партнера

На кафедре судовождения МГТУ разработан способ управления швартующимся судном при выполнении им швартовной операции к борту судна-партнера ( Юдин и др. , 2013a), когда в пределах контуров швартующегося судна и судна-партнера в их диаметральных плоскостях выбирают по две точки, одна из которых находится на носовой части А (швартующееся судно), А п (судно-партнер), другая – на кормовой части В (швартующееся судно), В_п (судно-партнер) относительно мидель-шпангоута соответствующего судна.

Координаты точек А , В , А_п , В_п в неподвижной координатной системе определяют непрерывно с высокой точностью (±1,0 м). Используя значения координат точек швартующегося судна А ( X 0 A , Y 0 A ), В ( X 0 B , Y 0 B ) и судна-партнера А п ( X 0 Aп , Y 0 Aп ), В п ( X 0 Вп , Y 0 Вп ) в неподвижной координатной системе, координаты тех же точек в подвижных системах координат, связанных c швартующимся судном А ( X A , Y A ), В ( X B , Y B ) и судном-партнером А п ( X Aп , Y Aп ), В п ( X Вп , Y Вп ), координаты центров тяжести (ЦТ) швартующегося судна в связанной с ним подвижной координатной системе G ( X_G , Y_G ) и судна-партнера в связанной с ним подвижной координатной системе G_п ( X _{0 Gп} , Y _{0 Gп} ), а также значения расстояния между диаметральными плоскостями (ДП) швартующихся судов h ₀ и расстояние между ЦТ швартующихся судов m рассчитывают ( Юдин и др. , 2013b):

• –    координаты центра тяжести швартующегося судна G ( X _{0 G} , Y _{0 G} ) в неподвижной координатной системе;

• –    координаты центра тяжести судна-партнера G п ( X 0 Gп , Y 0 Gп ) в неподвижной координатной системе;

• –    координаты точек А _п ( Х_{А п} , Y_Aп ) и В _п ( X_{B п} , Y_{B п} ), расположенных на перпендикулярах к ДП судна-партнера восстановленных в точки А_п и В_п (рис. 1);

• -    координаты проекции ЦТ судна-партнера G П ( X 0 G _П , Y ₀ G _П ) в неподвижной координатной системе на траекторию сближения в конечной стадии швартовки, проходящую параллельно ДП судна-партнера через точки A П и В П ;

• -    координаты второй заданной точки Р ₂( X 0 P ₂, Y ₀ P ₂) в неподвижной координатной системе;

• -    текущее значение длины тормозного пути S _т;

• -    координаты первой заданной точки Р ₁ ( X 0 P _b Y ₀ P ₁) в неподвижной координатной системе.

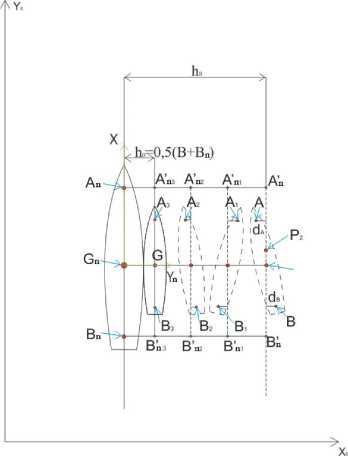
Рис. 1. Схема сближения швартующихся судов "борт к борту" в условиях открытого моря

Момент выхода швартующегося судна во вторую заданную точку Р ₂ соответствует равенству координат ЦТ швартующегося судна и второй заданной точки, т.е. X 0 G = X 0 P ₂, Y ₀ G = Y ₀ P ₂.

После выхода швартующегося судна в точку Р2 осуществляется дальнейшее сближение швартующихся судов до непосредственного контакта "борт к борту". С этой целью заданное текущее положение траектории сближения швартующихся судов, т.е. линия АПВП постепенно смещается параллельно ДП судна-партнера в сторону судна-партнера со скоростью не больше допустимого значения скорости поперечного движения швартующегося судна в направлении судна-партнера уд. Скорость ь>д определяется исходя из безопасности швартовной операции, а именно из условия безопасного гашения поперечной скорости движения швартующегося судна в момент непосредственного контакта швартующихся судов средствами кранцевой защиты борта судна-партнера. Параллельное смещение линии А ПВ П в сторону судна-партнера обусловлено смещением точек А П и В П, текущее положение которых рассчитывается непрерывно в зависимости от значения расстояния h между бортами швартующихся судов. Постепенное уменьшение значения h в соответствии с законом dh/dt = f( уд, h, hо, ...)

приводит к изменению значения задаваемого расчетным способом расстояния между ДП швартующихся судов h ₀ = h + 0,5 x ( В_П + В ) (здесь В_П - ширина судна-партнера, В - ширина швартующегося судна), что в свою очередь изменяет координаты точек А П и В П , и в конечном итоге линия А П В П смещается в сторону судна-партнера, оставаясь параллельной его ДП.

Смещение линии А П В П от исходного положения в сторону судна-партнера образует смещение d_А , d_В носовой А и кормовой В точек швартующегося судна соответственно. Формируется сигнал управления а = - k_Axd_A + k_Bxd_B , и ДП швартующегося судна приводится к новому положению линии А П В П до их полного совпадения. Далее процесс смещения линии А П В П по указанному алгоритму в сторону судна-партнера будет повторяться многократно, также многократно будут образовываться смещения носовой d_А и кормовой d_В точек швартующегося судна относительно текущего положения линии А П В П . Смещения носовой А и кормовой точек В швартующегося судна относительно текущего положения линии А П В П будет приводить к формированию управляющего сигнала средства управления швартующимся судном. Работа средства управления вернет ДП швартующегося судна на линию, совпадающую с текущим положением линии А П В П .

Смещение линии А _пВ _п в сторону судна-партнера будет происходить до тех пор, пока расстояние h ₀ между ДП швартующихся судов не будет равно значению, определяемому из выражения h ₀ = 0,5 ( В_п + В ), т.е. в этот момент расстояние между бортами швартующихся судов будет равно нулю h = 0. Указанный момент в предлагаемом способе управления судном при выполнении им швартовной операции к борту судна-партнера считается моментом окончания швартовной операции.

В результате применения данного изобретения достигается возможность получения технического результата – соблюдение условия завершения швартовной операции, т.е. осуществления непосредственного контакта ("борт к борту") швартующихся судов.

3.    Модельный эксперимент

Стратегией на данном этапе является управление танкером по отклонениям от некоторой прямой, названной прицельной линией – ПЛ. Это прямая, смещенная от точки нахождения цели в данный момент, которая имеет направление курса цели, т.е. направление ее ДП. Отклонения носовой и кормовой точек ДП танкера от прицельной линии определяются следующим образом:

dn = -( xs-x_z )xcos( K ) + ( ys-y_z )xsin( K_z ) + d 0 + p xsin( K_z kKs );

dk = -( xs-x_z )xcos( K ) + ( ys-y_z )xsin( K_z ) + d 0- p xsin( K_z kSCs ).

Мы используем их для формирования управляющего сигнала системы управления с помощью соотношения sign – a1 × dn  a2 × dk, при этом параметры выбраны так: а1 = 1.1 и а2 = 0.9. Выбор этих параметров равными по величине приводит к управлению по направлению (Пашенцев, Юдин, 2013). Далее мы проведем оптимизационный подбор а1 и а2.

Эти формулы дают возможность моделировать движение танкера на втором этапе подхода к месту швартовки. Напомним также, что для работы на этом этапе швартовой операции мы выбрали для судна математическую модель в перемещениях. Она была идентифицирована нами ранее и используется здесь как единственная для моделирования движения. Чтобы сделать управление по отклонениям близким к реальной ситуации, нам надо получить данные о траектории движения цели. Возьмем в качестве таковой судно, лежащее в дрейфе и перемещающееся под действием внешних факторов. Выберем для этого действие ветра. Проводим моделирование движения дрейфующего судна при скорости ветра 10 м/с c направления 60 , нос судна направлен на 10 , скорость хода 0.1 м/с. Эта скорость хода необходима формально из-за структуры модели в перемещениях. В ней много членов, где скорость входит в знаменатель, поэтому она не может быть нулевой. После того, как моделирование дрейфа выполнено, координаты и курс дрейфующего судна запоминаются в трех массивах. При моделировании работы системы управления по отклонениям эти запомненные данные используются как целевые для динамического построения прицельной линии.

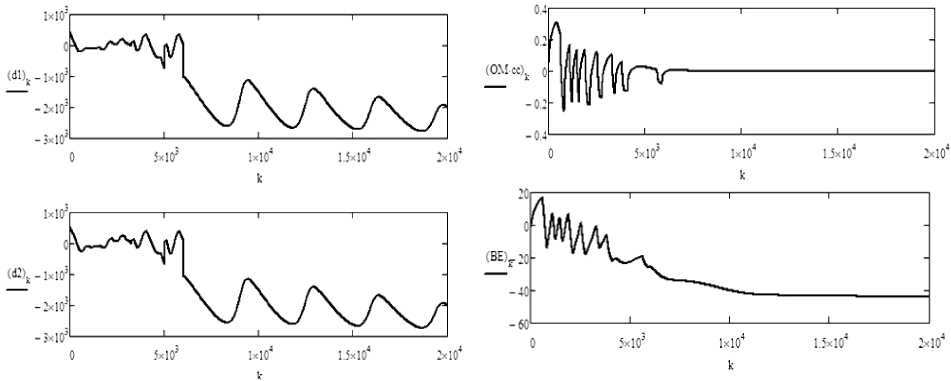
Рис. 2. Изменения во времени (сек) отклонений носовой и кормовой точек (м), угловой скорости поворота (°/с) и угла дрейфа (°) танкера при управлении по отклонениям

И только потом относительно этой линии идет управление по отклонениям. На рис. 2 и 3 приведены результаты движения швартующегося танкера при этом управлении.

На рис. 2 приведены изменения во времени отклонений носовой и кормовой точек танкера от прицельной линии, угловой скорости поворота и угла дрейфа танкера при управлении по отклонениям. Хорошо видно, что сильные изменения параметров имеют место в начальный период движения. Танкер производит разворот, во время которого происходят колебательные изменения параметров. Затем танкер ложится на устойчивый курс с небольшими изменениями кинематических параметров.

На рис. 3 приведены изменения во времени курса, управляющего сигнала, скорости перекладки руля и траектория танкера. Приведены две траектории – самого управляемого танкера (сплошная линии) и дрейфующего объекта швартовки (точечная линия). На траектории танкера хорошо виден начальный маневр с выходом на прицельную линию.

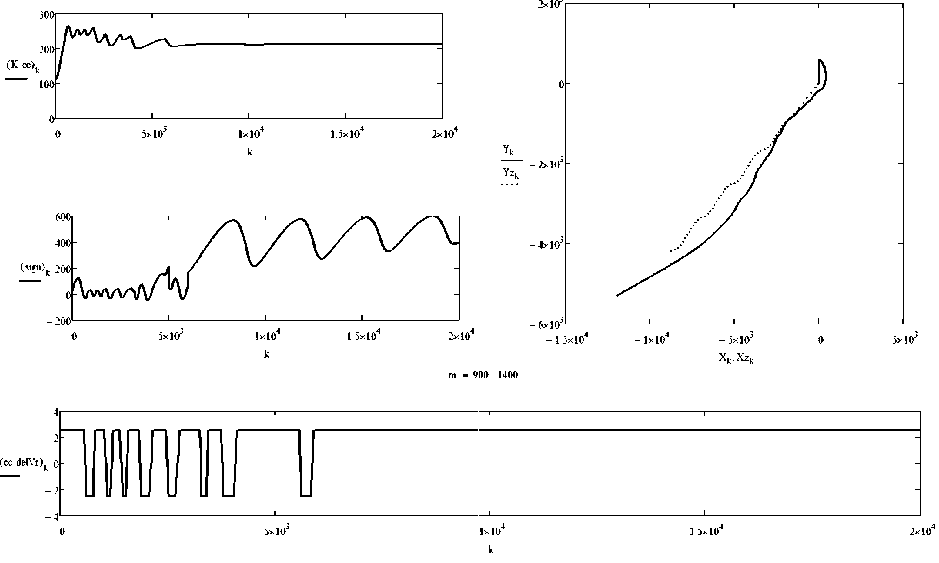
Рис. 3. Изменения во времени (сек) курса (°), управляющего сигнала, скорости перекладки руля (°/с) и траектория танкера при управлении по отклонениям

Однако на этих рисунках нет изображения самой прицельной линии. Это понятно, так как прицельная линия меняет ежесекундно свое положение. Это происходит в соответствие с перемещением цели и изменением ее курса. Но в программе моделирования в среде VB6 запрограммирована возможность проследить за положением этой целевой линии. Это делается с помощью последовательного изображения этой линии, места танкера и одновременно положения танкера относительно сторон света. Далее делается скриншот экрана программы, именно он представлен на рис. 4. Это положение судна на 3 250 сек моделирования. В левой части рисунка показаны две траектории слежения за целью с разными начальными курсами танкера. Синий кружок показывает положение самого танкера, желтая прямая линия является в данный момент прицельной линией. Изображение справа дает положение танкера относительно сторон света, положение пера руля (синий отрезок), направление вектора скорости (оранжевая линия в ЦТ танкера) и целевой линии (желтая прямая выше танкера). Видно, что руль положен на правый борт для выхода на прицельную линию. Через скриншот проглядывает основное окно программы, на котором выводится информация о моделировании. На рис. 5 показан скриншот экрана программы моделирования для другого начального курса танкера в 310°. Выбран другой момент процесса моделирования, поэтому на рис. 5 справа мы видим другое относительное расположение танкера и прицельной линии. Она ниже танкера, и его руль положен на левый борт для выхода на эту линию.

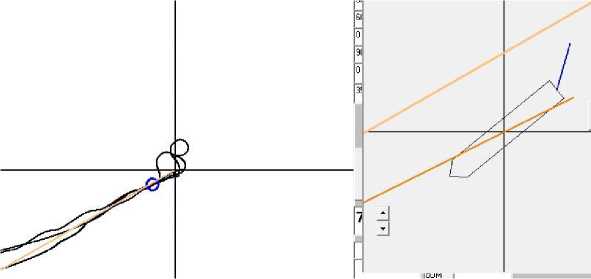
Рис. 4. Скриншот экрана программы моделирования в среде VB6

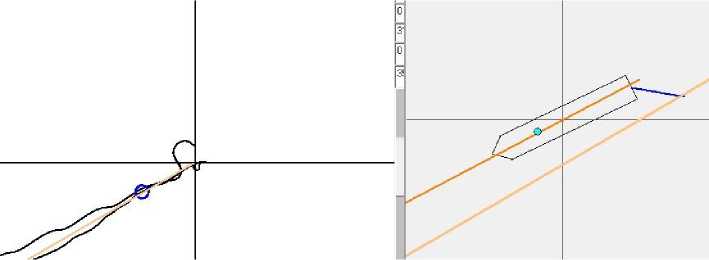
Рис. 5. Скриншот экрана программы моделирования в среде VB6 с начальным курсом танкера 310°

4.    Заключение

Результаты проведенного эксперимента показывают, что компьютерная модель судна успешно следит за прицельной линией, и каждый раз при смещении линии смоделированное судно движется за ней. Это позволяет сделать вывод, что реальное судно, управляемое предложенным способом, сможет точно так же сблизиться со швартующим судном и безопасно ошвартоваться. Следовательно, предложенный способ позволяет достичь поставленной цели автоматизации швартовки в полной мере.