Моделирование процесса швартовки к борту судна-партнера с использованием инновационного способа управления судном

Процесс швартовки одного судна к другому в открытом море – весьма распространенный вид судовых ключевых операций, сопряженный с риском столкновения швартующихся судов. Поэтому оптимизация процесса операций такого типа всегда была и будет актуальна. В данной статье авторы предлагают инновационный запатентованный способ швартовки одного судна к другому в условиях открытого моря. Описаны результаты модельного эксперимента, которые доказывают возможность применения данного способа на практике.

2.    Способ швартовки

Авторами разработан способ управления швартующимся судном при выполнении им швартовной операции к борту судна-партнера ( Юдин и др ., 2013a), когда в пределах контуров швартующегося судна и судна-партнера, в их диаметральных плоскостях выбирают по две точки, одна из которых находится на носовой части А (швартующееся судно), А_п (судно-партнер), другая – на кормовой части В (швартующееся судно), В_п (судно-партнер) относительно мидель-шпангоута соответствующего судна (рис. 1).

Координаты точек А , В , А_п , В_п в неподвижной координатной системе определяют непрерывно с высокой точностью (±1,0 м). Используя значения координат точек швартующегося судна А ( X 0 A , Y 0 A ) В ( X 0 B , Y 0 B ) и судна-партнера А п ( X 0 Aп , Y 0 Aп ), В п ( X 0 Вп , Y 0 Вп ) в неподвижной координатной системе, координаты тех же точек в подвижных системах координат, связанных c швартующимся судном А ( X_A , Y A ), В ( X B , Y B ) и судном-партнером А п ( X Aп , Y Aп ), В п ( X Вп , Y Вп ), координаты центров тяжести (ЦТ) швартующегося судна в связанной с ним подвижной координатной системе G ( X_G , Y_G ) и судна-партнера в связанной с ним подвижной координатной системе G п ( X 0 Gп , Y 0 Gп ), а также значения расстояния между диаметральными плоскостями (ДП) швартующихся судов h ₀ и расстояние между ЦТ швартующихся судов m рассчитывают ( Юдин и др ., 2013b):

• –    координаты центра тяжести швартующегося судна G ( X _{0 G} , Y _{0 G} ) в неподвижной координатной системе;

• –    координаты центра тяжести судна-партнера G п ( X 0 Gп , Y 0 Gп ) в неподвижной координатной системе;

• –    координаты точек А п ( Х А _п , Y_A п ) и В _п ( X_{B п} , Y_{B п} ), расположенных на перпендикулярах к ДП судна-партнера, восстановленных в точки А_п и В_п ;

• –    координаты проекции ЦТ судна-партнера G _п ( X _{0 G п} , Y _{0 G п} ) в неподвижной координатной системе на траекторию сближения в конечной стадии швартовки, проходящую параллельно ДП судна-партнера через точки A _п и В _п ;

• –    координаты второй заданной точки Р ₂( X _{0 P 2}, Y _{0 P 2}) в неподвижной координатной системе;

• –    текущее значение длины тормозного пути S _т;

• –    координаты первой заданной точки Р ₁( X _{0 P 1}, Y _{0 P 1}) в неподвижной координатной системе.

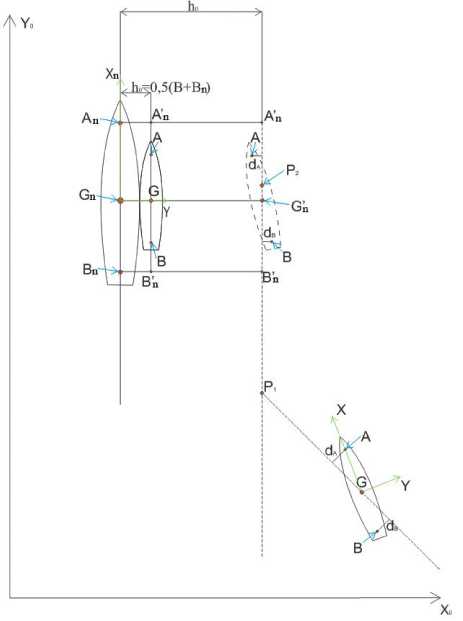
Рис. 1. Схема способа швартовки одного судна к другому в условиях открытого моря

Зная координаты первой заданной точки и координаты центра тяжести швартующегося судна, определяют текущее положение траектории сближения, проходящей через первую заданную точку Р ₁( X 0 P ь Y 0 P 1 ) и центр тяжести швартующегося судна G ( X 0 G , Y ₀ G ). После этого определяют поперечные смещения точек А и В от найденной указанным способом траектории сближения.

Непрерывно определяемые значения координат точек А и В , А п и В п позволяют непрерывно вычислять координаты центра тяжести швартующегося судна G , а вместе с непрерывно определяемым текущим значением длины тормозного пути S _т и координатами первой заданной точки Р ₁ - также поперечные смещения d A и d B точек А и В швартующегося судна от текущего положения траектории сближения ( Юдин, Пашенцев , 2012).

Возникающие поперечные смещения вырабатывают сигнал на отклонение рулевого органа, например руля швартующегося судна, по закону:

а = - kA х dA + k_B х d_B , (1) где k A , k_B - коэффициенты усиления по перечным смещениям носовой и кормовой точек швартующегося судна от текущего положения траектории сближения.

Таким образом, швартующееся судно движется по линии GP ₁ в направлении точки Р ₁.

В момент выхода швартующегося судна в первую заданную точку, что соответствует равенству координат центра тяжести швартующегося судна G ( X _{0 G} , Y _{0 G} ) и координат первой заданной точки Р ₁( X _{0 G} , Y ₀ P ₁) ( X _{0 G} = X _{0 Р 1}; Y 0G = Y ₀ P ₁), оно переходит к сближению со второй заданной точкой Р ₂, при этом текущее положение траектории сближения соответствует положению линии, проходящей через точки А п ( Х Ап , Y A _п ) и В_п ( X B _п , Y B _п ), координаты которых рассчитываются непрерывно. Текущие координаты второй заданной точки Р ₂( X ₀ P ₂, Y ₀ P ₂), лежащей на линии А_пВ_п , также вычисляются непрерывно.

Непрерывно определяемые значения координат точек А и В , А_п и В п позволяют непрерывно вычислять координаты точек А п и В_п , ЦТ швартующегося судна G и ЦТ судна-партнера G_п , второй заданной точки Р ₂ в неподвижной координатной системе, а также поперечные смещения d A и d_B точек А и В швартующегося судна от текущего положения траектории сближения, которой является линия А_пВ_п .

Возникающие поперечные смещения вырабатывают сигнал на отклонение рулевого органа, например руля швартующегося судна, по известному закону. Таким образом, швартующееся судно движется в точку Р ₂ по линии А_пВ_п .

Моментом окончания сближения швартующегося судна с судном-партнером считается момент выхода швартующегося судна во вторую заданную точку Р ₂, что соответствует равенству координат ЦТ швартующегося судна и второй заданной точки, т.е. X _{0 G} = X _{0 P 2}, Y _{0 G} = Y _{0 P 2}.

3.    Модельный эксперимент

Как было сказано выше, на первом этапе швартовки мы должны выйти в некоторую точку линии прицеливания, удаленную от цели на заданное расстояние. Координаты такой точки легко находятся по заданному расстоянию от цели Д и параметрическому уравнению линии прицеливания:

xx+ dd X cos( K ) + Д sin( K_z ); yx+ dd Xsin( K_z ) Д cos( K_z ).

Здесь dd 0 – параллельное смещение ЛП от цели, а параметры с индексом z относятся к самой цели. Управляющий сигнал формируется как пропорциональный отклонению курса судна от направления на переменную точки с координатами (2). Для судна результаты такого моделирования показаны на рис. 2. На данном рисунке показаны три пронумерованные траектории. Они отличаются координатами прицельной точки и начальными курсами судна. Начальная скорость хода одинакова и равна 3 м/с, ветра и волнения нет, время слежения 3 000 с (50 мин).

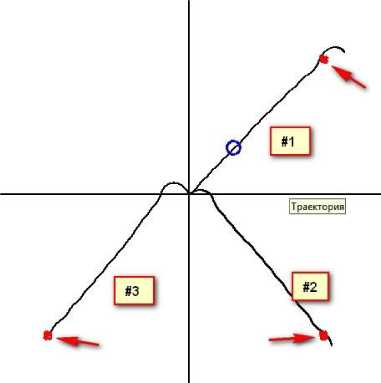
Рис. 2. Подход танкера к цели при управлении отклонением курса от направления на цель – траектории № 1, № 2, № 3

Данные по траекториям приведем в табл. 1. Стрелками показаны "облака" целевых точек. Они получены вариацией положения целевых точек в радиусе 250 м. Тем самым управление ведется по направлению на переменную точку.

Таблица 1. Данные по траектории

№ траект.	К 0 , град.	V 0 , м/с	Xц , м	Yц , м	Т , сек
1	55	3	5 000	5 000	3 000
2	65	3	5 000	–5000	3 000
3	320	3	–5000	–5000	3 000

Управление выбрано в соответствии с принятой стратегией: – управляющий сигнал sign – b × ΔК – с × d(ΔК) / dt, – скорость перекладки руля как функция управляющего сигнала v   0;

sign lim v    v                   1;

max lim lim

v max

sign     lim ;

lim sign lim ;

sign     lim .

Параметры этой стратегии управления выбраны такие:

b = 160, c = 400, lim ₁ = 3, lim ₂ = 14.

Они найдены путем подбора, оптимизацией управления с помощью принятых критериев. Процедуру этого подбора и результаты ее приведем ниже подробным образом. Фактически эта процедура – метод градиентного спуска ( Пашенцев, Юдин , 2013).

Здесь же опишем результаты проведенных модельных испытаний.

Из табл. 1 следует, что траектория № 1 имеет начальный курс 55 , целевая точка расположена на NE, поэтому управление не требует начального маневра. Две другие траектории приводят к необходимости начального маневра. Так, на траектории № 2 начальный курс судна равен 65 , а цель лежит на SE. Поэтому система управления производит начальный маневр и далее выходит на обычный режим управления. На траектории № 3 начальный курс 320 , цель расположена на SW, поэтому здесь также возникает начальный маневр. Главное в этих испытаниях состоит в том, что система управления во всех случаях работает правильно, и движение к цели завершается выходом к целевой точке. Но, возможно, при ручном управлении этот начальный маневр можно произвести более эффективно, и только после его выполнения перейти на управление автоматическое. Траектории № 2, 3 приведены для того, чтобы показать работоспособность системы управления по отклонению курса от направления на цель в этих сложных случаях, хотя в жизненной ситуации судоводитель произведет начальный маневр вручную, а затем включит систему управления. Показатели качества управления вычислены вдоль траектории № 1, они равны Q ₁ = 0.2168, Q ₂ = 0.0070. По двум другим траекториям показатели не вычислялись, т.к. нам нежелателен вклад начального маневра, который формально ухудшит эти показатели. Более того, показатели рассчитывались по 2 500 точкам, а не по всем 3 000. Дело в том, что когда судно проходит область целевых точек, действующая система управления начинает поворачивать судно назад. Этот поворот хорошо виден на траектории № 1 вблизи концевой точки. Разумеется, в этот момент в реальности система управления либо выключается с переходом на ручное управление либо происходит переход на другую стратегию управления.

На рис. 3-5 показаны в графической форме основные параметры, сопровождающие движение танкера вдоль траектории № 1. Так, на рис. 3 приведены изменения курса судна, угловой скорости поворота, кладки руля и угла дрейфа в градусах (или град/с). На рис. 4 – изменение продольной и поперечной скорости судна, скорости перекладки руля и сама траектория № 1. Зачернения на рис. 4 вызваны плотностью шкалы времени, эти участки отражают области с частым изменением скорости перекладки руля. Поэтому на рис. 5 приведены скорости перекладки руля для двух диапазонов времени: от 0 до 100 сек и от 2 000 до 2 100 сек, т.е. оба диапазона имеют длительность всего 100 сек. Здесь хорошо виден характер изменений скорости перекладки руля в процессе работы системы управления.

При моделировании проверена работа системы управления при возникающих возмущениях. Для этого на 1 000 сек в процесс моделирования были внесены точечные изменения угловой скорости и угла дрейфа, примерно пятикратные, причем угол дрейфа изменился даже по знаку. Система справилась с этими возмущениями и, отработав их, продолжила обычное управление примерно через 250 сек. Изменения кинематических параметров и траектории при этом возмущении приведены на рис. 6. Изменение скорости перекладки руля показано на рисунке в растянутой шкале от 990 до 1 500 сек (нижний график). На нем хорошо видна длительная выдержка руля в крайнем положении на левом борту. Реально таких возмущений быть не должно, но моделирование позволяет создавать

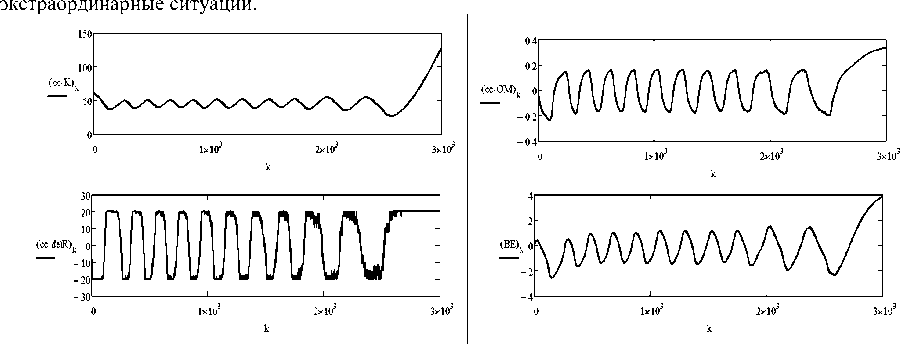
Рис. 3. Изменение курса судна, угловой скорости поворота, кладки руля и угла дрейфа на траектории № 1 танкера

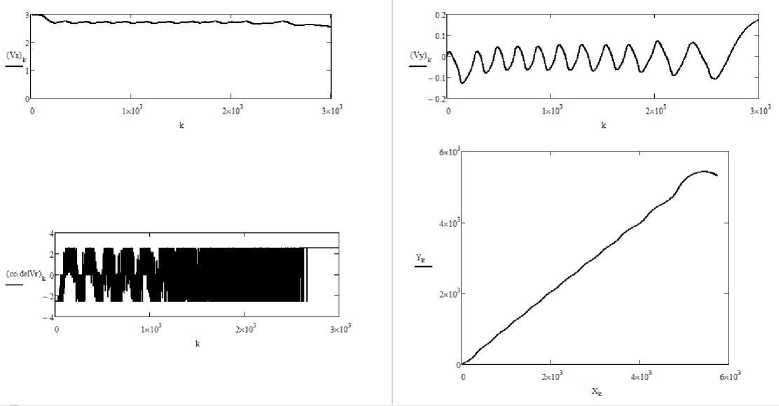
Рис. 4. Изменение продольной и поперечной скорости судна, скорости перекладки руля на траектории № 1 танкера

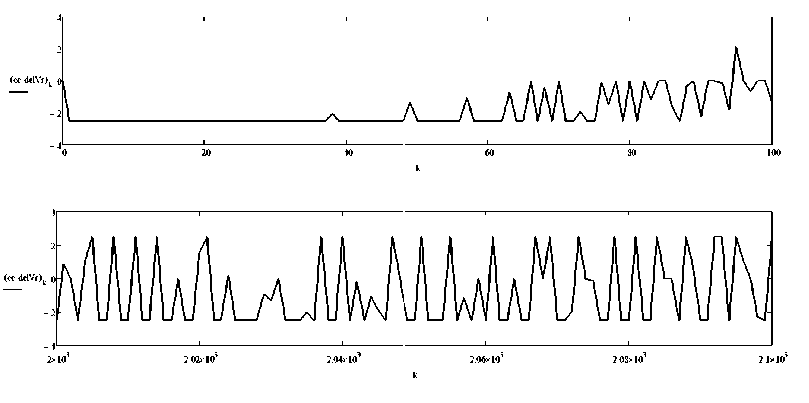
Рис. 5. Изменение скорости перекладки руля от 0 до 100 сек и от 2000 до 2 100 сек на траектории № 1 танкера

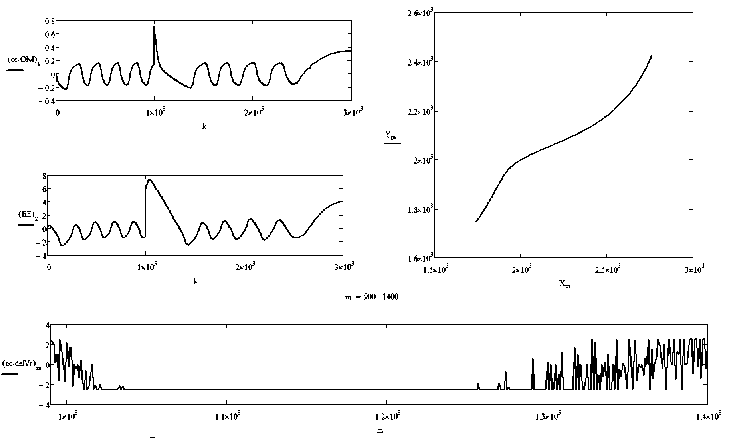
Рис. 6. Результаты отработки системой управления возмущений угловой скорости и угла дрейфа на 1 000 сек

Показав возможности данной стратегии управления, вернемся к проблеме синтеза, т.е. выбора параметров управляющей системы. Это коэффициенты усиления b и c в законе выработки управляющего сигнала и параметры lim 1 и lim 2 в законе выработки скорости поворота руля v α по управляющему сигналу sign . Для их определения был выбран метод покоординатного спуска при поиске экстремума показателей качества Q 1 или Q 2 . Проведено 11 опытов моделирования работы системы управления на базе траектории № 1 с изменениями синтезируемых параметров. Результаты такого моделирования приводятся в табл. 2.

Таблица 2. Результаты моделирования на базе траектории № 1

b	c	lim 1	lim 2	Q 1	Q 2
120	400	3	14	0.2245	0.0071
150	400	3	14	0.2222	0.0070
160	400	3	14	0.2168	0.0070
170	400	3	14	0.2320	0.0071
160	400	3	16	0.2270	0.0071
160	400	3	15	0.2305	0.0071
160	400	3	13	0.2260	0.0071
160	500	3	14	0.2311	0.0072
160	300	3	14	0.2328	0.0073
160	400	2	14	0.2223	0.0070
160	400	4	14	0.2271	0.0071

Последовательный анализ полученных данных позволил выбрать набор параметров из третьей строки табл. 2: b = 160, c = 14, lim 1 = 3, lim 2 = 14, с которыми и проводились все остальные моделирования работы системы управления.

Приведем на рис. 7 траекторию танкера с начальным курсом 240° и продолжительностью моделирования движения 7 000 сек. В начале траектории действие системы управления вызывает почти полную циркуляцию с тем, чтобы взять курс на целевую область на NE.

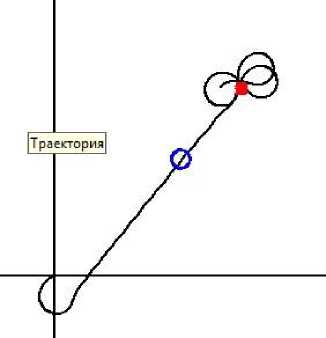
Рис. 7. Траектория танкера при начальном курсе 240° и продолжительностью движения 7 000 сек

Во время слежения за объектом в течение 3 000 сек поведение судна вблизи цели было видно не всегда. Здесь время моделирования взято равным 7 000 сек, поэтому поведение судна вблизи целевой области хорошо прослеживается. Судно под действием системы управления делает около трех циркуляций, возвращаясь каждый раз в целевую область. Необходимо подчеркнуть, что данным утверждением только демонстрируется поведение системы управления в модели. В реальности в этом случае судоводитель перейдет к ручному управлению судном.

4.    Заключение

Авторами предложен инновационный и запатентованный способ швартовки одного судна к другому в условиях открытого моря. Представлен результат модельного эксперимента, проведенного с целью доказать возможность применения способа на практике. На основании представленных данных можно с уверенностью сказать, что предложенный авторами способ управления судами при швартовке одного судна к другому в условиях открытого моря может быть использован для автоматизации данной операции, что и было доказано в расчетах.