Моделирование процесса сушки древесного сырья для последующего использования его при копчении рыбы

Во многих странах мира уже достаточно давно ведутся работы по изучению использования альтернативных возобновляемых источников энергии, например таких, как биомасса (древесные отходы, щепа, гранулы из древесины). Процесс сушки древесного сырья включен в технологические процессы производства некоторых продуктов питания, например, при копчении и сушке рыбы [1].

В России подобные исследования также набирают ход. На качественное и стабильное горение биомассы влияет её влажность. В настоящей работе предлагается модель для изучения процесса сушки древесины с целью определения его продолжительности, необходимой для достижения нужного уровня влажности материала.

Метод решения задачи

Процесс сушки древесной коры происходит при следующих условиях: кора имеет форму бесконечного плоского слоя заданной толщины; осуществляется принудительный нагрев конвекцией высокотемпературного газа одной из сторон этого слоя. В начале процесса кора имеет повышенную влажность. Процесс заканчивается, когда кора становится «достаточно» сухой. Параметры древесины в процессе сушки изменяются, так как зависят от влажности материала [2–4].

Для изучения процесса сушки древесной коры можно предложить следующую математическую модель, основанную на уравнении теплопроводности:

dU  dd c • p--= — (2),

5t   5x5

где U = U ( x , t ) – температура материала в точке с координатой x в момент времени t ; x изменяется от 0 до S ; время t от 0 до некоторого момента t k , здесь S – толщина древесного слоя. Следовательно, область интегрирования уравнения (1) задаётся неравенствами:

0 <  x <  S ; 0 <  t <  t_k (2)

Зададим начальное условие (начальное распределение температуры вдоль оси x ): при t = 0

U ( x ,0) = u o ,                 (3)

и граничные условия: при x = 0

² . = ^{a (}u max ^- U ),

при x = S

2 U = 0, 5 x

В формулах (1)–(5) используются следующие параметры: с – эффективная теплоёмкость; p - плотность материала, U = U ( x , t ) -температура участка коры с координатой x в момент времени t ; 2 - коэффициент теплопроводности; а - коэффициент теплоотдачи; A U = U d - U w > 0 - интервал температур, где U_d – температура «сухой» зоны материала, U_w – температура «влажной» зоны. Предполагается, что в начальный момент времени весь материал сырой и его температура не превосходит U_w .

Затем начинается обдув одной из поверхностей коры горячим газом, что приводит к её нагреву и постепенному «высыханию». При этом параметры модели с, p , 2 меняются по некоторым заданным законам. Процесс сушки должен завершиться при достижении некоторого заданного уровня содержания влаги в материале.

Обозначим через у долю влажного материала. Очевидно, что у может непрерывно изменяться от 1 (весь материал влажный) до 0 (весь материал сухой). Закон изменения у можно выбрать в виде:

' 1, U <  U w ;

у = Т

U d - U U d - U w ’

U w <  U <  U d ;

0, U >  U d .

Те участки коры, где температура U <  U_w считаются полностью влажными, а там где U >  U d - материал полностью сухой.

Эффективная теплоёмкость можно определить следующим образом:

C = т

C w ,   U <  U w ;

C w • у + C d • (1 - у ),    U w <  U <  U d ; (7)

C d ,    U >  U d .

где с w , с d – теплоёмкости влажного и сухого материала; g – доля влаги в элементарном объёме сухого материала; L – удельная теплота испарения влаги.

Коэффициент теплопроводности материала определяется по формуле:

2 w ,   U <  U w ;

² = T ² w • ^{у + 2} d • ^{(1 - у} ),

U w <  U <  U d ; (8)

\2 d ,    U >  U d .

где 2 w , 2 d - коэффициенты теплопроводности влажного и сухого материала.

Плотность материала определяется по формуле:

P w ,   U <  U w ;

p =T P w • у + P d • ^{(1 -} у ),

U w <  U <  U d ; (9)

I p d ,    u >  U d .

где p w , p d - плотности влажного и сухого материала.

Решение уравнения (1) при рассмотренных ограничениях (3)–(5) с учётом зависимостей (7)–(9) может быть получено только численно. Мы предлагаем использовать явную схему метода конечных разностей. Полученное решение при этом будет условно устойчивым.

Учитывая зависимость А = А( U ( х , t )) в виде (8) можно выразить

дЛ d Л д U

---_---;

dx dU д х

U” ⁺¹ _ и” +^—

1       1    cрhh

дЛ

д U

+ Л

U j + 1

Un j+1

—

\ 2 u^j к j

h

— 2 U ” + U ” ₁

Тогда уравнение (1) можно записать в виде:

дU дЛ дU , d^U c • р--=---+ Л--., д t   дх дх      дх2

к

к

h ²

или, с учётом (10), в виде:

д U  дЛ ,д U c • р--=--(--- д t   д U vaх

^ и .  (11)

д х х

дЛ

Для вычисления--будем использовать д U зависимость А = А( у (U)):

В формуле (17) индекс j изменяется от 2 до J -1. Для вычисления значений U в точках с индексами ( п + 1, 1) и ( п + 1, J) надо использовать граничные условия (4) и (5).

Рассмотрим граничное условие при х = 0. Разложим U ( х , t ) в ряд Тейлора в точке х = h:

U ( h , t ) _ U (0, t ) +

, д U

+ h--- д х

х _ 0

h ² д ² U

+--- 7Т

2 д х²

х _ 0

+ o ( h ² );

дЛ _ дЛ ду _ (Xw - Лd) _ АЛ д U " ду 'a U ” (Uw - Ud) = А U ’  (12)

А Л _ Л _а - Л w

из формулы (18) выразим

д U

д х

х _ 0

U ₂ ⁿ - U^j h

h 82U

—

2 д х ²

.

х _ 0

Проведём разбиение области интегрирования (2) следующим образом: равномерно разобьём отрезок [0, А ] с помощью J узлов по переменной х ; равномерно разобьём отрезок [0, t k ] с помощью N узлов по переменной t . Вычислим шаг h по переменной х и шаг А t по времени t :

Из уравнения (11) найдём

д ² U   1

—2-_— I c • р-- д х² Л к       д t

д U   дЛ д ) U

—

, 2

д U  д х

и подставим выражение (20), вычисленное при х = 0, в (19):

h _ А /( J - 1), А t _ t k /( N - 1).    (13)

д U

U j

—

и 1 ^j

—

Узлы сетки по t и по х :

д х

х _ 0

h

t n _ ( n - 1) •А t , n _ 1.. N ;

X j _ ( j - 1), j _ 1.. J .

Функцию U вычисленную в узле сетки (t n , X j ) обозначим U n

Заменим в уравнении (11) производные функции U ( х , t ) по формулам:

д U

д х

h 1

—

2 Л

c P к

U 0 ⁺¹

—

^U j    дЛ f ^иj

—

—

U L ^к 2 ^к

А t

д U

h

Подставим

х _ 0

выражение производной

в краевое условие (4):

f U j

—

u j

к

—

д U ^ U n ⁺¹ - U n _;   д U ^ U n+ 1 - U n _;

д t       А t    ’8х        h д2U ~ U 1 - 2и + Un- 1

д х ² ~ h ²

Подставим эти выражения в уравнение (11):

Un+1 - Un   дЛ c • р • —----- _

А t д U h

U" ,-2Un + Un, +Л ( j+1

h

—

—

Un

—)² +

Используя значения U j ₊₁ , U j , U j -1 в слое t = t n из соотношения (16) можно найти значение U^j+1 в слое t n+1 :

h

h 1

—

к

2 Л

U j cр —

—

I+1

—

А t

U j

—

_ а( и х max

—

и j ), (22)

дЛ Г и j

к д U

—

U j

h

Выразим из (22) U j ⁺¹ :

и^{j + 1} _ U^j +^ t-c • р

—

2.a

—(U, -u ) +

1    ^max

h

+ 2^( U j - U j ) + h

дЛ

+--- д U

( U j

—

h

и j к ²

Формула (23) позволяет вычислить значение функции U в левом конце интервала при x = 0 в момент t = t +Δ t , если известны значения U в момент времени t при x = 0 и x = h.

Рассмотрим теперь граничное условие при x = S . Поступим аналогичным образом, разложим U ( x , t ) в ряд Тейлора в точке x = S при заданном t :

U ( S - h , t ) = U ( S , t ) -

, 5 U

- h-- dx x=S h2 52U

+---7

2 5 x ²

+ o ( h 2 )

модели, массивы времени t и координаты x . Функция nаgrеv2 проводит вычисления температуры в узлах сетки в соответствии с формулами (17), (23) и (27). Функция param вычисляет параметры модели в соответствии с формулами (6)–(9). Нужно отметить, что начальное распределение температуры вдоль оси x может быть нераномерным, т. е. оператор под номером 24 в функции nаgrеv2 можно задать так, что значения u (0, x ), будут меняться по заданному закону. Например,

Выразим из (24)

a и a x

а и _ и ( s , t ) - и ( s - h , t ) +

5x x _ s             h h a2и     un- и" h a2и

+_ JJ _1 +

2 ax2           h 2 ax x x _ S                             x

u (1,1: J ) _ u 0

x (1: J) - 0.25 Y x (J)    J

x u 0 + 0.1 ou 0;

u (1,1: J ) _ u 0 abs

f x (1: J) - 0.25 Y v    x(J)    J

x u 0 + 0.1 u 0;

.      „ 82и

Значение ax x найдём из уравнения

(11) при x = S , учитывая краевое условие (5):

а 2u _ c • p а и dx2   „ x at x _ S

~ c • p U J ^{+ 1} - и J ,

~ X     ^ t'

Подставим (26) в (25), учитывая, что

*= 0:

• ^d x x _ S

• и" - и" _x h f c • p и","' - и"\ _n

• J - 1 +•          J _ 0;

• h 2 ( X      At

Выразим иг1:ип+ _ип+ 2хA^(uJ-1 -uJ). (27) h cp

Формулы (17), (23) и (27) задают вычислительный процесс для определения температуры U ( x , t +Δ t ) при известных значениях U ( x , t ).

Для компьютерного моделирования процесса сушки была разработана программа в среде Matlab (см. приложение)

Программа работает в соответствии с алгоритмом, описанным выше. Основная программа формирует вектор параметров

Функция (28) – «перевёрнутая» парабола, сдвинутая вверх на 1.1u0 и вправо по оси x на 0.25. Функция (29) – «модуль» x , сдвинутый вверх на 1.1u0 и вправо по оси x на 0.25.

Расчёты проводились при следующих значениях исходных данных: время t = 0.60 С, число дискретов 201; для переменной x толщина слоя древесины S = 0.5, число дискретов 21; при x = 0 температура обдува 126 градусов; коэффициент теплоотдачи а = 20; начальное распределение температуры при t = 0: u0 = 30; температура влажной и сухой зоны: U w = 40 и U d = 80; теплоёмкость влажной и сухой древесины с w = 3.6 и C d = 2.2; плотность влажной и сухой древесины p w = 600 и p d = 400; теплопроводность влажной и сухой древесины X w = 0.35 и X d = 0.20.

На рисунке 1 представлены графики изменения температуры вдоль оси ОХ через равнее промежутки времени (0.3 с) от 0 до 60 при: a) постоянном u0 = 30 начальном значении температуры; b) при начальном распределении температуры в соответствии с формулой (28); c) при начальном распределении температуры в соответствии с формулой (29): d) при начальном значении, равном конечному распределению температуры, полученном в 1 случае, но «перевёрнутым» относительно оси ОХ. Это процесс сушки древесины, при котором древесина сушится сначала с одной, а затем с другой стороны.

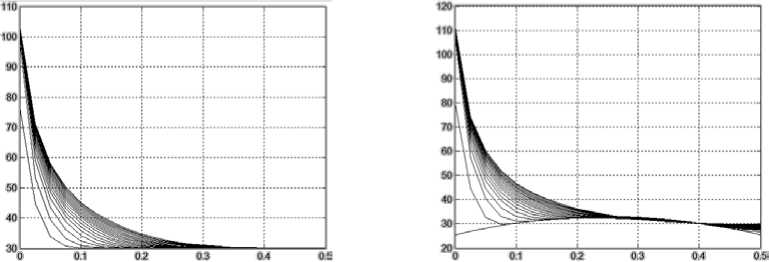
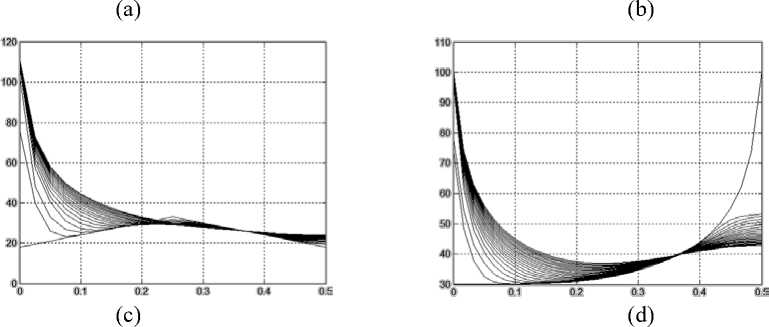
Рисунок 1. Графики изменения температуры вдоль оси ОХ

Figure 1. Graphs of temperature variation along the axis OX

Результаты и обсуждение

На основе полученных расчётных формул (17), (23) и (27) написана программа в среде МatLаb и проведено компьютерное моделирование процесса сушки древесины. Результаты работы программы для различных начальных условий распределения представлены в виде графиков распределения температуры u ( t , x ) (ось OY) вдоль оси ОХ при различных значениях времени t .

Важным моментом подобных расчётов является выбор шага дискретизации по времени t и пространственной переменной x [5–6]. В этом варианте использовалась явная схема сеточного метода, которая является условно устойчивой. В условиях классической постановки задачи для уравнения теплопроводности с постоянными коэффициентами шаг по x и по t рекомендуется выбирать так, чтобы значение выражения (1–2s) было положительным, где s = k • Dt / ( Dx )², а коэффициент k - удельная теплопроводность материала. Это означает, что s < 0.5 и шаги по t и по x должны быть согласованы. Для этой задачи выбор шага по t и по x делается путём подбора, так как коэффициенты модели меняются.

В качестве дальнейшего развития данной модели можно разработать алгоритм моделирования процесса сушки с применением метода прогонки – это будет неявная схема решения задачи, но более устойчивая. Кроме этого, можно аппроксимировать кусочно-линейные зависимости (7)–(9) с помощью гладких зависимостей типа «арктангенс», что также должно улучшить качество процесса моделирования процесса сушки.

Заключение

В результате проведенного исследования разработана модель процесса сушки древесины, которая, в частности, может быть использована для изготовления коптильных сред, используемых далее по назначению. Модель может быть использована в системах автоматического управления при альтернативных технологиях получения энергии с использованием биомассы.

Выражаем благодарность к.т.н., профессору А.М. Прохоренкову за постановку задачи и консультации в ходе выполнения работы и д.т.н., профессору Ю.В. Шокиной за консультации в области физических свойств древесины и обсуждение полученных результатов.

Приложение

• 1.    % основная программа моделирования процесса сушки startnagrev2.m

• 2.    S=0.5; % толщина слоя по х

• 3.    tmax=60; % интервал времени по t

• 4.    kmax=201; % количество дискретов по

• 5.    xv=linspace(0,S,21);

• 6.    tv=linspace(0,tmax,kmax);

• 7.    vpar(1)=126; % температура обдува

• 8.    vpar(2)=20;  % alfa = коэфф. теплоот

• 9.    vpar(3)= 30; % начальное распределение температуры вдоль х

• 10.    vpar(4)= 40; % температура влажной зоны

• 11.    vpar(5)= 80; % температура сухой зоны

• 12.    vpar(6)= 3.6 % теплоёмкость влажной древесины

• 13.    vpar(7)= 2.2 % теплоёмкость сухой древесины

• 14.    vpar(8)= 600 % плотность влажной древесины

• 15.    vpar(9)= 400 % плотность сухой древесины

• 16.    vpar(10)= 0.35 % теплопроводность влажной древесины

• 17.    vpar(11)= 0.200 % теплопроводность сухой древесины

• 18.    uv=nagrev2(tv,xv,vpar);

• 19.    prn3d=input('введите 1 для формирования графика 3D = ');

• 20.    if prn3d==1

• 21.    surf(xv,tv,uv)

• 22.    xlabel x;

• 23.    ylabel t;

• 24.    zlabel U(x,t);

• 25.    else

• 26.    k=1;

• 27.    while k

• 28.    plot(xv,uv(k,:),'k-')

• 29.    hold on

• 30.    k=k+10;

• 31.    end;

• 32.    end;

• 33.    %plot(xv,uv(200,:),'r-')

• 34.    grid on

t;

дачи

1.    function u = nagrev2(t,x,vp) 2.    % здесь проводятся вычисления в соответствии с алгоритмом 3.    % см. формулы (17), (23) и (27) 4.    umax=vp(1); %температура обдува 5.    alf=vp(2); % коэфф. теплоотдачи 6.    u0=vp(3); % начальное распределение температуры вдоль х 7.    u1=vp(4); % температура влажной зоны 8.    u2=vp(5); % температура сухой зоны 9.   ------------------ весины