Моделирование процесса ультразвуковой окорки лесоматериалов

• -    разработать структурную схему комплексной модели технических систем и технологии окорки лесоматериалов ультразвуком;

• -    разработать математическую модель технических систем, предназначенных для окорки лесоматериалов ультразвуком в водной среде.

Методика и результаты исследований. Комплексная модель технических систем и технологии окорки лесоматериалов ультразвуком разрабатывается по трём основным направлениям (рис. 1) [1]:

• -    математическое моделирование технических систем;

• -    математическое моделирование процессов, протекающих при ультразвуковой окорке лесоматериалов;

• -    концептуальное моделирование технолого-экологических аспектов ультразвуковой окорки лесоматериалов.

Основываясь на структуре комплексного моделирования окорки лесоматериалов ультразвуком, разработку модели можно ориентировать по принципу технического дифференцирования, позволяющего исследовать параметры отдельно каждого элемента технической системы. В связи с этим ниже представлены математические модели ультразвукового генератора и колебательной системы.

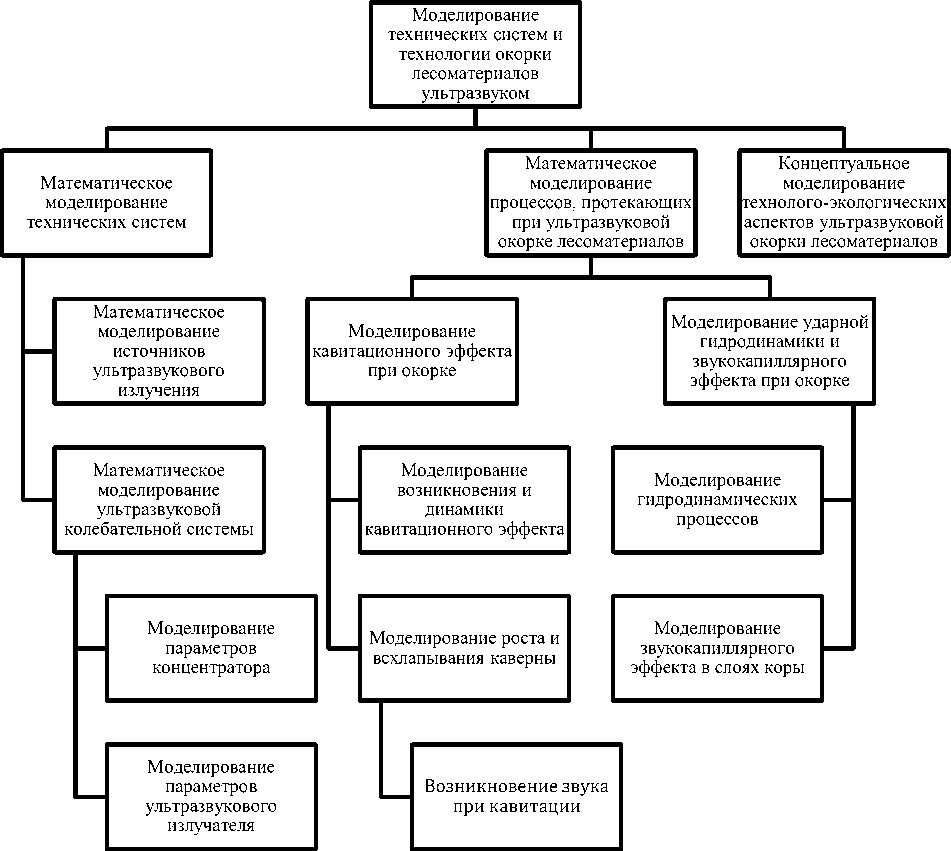
Рис. 1. Структура комплексной модели технических систем и технологии окорки лесоматериалов ультразвуком

При рассмотрении колебаний упругих тел будем полагать, что материал тела однороден, изотропен и подчиняется закону Гука.

При выводе уравнения движения будем основываться на гипотезе плоских сечений. Кроме того, будем игнорировать силы инерции, связанные с поперечными движениями частиц стержня при его растяжении – сжатии. Тогда положение каждого поперечного сечения в процессе движения полностью характеризуется его продольным смещением U .

Рассмотрим элемент стержня, ограниченный двумя поперечными сечениями (рис. 2) [1]. Обозначим:

N – поперечная сила в сечении, Н;

dJ – сила инерции, кг·м/с²;

F(Z) - площадь поперечного сечения, м 2 ;

U(Z) - смещение данного поперечного сечения вдоль оси бруса Z , мм;

Е- модуль упругости материала стержня (модуль Юнга), Н/м;

• р - плотность материала стержня, кг/м³;

• о - круговая частота, рад/с;

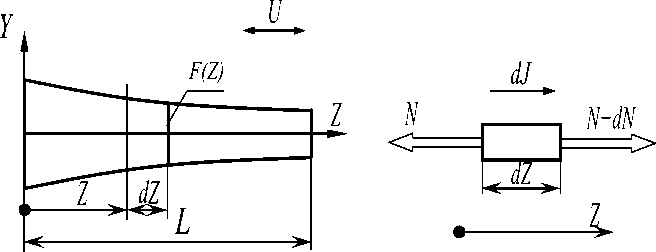
Рис. 2. Элемент стержня, ограниченный двумя поперечными сечениями

Сила инерции выражается следующим образом [1, 2]:

_ d 2U _ dJ = - pF (Z )—r dZ dt2

.

При стационарных колебаниях с круговой частотой о :

dJ = о2 • р • F (Z) • U (Z) dZ

(1а)

Сравнение системы дифференциальных уравнений, описывающих продольные колебания записывается в соответствии с законом Гука.

* dZ                           Левое сечение элемента смещается вдоль оси Z на

^                   U, правое - на величину U+dU (рис. 3). Таким образом, абсолютное удлинение элемента равно:

∆L=U + ∂U dZ-U = ∂U dZ, ∂Z        ∂Z а относительное

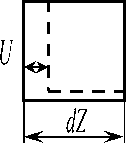
Рис. 3. Левое сечение элемента

∆L ∂U ε=   = dZ ∂Z

Усилие, возникающее в сечении, связано с относительным удлинением законом Гука для одноосного напряжённого состояния:

dU

N = EF (Z )s = EF (Z) —

∂ Z

.

Окончательно система дифференциальных уравнений, описывающая свободные продольные колебания стержней переменного сечения, запишется в виде:

'д U — = { дZ ’ д N 1 д Z

1 , . =------N ( Z ) EF ( Z )            .                                      (4) = - ®2 p- F ( Z )U ( Z )

Волновое уравнение продольных колебаний такого стержня имеет вид:

На основании данной системы уравнений можно определить рациональные параметры концентратора и разработать элементы установки для окорки лесоматериалов ультразвуком [2].

На основе предложенной модели кавитирующей среды разработана методика расчета предельных параметров электронных генераторов ультразвуковых технологических аппаратов, таких, как запас мощности и диапазон изменения частоты, для работы с жидкими средами при условии реализации в них режима развитой кавитации.

Для оптимизации параметров ультразвуковой окорки круглых лесоматериалов возникает необходимость разработки математической модели различных процессов, происходящих при реализации технологии. Ультразвуковая окорка является сложной системой процессов, происходящих при воздействии ультразвуковых волн на различные участки слоёв коры и среды окаривания.

При исследовании показателей ультразвука основным принципом физического влияния на элементы коры является процесс возникновения кавитационного эффекта, позволяющего синтезировать различные процессы для отрыва коры от древесины. Учитывая это, разработаны математические модели возникновения кавитационного эффекта при ультразвуковой окорке, возникновении гидродинамических процессов, влияющих на физический отрыв коры от древесины.

Одним из факторов эффективной ультразвуковой окорки лесоматериалов являются показатели кавитационного эффекта, возникающего в области действия ультразвука. В связи с этим необходимо разработать комплексную модель возникновения кавитационного эффекта с параметрированием показателей возникающей при этом энергии [4,5].

Кавитационный эффект, возникающий в зоне разрушения элементов и слоёв коры, можно условно дифференцировать на два этапа: возникновение и динамика; рост и схлопывание кавитационного пузырька. Так как процесс ультразвуковой окорки происходит в водной среде, то при возникновении и динамике каверны формируются гидродинамические течения, а при схлопывании выделяется энергия, разрушающая слои коры.

Исследования акустической кавитации позволяют получать наиболее адекватные результаты по воспроизводимости условий эксперимента, а также дают возможность проведения измерений физических параметров в кавитационной области. Заметим, что близкие по природе физико-химические эффекты имеют место и при целом ряде воздействий другой физической природы, таких, как лазерная кавитация, гидродинамическая кавитация, электрогидравлический взрыв, ударное механическое воздействие на взвесь пузырьков в жидкости и т.п. Тем не менее устоявшаяся акустическая терминология широко используется и в настоящее время, поэтому мы также будем пользоваться этими общепринятыми терминами.

Энергия запасается при расширении пузырька от равновесного радиуса R до максимального радиуса R max под воздействием растягивающих сил, возникающих в жидкости в фазе разрежения акустической волны. Величину запасенной энергии можно оценить как W = А V • P 0 , где А V - изменение объёма пузырька при уменьшении его радиуса с R max до R mm , P o - давление в окружающей жидкости, которое при акустической кавитации можно принять равным статическому давлению. Если принять условие R max >>  R min , что обычно имеет место при кавитации, то для энергии получим

3 ,

W = - nR max • P o .                                 (6)

Явление кумуляции энергии кавитационным пузырьком на качественном уровне легко объяснимо. Эффект заключается в том, что первоначально запасенная энергия преобразуется вначале в кинетическую энергию жидкости, сферически-симметричное движение которой по направлению к центру пузырька обуславливает бесконечное (для вакуумного пузырька) увеличение скорости сжатия, что выражается в появлении сингулярностей в решениях гидродинамических уравнений.

Впервые математическое описание процесса сжатия кавитационного пузырька получил Рэлей [3]. Он исследовал динамику пустого (вакуумного) пузырька, причем его модель учитывала только инерциальные силы и пренебрегала вязкостью, поверхностным натяжением жидкости и давлением парогазовой смеси внутри пузырька и имела вид:

RR + ^- R ² =— ⁰ .                          (7)

2 Р

При начальных условиях:

R (t ) = Ro; R (t ) = Ro , где R(t) - текущий радиус пузырька, а точки обозначают производные по времени t; Ро - статическое давление в жидкости; р - плотность жидкости.

Учет давления газа в пузырьке и изменяющегося давления в жидкости, а также вязкости и поверхностного натяжения, позволяет получить более универсальное уравнение динамики кавитационного пузырька, называемое уравнением Рэлея-Плессета::

АЛ rR + -R2 = - Pg -Po -p(t)-^-р = o.          (8)

2 Ру        RR J где Pg - давление газовой смеси в пузырьке, Па; P(t) - внешнее переменное давление, Па; р - коэффициент вязкости жидкости; ст - коэффициент поверхностного натяжения жидкости.

Уравнение Рэлея-Плессета хорошо описывает динамику пульсаций газового пузырька в процессе его расширения и большей части фазы сжатия.

Критерием перехода от сжатия с бесконечно возрастающей скоростью к сжатию за бесконечное время служит число Рейнольдса:

Re = —. Ж.                        (9)

Р \ Р

При Re > Re* (малая вязкость), где Re* - некоторое критическое число, скорость границы полости R неограниченно возрастает при R > 0 по такому же закону, как и в задаче Рэлея; R ~ R-3/2, но с меньшим значением коэффициента пропорциональности (часть энергии превращается в тепло за счет диссипации). При Re < Re* (большая вязкость) вязкость сильно препятствует ускорению жидкости, захлопывание пузырька происходит медленно, за бесконечное время. Кумуляция энергии, характерная для задачи Рэлея, отсутст- вует. В промежуточном случае при Re = Re* пузырек захлопывается за конечное время; скорость R при R >0 неограниченно растет, но слабее, чем R-1. Численное интегрирование уравнений динамики пузырька дает для критического числа Рейнольдса значение Re* = 8,4. Для данной жидкости, находящейся под данным давлением, т. е. при заданных р, /л и Ро, можно говорить критическом радиусе пузырька R*. При Ro < R* кумуляция полностью устраняется вязкостью. Реально критический радиус чрезвычайно мал, например, для воды R*=0,8 мкм. Уравнение (10) более точно описывает динамику кавитационного пузырька с учетом сжимаемости, но только до скоростей движения, сравнимых со скоростью звука в жидкости с о:

( 2 -Y- 3

(          7

1 - -³- R Ri ² +

V    ^{4 c} о 7

^{R 1} - - R ^R + -

V c о 7     ²

+ —

р

P 0

2 -   4 ^ R

-

(

P 0

V

+ 2 - Y ^{R   3}

R 0 )V R )

+ .

+

P c о

■

RR

I ' - 7 R 1 d

V    c о ) d^R

= 0.

< dZ dN i d^Z

_ dZ

EF ( Z ) • 1 +

EF ( Z ) • 1 +

- ®² p F ( Z )U 1

- ®² p F ( Z )U ₂

^ 0

4n2

V 0

4n2

N 1 + ^^ N 1

У 2лю )

N - ^^ n 2 о       1

у    2яю )

На конечной стадии захлопывания пузырька скорость его стенки может превышать с о . В этом случае применяется уравнение Кирквуда-Бете [5], выведенное с допущением о сферичности волн конечной амплитуды, образующихся при схлопывании полости:

где

(       2 .7--

R 1-- R R + - 1

V

^c о  7

1 •

• •

•

-

—R R ² +

V

1 •

+ R 1 + —R H--R 1

V     ^c о

c ₀

-

^{4 c} о 7

- R ⁷ RdH = о,

dH

.

V    c о 7

dR

P ⁽ R >

H = dP =

P р Л

п   A n

-----Y--1n - 1 р

(

P 0

V

2—^+ ~R '

^R о 7

( R А ^{3 3}

R 0

-

n - 1

V R 7

+ B

R

n

-

-

( Р _о - P m sin © • t + B ) n

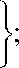
с = ^{[ с} о ² + ( ^{п -} 0 ^H ] 2

где А , В , n - постоянные коэффициенты, значения которых для воды А = 300 МПа, B = 300 МПа, n = 7.

Выводы. Таким образом, на основании разработанной комплексной модели можно определить показатели технических систем, технологий и технологических комплексов окорки лесоматериалов ультразвуком в водной среде. Это позволит разработать комплекс рекомендаций по реализации технологического процесса ультразвуковой окорки лесоматериалов.