Моделирование процесса уплотнения щебеночно-песчаной смеси методом укатки

В связных грунтах, в которых силы внутреннего трения незначительны, а физико-механические, электрохимические и водно-коллоидные сцепления между мелкими частицами существенно выше и являются преобладающими, главным действующим фактором служит сила давления или напряжения сжатия и сдвига, а роль первого фактора становится второстепенной.

Динамическая модель напряженно-деформированного состояния щебеночно-песчаной смеси приведена на рисунке 1 [1, 2].

с т

о

Рис. 1. Реологическая модель процесса уплотнения щебеночно-песчаной смеси:

E M ,η M – модуль деформации и вязкость смеси (максвелловская); E К ,η К – модуль деформации и вязкость смеси (кельвиновская); с ( ^ ) - повышение предела текучести смеси; о 1 , о 2 - напряжения

Элемент жесткого трения a ( s ) характеризует повышение предела текучести смеси с ростом ее плотности.

Уплотняющее давление а определяется суммой напряжений в вязких элементах в моделях Фойгта-Кельвина и Максвелла

а = а + а 2.

Напряженное состояние щебеночно-песчаной смеси создается в результате деформирования уплотняющими нагрузками. Поведение реологической модели процесса уплотнения (рис. 1) описывается дифференциальными уравнениями [1]

_ 1 da     а - Cd

ПкС--—+ EK --+ а1 = Пк — + EKs a1 tg^ at       a1 tg^

Пм.^а₌ „ dS

+ C 2   ''M’

EM dtdt

а1 + a2 = a- где EК ,ηК – модуль деформации и вязкость смеси (кельвиновская); EM ,ηM – модуль деформации и вязкость смеси (максвелловская); a1, a 2 - напряжения смеси: С - сопротивление сдвигу смеси; ф - угол внутреннего трения материала; ε – деформация смеси.

Непосредственный анализ системы (2) представляет определенную сложность. В связи с этим решение дифференциальных уравнений можно реализовать при известных параметрах п _м , П _к , E M , E K , V , C на ЭВМ программой MATLAB SIMULINK и построить графические зависимости: s = f . ( t ) ; a ₁ = f 2 ( t ) .

Приведем систему дифференциальных уравнений (2) к виду Коши

da,  ar'tqpr   ds        a -C-C

-?■=—П11 ^+Eks-E  .— a1];

dt    nkC    k dt          k atqv

da2  Em ds

= — [П —-C 2]. dt am m dt

Модель динамического равновесия системы, набранная в системе «Matlab+ Simulink», приведена на рисунке 2.

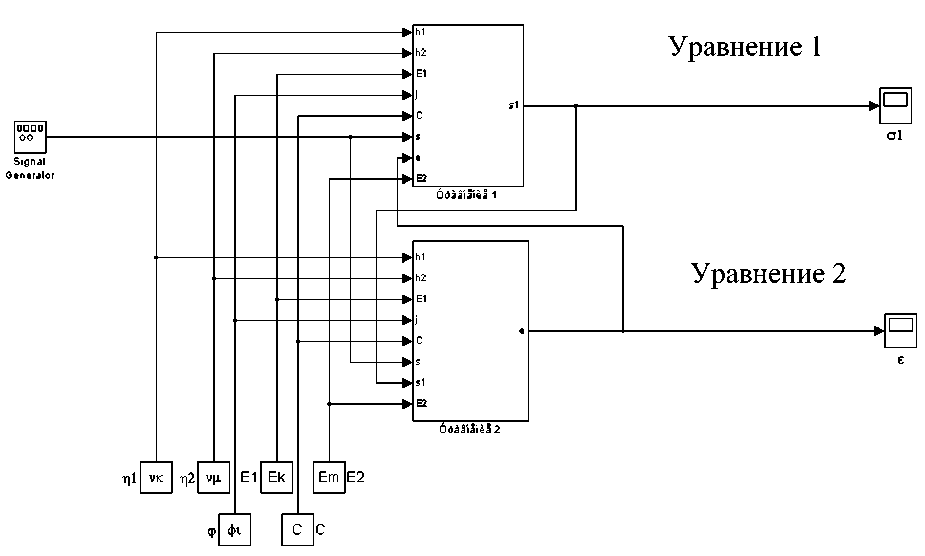
Рис. 2. Модель динамического равновесия системы

Блок-схемы уравнений динамического равновесия системы приведены на рисунках 3 и 4.

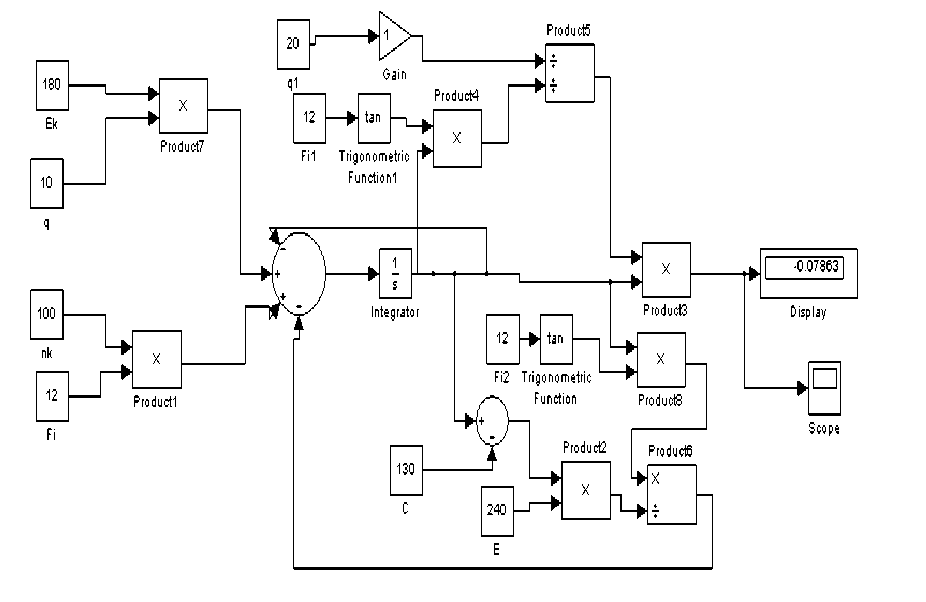
Рис. 3. Блок-схема уравнения (1) динамического равновесия системы

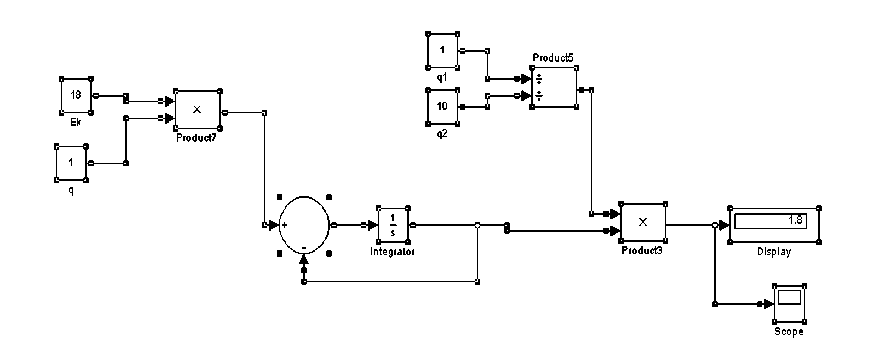
Рис. 4. Блок-схема уравнения (2) динамического равновесия системы

Начальными условиями рассматриваемой системы являются параметры, приведенные в таблице.

Начальные условия рассматриваемой системы

Тип смеси	Е к	η к	Е м	η м	σ 1	σ 2	С	φ
Для покрытий (ГОСТ 25607-94)	3789	0,04	7056	1,1	28	42	0,09	45
Для оснований (ГОСТ 25607-94)	4267	0,05	8345	1,2	29	46	0,10	43
Из шлаков (ГОСТ 3344-83)	4589	0,06	9753	1,3	30	47	0,11	42

Примечание. E К ,η К – модуль деформации и вязкость смеси (кельвиновская); E M ,η M – модуль деформации и вязкость смеси (максвелловская); & 1 , а 2 - напряжения смеси: С - сопротивление сдвигу смеси; ф - угол внутреннего трения материала; ε – деформация смеси.

Результаты исследования напряженно-деформированного состояния щебеночно-песчаной смеси приведены на рисунке 5.

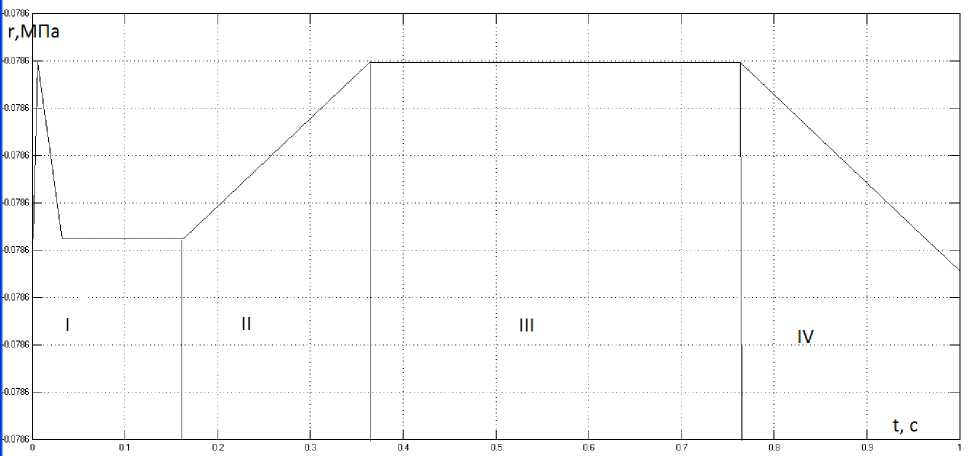
Рис. 5. Графическая зависимость напряжения щебеночно-песчаной смеси, без учета остаточной деформации

Процесс уплотнения щебеночно-песчаной смеси состоит из четырех стадий. В первом периоде происходит его деформирование и равномерное распределение прочности. Во второй период происходит набор прочности смеси. Дальнейшее уплотнение смеси в третьем периоде протекает в равномерном режиме. При снятии нагрузки происходит релаксация напряжений в четвертом периоде, что определяет необходимость дополнительного уплотнения смеси.

Выводы. Продолжительность периода зависит от частоты колебаний ТБ, оказывает влияние на скорость деформирования материала и соответствующее ей реактивное сопротивление, а также определяет время, в течение которого происходит релаксация напряжений. Для повышения качества уплотнения щебеночно-песчаной смеси необходимо дополнительное уплотнение.