Моделирование процесса возникновения тяжей в эластомерных композитах

ВЕСТНИК ПНИПУ. МЕХАНИКА № 2, 2019PNRPU MECHANICS BULLETIN

С начала XX века известно, что наполнение каучуков (эластомерных материалов) техническим углеродом (20– 30 % по объему) существенно улучшает многие их эксплуатационные свойства: повышает жесткость, увеличивает разрывные усилия в 5–15 раз, а предельные деформации в 2–4 раза. В настоящее время продолжают интенсивно проводиться исследования механических свойств эластомерных нанокомпозитов в зависимости от вида наполнителя, его концентрации и технологии изготовления. Примером могут служить работы, связанные с изучением свойств эластомеров, заполненных такими наполнителями, как сажа, углеродные нанотрубки, наноалмазы, различные минеральные частицы (монтмориллонит, палыгорскит, шунгит и т.д.) [1–8]. Одновременно с экспериментальными ведутся и теоретические исследованиями по структурному моделированию физико-механических свойств материалов с учетом особенностей внутреннего строения и процессов на микро- и наноуровне [9–15] и др.

Важной особенностью эластомерных композитов является изменение их свойств в результате предварительного деформирования (эффект Маллинза) [16–20]. Этот эффект может оказывать значительное влияние на поведение изделий из наполненного эластомера [21]. На сегодняшний день эффект Маллинза является объектом интенсивного теоретического и экспериментального изучения. В литературе до сих пор нет единого устоявшегося мнения о его природе. Чаще всего этот эффект связывают с развитием поврежденности материала.

Однако, несмотря на несомненный прогресс в анализе возможных механизмов формирования свойств нанона-полненных эластомеров, еще остается ряд до сих пор нерешенных вопросов. Объяснить повышение прочности и появление анизотропных свойств после первого деформирования можно существованием микро- и нановолокон (тяжей). Наличие таких образований подтверждается экспериментально [22–27]. В работе [28] на основе экспериментальных исследований структуры наполненных техническим углеродом резин (использовалась электронная микротомография) и компьютерного моделирования показано, что при макродеформациях до 15 % микродеформации матрицы в зонах между агломератами частиц сажи могут достигать 100 и более процентов. Исследования наноструктуры наполненных каучуков в растянутом (вплоть до предразрывного) состоянии методами атомносиловой микроскопии [29, 30] подтвердили наличие таких образований. Томограммы микроструктуры резины (электронная микроскопия), полученные в работе [31], также показывают и тяжи, и соединяемые ими агрегаты из сажевых частиц.

В данной работе рассматривается одна из возможных гипотез, объясняющая эффект повышения прочности наполненного эластомера.

1.    Критерий возникновения микроповреждений в наполненных эластомерах

Целью исследования является проведение вычислительного эксперимента, с помощью которого анализируется разумность гипотезы, что в зазорах между близкорасположенными частицами наполнителя эластомерная матрица при деформировании материала способна выдерживать очень высокие нагрузки. Происходить это может по следующей причине. В ненагруженном состоянии полимерные цепи свернуты в клубки. При растяжении материала в одном направлении полимерные цепи разворачиваются и ориентируются вдоль оси действующей нагрузки. Возникает состояние эластомерного материала, в котором произошла ориентация большинства цепей в одном направлении. В случае частично кристаллизующегося полимера в таких областях будут возникать кристаллиты (зоны повышенной жесткости с упорядоченно уложенными молекулярными цепочками, в которых межмолекулярные силы связывают их в жесткое образование). Если же полимер рассматривается как некри-сталлизующийся эластомер, то жестких надмолекулярных образований в нем не возникает. Тем не менее есть все основания считать, что преимущественная ориентация полимерных цепей вдоль одной общей оси дает эластомерной матрице способность выдерживать более высокую нагрузку в направлении ориентации, чем в других нагруженных состояниях с той же самой интенсивностью деформаций.

Для того чтобы количественно определять момент появления повреждения в эластомерном композите с учетом этого фактора, необходим соответствующий прочностной критерий. Мы предлагаем использовать новый критерий прочности в виде следующего условия: в рассматриваемой точке материала не может произойти разрушение, если выполняется неравенство

f (Xi, Xv Х3 ) =

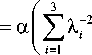
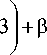
X,   X2   Х3

ln ¹ln ² ln ³

X ₂   X   X

+ Y p <  1,

где X i - кратность удлинений; p - среднее напряжение (первый инвариант тензора напряжений Коши, деленный на 3).

Деформационный критерий прочности содержит две безразмерные α, β и одну размерную γ константы, определяющие прочностные свойства материала. Их значения можно подобрать из экспериментов. Первое слагаемое дает ненулевой вклад в критерий (1) при любом деформированном состоянии материала. Второе слагаемое при одноосном растяжении материала равно нулю. При других видах напряженно-деформированного состояния оно дает дополнительный положительный вклад в функцию f . При этом добавка может быть весьма значительной, если значение параметра β достаточно велико. Третье слагаемое учитывает тот факт, что при всестороннем сжатии материала повреждениям появиться значительно труднее.

На рис. 1 представлена карта распределения значений / (X₁,X 2, X₃) для несжимаемой среды (то есть случай, когда X₃ = (X । X₂) ¹ однозначно определяется через X i и X₂). Область, где выполняется условие f(X 1 ,X₂,X₃) < 1 (разрушение невозможно), показана серым цветом. Зоны, где f(X 1 ,X₂,X₃) >  1 (разрушение должно произойти), заштрихованы (рис. 1, a ). Три сплошные линии на рисунке соответствуют одноосному растяжению по каждой из главных осей. Карта построена для следующих значений констант: а = 0,25; в = 0,05; у = 0, которые были использованы в дальнейшем для вычислительного моделирования. Из анализа этой карты видно, что при одноосном растяжении материала можно его деформировать до очень больших значений. В других видах напряженно-деформированного состояния разрушение начнется при существенно меньших деформациях.

Главная особенность предлагаемого критерия состоит в том, что при одноосном растяжении значение функции f минимально по сравнению с другими видами напряженно-деформированного состояния (рис. 1, б) при одних и тех же значениях инварианта тензора деформации I = X - ² + X - ² + X - ² и величине среднего напряжения p .

Наиболее важным в механике композиционных материалов является анализ парного взаимодействия близкорасположенных включений (рис. 2) [32, 33]. Целью вычислительного эксперимента является определение условия появления повреждений около пары включений, нагруженных силами, приложенными к центрам частиц и действующими в противоположных направлениях вдоль оси, соединяющей центры частиц.

В рассматриваемой задаче использованы следующие геометрические соотношения. Вычисления осуществлены для цилиндрической ячейки, в которой размещалась пара жестких сфер радиусом R . Включения располагались на оси симметрии на расстоянии 5₀ друг от друга. Высота цилиндра и диаметр цилиндрической ячейки задавались равными 15 R . Таким образом, обеспечивалось условие отсутствия влияния удаленных границ на напряженно-деформированное состояние вокруг данной пары. Внешние границы структурной ячейки считались свободными от напряжений. Нагружение системы производили за счет раздвигания сфер вдоль межцентровой оси на заданное расстояние δ. В качестве меры, характеризующей макроскопические деформации при парном взаимодействии включений, использована величина X = (5+2 R ) / (5 0 +2 R ).

Все приводимые в данной работе расчеты показаны для случая, когда начальный зазор между частицами 50 равнялся 0,4R. Выбор этого значения был сделан из тех соображений, что на данном расстоянии градиенты напряжений в зазоре еще не столь велики, чтобы создавать технические сложности при решении задачи, и в то же время «взаимное влияние» между частицами уже вполне достаточно для наших целей (моделирование процесса возникновения микротяжей) [34]. При уменьшении величины зазора, при одинаковом растяжении центров включений, значительно увеличиваются деформации в зазоре. Это означает, что в таком материале тяжи начнут формироваться раньше.

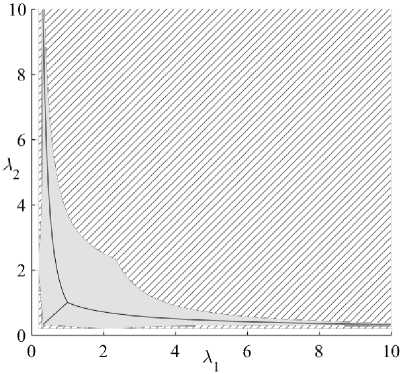
Рис. 1. Значение критерия f : a – иллюстрация карты состояний, в которых не появляются повреждения (область, закрашенная серым цветом), и состояний, где должны возникнуть микроразрывы (заштрихованные области); б – поле распределения значений параметра f . Сплошные линии соответствуют условию одноосного растяжения материала

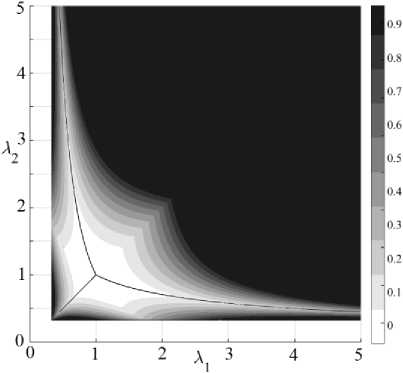
б

Fig. 1. The value of the criterion f ; a – a map illustrating the states where no damages (shown in grey) occur and the states where microdamages should happen (shaded areas); b – Fields of distribution of parameter f values. Solid curves correspond to uniaxial tensile loading conditions

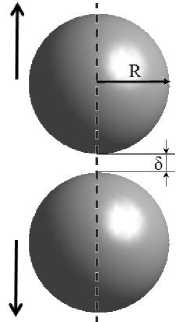
Рис. 2. Расчетная схема задачи о двух жестких с ферических включениях в нелинейно-упругой матрице

Fig. 2. Calculation scheme of the problem of two rigid spherical inclusions in a nonlinear elastic matrix

Предполагалось, что адгезионная прочность контакта между дисперсной фазой и континуумом намного превышает прочность матрицы (отслоения исключены), то есть на границах «матрица – включение» задавалось условие полной адгезии. Жесткость частиц наполнителя в упрочняемых эластомерных композитах, как правило, намного выше, чем у матрицы. Поэтому упругий модуль сферических включений E p задавали равным 10⁴ E m , то есть включения при расчетах были практически неде-формируемыми и неразрушаемыми. Повреждения могли возникать только в эластомере. Матрицу считали несжимаемой нелинейно-упругой средой. Ее механические свойства описывали с помощью потенциала Неогука:

w = E m ( X 2 + X 2 +X₃² - 3 ) . (2)

Краевую нелинейно-упругую задачу решали методом конечных элементов в осесимметричной постановке.

2.    Результаты вычислительного моделирования

Решение вышеописанной краевой задачи с применением часто употребляемых прочностных критериев (разрушение при превышении предельных значений таких инвариантов напряженно-деформированного состояния, как максимальные интенсивности напряжений или деформаций, главные напряжения или деформации, гидростатические напряжения) показало, что во всех этих случаях разрыв связующего должен происходить в зазоре между включениями, то есть никаких тяжей там появиться не может.

Иная картина наблюдается при использовании нового критерия. Компьютерное моделирование процесса развития локального повреждения производилось следующим образом. В процессе пошагового нагружения цилиндрической ячейки для каждого конечного элемента рассчитывалось значение f(λ1, λ2, λ3), и в случае f > 1 его модуль уменьшался до близкого к нулю значения. Тем самым имитировалось «разрушение» этого элемента. Расчеты показали, что первоначальные разрывы матрицы происходят не в зазоре, а на некотором удалении от него. При этом дальнейший рост возникших повреждений при увеличении растягивающей внешней нагрузки также не затрагивает центральную часть зазора. Вокруг него образуется «полая» кольцевая область.

На рис. 3 приведены изолинии значений параметра f , соответствующие следующим моментам формирования нанотяжа в материале: при λ = 2 пара включений растянута, но повреждений в эластомере еще нет (рис. 3, a ); при λ = 2,17 возникают первичные повреждения в матрице (рис. 3, б ); при λ = 2,34 идет процесс формирования области разрушения в направлении, параллельном линии, соединяющей центры включений (рис. 3, в ). Если продолжить моделирование процесса нагружения, то в итоге формируется одноосно растянутый «тяж», соединяющий поверхности частиц наполнителя. Вокруг него находится область разрушенного связующего. Разрушенные области показаны на рис. 3 белым цветом.

Представленный выше вариант компьютерного исследования не учитывает ряд факторов, которые могут играть важную роль при формировании тяжей. На протяжении второй половины ХХ века было много высказываний и косвенных подтверждений особых свойств связующего около частиц наполнителя. В частности, высказана гипотеза, что свободные радикалы на сколах частиц технического углерода вызывают химическую реакцию, которая приводит к появлению на поверхности частиц слоя «связанного» полимера с повышенной жесткостью [35]. В результате химической реакции, идущей от поверхности частиц наполнителя, в таких слоях повышается количество сшивок между полимерными цепями. Все это способствует повышению жесткости материала матрицы вблизи частиц.

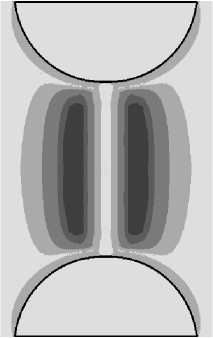
Рис. 3. Поля распределения значений параметра f в зазоре между частицами (однородная эластомерная матрица): ( a ) λ = 2; ( б ) λ = 2,2; ( в ) λ = 2,4

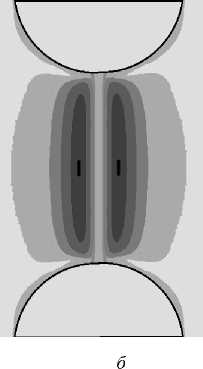
Fig. 3. Fields of distribution of parameter f values in the gap between the particles (homogeneous elastomeric matrix): ( a ) λ = 2; ( b ) λ = 2.2; ( с ) λ = 2.4

Для качественной оценки влияния этого фактора на процесс локального разрушения были проведены аналогичные модельные исследования для случая, когда полимер в зазоре неоднороден по механическим свойствам. Неогуковая матрица в зазоре состоит из кольцевых областей с увеличивающимися по мере приближения к центру жесткостями. Начальный модуль матрицы на оси симметрии в зазоре E g послойно повышается от E m до 1,4 E m . Расчетная схема представлена на рис. 4.

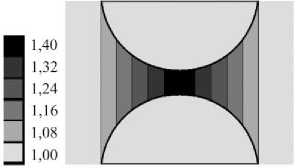
Рис. 4. Карты распределения начального модуля Юнга матрицы в зазоре E g ( E g увеличивается до 1,4 E m )

Fig. 4. Maps of distribution of the initial Young's modulus of the matrix in the gap E g ( E g increases to 1.4 E m )

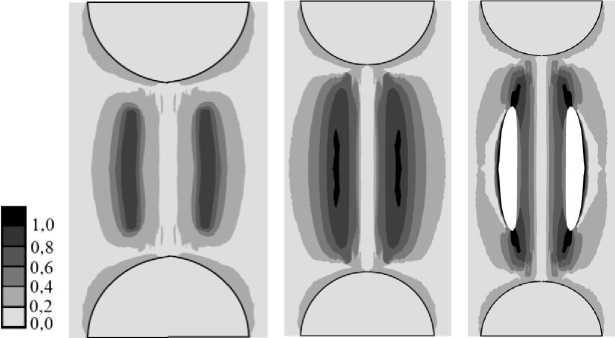
На рис. 5 приведены изолинии значений параметра f для этого случая. Для удобства сравнения результатов с вариантом для однородной матрицы (см. рис. 3) представлены ситуации для λ = 2,0; 2,2 и 2,4. Расчеты показали, что в этом случае процесс возникновения и роста локальной поврежденности протекает практически так же, как и для гомогенной матрицы. Толщины образовавшихся тяжей также оказались близки, то есть увеличение жесткости матрицы в зазоре частиц слабо сказывается на формировании тяжей.

Компьютерные эксперименты показали разумность гипотезы об особом характере развития внутренней по-врежденности в дисперсно наполненных эластомерах. Наличие жестких и прочных частиц наполнителя способствует появлению и формированию нанотяжей в местах локальной концентрации микронапряжений (в зазорах между включениями). Эти микротяжи принимают на себя значительную часть несущей нагрузки материала, что препятствует быстрому «прорастанию» макроразрывов, как это происходит в чистом эластомере. Именно это обстоятельство может служить одним из самых правдоподобных объяснений хорошо известного экспери- ментального факта, что прочность и предельная дефор-мативность эластомерных композитов может быть существенно выше, чем чистой матрицы.

а                         б                      в

Рис. 5. Поля распределения значений параметра f в зазоре между частицами ( E g увеличивается до 1,4 E m ): ( a ) λ = 2; ( б ) λ = 2,2; ( в ) λ = 2,4

Fig. 5. Fields of distribution of parameter f values in the gap between the particles ( E g is increased to 1.4 E m ): ( a ) λ = 2; ( b ) λ = 2,2; ( с ) λ = 2,4

Выводы

Предложен новый деформационный прочностной критерий, который позволяет описать механизм возникновения и развития структурной поврежденности в эластомерных нанокомпозитах. В основе его лежит известный факт, что при больших деформациях дисперсно наполненного эластомера связующее в зазорах между близко расположенными частицами наполнителя находится в напряженно-деформированном состоянии, близком к одноосному растяжению. При разработке критерия использована гипотеза, что при этом происходит переориентация полимерных молекул, и матрица в зазоре переходит в одноосно ориентированное состояние. В результате материал получает способность выдерживать более высокую нагрузку в направлении ориентации, чем в других нагруженных состояниях с той же самой интенсивностью деформаций.

Модельные расчеты показали, что такой подход позволяет теоретически описать процесс образования