Моделирование процессов образования и разложения газовых гидратов в пористой среде при депрессионном воздействии

• 1.    Введение

  Газовые гидраты представляют собой твёрдые кристаллические соединения молекул газа и воды, устойчивые при определённых давлениях и температурах. При диссоциации одного кубического метра газового гидрата выделяется до 180 м ³ газа и 0,8 м ³ воды ( Makogon , 2010). Природные газовые гидраты, состоящие в основном из гидрата метана, рассматриваются как перспективные источники углеводородного сырья. К настоящему времени газогидраты обнаружены в районах, расположенных вдоль побережий Северной и Южной Америки, Евроазиатского континента, в Австралии, Индии, Японии, под Чёрным, Каспийским и Средиземным морями, озером Байкал и др. По различным оценкам ресурсы природных газовых гидратов значительно превышают суммарные ресурсы всех горючих ископаемых. Поэтому актуальным является вопрос о поиске экономически рентабельных технологий разработки залежей газовых гидратов ( Makogon , 2010; Birchwood et al. , 2010). В настоящее время рассматриваются три основных метода добычи газа из гидратного пласта: понижение давления ниже равновесного, нагрев гидратосодержащих пород выше температуры разложения гидрата и их комбинация (рис. 1).

• 2.    Постановка задачи

  Для математического моделирования процесса объёмной диссоциации газовых гидратов в пористой среде было предложено две модели – равновесная и кинетическая. В основе первой модели лежит предположение о том, что в каждом элементарном объёме пористой среды выполняется условие термодинамического равновесия системы "газ – вода – гидрат" ( Бондарев и др. , 1976; Максимов, Цыпкин , 1990; Максимов , 1992; Бондарев, Попов , 2002; Нигматуллин и др. , 1998). Кинетическая модель основана на экспериментальной зависимости скорости диссоциации газогидрата от давления, температуры и размеров его частиц ( Kim et al ., 1987). В работе ( Kowalsky, Moridis , 2007) показано, что

• при численном моделировании процесса диссоциации газовых гидратов в пласте равновесная и кинетическая модели дают близкие результаты. Кроме того, отмечается, что использование равновесной модели предпочтительнее, так как она требует меньше вычислительных ресурсов.

Рис. 1. Фазовая диаграмма системы "газ – вода – гидрат" и возможные методы добычи газа из гидратов. 1 – депрессионное воздействие, 2 – тепловое воздействие, 3 – комбинированное воздействие

В данной работе рассматривается осесимметричная задача об отборе газа из пласта, насыщенного термодинамически равновесной смесью газа, воды и гидрата. Предполагается, что скелет пористой среды и газовый гидрат несжимаемы и неподвижны, вода несжимаема, движение газа и воды подчиняется закону Дарси, кровля и подошва пласта теплоизолированы.

Основные уравнения, описывающие динамику равновесной смеси газа, воды и гидрата в пористой среде, выводятся из законов сохранения массы и энергии ( Максимов , 1992; Бондарев, Попов , 2002; Нигматуллин и др. , 1998; Цыпкин , 2009). В радиальных координатах система уравнений имеет следующий вид ( Бондарев, Попов , 2002):

д T        d S_h    Л                   d p 1 d ( „ 9 T )

( p C ) mq P    - m ( 1 - S )( 1 - S>, ) P c П~r X +

‘e д t       ^Ph д t     ^V "^A               д t r д r V   д t J

+ k(Sh)p c fg^K,J) -k(S„)(p c ft- + p c f^-)A— = 0;(1)

h g g JT                   h g gw w g g и     l д r)           g g и и д r д r g                   V     g^gw

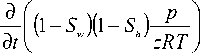
1 д ( k (Sh) f p дp)д r h h)js_p— mp„h_;

r д r и    zRT д r

V    g^sJ

m

1 (s (1 - s ))=1A wh д t              r д r

( _r ^{k ( S}h ) ^fw ^д P )

V    U w ^{д r} J

-

m ( 1 - s ) ^h- ^ S h , P w д t

где p – давление; T – температура; m – пористость; µ g , µ w – вязкость газа и воды; S w – водонасыщенность; S h – гидратонасыщенность; f g , f w – функции относительных фазовых проницаемостей для газа и воды; ρ g , ρ w , ρ h – плотность газа, воды и гидрата; ε – массовое содержание газа в гидрате; z – коэффициент сверхсжимаемости газа; ( ρC ) e – объёмная теплоёмкость скелета и вмещающих флюидов; c g , c w – теплоёмкость газа и воды; q – теплота фазового перехода гидрата; η – коэффициент адиабатического расширения; K JT – коэффициент Джоуля-Томсона; λ – коэффициент теплопроводности скелета и вмещающих флюидов.

Условие термодинамического равновесия смеси "газ – вода – гидрат" описывается эмпирическим уравнением ( Бондарев и др. , 1976):

T = a ln p + b ,                                         (4)

где a и b константы, определяемые экспериментально.

Предполагается, что в начальный момент времени пласт имеет гидратонасыщенность S h ⁰ , водонасыщенность S w ⁰ , равновесное давление p 0 и температуру T 0 = a ln p 0 + b . На контуре питания пласта поддерживается постоянное давление p 0 и температура T 0 . На забое скважины задаётся постоянное давление (депрессионный метод воздействия):

p ( r c ,t ) = p c .

Из решения системы нелинейных уравнений (1-4) находятся неизвестные значения функций p , T , S h и S w . Массовый дебит газа и воды в пластовых условиях определяется в виде:

Q s = 2 n Hk ( S_h )p_g ^U^r д Р-  ;

Q w = 2nHk ( S h ) p w, f^r |p   ,

Uw д r,=rc где rc – радиус скважины; H – толщина пласта.

Для численного решения данной задачи используется метод конечных разностей со сгущающейся в окрестности скважины сеткой узлов. Построение такой сетки осуществляется с помощью преобразования координат u = lnr (Азиз, Сеттари, 1982). Конечно-разностные аналоги уравнений (1-3)

имеют вид:

(pc J.

,-2 U i

Tⁿ i

n

T i + 1

_-

n - 1

_-

A t n

m n c g ( 1 — 5 " )( 1 - S h^ P g,^

2 T ⁿ + T ⁿ i            i - 1

h

+

k ( S n P

n

gi

fⁿ c ^g K JT e

g

g

n

_-

pi

n - 1

_-

.-2 u ,

A t n

'p p J

h

nn k ( S ,. J p c \ hi /I Гр g

f n _i

—— + p c .

w wi

P

g

fⁿ wi

A

P w J

e

.-2 u ,

i

pi

n

pi

n

i - 1

Tⁿ i

n

T i - 1

m

/

h

h

= mq p h

S

n

hi

S

n - 1

hi

A t n

, i = 1, m ;

^A t n

V

n

( 1 - Sⁿ J( 1 - S " J wi hi _n zRT ⁿ i

_-

(i - s:-J(i - s,

n - 1

hi

J-

P_i n - 1

zRT ^{- 1} i

m

A t n

= e

,^-2 u

= ^m P_h^e

S

n

hi

S

n - 1

hi

A t n

, i = 1, m ;

( S w ( 1 - S hi J - S " ^{- 1} ( 1 - S h - J J + m ( 1 - e J ^P

P w

S

n

hi

S

n - 1

hi

r

k ( S h J f w

P i +

p i ⁿ

A t n

P w

i + 12

h

e

,^-2 u

r

k ( S h J f w

P w

, - 112

p i ⁿ

h

p i ⁿ - 1

.

Система нелинейных уравнений (6-8) решается итерационно. Вычислительный алгоритм заключается в следующем:

• 1.    Из системы уравнений (7) методом потоковой прогонки находится распределение давления p .

• 2.    Из решения системы уравнений (8) определяется водонасыщенность S w .

• 3.    Если S"h ^{- 1} >  0, то с учётом условия термодинамического равновесия (4) из уравнений (6) определяется гидратонасыщенность на новом временном слое. В случае S h "^-1 = 0 из уравнений (6) находится распределение температуры.

• 3.    Результаты расчётов

  Расчёты проводились при следующих значениях параметров: p 0 = 10 МПа; p c = 5 МПа; S h ⁰ = 0,39; S w ⁰ = 0,21; r c = 0,1 м; R k = 500 м; H = 10 м; ρ w = 1000 кг/м ³ ; ρ h = 920 кг/м ³ ; m = 0,2; k 0 = 0,01 мкм ² ; N = 2; ^ w = 1 мПа/сек; ^_g = 0,013 мПа/сек; £ = 0,147; a = 7,28; b = 169,7 K; (pC) e = 1,48 Дж/(м ³ - К); X = 1,71 Вт/(м - К); c_g = 2093 Дж/(кг - К); c_w = 4200 Дж/(кг - К); c h = 3210 Дж/(кг - К); Кд- = 0,4 К/МПа; п = 0,14 К/МПа; q = 5,1 - 10 5 Дж/кг. Значения параметров для газа соответствуют чистому метану.

Коэффициент сверхсжимаемости газа вычисляется по формуле Латонова-Гуревича ( Бондарев, Попов , 2002):

z ⁽ P, ^{T J}= ⁰'^17376ln T^ ^{+ 0},⁷³

V

V кр 7

' t

+ 0,1     .

Для вычисления относительных фазовых проницаемостей газа и воды используются зависимости ( Максимов, Цыпкин , 1990):

f ( S w ) =

• ( 1 - S w /0,9Г ( 1 + 3 S w ) , 0 <  S w <  0,9,

• 0, S w >  0,9,

  f ( S ) = ww

  
  

(( S w - 0,2 ) /0,8 ) ^3,5 , 0,2 <  S w <  1,

0,0 <  S <  0,2. , w ,

Зависимость проницаемости от гидратонасыщенности принимается в виде ( Бондарев и др ., 1976;

Нигматуллин и др ., 1998):

k(Sh) = k0(1 – Sh)N, где k0 – абсолютная проницаемость породы в отсутствии гидрата.

На рис. 2 представлены графики распределения гидрато- и водонасыщенности в различные моменты времени. В результате разложения гидрата с течением времени водонасыщенность увеличивается по всему пласту, принимая максимальное значение за фронтом диссоциации.

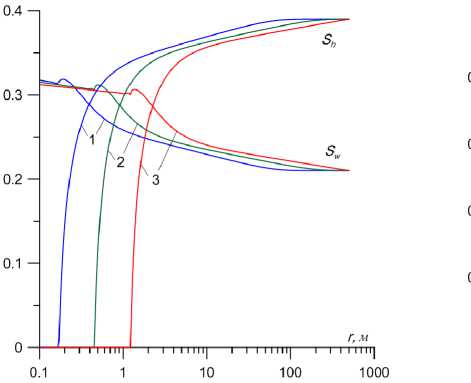
Рис. 2. Распределение гидрато- и водонасыщенности на моменты времени: 1 – 1 сут, 2 – 10 сут, 3 – 100 сут

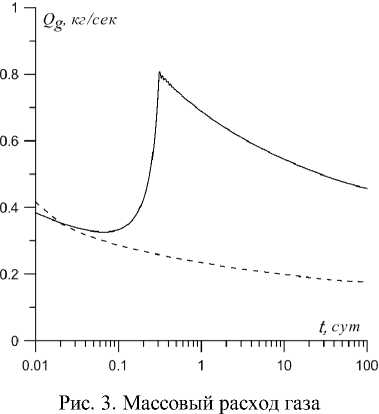
Графики изменения массового дебита газа с учётом (сплошная линия) и без учёта разложения газогидрата в пласте (пунктирная линия) представлены на рис. 3. Видно, что в результате диссоциации газогидрата в окрестности скважины зависимость массового расхода газа от времени имеет немонотонный характер.

Общий объём разложившегося гидрата определяется по формуле:

V h = 2 n H^m J r ⁽ S h ^- S h ⁽ r ) ^^r .

rc

Расчёты показали, что в результате диссоциации газового гидрата в течение ста суток из пласта дополнительно добывается порядка 10 ⁶ м ³ газа.

В процессе добычи газа при определённых термобарических условиях возможно вторичное образование газовых гидратов в окрестности скважины ( Бондарев, Попов , 2002). На рис. 4 представлены графики распределения гидрато- и водонасыщенности при начальном пластовом давлении p 0 = 20 МПа и забойном давлении p c = 15 МПа. В результате охлаждения газа вблизи скважины гидратонасыщенность начинает расти до тех пор, пока вся свободная вода не перейдёт в гидрат. В удалённой зоне пласта, как и в предыдущем примере, происходит диссоциация газогидрата. С ростом гидратонасыщенности в окрестности скважины фильтрационные свойства призабойной зоны ухудшаются. Зависимость массового расхода газа от времени представлена на рис. 5.

4. Заключение

В работе показано, что при депрессионном воздействии объём разложившегося гидрата незначителен по сравнению с общим объёмом гидрата в пласте. Поэтому для разработки газогидратной залежи более эффективным является сочетание депрессионного и теплового метода воздействия. Установлено, что при пуске скважины в газогидратном пласте зависимость массового расхода газа и воды от времени имеет немонотонный характер. Немонотонность кривых изменения массового расхода газа при пуске скважины может служить одним из диагностических признаков диссоциации газовых гидратов в пласте.

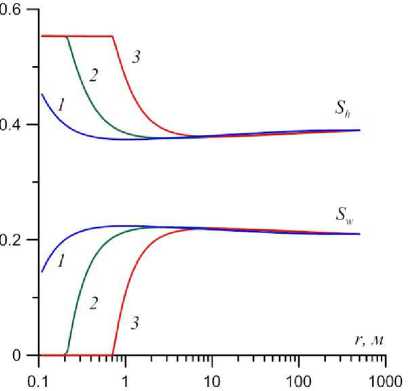
Рис. 4. Распределение гидрато- и водонасыщенности на моменты времени: 1 – 1 сут, 2– 10 сут, 3 – 100 сут

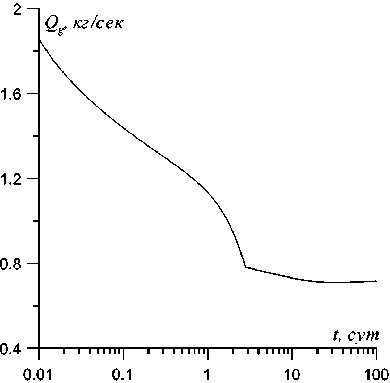
Рис. 5. Массовый расход газа

Работа выполнена при финансовой поддержке РФФИ (грант № 11-05-00878-а).