Моделирование процессов ползучести монокристаллических сплавов с учетом рафтинга

Никелевые жаропрочные монокристаллические сплавы [1; 2] представляют собой класс материалов с уникальными свойствами. К отличительным особенностям данного класса материалов можно отнести крайне высокие показатели длительной прочности и сопротивления высокотемпературной ползучести за счет отсутствия межзеренных границ [3], высокую стойкость к коррозии [1]. В то же время следует отметить анизотропию механических свойств [3–6], а также снижение, по сравнению с поликристаллическими материалами, термоинициированных напряжений и рост сопротивления малоцикловой усталости, обусловленные уменьшением модуля упругости в осевом направлении лопаток [4; 5]. Развитие газотурбинных двигателей (ГТД) неотрывно связано с повышением рабочих температур [7; 8] (рис. 1), что, в свою очередь, способствует развитию жаропрочных сплавов. Так, температура газа перед турбиной в двигателях пятого поколения, например в современном российском двигателе ПД-14 [9; 10], достигает 1850 K (1577 °С) [7]. Целевым показателем военных двигателей шестого поколения является достижение температуры 2350 K [7]. Современный российский монокристаллический сплав на никелевой основе ВЖМ4, применяемый для производства лопаток двигателей пятого поколения, в том числе ПД-14 [10], имеет стабильное структурное состояние вплоть до 1473 K (1250 °С) [11], что составляет примерно 90 % от температуры плавления материала [4]. Таким образом, в на- стоящее время монокристаллические никелевые сплавы являются практически безальтернативными материалами для лопаток газотурбинных двигателей 5-го и 6-го поколений [12]. На макроуровне монокристаллические сплавы на основе никеля обнаруживают свойства кубической симметрии, при которой механические свойства оказываются практически одинаковыми для трех взаимно перпендикулярных направлений.

Монокристаллические сплавы на никелевой основе представляет собой двухуровневый иерархически упорядоченный материал, свойства которого на макро-

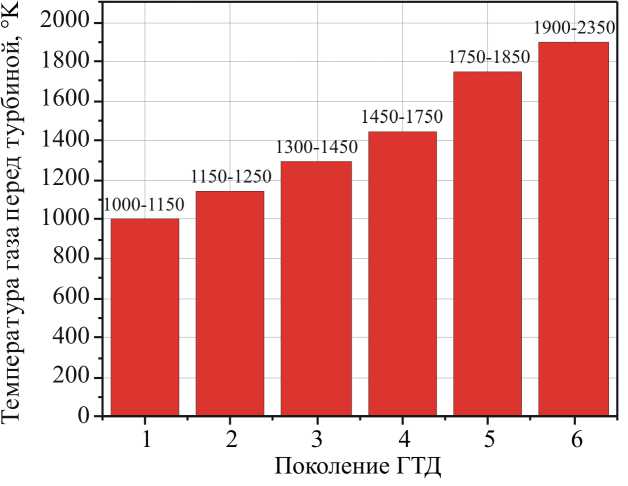
Рис. 1. Температура газа перед турбиной в зависимости от поколения ГТД

Fig. 1. Gas temperature in front of the turbine depending on the generation of gas turbine engines уровне (уровень деталей ГТД) определяются структурно-фазовым состоянием микроструктуры, ее морфологии и свойствами отдельных ее компонентов. На микроскопическом уровне рассматриваемые материалы представляют собой структуру, которая состоит из двух фаз: матрицы из γ-фазы, формирующейся на основе Ni3Al и квазипериодически расположенных дисперсных включений γ'-фазы [2–4] (рис. 2). В изначальном состоянии при нормальных условиях частицы γ'-фазы представляют собой кубоиды со средним размером ~500 нм, разделенные прослойками γ-фазы с поперечным размером 50-90 нм, объемная доля у'-фазы Су составляет порядка 70 % [2; 13].

Различие составов γ- и γ'-фаз обусловливает несоответствие периодов их кристаллических решеток и, как следствие, отличие коэффициентов линейного температурного расширения [1; 2; 14–19]. Относительную разность периодов кристаллической решетки называют мисфитом:

₅ = 2 a - a - , (1) a y + a y'

где a _Y , a _Y , - периоды решеток отдельных фаз.

Наличие мисфита приводит к возникновению характерных для никелевых жаропрочных монокристаллических сплавов межфазных термических напряжений, что делает необходимым его учет в формулировках многоуровневых моделей неупругого деформирования. В работах [15; 20; 21] показано, что мисфит является одним из факторов, влияющих на жаропрочность монокристаллических сплавов.

Для большинства жаропрочных монокристаллических сплавов на никелевой основе характерное значение мисфита δ при температуре 293 K (20 °С) лежит в пре- делах –0,1…–0,2 % [17] и возрастает по абсолютной величине до значений –0,2…–0,4 % при достижении температуры 1173–1273 K (900–1000 °С) [18; 22].

Другим важным параметром является несоответствие упругих модулей отдельных фаз:

m = 2

M у— M y M y + M y'

где M _Y и M _Y , определяются разностью компонент тензоров упругих модулей M = С 1111 - С ₁₁₂₂.

Для большинства современных никелевых монокристаллических сплавов параметр m положителен, его величина имеет порядок 0,1 [23].

Структурно-фазовое состояние никелевых монокристаллических сплавов имеет существенную зависимость от напряженного состояния и температуры [3; 13; 24–26]. Структурно-фазовое состояние можно охарактеризовать двумя основными факторами: объемной долей γ'-фазы и морфологией γ'-включений. При температурах, превосходящих 1223 K (950 °С), резкую тенденцию к уменьшению доли упрочняющей фазы имеет ее зависимость от температуры. На рис. 3 представлена температурная зависимость объемной доли γ'-фазы монокристаллических сплавов SRR99, AM1, CMSX-4. Красной линией показана аппроксимация данных на основе уравнения (3).

Зависимость объемной доли у'-фазы c _Y , от температуры может быть получена на основе эмпирической зависимости [27]

Q

—

c _r= A - Be RT , (3)

где A , B , Q – параметры модели, значения которых для рассматриваемых сплавов представлены в табл. 1, R – универсальная газовая постоянная.

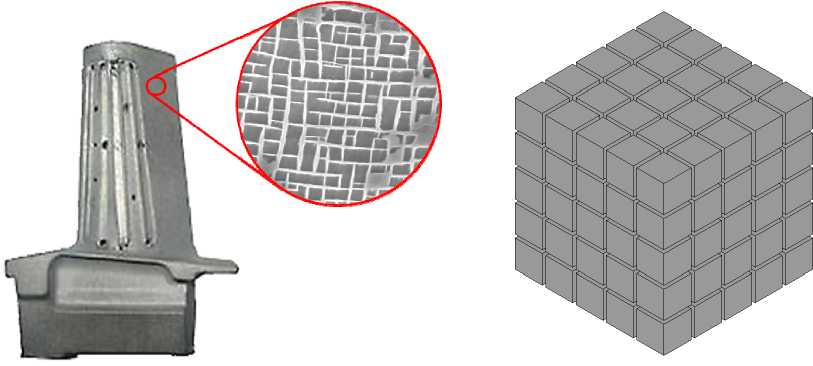
а                                                б

Рис. 2. Микроструктура монокристаллического сплава на никелевой основе [2] ( а ); 3D-идеализация (γ-фаза не показана) ( b )

Fig. 2. Microstructure of a nickel-based single-crystal alloy [2] ( a ); 3D idealization (γ phase not shown) ( b )

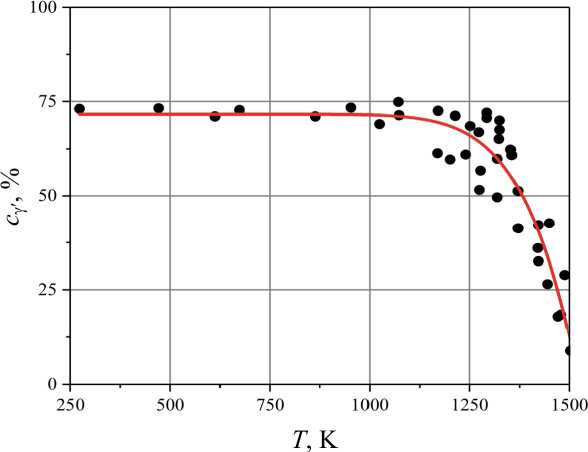
Рис. 3. Зависимость объемной доли γ'-фазы монокристаллических сплавов SRR99, AM1, CMSX-4 от температуры [13]

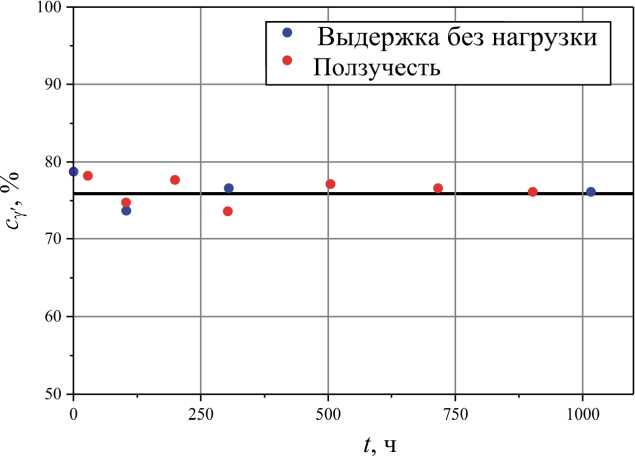
Рис. 4. Зависимость объемной доли γ'-фазы сплава CMSX-4 от времени при изотермической высокотемпературной ползучести при одноосном растяжении и выдержке без нагрузки при T = 1273 K

Fig. 3. Dependence of the volume fraction γ' of the SRR99, AM1, CMSX-4 single-crystal alloys on temperature [13]

Таблица 1/Table 1

Значения параметров уравнения (3)

Values of the equation parameters (3)

Параметр	A , [–]	B , [–]	Q , кДж/моль
Значение	0,71	85071	148

В широком диапазоне температур (вплоть до 1273 K для сплава CMSX-4) для монокристаллических сплавов при изотермической ползучести и выдержках без нагрузки при постоянных температурах объемная доля γ'-фазы остаётся постоянной [23; 28] (рис. 4). При превышении критической температуры доля γ'-фазы имеет тенденцию к уменьшению в процессе ползучести. На рис. 5 представлены зависимости объемной доли γ'-фазы сплава CMSX-4 от времени при высокотемпературной ползучести ( T = 1323 K) при одноосном растя-

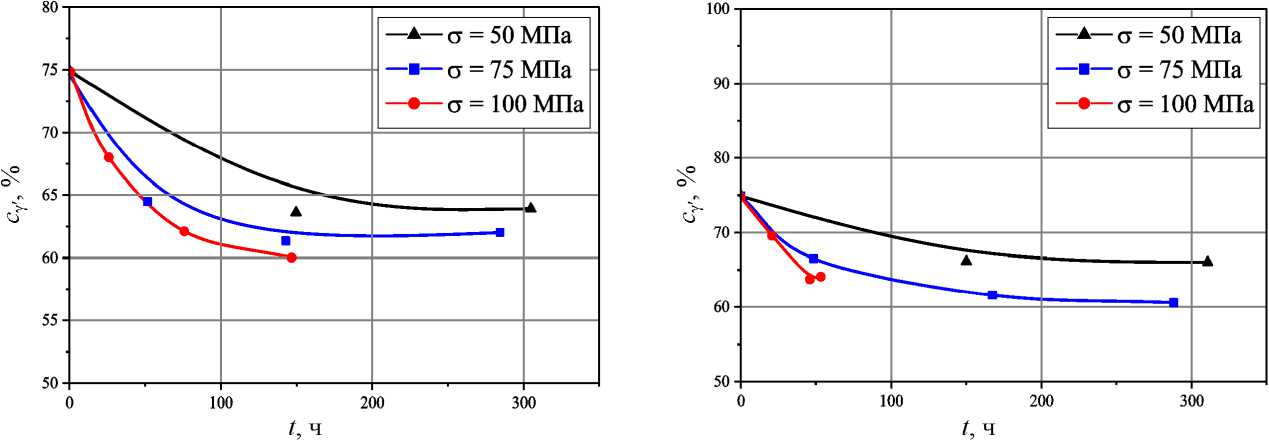
Fig. 4. Time dependence of the volume fraction γ' of the CMSX-4 alloy phase during isothermal high-temperature creep under uniaxial tension and holding without load at T = 1273 K жении в направлении [001] и при сдвиге в плоскости (001) в направлении |^01 1 ], построенные на основе литературных данных [13].

Как было отмечено выше, при высокотемпературной ползучести происходит изменение морфологии γ'. При растяжении вдоль главных кристаллографических осей никелевых монокристаллов изначально кубоидные частицы γ'-фазы вытягиваются в направлении, совпадающим или перпендикулярном приложенной нагрузке, коалесцируют между собой, образуя так называемую рафт-структуру [1–4; 22; 23; 26; 29–31]. В случае, если γ'-частицы сращиваются в стержни или пластины, ориентированные перпендикулярно направлению приложенной нагрузки, говорят о рафтинге N-типа, в противном

b

Рис. 5. Зависимость объемной доли γ'-фазы сплава CMSX-4 от времени при высокотемпературной ползучести ( T = 1323 K) при: а - одноосном растяжении в направлении [001]; b - при сдвиге в плоскости (001) в направлении | 01 1 I

Fig. 5. Dependence of the volume fraction γ' of the CMSX-4 alloy phase at high-temperature creep ( T = 1323 K) with a ) uniaxial tension in the [001] direction and b ) with shear in the (001) plane in the 1 011 ] direction on time

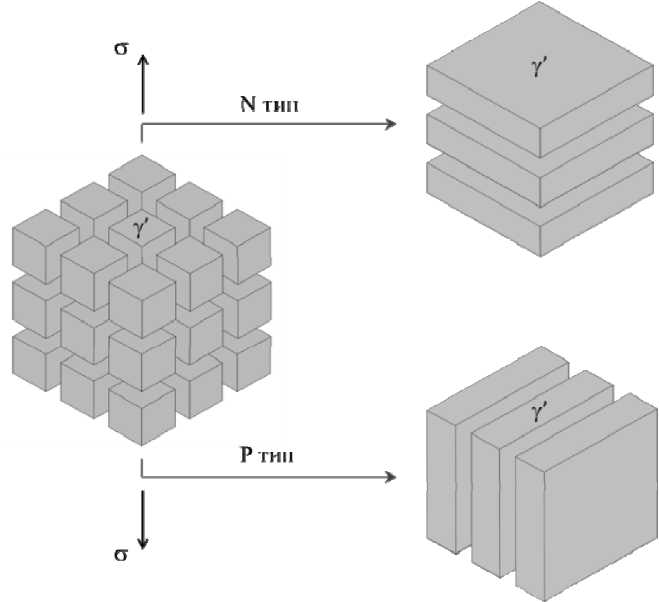
Рис. 6. Схема эволюции микроструктуры монокристаллических сплавов на никелевой основе при высокотемпературной ползучести (рафтинг)

Fig. 6. Scheme of the evolution of the microstructure of nickel-based single-crystal alloys during high-temperature creep (rafting)

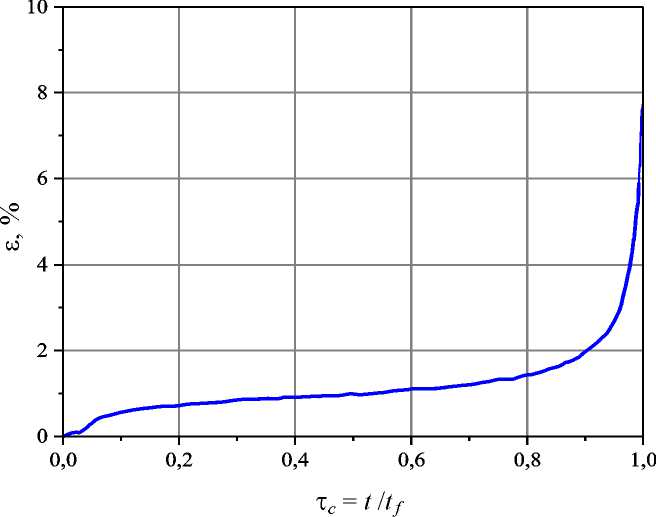
Рис. 7. Кривая ползучести монокристаллического сплава TMS-138 при 1373 K (1100 °С) и 137 МПа [39] для ориентации [001]. По оси абсцисс отложен безразмерный параметр τ _с , равный отношению текущего времени к времени разрушения образца

Fig. 7. Creep curve of the TMS-138 single-crystal alloy at 1373 K (1100 °C) and 137 MPa [39] for the [001] orientation.

The abscissa shows the dimensionless parameter τc, which is equal to the ratio of the current time to the sample destruction time в работе [30], рафтинг имеет существенное влияние на механические свойства сплавов и, как следствие этого, на надежность ответственных элементов ГТД. Рафтинг приводит к снижению жаропрочных свойств сплавов [29], возрастанию скорости ползучести [35]. Рафтинг N-типа способствует снижению сопротивления малоцикловой усталости [36–38].

Эволюция микроструктуры в процессе ползучести (рис. 7) показана на рис. 8 [39] для сплава TMS-138. Рафт-структура образуется на первой, неустановив-шийся стадии ползучести (см. рис. 8, а , b ), на второй стадии морфология γ'-включений практически не меняется, однако толщина γ'-пластин несколько увеличивается, тогда как продольные размеры уменьшаются [17] (см. рис. 8, c ). На третьей, ускоренной стадии ползучести за счет возникновения синусоидальных возмущений на поверхности раздела γ-матрицы и γ'-вклю-чений происходит образование зигзагообразных пластин (рис. 8, d ) вплоть до топологической инверсии микроструктуры (см. рис. 8, e ).

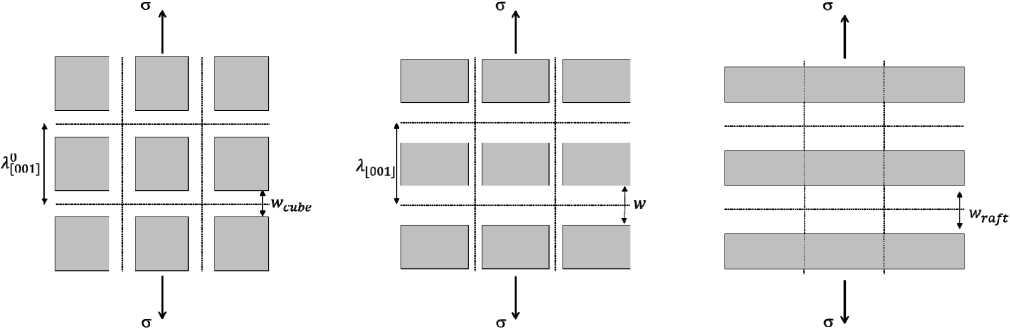
Изменение морфологии γ'-включений при приложении нагрузки вдоль кристаллографических осей монокристалла сопровождается двумя процессами – изменением формы и дальнейшей коалесценцией включений (рафтинг), а также их однородным (изотропным) укрупнением [31]. В этом случае изменение морфологии может описано с помощью двух геометрических параметров – периодом микроструктуры в направлении приложении нагрузки Z [ 001 ] , расстоянием между отдельными включениями в том же направлении w (рис. 9). Удобным представляется использование безразмерного параметра ξ, характеризующего степень рафтинга и определяемого следующим образом:

^= w — wcube raft cube

где w cube – ширина горизонтальных каналов между включениями в исходном материале, w _raf_t – ширина каналов после сращивания включений, 0 < ^ <  1.

Значения w cube и w raft могут быть найдены из следующих соотношений:

wcube = (1  3jCY )^[001р wra/t = (1 — сY' ) ^[001] '

Период микроструктуры в направлении приложении нагрузки Х _[001] независим от уровня нагрузки [31]. Его изменение от температуры может быть определено на основе эмпирической зависимости:

случае речь идет о рафтинге P-типа (рис. 6). Для большинства современных жаропрочных монокристаллических сплавов реализуется рафтинг N-типа. В общем случае тип рафтинга зависит от знаков и величин параметров δ и m , а также от знака приложенной нагрузки.

Изменение морфологии γ'-включений наблюдается, например, при обследовании лопаток газовых турбин после их эксплуатации [19; 22; 32–34]. Как отмечается

^ [001]

^ [001]

f         n -| a

—- It RT J

Степень рафтинга ξ может быть найдена из сле-

дующего соотношения:

^ = 1 - exp

- A 0 exp

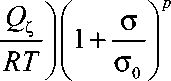
t

а

b                        c                        d                        e

Рис. 8. Эволюция микроструктуры монокристаллического сплава TMS-138 в процессе высокотемпературной ползучести при 1373 K (1100 °С) и 137 МПа [39]: а – τ с = 0,03; b – τ с = 0,1; c – τ с = 0,5; d – τ с = 0,95; e – τ с = 1

Fig. 8. Evolution of the microstructure of the TMS-138 single-crystal alloy during high-temperature creep at 1373 K (1100 °C)

and 137 MPa [39]: а – τ _с = 0.03; b – τ _с = 0.1; c – τ _с = 0.5; d – τ _с = 0.95; e – τ _с = 1

b

Рис. 9. Схема эволюции микроструктуры при высокотемпературной ползучести: а – исходное состояние (ξ = 0); b – промежуточное состояние (0 < ξ < 1); c – образование рафт-структуры (ξ = 1)

Fig. 9. Scheme of microstructure evolution at high temperature creep: а – initial state (ξ=0); b – intermediate state (0 < ξ < 1); c – formation of a raft structure (ξ=1)

Для сплава CMSX-4 параметры моделей (7) и (8) принимают следующие значения [31]: λ _[ ⁰ _001] = 0,709 μm, a = 0,0745, D ₀ = 5,2·10⁹ c^–1, Q _λ = 243 КДж/моль, A ₀ = = 1,16·10¹⁰ c^–1, Q _ξ = 405 КДж/моль, p = 9,83, σ ₀ = 955 МПа.

Наряду с рассмотренными эмпирическими моделями, описывающими процесс эволюции фазового состава, широко представлены термодинамически мотивированные модели [26; 30; 40–42]. Отдельно следует выделить работы, посвященные прямому моделированию процессов эволюции γ/γ'-микроструктуры [43–46].

Турбинные лопатки современных ГТД работают в условиях высокотемпературной ползучести, что делает актуальным разработку соответствующих моделей. Для прогнозирования напряженно-деформированного состояния монокристаллических лопаток при сложных программах термомеханического нагружения можно рассматривать два основных подхода [6; 47–51]:

• •    применение феноменологических моделей ползучести, описывающих поведение материала на макроскопическом уровне [6; 52–56],

• •    применение микромеханических моделей, учитывающих, что неупругие деформации происходят в соот-

• ветствии с механизмом скольжения по активным системам скольжения и в значительной мере зависят от кристаллографической ориентации монокристалла по отношению к направлению внешнего воздействия [1; 6; 52; 57; 58].

На данный момент существует достаточно большое количество микромеханических [1; 6; 47–53; 57–66] и феноменологических [6; 52–56] моделей неупругого деформирования, однако модели, учитывающие наличие γ- и γ'-фаз при высокотемпературной ползучести, находятся на стадии разработки [1; 35; 46; 67].

Целью исследования является разработка многоуровневой микромеханически мотивированной модели ползучести монокристаллических сплавов на никелевой основе, учитывающей наличие γ- и γ'-фаз. Аналогичные исследования для упругопластических моделей рассмотрены в работе [68].

1.    Модели отдельных фаз монокристаллического материала

В монокристаллических материалах неупругие деформации происходят в соответствии с механизмом скольжения по активным системам скольжения и суще- ственно зависят от кристаллографической ориентации монокристалла по отношению к направлению внешнего воздействия.

При использовании микромеханических моделей материала для каждой из фаз учитывалась анизотропия упругих и вязких свойств, особенности кубической сингонии. Предполагалось, что течение в отдельной фазе монокристаллического материала представляет собой результат возможного скольжения в N -системах скольжения, характеризуемых нормалью к а -й плоскости скольжения п ^а и направлением скольжения l ^а ( а = 1,..., N ) .

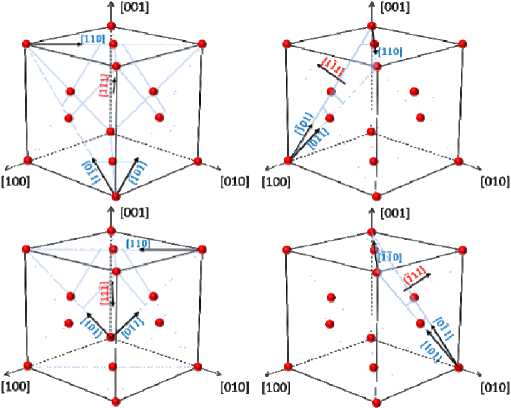
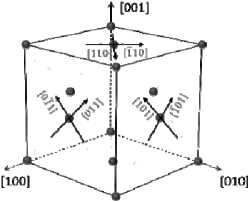
Монокристаллические сплавы с ГЦК решеткой, к которым в том числе относятся и монокристаллические сплавы на никелевой основе, имеют двенадцать октаэдрических систем скольжения вида {111} <011> (рис. 10, а ), шесть кубических систем скольжения вида {001} <011> (рис. 10, b ). Учет двойникования в настоящей работе не производился.

В случае малых деформаций имеем [1; 63–66; 69; 70]:

Е = Еe + £p ,(9)

N

Е p = £ Yа Pa,(10)

а = 1

где тензор Шмида P ^α определяется следующим образом:

Pa = 2(nala + lana ) = (nala)Sym.(11)

В рамках вязкоупругой модели предполагается, что скорость накопления неупругой деформации определяется вкладом всех активных систем скольжения, т.е.

а таких, в которых касательные напряжения т отличны от нуля.

Определяющие уравнения линейно-упругого анизотропного материала имеют вид:

е e = ⁴ С о ,                    (12)

где ⁴ С – тензор упругих податливостей четвертого ранга, в случае кубической симметрии определяемый тремя независимыми константами.

Выбор конкретной формы выражения для скорости неупругих сдвиговых деформаций Y ^а зависит от класса рассматриваемых явлений (пластичность, вязкопластичность, вязкоупругость), а также от особенностей неупругого деформирования рассматриваемого монокристалла.

Множители Y ^а , характеризующие интенсивность неупругого деформирования в а -системе скольжения для вязкоупругой модели, вычисляются на основе уравнений:

• •    модель Нортона для стадии II

Y а= A а|та \stg( (та),(13)

• •    обобщенная модель Нортона (теория упрочнения) для стадии I (неустановившаяся) и II (установившаяся)

Yа= Aа|та Г (уа)m sign (та),(14)

• •    обобщенная модель Нортона (теория течения) для стадии I и II

Y^ = A а|та n^msign (та),(15)

• •    модель Гецова - Кабелевского для стадии I и II

Y^ = A а|та Р (Y^YLrs) msign (та).(16)

где т^а = о P ^а.

а

Рис. 10. Системы скольжения в монокристалле с кубической гранецентрированной решеткой: а – октаэдрические, b – кубические

Fig. 10. Slip systems in a single crystal with a cubic face-centered lattice: а – octahedral, b – cubic

b

В случае одноосного растяжения вдоль направления [001] для заданной истории изменения о - e [00i] ^e [00i] ^CT [₀₀₁][₀₀₁] активными являются 8 эквивалентных друг другу октаэдрических систем скольжения, кубические системы скольжения неактивны. Интегрирование (10) с учетом (9) дает для моделей (13)–(16) следующие выражения для осевых деформаций:

• модель Нортона для стадии II

• обобщенная модель Нортона (теория течения) для стадии I и II

^е [ 111 ][ 111 ]

° [ ¹¹¹ ][ ¹¹¹ ] +    A cube    ( ^ )

E [ 111 ]      ( m cubo ^{+ 1} ) I ³ j

σ n cube [ 111 ][ 111 ]

t m cube ^{+ 1}, (23)

• модель Гецова - Кабелевского для стадии I и II

σ

° [ 001 ][ 001 ]_     ⁸ A_oct

^Ь [ ⁰⁰¹ ][ 0 ⁰¹ ]          с ⁺     n oct +1      [001 ][ 001] ^,

E [ 001 ]       6 2

^е [ 111 ][ 111 ] ^-   _E

+

• обобщенная модель Нортона (теория упрочнения) для стадии I и II

_ °[001][001 ]

^Ь [ 001 ][ 001 ]        р

E [ 001 ]

+ —=

A oct ( ^{1 -} m od )

n oct

о n oct [ 001 ][ 001 ]

V m oct t

, (18)

• обобщенная модель Нортона (теория течения) для стадии I и II

° [ 001 ][ 001 ]_            ⁸ A oct                      +1

^Ь [ 001 ][ 001 ]         E                  noct ^{+ 1}                       [ 001 ][ 001 ]

^{[ 001 ]}       6 ²    ( m _Oct + 1 )

• модель Гецова - Кабелевского для стадии I и II

F. „ , = [ 001 ][ 001 ]

^о [ 001 ][ 001 ] +

^E [ 001 ]

A cube ^{( 1}   m cube )

n cube

n cube

t

1 - m

^ ^{1 -} m cub.

1 (24)

γ revers

^{+ Y} revers

.

+ -;=

A oct ( ¹ - m od ) , °[

n oct ²

n oct

[ 001 ][ 001 ]'

¹ m oct revers

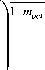
+ Y revers

В случае одноосной деформации вдоль направления [111] для заданной истории изменения о — e [₁₁₁] e [₁₁₁] O' [₁₁₁][₁₁₁] активными являются 12 октаэдрических систем скольжения и 3 эквивалентных друг другу кубические системы скольжения. Вклад кубических систем скольжения, без учета октаэдрических, в осевые деформации определяется следующим образом:

• модель Нортона для стадии II

⁸ [Ш][Ш]

° [ 111 ][ 111 ] ^Е [ш]

4- А

⁺ cUbebe

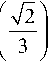
n cube

n cube         ,

' [ 111 ][ 111 ] t

• обобщенная модель Нортона (теория упрочнения) для стадии I и II

_ ° [Ш][Ш] ^fc [ 111 ][ 111 ] -               ⁺

E [ 111 ]

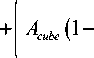
12 m cube )   з

n cube

1 - m _ cube

n cube

° [ 111 ][Ш] t

Уравнения (17)–(24) могут быть использованы для идентификации параметров моделей (13)–(16) для октаэдрических систем скольжения на основе экспериментов по одноосному растяжению монокристаллических сплавов с ГЦК-решеткой вдоль направления [001] (при растяжении вдоль данного направления кубические системы скольжения неактивны). Соответствующие параметры модели для кубических систем скольжения могут быть определены из опытов по одноосному растяжению вдоль направления [111] с использованием уравнений (21)–(24) c учетом ранее найденных констант-моделей для октаэдрических систем скольжения.

2. Представительный объем двухфазного монокристаллического материала

На микроуровне монокристаллические сплавы на никелевой основе представляют собой композит, состоящий из γ-матрицы и квазипериодически расположенных дисперсных включений γ'-фазы (рис. 11). В связи с этим возможно введение представительных объемов (ПО) с различной степенью упрощения реальной ситуации. ПО может вводиться для материалов со статически однородным распределением характеристик при условии сепарабельности масштабов неоднородностей. При выполнении данных условий возможно введение понятия наименьшего объема, который содержит всю статистическую информацию относительно распределения и морфологии неоднородностей материала. В таком случае для любого объема больших размеров его свойства можно получить последовательными переносами или дополнительными реализациями известных статистических характеристик.

В монокристаллических сплавах на никелевой основе частицы γ'-фазы образуют квазипериодическую трехмерную решетку (см. рис. 2). Соответственно, в таком случае в качестве ПО можно рассматривать единичное включение γ'-фазы, окруженное γ-матрицей. Также стоит отметить вклад взаимодействия дислокаций на границе раздела фаз на их взаимное воздействие. Для учета дислокаций на межфазной границе возможно введение дополнительной фазы и соответствующего ей

интерфейсного слоя [71]. Другим распространенным подходом является добавление дополнительных слагаемых в уравнение для касательных напряжений τα [72]. Однако существенным недостатком данных подходов является необходимость большого количества экспериментальных данных, требуемых для идентификации их параметров. В связи с этим в работе принята гипотеза об идеальном контакте между отдельными фазами, предложенная в работe [73]. Достоверность применяемых моделей и гипотез подтверждается результатами экспериментальной верификации. Конечно-элементная (КЭ) модель одного из простейших вариантов ПО представлена на рис. 11. На рис. 12 показаны представительные объемы с различными долями γ'-фазы, используемые в дальнейшем. КЭ-модели ПО для разных степеней рафтинга ξ представлены на рис. 13.

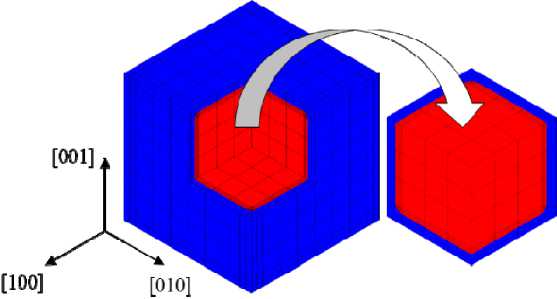
Рис. 11. Конечно-элементная модель ПО γ / γ'-микроструктуры монокристаллического сплава на никелевой основе (объемная доля γ'-фазы 70 %, ξ = 0). Справа на рисунке изображен фрагмент ПО соответствующий его 1/8 части

Fig. 11. Finite element model of the representative volume γ / γ' of the microstructure of a nickel-based single-crystal alloy (volume fraction of the γ' phase is 70 %, ξ = 0). On the right in the figure, a representative volume fragment corresponding to its 1/8 part is shown

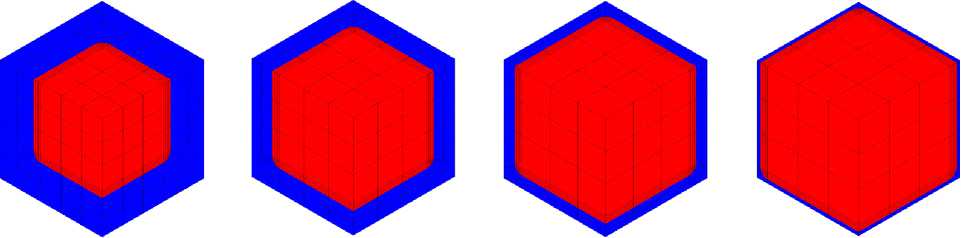
30 %                    50 %                    70 %                    90 %

Рис. 12. Конечно-элементные модели ПО γ / γ'-микроструктуры монокристаллического сплава на никелевой основе с разной объемной долей γ'-фазы, ξ = 0 (показана 1/8 часть ПО)

Fig. 12. Finite element models of the representative volume of the γ / γ' of the microstructure of a nickel-based single-crystal alloy with different volume fractions of the γ' phase, ξ = 0 (1/8 of the representative volume is shown)

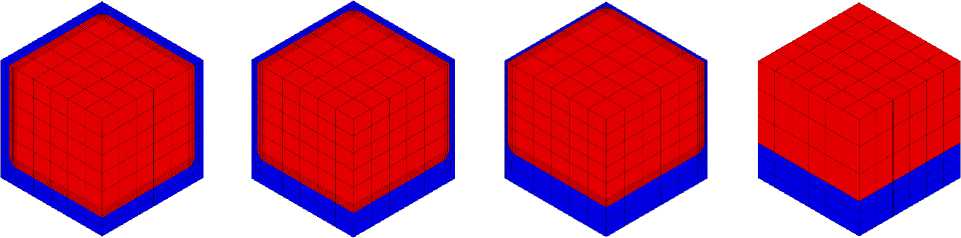
ξ = 0,25                        ξ = 0,5                        ξ = 0,75                         ξ = 1

Рис. 13. Конечно-элементные модели ПО γ / γ'-микроструктуры монокристаллического сплава на никелевой основе для разных степеней рафтинга ξ, объемная доля γ'-фазы 70 % (показана 1/8 часть ПО)

Fig. 13. Finite element models of the representative volume of the γ / γ' of the microstructure of a nickel-based single-crystal alloy for different degrees of rafting ξ, the volume fraction of the γ' phase is 70 % (1/8 of the representative volume is shown)

3.    Определение эффективных свойств двухфазного монокристаллического материала 3.1.    Конечно-элементная гомогенизация

Определение эффективных свойств монокристаллических сплавов с различной долей γ'-фазы и разными степенями рафтинга ξ осуществлялось при помощи метода КЭ гомогенизации. При проведении расчетов использовались определяющие уравнения нелинейно вязкоупругого материала (9)–(16).

Нелинейные краевые задачи решались в трехмерной квазистатической постановке. В основе применяемого в расчетах КЭ программного комплекса PANTOCRATOR [75] используется уравнение виртуальных работ:

J с • 8 dV = J f V • 8 u dV + J f S • 8 u dS ,     (25)

• V               V                S „

где 8 г = ( V8 u ) S , f _V и f _S – заданные объемные и поверхностные силы. Следствием (25) могут быть получены уравнения равновесия V • с + f V = 0 в объеме и силовые граничные условия П • с| _s = f S . Для исключения твердотельных движений необходимо задание кинематических граничных условий.

Рассматриваемые краевые задачи КЭ-гомогени-зации для представительного объема в форме куба (рис. 11) решались со статическими граничными условиями (на трех некомпланарных гранях) и условиями симметрии на остальных трех гранях ПО:

n • с| = n • с * ,                     (26)

S о

U S = 0.                    (27)

Условие (26) обеспечивает выполнение условия эргодичности с •• £ = с • • £ , что гарантирует существование и единственность решения соответствующих краевых задач, а также равенство энергий при деформировании гомогенизированного и гетерогенного материала ПО. Выбор данного типа граничных условий обусловлен простотой их реализации для задач ползучести, подразумевающий приложение силовых граничных условий. Использование других типов граничных условий, например условий периодичности, приводит к значительным трудностям при их программной реализации. При решении задач гомогенизации нагрузка прикладывалась вдоль кристаллографического направления [001].

Для определения гомогенизированного напряженно-деформированного состояния использовались ос-редненные по представительному объему значения тензоров деформаций и напряжений, полученные в КЭ-решении:

г =--- [ £ dV ,               (28)

VПО ∫VПО с =---[ с dV .               (29)

^VПО ^{∫ VПО}

Используемые в расчетах упругие характеристики γ- и γ'-фаз для случая кубической симметрии приведены ниже в табл. 2. Параметры обобщенной модели Нортона в форме теории упрочнения представлены в табл. 3.

Таблица 2/Table 2

Упругие характеристики γ- и γ'-фаз [66]

Параметр	γ-фаза	γ'-фаза
Е [001] , ГПа	84,3	95,1
^ [00Ц[0101, [-]	0,4	0,4
G [0011[0101 , ГПа	96,67	100,11

Таблица 3/Table 3

Параметры модели ползучести (14) γ- и γ'-фаз [2]

	γ-фаза	γ'-фаза
A , (MПa) –n	1,99∙10 –41	0,61∙10 –51
n , [–]	4,24	5,36
m , [–]	0	0

Решение нелинейных краевых задач ползучести ПО гетерогенной структуры получено на основе инкрементально-итерационных процедур с использованием КЭ программного комплекса PANTOCRATOR [75], обладающего возможностью получения КЭ-решения краевых задач с использованием микроструктурных упругопластических, вязкоупругих и упруговязкопластических моделей деформирования материала, а также встроенными средствами процедуры гомогенизации гетерогенных сред.

Реализуемый подход основан на предположении, что механические свойства жаропрочных монокристаллических сплавов на макроуровне полностью определяются структурно-фазовым состоянием его микроструктуры и могут быть определены методом конечно-элементной гомогенизации. Это позволяет сформулировать феноменологические модели ползучести на макроуровне, которые учитывают изменение объемных долей отдельных фаз и их морфологии.

Верификация предложенного подхода осуществлялась путем сравнения результатов КЭ-гомогенизации с экспериментальными кривыми ползучести сплава ЖС-32 [76] на макроуровне. Сравнение проведено для сплава в исходном состоянии и после старения при 1323 K (1050 oC) в течение 1500 ч. Объемная доля γ'-фазы составляет 70 % для материала в исходном состоянии и 58 % после старения. Сравнение кривых ползучести, полученных при температуре 1323 K (1050 oC), нагрузке 150 МПа, приложенной вдоль кристаллографического направления [001], c результатами КЭ-гомогенизации представлено на рис. 14. Наблюдается удовлетворительное соответствие результатов расчета экспериментальным данным в широком диапазоне времен выдержки под нагрузкой.

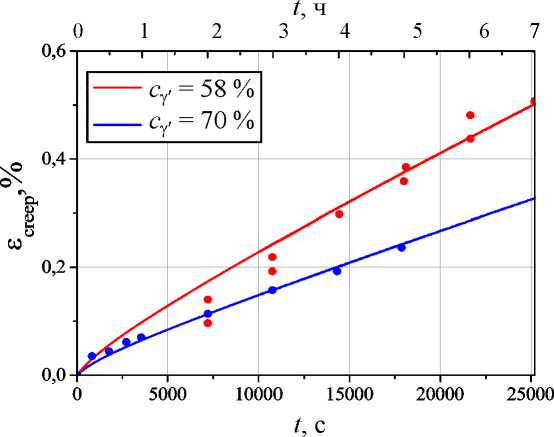
Рис. 14. Сравнение результатов КЭ гомогенизации с экспериментом

Fig. 14. Comparison of the results of FE homogenization with experiment

На основе предложенной модели были построены кривые ползучести для монокристаллических сплавов на никелевой основе для разных объемных долей γ'-фазы (см. рис. 12) для аналогичных экспериментальным значениями нагрузки и температуры. Полученные результаты представлены на рис. 15. Установлено, что скорость ползучести возрастает с уменьшением объемной доли γ'-фазы.

Анализ зависимости скорости установившейся ползучести от объемной доли γ'-фазы позволяет сформулировать феноменологическую модель ползучести монокристаллических сплавов на никелевой основе, учитывающую соотношения между объемными долями отдельных фаз:

6 СГ0Р [001] ( c , ' ) = C ( De - c ’ E - 1 ) ,           (30)

где C , D , E – параметры модели, в общем случае зависящие от температуры и прикладываемой нагрузки. Данные параметры определяем на основе вычислительных экспериментов. В рассматриваемом случае данные параметры принимают следующие значения: С = 6,75·10^–8 c^–1, D = 19,37, E = 0,026. Результаты аппроксимации на основе модели (30) показаны красной линией на рис. 15, b .

Для оценки влияния морфологии γ'-включений были проанализированы результаты гомогенизации для сплавов с различной степенью рафтинга (см. рис. 13) при постоянном значении доли γ'-фазы, равном 70 %. Результаты моделирования представлены на рис. 16.

Дальнейший учет влияния степени рафтинга на скорость ползучести может производиться на основе простейшей феноменологической модели:

£S [001^ ) = F G + G ) . (31)

где F, G – параметры модели, в общем случае зависящие от температуры и прикладываемой нагрузки, определяемые основе вычислительных экспериментов и принимающие в рассматриваемом случае значения: F = 1,32·10^–8 c^–1, G = 8,4. Результаты аппроксимации на основе модели (31) показаны красной линией на рис. 16, b .

Феноменологические модели (30), (31) могут быть обобщены на многоосный случай по аналогии с уравнениями (10), (13):

Nn

£ ^p = £ C ( De" c ^y '^e - 1 )|т ^а| ⁿ sign (т^а) Р ^а, (32) а = 1

Nn

£ ^p = Z F ( ^ + G )| t“| n sign (т^а) Р ^а- (33) а = 1

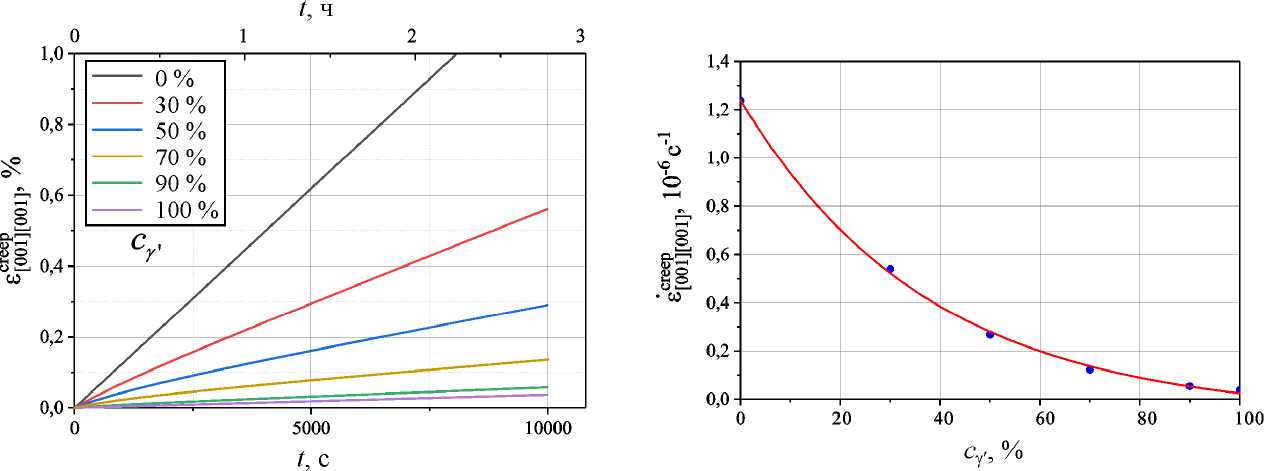
b

Рис. 15. Результаты КЭ-гомогенизации для ПО с разными долями γ'-фазы, ξ = 0: а – кривые ползучести; b – зависимость скорости ползучести от объемной доли γ'-фазы. Точками показаны результаты, полученные при помощи КЭ-гомогенизации, результаты аппроксимации на основе модели (30) показаны красной линией

Fig. 15. Results of FE homogenization for the representative volume with different fractions of the γ' phase, ξ = 0: а – creep curves, b – dependence of the creep rate onthe volume fraction of the γ' phase. The dots show the results obtained using FE homogenization, the results of approximation based on model (30) are shown by the red line

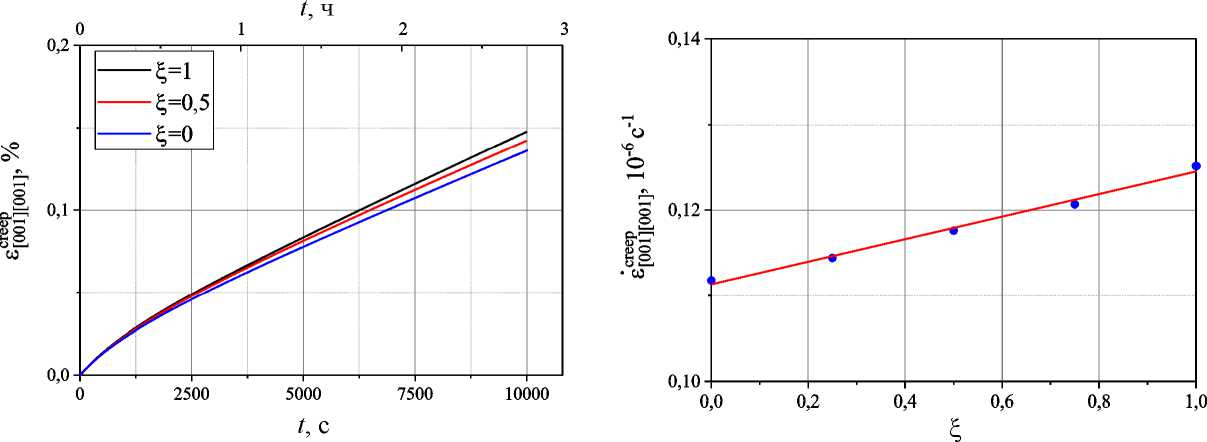
b

Рис. 16. Результаты КЭ-гомогенизации для ПО различной степенью рафтинга: а – кривые ползучести; b – зависимость скорости ползучести от степени рафтинга ξ. Точками показаны результаты, полученные при помощи КЭ-гомогенизации, результаты аппроксимации на основе модели (30) показаны красной линией. c _Y ‘ = 70 %

Fig. 16. Results of FE homogenization for the representative volume with different degrees of rafting: а – creep curves; b – dependence of the creep rate on the degree of rafting ξ. The dots show the results obtained using FE homogenization, the results of approximation based on model (30) are shown with the red line. c _Y ‘ = 70 %

На основе уравнений (32) и (33) в предположении, что параметр C в (32) зависит от £ , а D и E не зависят, предлагается комбинированная модель нелинейной вяз-ко-упругости с одновременным учетом рафтинга и концентрации у-фазы:

Nn

Ё p = £ H ( 1 - De"^{c y} ' ^e ) ( ^ + G )| т ^а|" sign ( т ^а ) P ^a . (34) a=1

Результаты моделирования позволяют заключить, что рафтинг оказывает существенно меньшее влияние на скорость ползучести, нежели изменение объемной доли γ'. Так скорость ползучести материала со степенью рафтинга ξ = 1 увеличивается на 11 % по сравнению с исходным материалом. В то же время уменьшение объемной доли на 12 %, соответствующее ξ = 1 [76], приводит к более чем двухкратному росту скорости ползучести (см. рис. 15, 16). В связи с этим, так как учет рафтинга требует проведения дополнительных вычислительных экспериментов, при исследовании вязкоупругих свойств монокристаллических сплавов на никелевой основе изменением морфологии γ'-включений можно пренебречь по сравнению с изменением объемной доли γ'-фазы.

• 3.2.    Реологические (структурные) модели монокристаллического материала

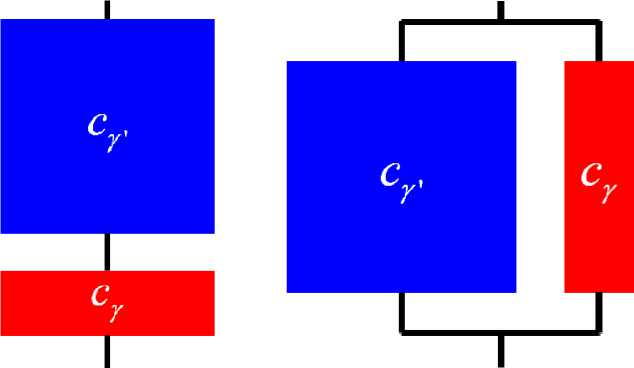
Эффективные свойства гетерогенных материалов могут быть определены не только на основе метода КЭ-гомогенизации, но и при помощи аналитических оценок на основе реологических (структурных) моделей [77–79]. Простейшие оценки могут быть получены при использовании подходов Рейсса [80] (последовательное соединение элементов) и Фойгта [81] (параллельное

а                                  b

Рис. 17. Реологические (структурные) модели монокристаллических сплавов на никелевой основе: а – модель Рейсса; b – модель Фойгта

Fig. 17. Rheological (structural) models of nickel-based single-crystal alloys: а – Reuss model, b – Voigt model соединение элементов) (рис. 17). Каждый из реологических (структурных) элементов для γ- или γ'-фазы является вязкоупругим.

Модель Рейсса (см. рис. 17, а ) приводит к следующему выражению для скоростей деформации:

Ё = СyЁy + Cy,Ёy■.(35)

Напряжения в отдельных структурных элементах принимаются равными между собой:

oy = Оy■.(36)

Скорость неупругих деформаций определяется следующим образом [70; 82]:

W y

ё p=cyz y; pa+c,‘Z y"■ p".(37)

a=1

где c _Y , c _Y ‘ - объемные доли у- и у'-фазы соответственно ( c _Y + c _Y ‘ = 1), n _y и n _r - число систем скольжения в структурных элементах, соответствующих γ- и γ'-фазе соответственно. В данной работе фазовые переходы не рассматриваются, в связи с этим c _Y , является константой.

Интегрирование (37) c учетом (35), (14) и (12) дает следующее выражение для полных деформаций:

е,

^ [ 001 ][ 001 ]

• [ 001 ][ 001 ]         р

^E Re us

+

' Y

⁺ c Y'

где E Reus[001] =

n Y

^ [ 001 ][ 001 ]'

n Y

t

1- m y

AY' (1   mY' ) ^[001][001]t nY'

I 6 2 J

^E Y[001] ^E y '[001]

с y ^E Y '[001] ⁺ с y ' ^E Y[001]

Модель Фойгта (параллельное соединение структурных элементов, рис. 17, b ) приводит к следующему выражению для тензора напряжений:

О = c Y О Y + c Y' O Y' .

Данная модель также подразумевает равенство деформаций в отдельных структурных элементах:

£ y = £ y ' -                         ⁽⁴⁰⁾

Ввиду трансцендентности уравнений, получаемых следствием подстановки (39) в (14) относительно напряжений в отдельных структурных элементах, их значения не могут быть определены аналитически и выражены через деформацию явным образом. В связи с этим решение данных уравнений было выполнено численно, при помощи метода Ньютона.

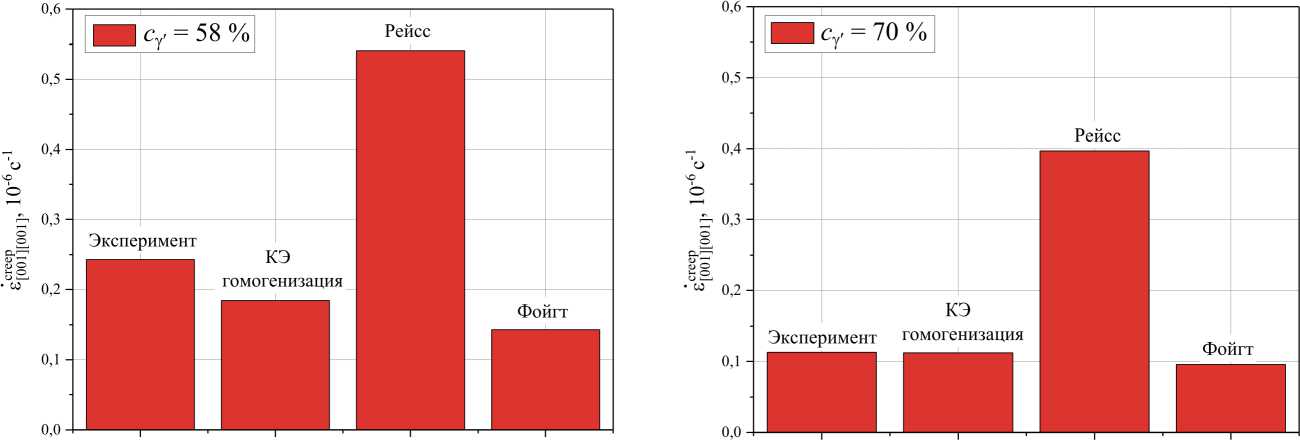
Сравнение скоростей деформаций на установившейся стадии ползучести, полученных при помощи различных реологических моделей, с результатами КЭ гомогенизации и экспериментальными данными представлено на рис. 18. Наилучшее совпадение демонстрируют результаты КЭ-гомогенизации, удовлетворительное совпадение показывает модель Фойгта (39). Наихудшее совпадение демонстрирует модель Рейсса (35), (38).

Заключение

Предложены микромеханически мотивированные подходы, позволяющие предсказать поведение двухфазных монокристаллических сплавов на никелевой основе при высокотемпературных механических воздействиях с учетом наличия микроструктуры. Рассмотрены два альтернативных подхода для анализа неупругого поведения: (i) численный на основе метода конечно-элементной гомогенизации для двухуровневой модели двухфазного монокристаллического материала с учетом изменения γ–γ'-микроструктуры сплава, и (ii) аналитические оценки, используемые в механике композитов, получаемые в предположении равенства напряжений или деформаций в отдельных фазах.

На основе экспериментальных кривых ползучести для сплава ЖС32 проведена верификация предложенных моделей. Выяснено, что наилучшее соответствие дает метод конечно-элементной гомогенизации, несколько

а                                                         b

Рис. 18. Сравнение скоростей установившейся ползучести, полученных с помощью различных подходов, с экспериментальными данными по одноосному растяжению сплава ЖС32 [76] (σ [₀₀₁][₀₀₁] = 150 МПа) с разными значениями объемной доли γ': а – с γ' = 58 %; b – с γ' = 70 %

Fig. 18. Comparison of steady-state creep rates obtained using different approaches with experimental data on uniaxial tension of the ZhS32 alloy [76] (σ [₀₀₁][₀₀₁] =150 MPa) with different values of the volume fraction γ': а – c _γ' = 58 %, b – c _γ' =70%

худшее соответствие демонстрируют аналитические оценки с использованием структурных моделей, основанных на подходе Фойгта. Аналитическая оценка по Рейссу продемонстрировала наибольшее расхождение с экспериментальными данными.

Установлено, что наиболее существенный вклад в изменение скорости ползучести вносит изменение объемной доли γ'-фазы: так, при изменении объемной доли с 70 до 58 % скорость ползучести на установившейся стадии возрастает более чем в два раза. Изменение морфологии γ'-включений имеют меньшее, по сравнению с изменением объемной доли γ'-фазы, влияние на