Моделирование процессов тепло- (массо-) переноса в микроканалах при чип-реализации электрофореза

Традиционно при решении задач проектирования прибора или разработки новой методики анализа математическое моделирование базовых процессов или явлений применяется как вспомогательная стадия работы. Тем самым результаты, достигнутые на стадии математического моделирования, крайне редко непосредственно проявляются в конечном результате. В частности, среди публикаций, касающихся разработки микрофлюидной аналитической системы, проводимой в Лаборатории информационно-измерительных био-и хемосенсорных микросистем Института аналитического приборостроения РАН [1-14], лишь меньшая их часть [3, 6, 12-14] достаточно подробно рассматривает постановку задач математического моделирования и используемые методы решения.

В контексте проводимых лабораторией работ основной задачей моделирования является исследование различных способов управления процессами анализа (разделения) смесей в каналах микрочипа при реализации электрофореза. Таким образом, главное внимание уделялось проверке эффективности традиционных и новых методов управления микропотоками вещества, выбору управляющих параметров/характеристик как конструктивных элементов системы, так и объектов анализа, а также поиску возможных оптимальных режимов.

Как правило, критерием оптимизации был максимум разрешения аналитических пиков компонент, и сама процедура решения также была хорошо известна в силу очевидной математической формализации задачи — поиск условного экстремума функции нескольких переменных при ограничениях в форме неравенств.

Следует выделить ограничения различной при- роды (происхождения):

• — ограничения, связанные с практическим проведением анализа (ограничение на максимальное время анализа, с чем могут быть связаны ограничение сверху длины микроканала и ограничение снизу величины управляющего продольного электрического поля);

• —    ограничение, связанное с тепловым действием электрического поля (ограничение сверху на величину тепловой мощности);

• —    ограничение, связанное с чувствительностью детектора (ограничение снизу на объем пробы или/и количество продукта реакции, если таковая осуществляется в микроканале);

• —    конструктивно-технологические ограничения по выбору размеров микроканала (ширина, соотношение глубины и ширины, угол наклона стенок и т.д.), связанные с уровнем развития технологии;

— финансово-экономические ограничения, не позволяющие принимать дорогостоящие решения (усложнение формы канала — переменность профиля, множественность изгибов и смешиваний, использование крайне сложных алгоритмов управления электрическими и тепловыми полями, что приведет к резкому удорожанию программноматематического обеспечения (ПМО), применение сверхдорогих реагентов при проведении химической реакции и т.п.).

Таким образом, практическая задача моделирования — поиск условно оптимальных конструктивных решений и режимов анализа для микро-флюидной аналитической системы при чип-реализации электрофореза.

БАЗОВЫЕ ПОЛОЖЕНИЯ

Основные базовые положения, в соответствии с которыми осуществляется построение математических моделей процессов конвективно-диффузионного массопереноса в микроканалах чипа, достаточно традиционны. Среди признанных положений: 1) гипотеза сплошной среды, приемлемая для всех объектов, кроме самых крупных (например, клеток); 2) общая схема процесса — длинный тонкий канал прямоугольного или тра-пециидального сечения и короткая "пробка" анализируемой смеси; 3) система уравнений неразрывности и Навье—Стокса для описания распределения концентраций компонент; 4) система уравнений Пуассона—Больцмана для моделирования электрического потенциала, температурного поля и конвективного скоростного профиля.

Следует подчеркнуть, что распределение конвективной скорости по сечению канала в общем случае может отличаться от параболического, поскольку величины, входящие в соответствующее уравнение системы Пуассона—Больцмана (параметры канала, концентрация и вязкость буфера, температура и т. д.) могут быть различны.

Кроме того, одним из базовых положений, определяющим выбор метода решения, является отказ от получения точных численных решений (нестационарное пространственное распределение концентраций компонент) и использование интегральных характеристик (аналитических пиков). Такой подход допустим, поскольку детектор осуществляет суммирование откликов (по существу, концентраций) по всей глубине микроканала и иногда и по его ширине. Таким образом, анализируемыми характеристиками массопереноса будут параметры (центр тяжести, дисперсия, коэффициент асимметрии и т.д.) аналитических пиков компонент.

СПОСОБЫ УПРАВЛЕНИЯ АНАЛИЗОМ

Более подробно пять основных способов управления микропотоками вещества рассмотрены в работе [13], поэтому следует ограничиться их перечислением: 1) выбор топологии (геометрии) микроканала; 2) подбор управляющих напряжений для задания продольного (аксиального) электрического поля; 3) введение микрореактора с последующей регистрацией продукта; 4) управление состоянием поверхности микроканала и 5) создание управляемого температурного поля. Далее будут проиллюстрированы основные результаты моделирования указанных способов управления микроанализом при чип-реализации электрофореза.

Выбор топологии (геометрии) микроканала

В рамках указанного способа управления рассматривается оптимизация конструкции только для простейших топологий, а именно простой и двойной крест с варьированием ширины канала и длины пробки анализируемого вещества. Поскольку типичными размерами микроканала и пробы являются: длина L = 1-3 см, ширина 2h от 60 до 100 мкм, глубина b от 10 до 20 мкм (но не более полуширины), а объему пробы V от 50 до 300 пл соответствует длина пробки А от 80 до 500 мкм, очевидно, что базовая схема движения короткой пробки в длинном тонком канале подтверждается.

В первом приближении микроканал интерпретировался совокупностью плоских щелей. Параметры аналитического пика для базовой 2D-mo- дели плоской щели вычислялись на основе метода моментов [6, 12]. Было показано [15, 16], что дифференциальное уравнение нестационарного пространственного распределения концентраций компоненты смеси (уравнение Навье—Стокса) может быть преобразовано для моментов к форме

∂ µ _n ∂ t

-

_ *

D ■

^{д 2} В п

d z^г

• —    nu * (1 - z m ) ц _{п ч} + п ( п - 1) D * Ц п - 2 ; ⁽¹⁾ п — 0,1,2,3,...

где u ^* , D ^* — это нормированные на полуширину микроканала максимальная скорость конвективного движения и коэффициент диффузии соответственно; z — относительная ширина канала, отсчитываемая от оси [6].

Граничные условия для моментов любого порядка являются условиями второго рода, связанными с непроницаемостью стенки канала и осевой симметрией:

^дЦ п ^(0, t ) а ^дЦ п ^(1, t ) А ---------— о, ---------— о.

∂ z            ∂ z

Начальные условия определяются исходным распределением вещества, которое мы полагаем соответствующим пробке относительной длины 2 А с равномерным распределением вещества по сечению. Решение предполагает разложение конвективного скоростного профиля в ряд Фурье четным образом, т. е. вычисление коэффициентов B :

• 1    - | z| ^m — B ⁰ + ^ B^J cos( n jz ). Отметим, что j — 1

гипотеза о параболическом конвективном профиле была отвергнута в пользу более общей гипотезы — профиля с параметром клиновидности т. Тогда

^(z, t) = u" B 01 + У j—1

u * BJ

D ЧП ) ²

cos( n jz ) ,

и его среднее значение (среднее по сечению мик- роканала положение центра тяжести пика) есть u*B0t, где B0 = т/(т+1).

Средняя дисперсия пика есть

. . f          +^ D ^{j 2}

( a ²) = 2 + Pe²Y---

V    нШ

f A2

V

+

/

D * t +

B j )

+^ ³ Pe²V 2    £ ( n j )

/

,

где число Пекле определяется как Pe = u/D*. Выражение (2) аналогично так называемой Тейлоровской дисперсии. Очевидно, что если максимальная скорость и коэффициент диффузии являются ха-

рактеристиками анализируемого вещества, то уп-

равление положением центра тяжести и дисперсией пика осуществляется 3 параметрами: полушириной h (влияет на u , D ), объемом пробы (длина пробки А ) и параметром клиновидности профиля m (последнее регулируется с помощью других методов управления).

На основе базовой модели плоской щели были

решены некоторые сопровождающие задачи: канал трапециидального сечения был отмоделирован как совокупность плоских слоев разной ширины, а также проведено моделирование застойных зон (пристеночного обедненного веществом слоя) в соответствии с моделью неравномерной загрузки пробки [6]. Последние модели не подтверждаются экспериментами, поскольку выравнивание количества вещества по сечениям канала должно происходить, согласно расчетам, в течение нескольких секунд. Кроме того, эксперименты не подтверждают неравномерность загрузки. Таким образом, моделирование застойных зон должно осуществляться при воображаемой полупроницаемой стенке. Переход к трехмерной задаче как совокупности плоских щелей приводит к заниженным оценкам дисперсии, поскольку модель плоской щели не учитывает массообмен между слоями.

Расчет управляющих потенциалов (продольного электрического поля)

На основе системы уравнений Кирхгофа и Ома ранее были выполнены [3] расчеты схемы управляющих потенциалов (топология: крест и двойной крест) с учетом нестационарности баланса потенциалов из-за изменения удельного сопротивления микроканала при движении смеси. При этом каналы рассматривались как делители напряжений. Исследовались два режима: ввод пробы и собственно анализ (разделение компонент). Для указанных двух режимов требовалось решить задачу оптимизации по критерию: минимум "ухода" вещества в боковые каналы при минимуме необходимых переключений управляющих потенциалов.

Основной принцип подбора потенциалов — минимизация "засасывания" буфера в пробу и "рассасывания" пробы в боковые каналы — обеспечивается подачей блокирующих потенциалов, примерно равных потенциалам в узлах (точках пересечения каналов). В расчетах было учтено переменное сечение микроканала вблизи от управляющих электродов. Была предложена удачная геометрическая аппроксимация переменного сечения канала, на основе которой были оценены параметры делителя напряжений. Подробный расчет геометрии каналов и баланса потенциалов также представлен в [3]. Так, при напряжении управляющих потенциалов для анализа U 1 = 0, U ₂ = = 1500 B экспериментально найденные величины запирающих потенциалов будут     U 3 =

= 5 B, U ₄ = 25 B; их расчетные значения [3] оказались соответственно U 3 = 7.5 В и U ₄ = 29.7 B. Полученные оценки имели расхождение с экспериментально найденным оптимальным режимом управления не более 5 В.

Введение микрореактора

Основаниями предполагать эффективным введение микрореактора для последующей регистрации продукта можно считать: а) большую чувствительность детектирования к продукту, а не исходному реагенту; б) иные по сравнению с реагентом конвективные скорости и коэффициенты диффузии, что может способствовать изменению параметров пика.

Базовое уравнение Навье—Стокса для реагента и продукта реакции преобразовано с учетом химической реакции 1-го порядка. Очевидно, что указанное уравнение дополнительно содержит константу скорости химической реакции к , которая может быть управляющим параметром процесса анализа. Данную модификацию изначально предложил В.П. Андреев [17], использовав следующие допущения: 1) капилляр — круглый, субмиллиметрового диаметра; 2) профиль — конвективный, по скорости — параболический; 3) равенство конвективных скоростей продукта и реагента. Эти допущения неприемлемы в нашем случае, хотя сам предложенный подход позволил модифицировать уравнение (1) к уравнению моментов реагента и продукта.

Эти дифференциальные уравнения для реагента и продукта принимают вид соответственно

дц П - D д2 ц n = dt      1 dz2

= nu i (1 - z m ¹ ) ц П - I + n ( n - 1) D i ц П - ₂ - k u П ,

-ц - D d^L= dt      2 dz2

= ⁿu 2 (1 ^- | z | ² ) ^ 2 - 1 + n ⁽ n ^- 1) D 2 ^ 2 — 2 + R ll П .

Здесь верхние индексы 1 соответствуют характеристикам реагента, 2 — продукта реакции первого порядка.

Граничными условиями являются условия второго рода; начальные условия соответствуют случаю равномерно заполненной "пробки" реагента относительной длины А и отсутствию продукта реакции. Видно, что первое уравнение в системе

• 1        ..1 „- kt

• (3)    заменой момента ^ц _п ^ ^ц _п • e позволяет получить уравнение для "амплитуд" моментов реагента с решением, соответствующим отсутствию реакционного члена, т. е. уравнению (1).

Здесь подставлены нормированные скорости ( u i ), коэффициенты диффузии ( D i ) и параметры клиновидности ( m_i ). Момент нулевого порядка (количество вещества) для реагента имеет вид ц 1 = exp( - kt ), а для продукта реакции — ц 2 = 1 - exp( - kt ) • Так как необходимое для детектирования количество продукта ограничено снизу, то произведение kt также должно быть ограничено снизу.

Средние по сечению положения центров тяжести пиков реагента и продукта определяются соответственно как

C ¹ = и 1 B 1 1 и

• _C 2 ₌

= t ( и ₂ B 0 - и 1 B ¹ • exp( - kt )) /(1 - exp( - kt )) -

• - ( и ₂ B ₀ ² - и 1 B 1 )/ k .

Коэффициенты разложений конвективных профилей реагента и продукта реакции в ряды Фурье по косинусам B i ( i = 1,2) могут быть различны. В случае совпадения конвективных профилей (то есть u 1 = u 2 и m 1 = m 2 ) будет равенство центров тяжести пиков реагента и продукта.

Выражение для средней дисперсии пика продукта реакции вычисляется по аналогии с теорией вероятностей:

• < о ² >=< ц 2 ² >  / ц 0 - ( < ( ц 2 )² >  /( ц 0 ²)² ) •

То есть требуется вычисление среднего момента второго порядка и среднего квадрата момента первого порядка. Поскольку уравнения решались методом разложения по собственным функциям соответствующей однородной задачи Штурма— Лиувилля, то момент первого порядка представлял-

иувилля, то момент первого порядка представлялся в форме ц 2 (z, t) = W0 (t) + ^ Wj (t) cos(nz), а среднее значение квадрата этого момента будет

W 0 ²( t ) + 1 ^ j t )•

2 _j

Построение последовательности функций W j ( t ) проводится по схеме:

• а)    W ₀( t ) = C ²(1 - exp( - kt ));

• б)    построение функций W j производится с введением вспомогательных коэффициентов:

если k ^ D₂ n ² j ², то

W j ( t ) = y exp ( - D 2 ^{n 2} j² t ) + -^П^⁺

+ a exp ( - kt ) + в exp ( - ( k + D 1 n ² j ²) t ) ,

при этом

a =

k

u ₁ B ¹ _j

D 1 n ² j j

-

u ₂ B ² _j

в =

Y =

-

-

D 2 П ² jj

ku ₁ B ¹ _j

-

k

,

D 1 n ² j ² ( D 2

u ₂ B ² _j

D2n2j2

-

-

D 1 ) n ² j j

a - в ;

и

-

k

если k = D₂ n ² j ², то

W j ( t ) = Y exp( - D 2 П ² j ² 1 ) +

u ₂ B ² _j

D ₂ n ² j ²

+

при

в =

-

+ ( k

u ₁ B ¹ _j

D 1 n ² j j

-

и ₂ B j ) t exp( - kt ) +

+ в exp( - ( k + D 1 n ² j ²) t )

ku ₁ B ¹ _j

-

u ₂ B ² _j

D 1 n ² j ² ( D 2

D ₂ n ² j ²

-

в •

-

D 1 ) n ² j j

-

k

и

Y =

Средний момент второго порядка для продукта реакции выражается громоздкой формулой:

< и 2 >= 2 u ₂ B 02

, r 2 1 2 . r i 1 - (1 + kt )exP( — kt ). ^u i B о ^{- u} 2 B 02 L 1 — ^ex P( — kt ) )

U₇B_nU i B n11 t

• ^{2    0} 2     ^{1 0} k ²                    k ( k J

1 - exp( - kt )    A ²                          2 - (2 + 2 kt + k ² t ²)exp( - kt )

+ 2D2t - 2D2-----p---+ — (1 - exp(-kt)) + (u 1B0)2--- k 3                                       k2

+ 2 D ₁

1 - (1 + kt ) exp( - kt )    u 2 у ⁽ B °^{) 2} 1 - (1 + kt )exp( - kt )

k            D1 у n2 j2          k ku2 у (B])2 1 -exp(-kt) 1 -exp(-(k + D1n2j2)t) ~d[ ^ п4 j4 [ k            k + D1n2 j2

+Уи 2 B j

u ₂ B ² _j

D п ² j ²

t + _y 1 ^- exp( ^- D 2 ^{n 2} j ² t ) + ^ 1 - exp( - kt ) + _в 1 ^- exp( ^- ( k + D n ² j ²) t ) D ₂ n ² j ²                k                k + D₁ n ² j ²

.

В случае совпадения конвективных профилей и коэффициентов диффузии продукта и реагента, дисперсии их пиков будут совпадать. Этот вывод также совпадает с выводом работы [17]. При этом управляющими параметрами являются как абсолютные значения, так и отношения одноименных величин: конвективных скоростей ( u 1 / u 2 ); параметров клиновидности ( m ₁/ m ₂); коэффициентов диффузии продукта и реагента ( D 2 / D 1 ); а также константа скорости реакции k , длина (объем) пробки A и время анализа t .

Управление состоянием поверхности микроканала

Обоснование данного способа управления иллюстрируется следующей логической цепочкой:

• 2 . Малая концентрация водоподобного буфера С 0 (10^–6–10^–4 М). Как следствие — относительная диэлектрическая проницаемость Е =80 (воде соответствует значение 81).

• 3 . Величина дзета-потенциала ^₀ лежит в пределах 10–100 мВ. В этой ситуации коэффициент в = ( F ^ 0 )/(RT ) <  1 и возможна линеаризация sh( в^ ) = в^ ( F и R обозначают соответственно постоянную Фарадея и универсальную газовую постоянную).

Тогда уравнение для скоростного профиля из системы Пуассона—Больцмана примет вид:

U(z) = 2£6,ЕЕ„садГ]- CW ^ п ( ch(2) J где в явном виде X = Fh^C0 /(ее0RT), Е — напряженность продольного управляющего электрического поля, п — динамический коэффициент вязкости, Е0 — электрическая постоянная ( е0 =

10 7            __-12

=---- = 8.842 • 10 ¹ ф/м ). Решение уравнений

4 п с ²

и обоснование соответствующих граничных условий также приведены в [6].

Аппроксимация (5) степенным профилем U(z) = Umax(1 - zm) проводится в соответствии с несколькими возможными критериями оптимизации, связанными с близостью двух профилей скорости. Предложенные критерии, позволяющие связать параметр X, определяющий толщину двойного электрического слоя, и параметр клиновид- ности конвективного профиля m обсуждены в работе [13].

Важнейшей особенностью аппроксимации (5) является то, что показатель клиновидности профиля m не зависит от величины дзета-потенциала, коэффициента динамической вязкости и от напряженности электрического поля. От этих параметров зависит абсолютная величина скорости, а не ее распределение по сечению канала. Однако при неприменимости линейной аппроксимации гиперболического синуса, то есть когда β ≥ 1, что осуществляется при превышении дзета-потенциалом некоторого порога, не только средняя скорость, но и параметр клиновидности m будут зависеть и от величины дзета-потенциала, и от коэффициента динамической вязкости, и от напряженности электрического поля.

Создание управляемого температурного поля

Концепция данного нового способа управления заявлена в работе [13]. Ее обоснование также связано с уравнениями Пуассона—Больцмана, поскольку даже в линейную аппроксимацию (5) входит в явном виде температура. Эта концепция управления может быть реализована, исходя из трех алгоритмов различного уровня сложности и требующих различного ПМО. Во всех случаях основным критерием оптимального выбора управляющего температурного поля является наилучшее разрешение аналитических пиков компонент.

Были предложены и охарактеризованы следующие три основных алгоритма [13].

Алгоритм 1. Варьирование постоянной во всем канале температуры Т или применение микрогаба-ритных нагревателей для формирования продольных градиентов теплового поля.

Алгоритм 2. Задание начальной температуры и граничных условий на стенках канала с изменением Т естественным путем (действие управляющего электрического поля).

Алгоритм 3. Задание продольного градиента температуры для оптимального управления процессом разделения компонент с перспективой внедрения следящей системы управления температурой, "отслеживающей" прохождение быстрых компонент с более узкими пиками и меняющей температуру (скоростной профиль, коэффициент диффузии и, следовательно, закон формирования пика более медленных компонент) с целью сужения пика последних и достижения лучшего разрешения.

ОБРАБОТКА ИНФОРМАТИВНЫХ СИГНАЛОВ

Поскольку решение задачи поиска эффективного алгоритма обработки информативных сигналов влияет на качество анализа, то опосредовано ре- зультаты данного направления работ представлены в [1–5, 7, 9, 10]. Однако подход к поиску алгоритма обработки информативных сигналов и его применение более детально описаны в работах [8, 11, 14].

Основания для применения специальных дополнительных алгоритмов обработки аналитических сигналов (пиков) в приборах электрофореза на микрочипах следующие: 1) переход к пиколитровым диапазонам анализируемых объемов (т.е. уменьшение анализируемых объемов на 3–5 порядков по сравнению с классическим капиллярным электрофорезом) приводит к уменьшению амплитуды информативного сигнала (уменьшению отношения сигнал/шум); 2) сокращение времени анализа (от 3 до 10 раз) приводит к сужению пиков. Таким образом, традиционная модель аналитического пика — кривая Гаусса оказывается неадекватна. Также следует заметить, что именно на модель гауссианы ориентированы традиционные критерии разрешения пиков.

Очевидно, что изменение отношения сиг-нал/шум существенно осложнит на практике алгоритм разрешения альтернативы "пик/шум": огрубление алгоритма (увеличение пикового порога) приведет к возрастанию ошибок первого рода — пропуск истинных пиков компонент, неизменность традиционных порогов приведет к резкому возрастанию ошибок второго рода — принятию шумов в качестве пиков (ложных). Кроме того, большие шумы существенно осложнят задачи выделения базовой линии, определение границ и центра тяжести пика. Сокращение времени анализа приведет к необходимости замены адекватных моделей пика на треугольную (кусочно-линейную) и параболическую [14]. Также заметим, что для узких островершинных (треугольных) пиков

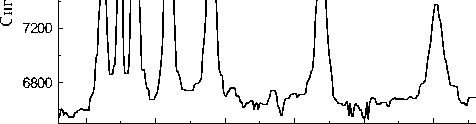
1000     1050     1100     1150     1200     1250

Такт

Фрагмент электрофореграммы разделения смеси олигонуклеотидов Аmix (10, 20, 30, 40, 50, 75 и 100 оснований). Один такт составляет 0.2 с серьезной проблемой будет расчет площади пика.

Типичный фрагмент электрофореграммы на микрочипе представлен на рисунке. Очевидно наличие на рисунке нескольких ложных пиков (в области 1130 и 1200 тактов). Также следует отметить, что гауссова модель может быть применена лишь к последнему (правому пику). Пики 2–4 (отсчет слева), наверное, следует аппроксимировать треугольником, остальные — параболой.

Предложенный в работе [14] и подтвержденный результатами [8, 11] подход к обработке аналитических сигналов базировался на использовании цифрового фильтра (тангенсный фильтр Баттерворта второго порядка). Алгоритм включал две стадии: а) префильтрация цифровым фильтром нижних частот (ФНЧ) с частотами среза 0.03–0.12 от частоты дискретизации (съема данных); б) обратный пересчет амплитуды пика, ширины, площади отфильтрованных сигналов к исходным по соответствующим таблицам.

ЗАКЛЮЧЕНИЕ

Благодаря использованию метода математического моделирования были получены следующие основные результаты.

• 1.    Анализ, по крайней мере на уровне концепций, всех пяти предложенных способов управления процессом анализа смесей на микрочипе показал их обоснованность и эффективность.

• 2.    Предложенная базовая модель плоской щели позволяет использовать метод моментов для оценки параметров аналитических пиков компонент и тем самым выбрать управление анализом, варьируя ширину микроканала, объем пробы и точку детектирования (или время анализа). В свою очередь, модификация модели на трехмерный случай позволит решать аналогичную задачу применительно к каналам прямоугольного и трапеции-дального сечения. В последних в качестве дополнительных управляющих параметров могут выступать глубина канала и угол наклона стенок.

• 3.    На основе метода моментов в рамках базовой модели плоской щели получено явное выражение (3) для центра тяжести и средней дисперсии пиков продукта и реагента. Эти выражения содержат в качестве управляющих параметров нормированные значения максимальных конвективных скоростей, коэффициентов диффузии и константу скорости химической реакции первого порядка k . Выражение для дисперсии продукта имеет весьма громоздкий вид (4). В случае равенства скоростных профилей и коэффициентов диффузии продукта и реагента характеристики их аналитических пиков будут одинаковыми.

• 4.    Модификация поверхности микроканала (величина дзета-потенциала) также позволяет управ-

• лять анализом. Однако методика управления характеризуется следующими особенностями. Если величина дзета-потенциала не достигла некоторого минимального порога (порога применимости линейных аппроксимаций уравнений системы Пуассона—Больцмана), то: а) ее изменение не влияет на степень клиновидности профиля m, однако б) это изменение влияет на масштаб конвективной скорости, который прямо пропорционален величине дзета-потенциала (5).

• 5.    Применимость температурных полей для управления анализом на микрочипе исследовалась ранее в работе [13]. В указанной работе оценивалось влияние вариации температуры только на толщину двойного электрического слоя (параметр λ ) или на параметр клиновидности скоростного профиля. Выявлена низкая чувствительность m = m ( T ). Однако способ управления может учитывать действие других тепловых эффектов — изменение динамической вязкости, коэффициента диффузии и т.д.

• 6.    Фильтрация информативного сигнала, представленного на рисунке, показала наибольшую эффективность применения ФНЧ с относительными частотами среза 0.06–0.09: выбор большей частоты среза фильтра ухудшает качество подавления шумов, использование меньших частот приводит к очень сильным деформациям формы пиков — резкому уменьшению амплитуд для треугольных пиков и существенному расширению и асиммет-ризации параболических пиков.