Моделирование процессов теплообмена, протекающих в пластинчатых теплообменных аппаратах

В настоящее время в России теплоснабжение зданий осуществляется от центральных тепловых пунктов по внутриквартальной системе трубопроводов. Теплоноситель поступает в системы отопления через элеваторные узлы, установленные в каждой секции здания. Данные узлы обладают следующими основными недостатками:

• 1.    Температуру теплоносителя, подаваемого в систему отопления, невозможно изменить при изменении режимов эксплуатации здания (например, температуры наружного воздуха).

• 2.    Центральный тепловой пункт (ЦТП) используется для обслуживания группы зданий, в связи с чем не удается учесть индивидуальные особенности каждого из них.

• 3.    Элеватор не обеспечивает надежную циркуляцию теплоносителя в системе отопления в условиях нестабильности давления в поквартальной сети.

• 4.    Обязательными условиями перехода на расчеты с владельцами жилья по фактическим затратам тепла на отопление являются наличие термостатов на каждом отопительном приборе, автоматическое поддержание в зданиях температурного графика в системе отопления, а также стабилизация параметров горячей воды. Эти мероприятия невозможно осуществить при наличии элеваторного узла в здании.

Для решения задач оптимизации систем отопления зданий определены основные положения концепции внедрения современных энергосберегающих технологий:

• –    индивидуальное автоматическое регулирование теплоотдачи отопительных приборов посредством установки на них термостатических вентилей;

• –    автоматическое регулирование температуры теплоносителя на вводе в каждое здание в зависимости от температуры наружного воздуха и обеспечение насосной циркуляции теплоносителя в системе отопления; учет расхода тепловой энергии;

• –    автоматическое регулирование температуры теплоносителя и стабилизация параметров воды контуров горячего водоснабжения.

2.    Постановка задачи 3.    Математическая модель пластинчатого теплообменного аппарата

Использование индивидуальных тепловых пунктов (ИТП) на вводах в здания, реализованных на базе водо-водяных пластинчатых теплообменных аппаратов (ПТА), позволяет создавать домовые автоматизированные узлы управления потреблением тепловой энергии и ее учета ( Зингер и др ., 1995).

Внедрение современных средств автоматизации способствует оптимизации затрат на потребляемую тепловую энергию, а также расходов на эксплуатацию систем отопления и их профилактику, что в итоге позволяет экономить на содержании здания. Отпуск тепла и его потребление – это емкие и информативные параметры, лежащие в основе теплотехнических и экономических расчетов. Исследование эффективности методов управления потреблением тепловой энергии возможно только при наличии математических моделей объектов управления. Для пластинчатых теплообменников, которые в настоящее время широко используются в системах теплоснабжения, применима модель "вытеснение – вытеснение" (Жукаускас, 1982).

Математические модели позволяют исследовать возможности применения регуляторов, обеспечивающих автоматическое управление температурой теплоносителя на вводе в каждое здание в соответствии с заданным для этого здания температурным графиком.

В настоящей работе представлена математическая модель теплообменного аппарата, которая учитывает передачу энергии от греющего контура нагреваемому контуру (в отличие от существующих моделей теплообменных аппаратов, учитывающих передачу энергии через стенку аппарата воде). Полученная модель позволяет опр еделить возможности реализации алгоритмов эффективного управления потреблением тепловой энергии. Результаты исследований свидетельствуют о том, что процессы, протекающие в модели ПТА, носят распределенный характер, а реализованное сосредоточенное нечеткое управление способствует решению задач оптимизации работы системы управления ( Прохоренков , 2000).

Рассмотрим тепловые процессы, протекающие в водо-водяном противоточном пластинчатом теплообменном аппарате, упрощенная схема которого представлена на рис. 1.

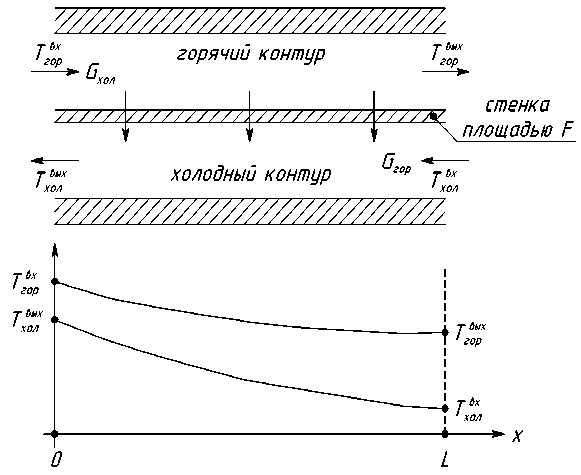
Рис. 1. Схема противоточного водо-водяного ПТА

Вода горячего контура проходит между пластинами аппарата, условно показанными в виде стенки, разделяющей два водяных контура, охлаждается, отдавая тепло пластинам, а через них – воде холодного контура, нагревая в нем воду ( Уонг , 1979). Движение теплоносителей противоточное.

Исходя из уравнений закона сохранения энергии, динамика водо-водяного теплообменного аппарата описывается системой одномерных линейных дифференциальных уравнений в частных производных:

^{d T ( x}, t ) ₊ V¹

d t

^d T '^{( x} , t ) = Л ( T cm ( x , t ) - T ' ( x , t )). d x      T

<

"т. ( x, t ) = C 1 ( T ' ( x, t ) - T m ( x , t ) ) - C 2 ( T , ( x, t ) - T " ( x , t ) ) , dt

^d T I ^{( x}, t ) ₊ V I d t

d T"(x, t) = 4 Tm (x, t)-T" (x, t ))• T dx

В данных уравнениях приняты следующие обозначения: T ^I( x , t ) – температура движущейся в первичном контур е греющей воды в сечении аппарата x в момент времени t ; T ^II( x , t ) – температура движущейся во вторичном контуре нагреваемой воды в сечении аппарата x в момент времени t ; T _ст ( x , t ) – температура стенки поверхности, через которую осуществляется теплообмен между водой первичного и вторичного контур ов, в сечении аппарата x в момент времени t .

Коэффициенты V ^I, V ^II, м/с, линейных скоростей греющей в первичном контур е и нагреваемой во вторичном контуре воды определяются по формулам:

V ' = —G ---’ V

^S сеч ^P в

II

GII

,

S^U /7

° сеч ^p в

где G ^I, G ^II – массовый расход греющей в первичном контуре и нагреваемой во вторичном контуре воды, кг/с; p в – плотность воды, кг/м³; S ^I сеч , S ^II сеч – площадь поперечного сечения одного хода теплообменника со стороны I и II контуров, м².

Коэффициенты τI, τII, с, рассчитываются по следующим формулам:

I _ ^S сеч ^Lp B c p в    _ц    Sce^4^L P scp в

T — I —    , T —------7,------ , a f      ат где αI – коэффициент теплоотдачи от греющей воды первичного контура к стенке поверхности теплообмена, Вт/(м2∙°С); αII – коэффициент теплоотдачи от стенки поверхности теплообмена к нагреваемой воде вторичного контура, Вт/(м2∙°С); F – площадь поверхности теплообмена, м2; L – длина поверхности теплообмена (точнее, длина проекции поверхности теплообмена), м; cрв – теплоемкость воды, Дж/(кг∙°С).

Коэффициенты C 1 и C 2 , c^–1, определяются по формулам:

C — ^a S сеч , C — ^a S сеч ,

С cm m ст           С cm m ст где Cст – удельная теплоемкость металла стенки между греющей и нагреваемой водой теплообменника, Дж/(кг∙°С); mст – масса стенки теплообменника между греющей и нагреваемой водой, кг.

Разобьем пространственную координату x на N равных дискретных участков длиной ∆x . Тогда можно записать

∆x = L / N .                                            (2)

С учетом формулы (2) принимаем конечно-разностную аппроксимацию частных производных по координате x в виде

d T ' ( x , t ) _ d x	T ^^ ^- T -1( ) , —- 1, K , ( N — 1 X 2 Д x Tl^l-lAM , , — N , Д x
d T n ( x , t )	[ T i +-( t )- T i П1( 1 ) , i — 1, K , ( N - 1 ) , 2 Д x

= <

d x	T” ( t ) - T i "( t ) , i — N . Д x

На основании данных приближенных выражений преобразуем исходную систему уравнений (1)

У                 [ T ' ( t ) — T' T ХЛt ) + T ' ( 0 ) + J ( AT' ( t ) + B I T ст ( t    ,

' T ст ( t ) — T ст ( 0 ) + J ( c 1 T ' ( t ) + C 2 ( R' T " ( t ) ) - ( C 1 + C 2 ) T ст ( t ) ) dt , T '' ( t ) — T 'T“ ( t ) + T '' ( 0 ) + J ( A '' T '' ( t ) + B '' ( R ' T _ст ( t ))Vt .

В ней матрицы распределения температур греющей, нагреваемой воды и стенки по длине теплообменника обозначены T I( t ), T II( t ), T ст ( t ) соответственно. Элементы этих матриц могут быть
представлены следующим образом:
	f T 0 '' = T “ ( t ) ^		f T 0 ' - T вх ( t ) "	( T     (f ) T ст 0 ( t )
	T , '' ( t )		T , ' ( t )	T ст 1 ( t )
	T 2 '' ( t )		T 2 ' ( t )	T ст 2 ( t )
T "  ( t ) —	M	, T - ( t ) —	M	, T „. ( t ) —             M	.
	T N' - 2 ( t )		T N - 2 ( t )	T ст N - 2 ( t )
	T N' - , ( t )		T N - 1 ( t )	T ст N - 1 ( t )
	I T N' = T вЫх ( t )v		I T N - T вЫх ( t ) ,	l T ст N ( t ) ;

Начальные условия, заданные в виде матриц и характеризующие распределения температур греющей воды T ^I(0), нагреваемой воды T ^II(0) и стенки T ст (0) по длине теплообменника в начальный момент времени t = 0, а также граничные условия, характеризующие изменение во времени температур воды на входе в теплообменник как со стороны первичного T ^I вх ( t ), так и со стороны вторичного контуров T ^II вх ( t ), представим в виде

	0		r 0           1		Г T ст 0 ( 0 ) "		r 1 1
	T 1 ( 0 )		T” ( 0 )		T ст 1 ( 0 )		0
	T 2 1 ( 0 )		T 2 1 ( 0 )		T ст 2 ( 0 )		0
T1 ( 0 ) =	M T NI - 2 ( 0 )	, T1 40 ) =	M T N - 2 ( 0 )	, T ст ( 0 ) =	M T ст N - 2 ( 0 )	, T '-	M 0
	t N - 1 ( 0 )		T N - 1 ( 0 )		T„ N - 1 ( 0 )		0
	I t N ( 0 ) = t Выа ( 0 ) J		I T N ( 0 ) = T ы ( 0 ) j		, T„ , ( 0 ) J		к 0 J

Матрицы A ^I и A ^II, связывающие соседние участки ∆x теплообменника, зависят от линейных скоростей (значит, и от расхода) воды в соответствующем контуре и рассчитываются так:

			A	1 = V1 2 A x	A ' +	1 T A	A11 =	V 2 A x	A ' +	— A "  , T
	Г 0	0	0	0	0	0 1		Г 0	0	0	0	0	0 1
где	1	0	-1      •	0	0	0		0	- 1	0 L	0	0	0
	0	1	0	0	0	0		0	0	- 1	0	0	0
A =	0	0	0	0	- 1	0	, A -=	0	0	0	- 1	0	0
	0	0	0	1	0	- 1		0	0	0 L	0	- 1	0
	I 0	0	0	0	2	- 2 j		1 0	0	0	0	0	- 1 J

Матрицы B ^I и B ^II, характеризующие влияние температуры стенки на первичный и вторичный контуры соответственно, вычисляются следующим образом:

B¹ = -1- B' , B ¹ = -1 B' , t         T ¹

где r 0 ^

B ' = M .

к 1 J

Матрица, служащая для согласования матриц распределения температур греющей и нагреваемой воды при противотоке в теплообменнике, имеет вид

Г 0	0	0	0	0	1 1
0	0	0 L	0	1	0
0	0	0	1	0	0
0	0	1	0	0	0
0	1	0 L	0	0	0
1 1	0	0	0	0	0 J

На рис. 2 представлена укрупненная структурная схема модели теплообменника, составленная на основании данной системы уравнений. Блоки, обозначенные цифрами на рисунке, описываются соответствующими уравнениями системы (1).

Детализованная структурная схема представлена на рис. 3.

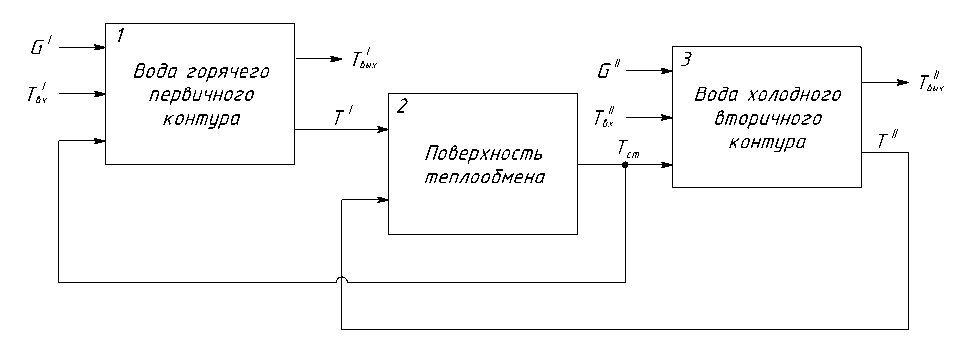
Рис. 2. Структурная схема модели теплообменника

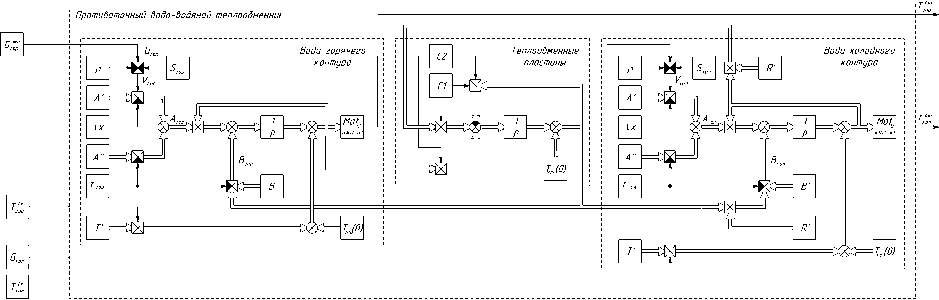
Рис. 3. Структурная схема модели пластинчатого теплообменного аппарата

4.    Разработка регулятора температуры горячей воды

В процессе анализа принципов построения адаптивных систем автоматического управления (САУ) выявлен ряд трудностей, возникающих при решении задач синтеза таких систем ( Коломойцева , Хо , 2002). Одной из них является выбор метода настр ойки параметров управляющих устр ойств, которая может быть осуществлена с помощью существующих методов только в частных случаях. Наличие блока идентификации динамики объекта управления и оценка переменных состояния усложняют структуру САУ. Кроме того, погрешность идентификации ухудшает качество управления, а в некоторых случаях приводит к неустойчивому режиму работы САУ. Применение аппарата нечеткой логики для построения адаптивных систем связано с формализацией неточных, размытых в смысловом отношении суждений и обобщенных категорий, задающих классификацию исходных понятий на уровне нечетких множеств, что весьма важно при управлении объектами, описание которых известно неточно. Это дает возможность создавать адаптивные системы с оптимальным управлением, которое может быть аппроксимировано выходной переменной нечеткого регулятора ( Мирошник и др. , 2000). Синтез адаптивных нечетких регуляторов св одится к решению некоторого конечного множества оптимизационных задач, при этом вид оптимизационной функции зависит от данных обучающей выборки. Нахождение глобального экстремума такой функции традиционными методами оптимизации является сложной, а часто нерешаемой задачей.

Основной задачей, решаемой средствами автоматизации подсистемы горячего водоснабжения (ГВС), является поддержание температуры горячей воды в заданном диапазоне. Регулирование температуры горячей воды Т г во вторичном контуре теплообменных аппаратов осуществляется посредством изменения подачи теплоносителя в первичный контур. Функциональная схема автоматизации процесса регулирования температуры воды в подсистеме ГВС представлена на рис. 4.

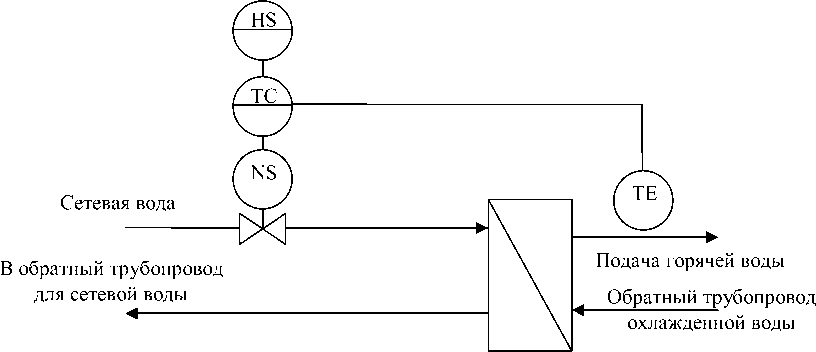
Рис. 4. Функциональная схема автоматизации процесса регулирования температуры горячей воды в подсистеме ГВС: HS – задатчик температуры; TE – датчик температуры; TC – регулятор температуры; NS – пусковая аппаратура регулирующей заслонки

Наиболее характерными возмущениями для вторичного контура подсистемы ГВС являются изменения:

• -    расхода жидкости во вторичном (холодном) контуре;

• -    температуры воды, подаваемой в первичный (горячий) контур теплообменника.

Методика синтеза регулятора температуры для реализации алгоритма функционирования контура ГВС включает разработку модели управления объектом и структуры регулятора для данного объекта, а также настройку параметров регулятора.

Имитационная модель управления объектом, формализованная в виде правил, имеет следующий вид:

• -    если уменьшить подачу теплоносителя в теплообменник, то Т _г будет убывать;

• -    увеличить подачу теплоносителя в теплообменник, то Т _г будет возрастать.

Регулирование Т _г будем осуществлять с помощью контроллера, реализующего алгоритм нечеткого управления Мамдани.

На основании экспериментальных данных и экспертных оценок получим следующие лингвистические переменные (параметры) объекта управления:

• 1.    Абсолютное значение температуры Т _г ( t ) в момент времени t характеризуется набором лингвистических переменных: "высокая", "нормальная", "низкая"; функции принадлежности р( Т _г) нечетким множествам "высокая", "нормальная", "низкая" - линейными уравнениями вида у = kx + b .

• 2.    Относительное изменение температуры А Т _г за время t ₀ (такт алгоритма расчета) определяется набором лингвистических переменных: "увеличивается", "уменьшается".

Процесс фазификации состоит в установлении соответствия между измеренными значениями Т _г( t ), А Т _г( t ) и нечеткими множествами р( Т _г), р(А Т _г), т.е. в вычислении соответствующих коэффициентов функции принадлежности.

Для управления U ( t ) в момент времени t вычисляются лингвистические переменные "открыть", "закрыть" .

Процесс нечеткого ввода заключается в установлении соответствующих нечетких множеств для управления U ( t ) (коэффициентов принадлежности) при известных значениях функции принадлежности р( Т _г) и р(А Т _г). Алгоритм управления формализуется в виде следующего набора правил:

• -    если Т_г - "низкая", то U1 - "открыть";

• -    Т_г - "высокая", то U1 - "закрыть";

• -    АТ_г - "увеличивается", то U₂ - "закрыть";

• -    АТ_г - "уменьшается", то U₂ - "открыть".

5.    Исследование модели теплообменного аппарата

Набор основных правил работы нечеткого регулятора представлен на рис. 5.

Задающим параметром регулирования является температура подаваемой потребителю горячей воды Т ⁰_г = 55 °С. Допустимый диапазон изменения температуры Т г составляет от 50 до 60 °С.

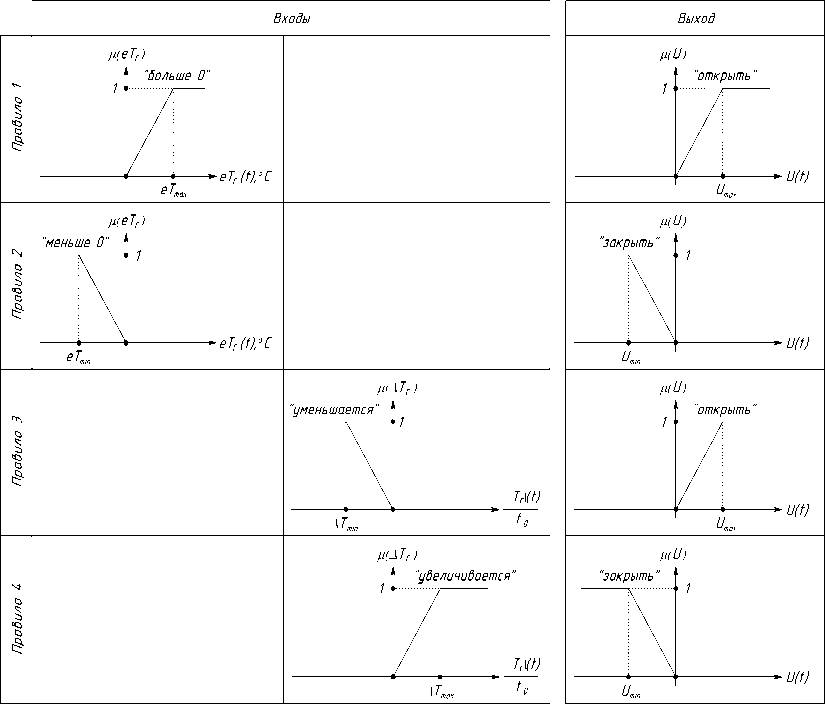
Рис. 5. Набор правил работы нечеткого регулятора

Необходимо отметить, что процессы, протекающие в математической модели пластинчатого теплообменного аппарата, носят распределенный характер, а реализованное сосредоточенное нечеткое управление дает возможность оптимизировать работу системы управления.

На основании структурной схемы (рис. 3) в пакете Simulink программы MatLAB был разработан блок, реализующий полученную модель теплообменного аппарата (рис. 6).

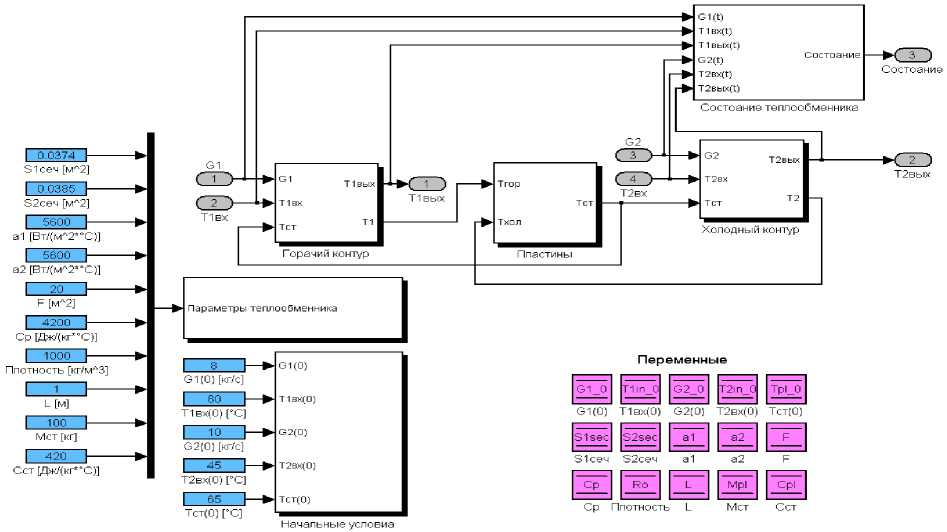
Рис. 6. Модель ПТА, реализованная в пакете Simulink программы MatLAB

Значения используемых при моделировании параметров исследуемого пластинчатого теплообменного аппарата ( Коломойцева, Хо , 2002) представлены в таблице.

Таблица. Значения параметров моделируемого теплообменника

Обозначение	Значение	Единица измерения
S 1сеч	0,0385	м2
S 2сеч	0,0385	м2
α 1	5600	Вт/(м2∙°С)
α 2	5600	Вт/(м2∙°С)
F	20	м 2
С p	4200	Дж/(кг∙°С)
ρ	1000	кг/м3
L	1,12	м
М ст	100	кг
с, ст	420	Дж/(кг∙°С)

Результаты моделирования процессов теплообмена, протекающих в пластинчатых теплообменных аппаратах, при различном числе N дискретных участков разбиения представлены на рис. 7-9.

Анализ полученных результатов моделирования показал, что при разбиении пространственной координаты x длины проекции поверхности теплообмена L на большее число дискретных участков происходит изменение ∆x , приводящее к уточнению модели. Из графиков переходных процессов (рис. 8 и 9) видно, что снижение расхода воды в нагреваемом контуре не приводит к изменению температуры греющей воды на выходе из теплообменника.

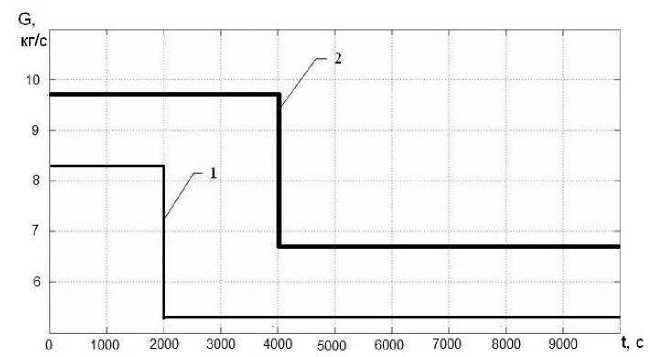
Рис. 7. Графики изменения расхода воды в греющем (1) и нагреваемом (2) контурах теплообменника

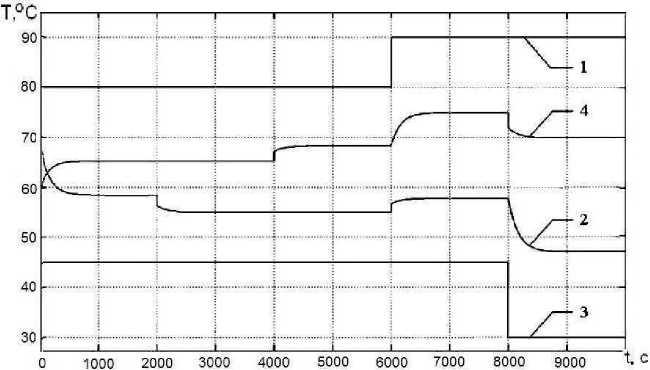
Рис. 8. Переходные процессы, происходящие при изменении температур греющей (1, 2) и нагреваемой (3, 4) воды на входе (выходе) теплообменника (при N = 1)

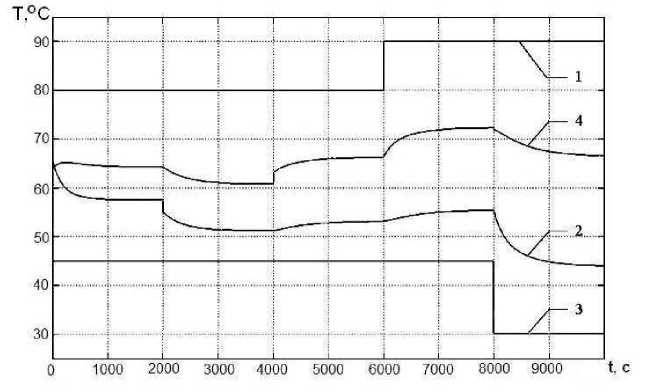
Рис. 9. Переходные процессы, протекающие при изменении температур греющей (1, 2) и нагреваемой (3, 4) воды на входе (выходе) теплообменника (при N = 20)

6.    Исследование работы контура стабилизации температуры горячей воды

Модель пластинчатого теплообменного аппарата, реализованная в программе MatLAB, была использована в процессе моделирования контуров стабилизации температуры горячей воды с учетом параллельно работающих теплообменника отопления и теплообменника I ступени подогрева горячей воды. Модель контура стабилизации (рис. 10) была построена таким образом, чтобы обеспечить подачу горячей воды без потерь, а при отсутствии отбора воды потребителями предусмотрена циркуляция нагретой воды в сети ГВС. Управление температурой горячей воды в контуре ГВС осуществляется с помощью нечеткого регулятора, результаты работы которого представлены на рис. 11.

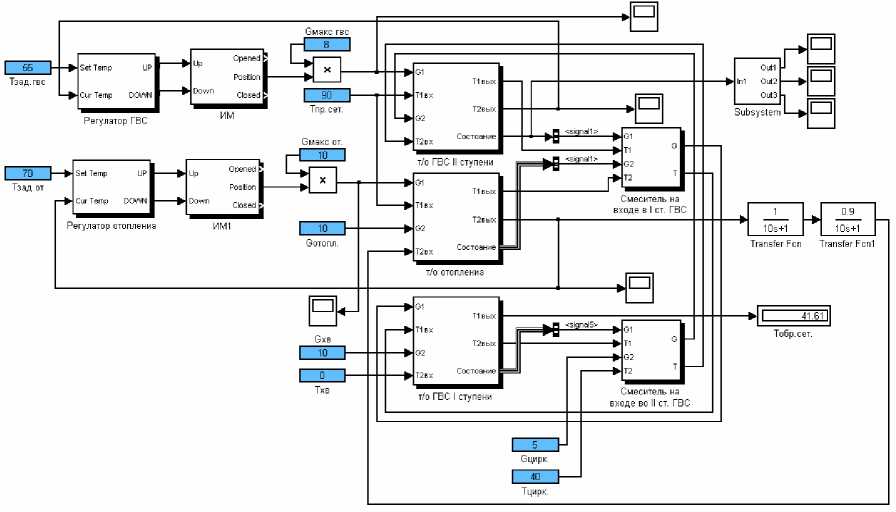
Рис. 10. Модель контура управления ГВС

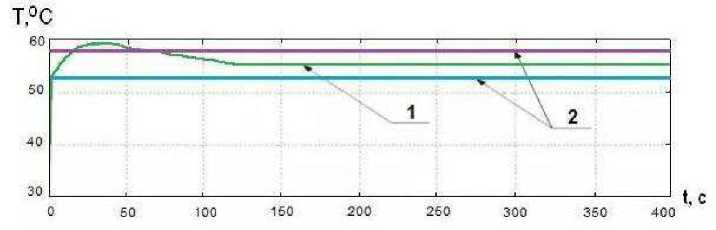
Рис. 11. График изменения температуры в контуре ГВС при работе нечеткого регулятора:

1 – график изменения температуры ГВС; 2 – диапазон допустимых значений изменения температуры ГВС

7.    Заключение

Анализ полученных результатов исследования показал, что разработанная модель ПТА может применяться в контурах регулирования температуры систем отопления и горячего водоснабжения, а также при выполнении исследовательских и проектных работ по реконструкции систем теплоснабжения.