Моделирование процессов в топливной системе ракет-носителей при наличии демпфера продольных колебаний

В данной работе предложена математическая модель для проведения предварительных инженерных оценок параметров топливной системы ступени ракеты-носителя (РН) при наличии демпфера продольных колебаний. Демпфер устанавливается на расходной магистрали РН с целью недопущения колебаний топлива, которые в конечном итоге могут вызвать рост давления в расходной магистрали, превысить давление опрессовки и, в результате, привести к разрушению расходной магистрали.

Актуальность работы состоит в необходимости проведения предварительных инженерных оценок ряда параметров топливной системы на ранних стадиях проектирования перспективных РН. К числу таких параметров относятся как параметры самого демпфера, так и параметры всей пневмогидравлической системы подачи при наличии системы демпфирования, а именно: диапазон давлений на входе в двигатель, уровень компонента топлива (КТ) в демпфере (с целью оценки риска прорыва пузыря в расходную магистраль КТ), допустимые диапазоны объёмной жёсткости демпфера продольных колебаний. Объёмная жёсткость определяет возможности демпфера в части выполнения своей основной функции — гашении продольных колебаний столба жидкости [1–4].

Практическая значимость работы состоит в том, что рассматривается конструкция демпфера, в котором в течение всей циклограммы полёта РН осуществляется наддув газовой полости демпфера и дренаж из его полости в атмосферу [3, 4]. Ранее использовался тип демпфера со свободной газовой полостью — выносная ёмкость, частично заполненная жидкостью (КТ), частично — газом. Либо же использовался тип демпфера с наддувом и дренажем, но без свободной поверхности. Жидкость и газ в демпфере были разделены сильфоном.

Кроме того, в работе рассматриваются методы оценки расходов газожидкостной смеси через дренажную магистраль демпфера, оценка критической высоты КТ над уровнем среза дренажа, на котором начинаются воронкобра-зование и прорыв газожидкостной смеси (ГЖС) в дренажную магистраль.

На основании представленной в работе математической модели выполнены оценки ряда параметров пневмогидравлической системы при наличии демпфера продольных колебаний. Их результаты были сопоставлены с результатами эксперимента.

1. Постановка задачи

В данной статье рассматривается задача по моделированию процессов в топливной системе ступени ракеты-носителя при наличии демпфера продольных колебаний, устанавливаемого на расходной магистрали (РМ), по которой топливо подаётся из топливного бака в маршевый двигатель (МД) РН (рис.1, 2).

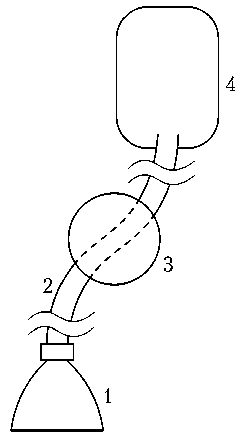
Рис. 1. Общая схема расположения демпфера продольных колебаний на расходной магистрали: 1 — маршевый двигатель; 2 — расходная магистраль компонента топлива; 3 — демпфер продольных колебаний; 4 — топливный бак (рисунок создан автором)

В рамках данной схемы рассматривается задача, в которой требуется оценить:

• •    диапазон изменения давления на входе в МД ступени РН;

• •    возможность удержания уровня КТ в демпфере не ниже заданного в течение работы МД. Данное требование обусловлено необходимостью недопущения прорыва газа и подушки в расходную магистраль КТ и резкого увеличения газосодержания на входе в МД;

• •    нахождение значений объёмной жёсткости демпфера в установленных на режиме работы МД границах, определяющих отсутствие колебаний в топливной системе РН.

Для решения данной задачи в работе рассматривается математическая модель, которая будет подробно описана ниже.

Допущения в модели:

• •    не учитывается возможное влияние «запирания» при течении ГЖС (т. е. отсутствует учёт скорости звука в ГЖС в магистрали дренажа демпфера);

• •    в целях упрощения расчёта процессов в демпфере термодинамический процесс предполагается близким к изотермическому.

• 2. Математическая модель

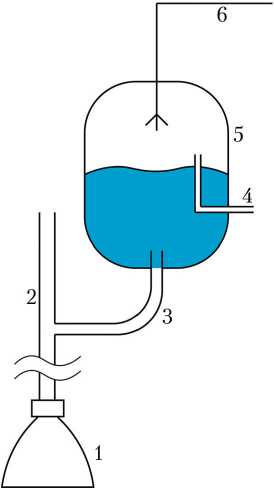
Рис. 2. Концептуальная схема рассматриваемой задачи: 1 — маршевый двигатель; 2 — расходная магистраль компонента топлива; 3 — соединительная магистраль между демпфером продольных колебаний и расходной магистралью; 4 — дренажная магистраль демпфера; 5 — каркас демпфера; 6 — газовод наддува демпфера (рисунок создан автором)

В рамках рассматриваемой математической модели увязываются в единую систему уравнений процессы в газовой и жидкостной полости демпфера, в газовой полости топливного бака РН, процессы в расходной магистрали РН и процессы в магистрали, соединяющей полость демпфера и расходную магистраль РН. К числу особенностей рассматриваемой в работе математической модели можно отнести то, что она позволяет учесть воронкообразование над срезом дренажной магистрали демпфера

и, соответственно, рассчитать течение ГЖС через дренажную магистраль.

На основании закона сохранения

массы, уравнения состояния газа и вто-

рого закона Ньютона выведем систему уравнений для рассматриваемой задачи.

На основании второго закона Ньютона запишем уравнение для

компонента топлива в расходной

магистрали (РМ) [5, 6]

бак вх.дв

– P сопр

+ ρ _КТ n_x gH _РМ ) S _РМ

= m

dU _РМ ст _dt ^;

m ст ⁼ ρ КТ ^S РМ ^H РМ^;

сопр ^ζ местн    ^ζ трен

РМ

^{2 ρ} КТ ^S Р ² М

^G РМ

^ρ КТ ^S РМ ^U РМ^,

где P _бак — давление в топливном баке; P _вх.дв — давление на входе в двигатель; P _сопр — падение давления в РМ; ρ _КТ — плотность КТ; n_x — перегрузка; g — ускорение свободного падения; H _РМ — высота столба КТ в РМ; S _РМ — площадь сечения РМ; m _ст — масса столба КТ в РМ; U _РМ — скорость КТ в РМ; ζ _трен , ζ _местн — коэффициенты гидравлических сопротивлений трения и местных сопротивлений в РМ; G _РМ — массовый расход КТ в РМ.

На основании закона сохранения массы запишем уравнение для расходов через топливную систему:

сопротивления и площадь поперечного сечения переливной магистрали, соединяющей демпфер и РМ, соответственно.

При этом G _демпф > 0, если КТ заходит в демпфер; G _демпф < 0, если КТ выходит из демпфера.

На основании уравнения состояния газа в газовой полости демпфера получаем следующее выражение:

d dt

демпф под

RT

= G

надд

G , др

G РМ

G двиг

+ G

демпф,

где G _двиг — расход КТ, идущий в двигатель; G _демпф — расход КТ, идущий в демпфер.

Продифференцируем уравнение (5). Принимая во внимание, что расход, идущий на двигатель, постоянный, получим

^dG РМ ₌ демпф dt dt

На основании закона сохранения массы запишем уравнение для расхода КТ в демпфере:

dG        dV демпф               под dt = –ρКТ dt

где V _под — объём газовой полости демпфера.

На основании второго закона Ньютона запишем уравнение для компонента топлива в переливной магистрали, соединяющей демпфер и РМ. Ввиду незначительной, по сравнению с РМ, длиной магистрали, соединяющей полость демпфера с РМ, пренебрежём инерционностью столба КТ в данной магистрали, и запишем уравнение количества движения следующим образом:

вх.дв демпф sg демпф ^ζ пер.маг

G ² демпф

² ρ КТ ^S п ² ер.маг

где  Pдемпф  — давление газа надду ва в газовой полости демпфера; ζ пер.маг и Sпер.маг — коэффициент гидравлического

где R — газовая постоянная газа наддува; Т — среднемассовая температура в подушке демпфера; G _надд — расход наддува демпфера; G _др — расход газа через дренажную магистраль демпфера.

После проведения дифференцирования левой части, а также с учётом формул (1)–(9), получим следующее выражение:

dVпод =   1   × dt P демпф

× ( G – G ) RT – V   ^{dP демпф} ,       (10)

надд др           под _dt

где

dP демпф

dt

производная давления

в подушке демпфера по времени работы ДУ.

Расход дренажа демпфера определя-

ется в зависимости от положения поверхности КТ в демпфере (уровень отсчитывается от среза дренажа демпфера):

• при положении уровня КТ h в демпфере выше среза дренажа демпфера (и выше критического уровня КТ над уровнем среза дренажа демпфера) из демпфера осуществляется расход КТ; расход газа из подушки демпфера не осуществляется; расход КТ через дренажную магистраль рассчитывается по следующей зависимости [7, 8]:

G

КТ

S _др

_ζ        ^{2( P} демпф ^{– P} атм^{) ρ} КТ^{,      (11)}

др.маг

где S _др — площадь проходного сечения жиклёра дренажа; ζ _др.маг — коэффициент сопротивления дренажной магистрали, приведённый к диаметру жиклёра; P _атм — давление на выходном срезе магистрали дренажа демпфера; ρ _КТ — плотность КТ.

• при положении уровня КТ h в демпфере ниже среза дренажа демпфера из подушки демпфера осуществляется расход газа, который рассчитывается по следующей зависимости:

G _КТ = π D ρ _КТ h ^1,5 gn_x .                   (14)

При течении ГЖС через дренаж демпфера расчёт её газосодержания осуществляется по следующим зависимостям:

G др

^S др

_ζ        ^{2( P} демпф ^{– P} атм^{) ρ} g ^{,        (12)}

^ζ др.маг

^Q ГЖС

S др

демпф атм

^ζ др.маг     ρ КТ

;

– ϕ) + ρ _g ϕ

где ρ _g — средняя плотность газовой среды в магистрали дренажа демпфера;

• при положении уровня КТ h выше среза дренажа демпфера, но ниже критического уровня КТ относительно среза дренажа демпфера осуществляется забор из демпфера ГЖС (газа из подушки и КТ из демпфера); расход жидкости в этом случае определяется уровнем КТ над срезом дренажа демпфера, суммарный расход ГЖС определяется пропускной способностью магистрали дренажа демпфера. Критический уровень жидкости — уровень, при котором образуется воронка и начинается прорыв ГЖС в дренажную магистраль демпфера (рис. 3).

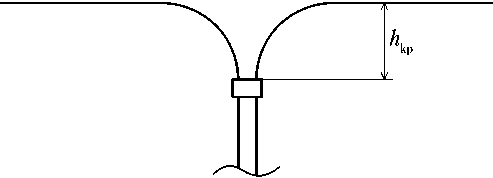
Рис. 3. Критическая высота положения зеркала компонента топлива относительно среза дренажной магистрали демпфера (рисунок создан автором)

Критический уровень КТ относительно дренажа демпфера в первом приближении определяется как для водослива с широким порогом:

h кр

G       2/3

кр

π D ρ _КТ gn_x

где G _кр — расход жидкости через дренаж демпфера при условии отсутствия газа в сбрасываемом КТ при текущем давлении в подушке демпфера; D — диаметр жиклёра дренажа демпфера.

Расход КТ при уровне КТ h над срезом дренажа демпфера между критическим и нулевым (т. е. на уровне среза дренажа демпфера) осуществляется по следующей зависимости [9, 10]:

^Q ГЖС

Q _КТ

Q _КТ

1 – ϕ ^;

G

КТ

^, ρ _КТ

где ρ _g — средняя плотность газа в составе ГЖС; ϕ — среднее по длине магистрали дренажа объёмное газо-содержание газовой смеси (при отсутствии скольжения фаз); Q _КТ — объёмный расход КТ; G _КТ — массовый расход КТ.

После преобразования указанных исходных зависимостей (11)–(17) получим следующие расчётные формулы [9, 11]:

AA =	2 S д 2 р( P демпф –	P атм) ρ К 2 Т	(18)
	ζ др.	; маг
BB =	– G КТ (ρ КТ –	ρ g );	(19)
CC =	– G К 2 Т ρ g ;		(20)

DD = 2 BB – 4 AA∙CC ;

ϕ _КТ

– BB +

;

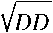
2 AA

ϕ = 1 – ϕ _КТ ,

где величины АА , ВВ , СС , DD являются промежуточными расчётными величинами и по сути представляют собой расчётные коэффициенты получившегося квадратного уравнения.

Расход газа в составе смеси рассчитывается по следующей формуле:

G

ГЖС

S др

×

^ζ др.маг

× 2( P демпф – P атм )[ρ КТ (1 – ϕ) + ρ g ϕ];      (24)

G др = G ГЖС

где G _др , G _КТ , G _ГЖС — расходы газа, КТ в составе смеси и суммарный расход смеси соответственно.

Решая уравнения (18)–(25), найдём зависимости для параметров в газовой полости демпфера.

Данные зависимости позволят получить замкнутую систему уравнений для решения задачи и привести ее к каноническому виду.

с

КТ,

Расчёт объёмной жёсткости демпфера проводится по следующей зависимости:

∏ = k PVдемпф, (26) под где k — показатель адиабаты, для гелия k = 1,66; Vпод — объём газовой полости демпфера.

Полученная система дифференциальных уравнений может быть записана в замкнутом виде А { X } = f ({ X }, t ):

H РМ	0	0	0		dG РМ / dt		F
1	1	0	0	×	dG   / dt демпф	=	0	,          (27)
0	0	ρ КТ	0		dV под / dt		–G демпф
0	0	P демпф	V демпф		dP / dt демпф		Q

где F = демпф sgn демпф

ζ G ²

пер.маг демпф

^{2 ρ} КТ ^S п ² ер.маг

^{2 S} РМ

местн трен

^{2 ρ} КТ ^S пер.маг

G _Р ² _М – ( P _бак + ρ _КТ gn_xH _РМ ) S ² _РМ ;

Q = ( G надд – G др ) RT .

Соответственно, G _др рассчитывается по формулам (11–25). Вектор начальных данных запишется в следующем виде:

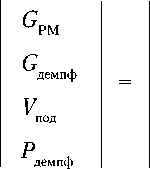
G дв

V под.нач

P бак.нач

.

Начальные правой части

ниже

в

данные, системы разд. 3.2

соответствующие (28), приведены данной работы.

Система уравнений (29) представляет собой каноническую схему записи системы обыкновенных дифференциальных уравнений.

Полученная система дифференциальных уравнений решается численным образом с применением явной схемы Эйлера с шагом интегрирования h_t = 0,014 с. В разд. 3 данной работы приведены результаты расчёта по пяти различным шагам интегрирования, и показана сходимость дан-

Более компактно уравнение (27) можно

записать в

следующем виде:

dG _РМ dt

–F

^H РМ

dG демпф

dt

–F

^H РМ ^;

ного метода к результатам эксперимента. По результатам расчёта получены зависимости объёма газовой полости демпфера, уровня КТ в демпфере относительно среза дренажа демпфера, расхода газа через дренаж демпфера (в т. ч. расхода гелия через дренаж демпфера), расхода КТ через дренаж демпфера.

dV под dt

G демпф

;

ρ _КТ

3. Результаты расчётов и исходные данные

dP демпф dt

V демпф

Q +

демпф демпф

^ρ КТ

.

3.1. Результаты расчётов. По результатам расчётов, выполненных по рассмотренной математической модели, были получены зависимости для основных термодинамических параметров в демпфере, изменения объёмной

жёсткости, уровня КТ в демпфере и газосодержания дренируемого газа. На рис. 4–10 представлены результаты расчётов; на рис. 11 — данные эксперимента, на рис. 12 — расчётное изменение давления в РМ, которое сопоставляется с данными эксперимента, представленными на рис. 11.

Кроме того, проведено сопоставление результатов расчёта процессов в демпфере как с учётом воронко-образования над срезом дренажа демпфера, так и без него. На рис. 8–10 приведено два графика: график, полученный путём расчёта поставленной задачи в рамках предложенной модели с учётом воронкообразования над срезом дренажной магистрали демпфера, и график без учёта воронко-образования.

На рис. 4 график изменения давления на входе в МД, начиная с определённого момента, представлен широкой полосой, которая при более детальном рассмотрении представляет собой осциллирующий процесс, вызванный колебаниями топлива в системе.

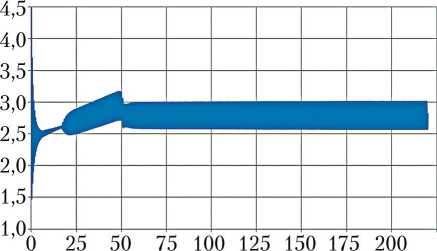
Рис. 4. Изменение давления на входе в маршевый двигатель (рисунок создан автором)

На рис. 5 представлено положение поверхности КТ относительно критической высоты. Как можно видеть, большую часть времени поверхность КТ находится ниже критической высоты, где существенную роль играет воронкообразование, рассмотренное в работе. То есть дренируется в основном ГЖС.

Как можно видеть на рис. 6, колебания КТ в РМ находятся в узких диапазонах и в целом разброс не выходит за рамки допустимых границ (в пределах 7% от номинального значения, представленного в исходных данных в разд. 3.2 статьи).

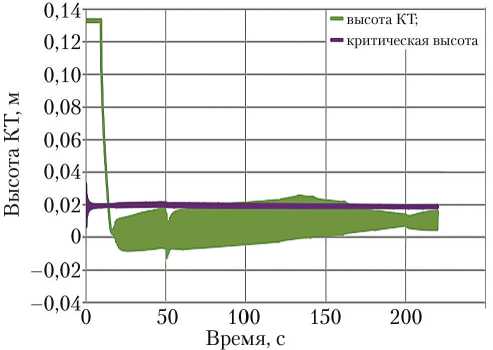
Рис. 5. Положение поверхности компонента топлива (КТ) относительно критической высоты ( рисунок создан автором)

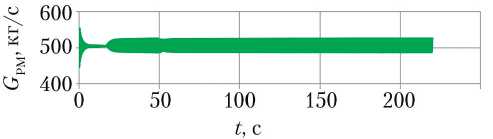
Рис. 6. Изменение расхода компонентов топлива в расходной магистрали (рисунок создан автором)

Как можно видеть на рис. 7, изменение объёмного газосодержания носит колебательный характер, что обуслов-

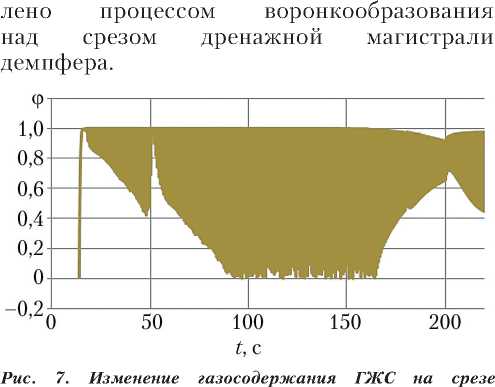
дренажной магистрали (рисунок создан автором)

Как можно видеть на рис. 8, объёмная жёсткость демпфера уже через 10 с после выхода МД на режим оказывается ниже заданного уровня (который задаётся для систем с похожими характеристиками на уровне 1,4). Кроме того, учёт воронкообразования над срезом дренажной магистрали демпфера практически не влияет на объёмную жёсткость. Далее рассмотрим влияние учёта воронкобразования над срезом дренажной магистрали демпфера на общую картину процесса.

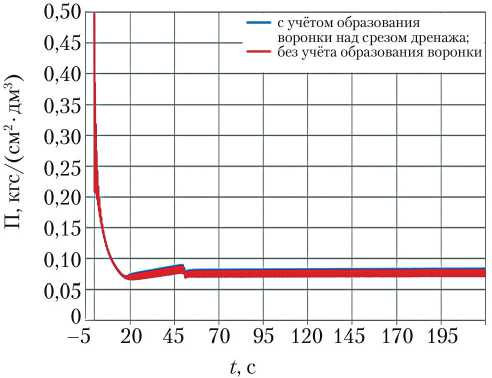
Рис. 8. Изменение объёмной жёсткости демпфера (рисунок создан автором)

Как можно видеть на рис. 11, осред-нённая частота колебаний также составляет ~2 Гц.

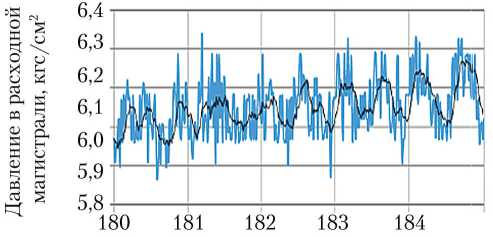
t, с

Рис. 11. Изменение давления в расходной магистрали в ходе лётно-конструкторских испытаний первой ступени ракеты-носителя со сходными характеристиками: ^— — данные датчиков в ходе эксперимента; ^— — линия тренда (рисунок создан автором)

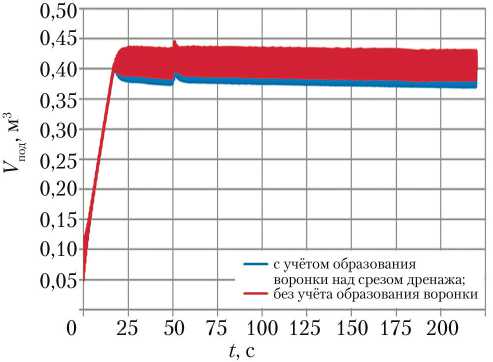
Рис. 9. Изменение объёма газовой полости демпфера (рисунок создан автором)

На рис. 12 представлены данные, аналогичные данным на рис. 4 в узком временном диапазоне 185…188 с.

Как можно видеть, расчётные данные на рис. 12 практически совпадают с экспериментальными данными на рис. 11. Колебательные процессы совпадают по среднему значению (относительно которого происходят колебания), амплитуде и частоте. Таким образом, учёт воронкообразования, рассмотренный в данной работе, является существенным.

Как можно видеть на рис. 10, учёт воронкообразования, рассмотренный в работе, очень существенно влияет на частоту колебаний в системе. Так, при учёте воронкообразования частота колебаний составляет ~2 Гц, без учёта — ~1 Гц.

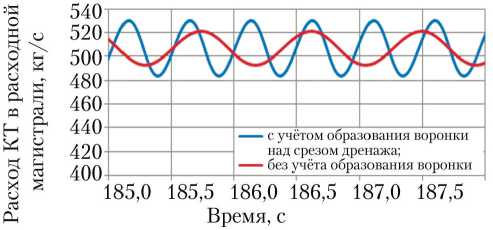
Рис. 10. Изменение расхода компонента топлива (КТ) в расходной магистрали со 185 по 188 с (рисунок создан автором)

На рис. 11 представлены данные по изменению давления в РМ, полученные в ходе эксперимента.

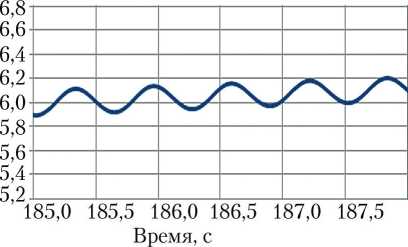
Рис. 12. Изменение давления в расходной магистрали, полученное в процессе расчёта по представленной в работе математической модели (рисунок создан автором)

Рассмотренная в работе математическая модель даёт хорошее совпадение с экспериментальными данными. Учёт воронкообразования является важной частью модели, без учёта которого модель даёт значительно менее корректные результаты. Ниже, в разд. 3.3 данной работы, будут рассмотрены вопросы сходимости численного метода, применяемого для расчёта.

• 3.2.    Исходные данные для расчёта. Исходные данные приближены к параметрам реального изделия, однако не совпадают с ними.

Исходные данные для расчёта:

начальное время расчёта	0 с;
конечное время расчёта	220 с;
температура подушки демпфера	80 К;
давление паров насыщения	0,15 кгс/см 2 ;
плотность КТ	1 148 кг/м 3 ;
температура КТ	80 К;
начальное давление на входе в двигатель	5,5 кгс/см 2 ;
начальное давление в подушке демпфера	3,5 кгс/см 2 ;
диаметр жиклёра демпфера	4 мм;
радиус сферы демпфера	0,233 м;
высота дренажной магистрали	0,1 м;
газовая постоянная гелия	2 077;
газовая постоянная паров кислорода	260;
ускорение свободного падения	9,8 м/с 2 ;
атмосферное давление	1 кгс/см 2 ;
коэффициент адиабаты гелия	1,66;
коэффициент гидравлического сопротивления дренажной магистрали демпфера	1,5;
коэффициент гидравлического сопротивления соединительной магистрали между демпфером и расходной магистралью	1,5;
диаметр жиклёра дренажной магистрали	1 мм;
начальное давление в шаробаллонах (ШБ)	220 кгс/см 2 ;
начальная температура в ШБ	90 К;
объём ШБ наддува демпфера	25 дм 3 ;
начальный объём газовой полости демпфера	0,005 м 3 ;
расход КТ через двигатель	507 кг/с.

В качестве исходных данных в мо- дель закладывается изменение давления в газовой полости бака на режиме работы МД рассматриваемой ступени. Это может быть как результат расчёта по математической модели, так и аппроксимация результатов лётноконструкторских испытаний. В данной работе рассматривалось достаточно грубое приближение, приведённое на рис. 13.

Конечное время расчёта Т _кон = 220 c берётся с небольшим запасом относительно времени работы МД ступени РН.

На рис. 14 представлены данные по перегрузке, заложенные в расчёт.

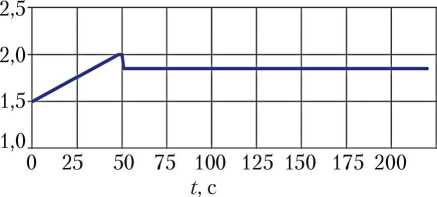
Рис. 13. Давление в газовой полости топливного бака (рисунок создан автором)

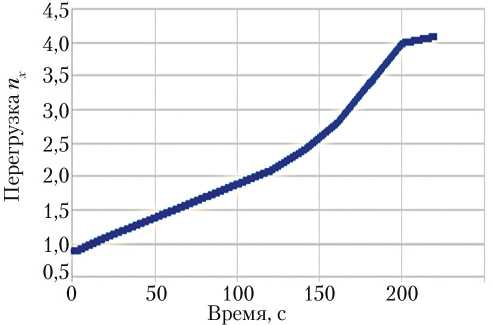
Рис. 14. Изменение перегрузки, заложенное в расчёт (рисунок создан автором)

• 3.3.    Оценка сходимости численного метода. Для оценки сходимости рассматриваемой в работе разностной схемы на основе явной схемы Эйлера рассмотрим изменение объёма газовой полости демпфера, которое было получено в результате численного интегрирования уравнений. Численное интегрирование системы уравнений было выполнено при пяти различных шагах интегрирования, каждый из которых получался путём деления предыдущего шага на два. Далее проводилась оценка изменения поведения данного параметра при каждом последующем шаге интегрирования. Результаты данной оценки представлены в табл. 1, 2. В левой колонке приведены графики изменения параметра по всей циклограмме полёта, в правой — в интервале 50…55 с согласно циклограмме полёта, N_t — число делений расчётного интервала по времени, h_t — шаг интегрирования по времени. По графикам приведенным в табл. 1, 2 видно, что представленная расчётная схема сходится.

Таблица 1

Изменение объёма газовой полости демпфера V _под (рисунки созданы автором)

Nt = 4000, ht = 0,055 0,050 т------------г------------1------------1------------1------------ 0,045 —?---U~-~-J-~~~-J----,--- 0,040                                     I ---- „ 0,035-                          — S 0,030----- g 0,025 f----- ^= 0,020f/----- 0,0151----- 0,0101/----- 0,05 V ---- 0       50     100    150    200 t, c	Nt = 4000, ht = 0,055 0,047 1---------------------------------------- 0,045-- Д---- 5: V WW\, 0,039 V----~ 0,037------ 0,035 50    51     52     53     54     55 t, c
Nt = 8000, ht = 0,028 0,050 j------------1------------1------------1------------T------------ 0,045 — ......ЦJJ ,_ --- 0,040                        — „ 0,035-                                      ---- S 0,030 /----- g 0,025 1----- ^= 0,020(7------------------------------------ 0,0151----- 0,010 /----- 0,05 V  ^^ ^^ ^^ ^^ 0       50     100    150    200 t, c	Nt = 8000, ht = 0,028 0,047 1---------------------------------------- 0,045------ ^ 0,043------ s 0,041 0,039------—3 0,037------ 0,035 50     51      52     53     54     55 t, c
Nt = 16000, ht = 0,014 0,045              i          ।           ।                ------ 0,040 --<^Z2ZZZ_ZZZ^— 0,035 - 1-- ~ 0,030----- ^ 0,025 f----- Л 0,020(7----- 0,0151----- 0,010 f----- 0,05 у ---- 0       50     100    150    200 t, c	Nt = 16000, ht = 0,014 0,047 1---------------------------------------- 0,045------ ^ 0,043------ s 0,041 0,039------—3 0,037------ 0,035 50     51      52     53     54     55 t, c
Nt = 32000, ht = 0,007 0,045               i           ।            ।            i ------- 0,040 --<^Z2ZZZ_ZZZ^— 0,035 - 1-- ~ 0,030-f----- ^ 0,025 f----- Л 0,020(7----- 0,0151----- 0,010 f----- 0,05 у ---- 0       50     100    150    200 t, c	Nt = 32000, ht = 0,007 0,047 1---------------------------------------- 0,045------ ^ 0,043------ s 0,041 0,039------—3 0,037------ 0,035 50     51      52     53     54     55 t, c
Nt = 64000, ht = 0,003 0,045               i           ।            ।            i ------- 0,040 --<^Z2ZZZ_ZZZ^— 0,035 - 1-- ~ 0,030-f----- ^ 0,025 f----- Л 0,020(7----- 0,0151----- 0,010 f----- 0,05 у ---- 0       50     100    150    200 t, c	Nt = 64000, ht = 0,003 0,047 1---------------------------------------- 0,045------ ^ 0,043------ s 0,041 0,039------—3 0,037------ 0,035 50     51      52     53     54     55 t, c

Из графиков, приведённых в табл. 1, видно, что:

• •    изменение объёма газовой полости демпфера носит осциллирующий (колебательный) характер;

• •    период колебаний практически не зависит от шага интегрирования, а вот амплитуда и, в меньшей степени, фаза несколько различаются;

• •    при уменьшении шага интегрирования колебательный процесс уже практически не меняется ни по периоду, ни по фазе, ни по амплитуде;

• •    при расчёте с шагом интегрирования h_t = 0,014 с график колебательного процесса меняется слабо.

На приведённых графиках видно наличие сходимости.

Для количественной оценки сходимости рассмотрим изменение пикового значения объёма газовой полости демпфера в период 53…54 с согласно циклограмме полёта. Пиковое значение присутствует на всех графиках. В табл. 2 приведены «пиковые» значения рассматриваемого параметра на данном интервале при уменьшении шага интегрирования.

Из табл. 2 видно, что невязка, отражённая в третьем столбце, уменьшается при уменьшении шага интегрирования, что говорит о сходимости рассматриваемой разностной схемы.

Изменение «пикового» значения объёма газовой полости демпфера в период с 53 по 54 с по циклограмме полёта

Таблица 2

Номер шага	Шаг интегрирования по времени, с	Максимальное значение объёма газовой полости демпфера между 53 и 54 с	Разница между максимальным значением объёма газовой полости в интервале 53…54 с при данном шаге интегрирования по времени и при предыдущем шаге
1.	ht 1 = 0,110	0,0495749	–
2.	ht 2 = 0,055	0,0451847	0,00439
3.	ht 3 = 0,028	0,0435128	0,00167
4.	ht 4 = 0,014	0,0424815	0,00103
5.	ht 5 = 0,007	0,0422533	0,00023
6.	ht 6 = 0,003	0,0421780	0,00008

Выводы

• 1.    Рассмотренная в работе модель даёт в целом хорошее совпадение с результатами эксперимента.

• 2.    Существенным элементом предложенной в работе модели является учёт воронкообразования над срезом дренажа демпфера. Без учёта воронко-образования модель даёт значительно менее корректные результаты.

• 3.    В системе возникают автоколебания, однако они не выводят параметры пневмогидравлической системы подачи топлива за рамки допустимых диапазонов.

• 4.    Предложенная модель даёт в целом корректный, с точки зрения разумных допусков, разброс значений расходов КТ в топливной магистрали, не выходящий за требования стандартных технических условий на двигатели (в пределах 5–7%), а также выдаёт частоту колебаний параметров на уровне

~2 Гц, что соответствует данным лётноконструкторских испытаний изделий со сходными параметрами.