Моделирование прогнозных значений вероятностей состояний систем с использованием цепей Маркова

Теория вероятностей получила свое развитие из убеждения, что в массовых случайных событиях могут проявляться закономерности. Современная теория вероятностей изучает случайные процессы, для которых знания предыдущего опыта влияет на предсказания результатов будущих экспериментов. [1,5] А именно, когда наблюдателю необходимо провести последовательность случайных экспериментов, все предшествующие результаты могут повлиять на прогнозирование итогов последующего эксперимента. Например, предсказание оценки учащегося на экзамене по последовательности полученных им оценок в процессе изучения курса. Однако случайные процессы могут допускать такую общность, что сложно доказать общие результаты.

В 1907 году Андрей Андреевич Марков начал изучение такого важного понятия в теории вероятности, как процесс. Под «процессом» понимается последовательность случайных событий, в которой исход предыдущего события может повлиять на результат следующего события. [6,7] Такой тип процесса был назван цепью Маркова. Марковские цепи являются довольно распространенным и относительно простым способом статистического моделирования случайных процессов. Они используются в самых разных областях, от генерации текста до финансового моделирования.

В качестве примера с использованием цепи Маркова можно привести модель прогнозирования погоды. Как правило, погода может находиться в двух возможных состояниях: солнечная погода или пасмурная. Можно непосредственно наблюдать текущее состояние погоды. При этом гарантировано, что оно всегда будет одним из двух вышеупомянутых состояний. Предположим, что необходимо предсказать погоду на следующий день. В этом процессе есть неотъемлемый переход, поскольку текущая погода влияет на погоду следующего дня. Таким образом, для достижения цели осуществляется сбор данных о погоде в течение нескольких лет и подсчитывается, что вероятность солнечного дня, следующего после пасмурного, составляет 0,25. Так как у погоды существует только два возможных состояния, то вероятность пасмурного дня после пасмурного должна быть 0,75. Теперь можно использовать полученную дистрибуцию для прогноза погоды на ближайшие дни, основываясь на текущем состоянии погоды в заданное время.

Рисунок 1. Визуализация примера погоды

Распределение вероятности получается только путем наблюдения переходов с текущего дня на следующий и никак не зависит от погоды предшествующих дней. Этот пример иллюстрирует свойство Маркова, которым и характеризуются Марковские процессы. Цепь Маркова по существу состоит из набора переходов, которые определяются некоторым вероятностным распределением, удовлетворяющим Марковскому свойству. Так как выводы делаются на основе реальных наблюдений, то, как правило, цепь Маркова не позволяет успешно создавать последовательности, в которых ожидается определенная общая тенденция. Например, в то время как цепь Маркова может имитировать стиль письма автора, основанный на частоте слов, она не сможет создать текст, который содержит глубокий смысл или тематическое значение, поскольку они разработаны на гораздо более длинных последовательностях текста. [3] Поэтому с помощью Марковских цепей нет возможности создавать контекстно-зависимый контент, поскольку они не могут принимать во внимание полную цепочку предшествующих состояний.

Цепь Маркова можно описать следующим образом: имеем множество состояний, 5 = {s₁,s₂,...,s_r}. Процесс начинается в одном из этих состояний и последовательно перемещается из одного состояния в другой. Каждое движение называется шагом. Если цепочка в настоящее время находится в состоянии s , , тогда он переходит на состояние S j на следующем шаге с вероятностью, обозначенной р^-, и это вероятность не зависит от того, в каких состояниях цепь находилась перед текущим состоянием.

Вероятности р^ называются вероятностями перехода. Процесс может остаться в состоянии, в котором он находится, и это происходит с вероятностью рц .[5,6] Начальная вероятность распределение, определенное на S, определяет начальное состояние. Обычно указывают конкретное состояние как начальное состояние.

В моменты времени t 1 , t₂, t₃ проводится осмотр ЭВМ. Возможны следующие состояния ЭВМ:

• S₀    — полностью исправна;

• S 1    — незначительные неисправности, которые позволяют эксплуатировать ЭВМ;

S2 — существенные неисправности, дающие возможность решать ограниченное число задач;

S 3 — ЭВМ полностью вышла из строя.

Пусть матрица переходных вероятностей имеет вид:

НМ =

1 0,5  0,3

0   0,4

0,2 0,4 0,3

0 0,2 0,7 1

Необходимо построить граф состояний. Найти вероятности состояний ЭВМ после одного, двух, трех осмотров, если вначале (при t = 0) ЭВМ была полностью исправна.

Решение:

Построим граф состояний:

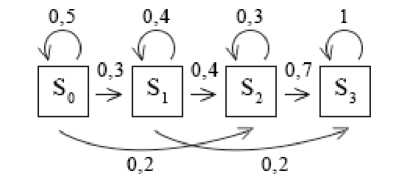
По условию вектор вероятности состояний ЭВМ в начальный момент времени (до первого осмотра) равен:

р(0) = (1;0; 0; 0)

После первого осмотра:

Р0(1) = Р0(0^ * Р00 = 1 * 0,5 = 0,5 — полностью исправна;

Р 1 (1) = Р 0 (0) * Р₀₁ = 1 * 0,3 = 0,3 — незначительные неисправности, которые позволяют эксплуатировать ЭВМ;

Р2(1) = Р0(0) * Р02 = 1 * 0,2 = 0,2  — существенные неисправности,

дающие возможность решать ограниченное число задач;

Р₃(1) = Р 0 (0) * Р₀₃ = 1*0 = 0 — ЭВМ полностью вышла из строя.

После второго осмотра:

Р0(2) = Р0(1) * Р00 = 0,5 * 0,5 = 0,25 — полностью исправна;

Р1(2) = Р0(1) * Р01 + Р1(1) * Рп = 0,5 * 0,3 + 0,3 * 0,4 = 0,27       —

незначительные неисправности, которые позволяют эксплуатировать ЭВМ;

Р 2 (2) = Р о (1) * Р 02 + Р 1 (1) * Р 12 + Р₂(1) * Р 22 = 0,5 * 0,2 + 0,3 * 0,4 + 0,2 * 0,3 =0,28 — существенные неисправности, дающие возможность решать ограниченное число задач;

Р3(2) = Р2(1) * Р23 + Р1(1) * Р13 = 0,2 * 0,7 + 0,3 * 0,2 = 0,20 — ЭВМ полностью вышла из строя.

После третьего осмотра:

Р0(3) = Р0(2) * Р00 = 0,25 * 0,5 = 0,125 — полностью исправна;

Р1(3) = Р0(2) * Р01 + Р1(2) * Р11 = 0,25 * 0,3 + 0,27 * 0,4 = 0,183    —

незначительные неисправности, которые позволяют эксплуатировать ЭВМ;

Р2(3) = Ро(2) * Р02 + Р1(2) * Р12 + Р2(2) * Р22 = 0,25 * 0,2 + 0,27 * 0,4 + 0,28 * 0,3 = 0,242  — существенные неисправности, дающие

возможность решать ограниченное число задач;

Рз(3) = Р1(2) * Р1з + Р2(2) * Р23 + Рз(2) * Рзз = 0,27 * 0,2 + 0,28 * 0,7 + 0,20 * 1 = 0,450 — ЭВМ полностью вышла из строя.

Процесс моделирования демонстрируется на рисунками 2 и 3.

	А	В	С	С	Е	F	G	н
1	Матрица переходных вероятностей имеет вид:
2
3		0,5	0,3	0,2	0
4 5	Р|	0	0,4	0,4	0,2
		0	0	0,3	0,7
6		0	0	0	1

9	1 осмотр:			II осмотр:			III осмотр:
10	Poll)	=гвз		Ро(2)	=В10*ВЗ		Ро(3)	=Е10*ВЗ
11	Р1(1)	=1*СЗ		Р1И	=В10*СЗ+В11*С4		PJ3)	=Е1О*СЗ+Е11*С4
12	р,(1)	=1*03		PJ2)	=B1O*D3+B11*C4+B1		PJ3)	=E1O*D3+E11*D4+E1
13	Рз(1)	=ГЕЗ		Рз(2)	=В12*Е5+В11*Е4		Р3Р)	=Е11*Е4+Е12*Е5+Е13

Рисунок 2. Режим формул

и	А	в	С	0	Е	Е		Н J
1	Матрица переходных вероятностей имеет вид:
2
3		0,5	0,3	0,2	0
4	PS	0	0,4	0,4	0,2
5		0	0	0,3	0,7
5		0	0	0	1
7
8
9	1 осмотр:			II осмотр:			III осмотр:
10	Poll)	0,5		з:<2;	0,25		Ро(3)	0,125
11	Pi(l)	0,3		Pi(2)	0,27		PJ3)	0,183
12	Р=(1)	0,2		Pz(2)	0,28		Рг(3)	0,242
13	Рз(1)	0		РЭ(2)	0,2		Р3(3)	0,45

Рисунок 3. Режим результатов расчетов