Моделирование прохождения ИК-излучения через алмазную дифракционную линзу с субволновыми технологическими погрешностями микрорельефа

Использование в промышленности мощных СО₂-лазеров ( Х =10,6 мкм) обуславливает интерес к алмазным дифракционным элементам, предназначенным для фокусировки лазерного излучения в области различной конфигурации. В частности, в [1-3] исследовались дифракционные оптические элементы (ДОЭ) - фокусаторы и линзы, изготовленные прямым лазерным травлением поверхности алмазной пленки ( n =2,4) путем селективной абляции с помощью эксимерного УФ-лазера.

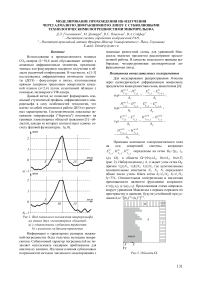
Данный метод не позволяет формировать идеальный ступенчатый профиль дифракционного микрорельефа в силу особенностей технологии, что влечет за собой отклонения в работе ДОЭ от расчетных характеристик. Систематические локальные искажения микрорельефа ("бортики") возникают на границах элементарных областей травления [3] - областей, каждая из которых соответствует одному отсчету фазовой функции (рис. 1а, б).

помощью разностной схемы для уравнений Максвелла является предметом рассмотрения предложенной работы. В качестве модельного примера выбиралась четырехуровневая цилиндрическая дифракционная линза.

Постановка вычислительных экспериментов

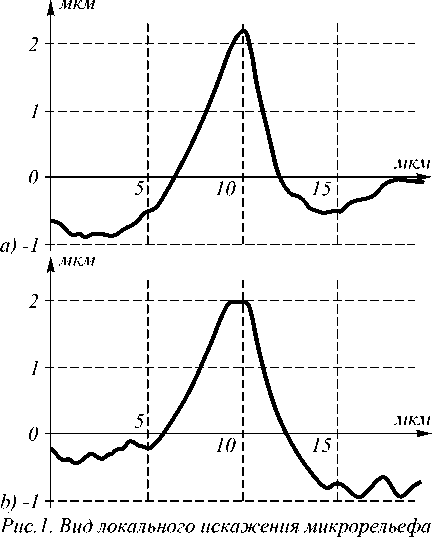
Для моделирования распространения Н -волны через цилиндрическую дифракционную микролинзу предлагается явная разностная схема, аналогичная [4]:

№

Нп+1 - Hn     En - En yj, k        yj, k           xj, k       xj, k-1 .

-----------------=--.

ht                  hz

№

H^{n + 1} z j, k

Hn

z j, k

Eⁿ - Eⁿ x j , k       x j - 1, k

ht

hy

E n + 1 E n j n + 1    j n + 1

xj, k       xj, k = zj+1, k       zj, k ht                hy

на стыке двух элементарных областей: а) с одинаковыми глубинами травления; b) с разными глубинами травления.

на

jj n + 1      jj n + 1

y j , k + 1        y j , k

. h _z

Проекции компонент электромагнитного поля оси декартовой системы координат

Eⁿ x j , k

, Hn , Hn   определены на сетке Qh={(yj, zk, yj, k     zj, k

t _n ) e Q }, в области Q ={0 < y < L y , 0 < z < L _z , 0 < t < 7 } (рис. 2). Набор индексов j, k, n задает узлы сетки Q h , причем 1 < j < N _y , 1 < k < N _z , 1 < t < N _t , где целочисленные положительные константы N _y , N _z , N _t определяют общее число узлов. Шаги сетки h _y = L _yI N _y , h _z = L _zI N _z , h _t = T । N _t . Относительная электрическая и магнитная проницаемости являются функциями координат:

Информация о характерных размерах искаже-ний-погрешностях была получена методами микроскопии. Субволновый характер погрешностей не позволяет использовать скалярное приближение для анализа их влияния. Изучение влияния субволновых погрешностей методом численного моделирования с

s = s ( y j ,z _k ), p = p ( y j ,z _k ). Предложенная схема аппроксимирует уравнения Максвелла с первым порядком по

Особое внимание при записи схемы уделялось постановке граничных условий. Область моделирования ( А ) с трех сторон ограничивалась совершенно поглощающим слоем [5] ( B, C, D ), необходимым для имитации вакуума вокруг области А . Основная идея

метода совершенно поглощающего слоя состоит в введении в уравнения Максвелла наряду с электри

ческой проводимостью среды ( a y , a z ) фиктивной магнитной проводимости ( a y , a z ) таким образом, чтобы импеданс среды соответствовал импедансу вакуума a / s o = a / ц о -

Тогда в области В схема запишется как:

Н П + = exp^ h / Ц о H" + z j , k                       j ' z j , k

*

(1 - exp(-ayh I цо))

+-—.—-x          (1)

^a z k h y

xf En   + En - En - En    ),

( xy j , k       xz j , k       xy j - 1, k       xz j - 1, k )

Ц 0Ц

Hl+1 - HH yj, k       yj, k ht

f En + En  WEn   + En 1

( xy j , k       xz j , k ) ( xy j , k - 1       xz j , k - 1 )

hz

£о£

En+1 - En xyj, k      xyj, k ht

^H^n + 1     ^H^ + 1

y j , k + 1 ~ y₇ , k h_z

E; k = exp ( - ° y j h_t I S o EE¹ + ^{( 1 -} eps ^(- a h I ^£ о ) n + 1 ⁺--- H^ "  ° y j y

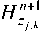
В области C схема принимает вид:

H n ^{n +} 1 = exp ⁽- a*_z h t / ц о V - y j , k           ^{x k}                 y j , k

(,

1- exp(-aA / ц о))-             kx

a* hz zk z

x

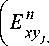
+ En xzj, k

En xyj, k-1

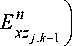
ЦоЦ

H r + 1 ^z j , k

-

Hn

z j , k

ht

Eⁿ xy jk

+ En xzj, k

En xyj-1,k

+ En xzj-1,k

hy

En+1 = exp(- a h, / s0 )En+1 - xyj k      p\    zk t о /ХУ

(1 - eps l-a7 ht / £ ))

z k t ^о f П + 1           П + 1 I

--H - H , a, h7 I yj,k+1      yj,k)

^z k ^z

E^n + 1   En      H^ + 1   H^ + 1

xzj, k      xzj, k =    zj+1, k       zj, k ht                hy

И в области D схема состоит из уравнений (1);

(2); (3); (4).

В свою очередь области B, C и D граничат с электрической стенкой, которой соответствуют условия первого рода (для тангенциальной проекции электрического и нормальной проекции магнитного поля) и условия второго рода (для нормальной проекции электрического и тангенциальной проекции магнитного поля).

Прямой z = L _z (главной оптической оси линзы) соответствует магнитная стенка, задающая условия первого рода для H z и условия второго рода для E x и H y . Такое представление граничных условий позволяет рассматривать половину дифракционной линзы, учитывая ее симметричность относительно главной оптической оси.

На прямой z =О задаются условия первого рода, соответствующие распространяющейся в линзе электромагнитной волне.

Были поставлены три серии вычислительных экспериментов, в которых исследовалась четырехуровневая дифракционная линза с фокусным расстоянием У =4,5 мм и апертурой L y x 2=1 мм. Каждой серии экспериментов соответствовала линза с линейным размером элементарной области травления s =3О мкм, s =4О мкм и s =6О мкм. Протяженность области Q по координате Z и время постановки эксперимента выбирались так, чтобы отразившаяся от дифракционного рельефа волна не успела дойти до прямой y =О, а через линзу прошел цуг длиной не менее 5 Х . Тогда L z =1О6 мкм и T =7,12813 х 1О^-13 с. Предполагалось, что линза освещается нормально падающим гауссовым пучком с радиусом перетяжки w =3О Х .

a)

b)

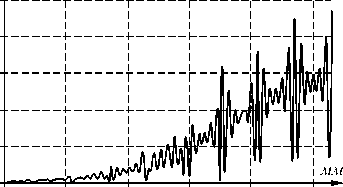
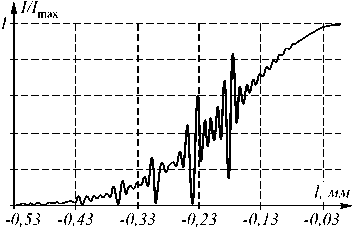
Рис. 3. Распределения интенсивности I = | E ?|

в плоскости за линзой при s=60 мкм a) без локальных искажений микрорельефа, b) с искажениями.

Целью первого эксперимента каждой серии было получение распределения комплексной амплитуды волны E [6] в плоскости за линзой без ло-

кальных искажений микрорельефа, второго эксперимента - с искажениями (рис. 3).

Осцилляции интенсивности на рис. 3а вызваны ступенчатым характером расчетного микрорельефа. Локальные технологические искажения микрорельефа приводят к увеличению частоты осцилляций (рис. 3b). Впоследствии с помощью интеграла Кирхгофа [7] рассчитывались распределения интенсивности в фокальных плоскостях линз (рис. 4).

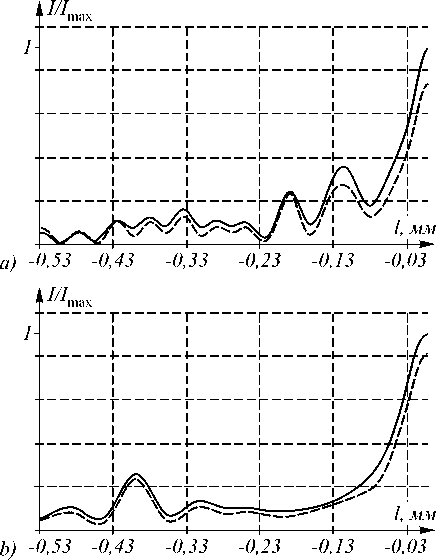
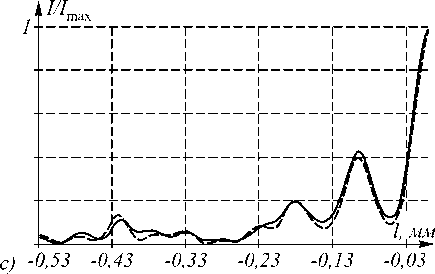
Рис. 4. Распределения интенсивности

I = E

в фокальной плоскости для линз с линейным размером элементарной области травления a) s=30 мкм, b) s=40 мкм, c) s=60 мкм.

Черная кривая соответствует линзе без искажений, пунктирная - с искажениями.

Анализ результатов

Условимся под эффективностью линзы с локальными искажениями микрорельефа e € понимать отношение энергии, попавшей в центральный максимум в фокальной плоскости такой линзы, к энергии, попавшей в центральный максимум в фокальной плоскости линзы без искажений.

Как видно из анализа (рис. 4), эффективность линзы с локальными искажениями микрорельефа возрастает при увеличении линейного размера элементарной области травления s. Так, если для линзы с s =30 мкм e €=0,78, то для линзы с s =40 мкм - e €=0,81, а для линзы с s =60 мкм - e €=0,91. Это связано с уменьшением доли непроработанных областей в общей площади линзы. Отметим, однако, что увеличение размера элементарной области травления ведет к снижению точности аппроксимации расчетной непрерывной фазовой функции линзы ее дискретным аналогом [8].